Fundamentos da Lógica

Introdução a lógica proposicional

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Iniciamos agora nossa introdução à lógica proposicional. Esse conhecimento o capacitará a construir condições lógicas embasadas em regras e a valorar o resultado dessa condição. Sem dúvida, esse conhecimento é imprescindível na construção de algoritmos computacionais.
Imagine que você está concorrendo a uma vaga de desenvolvedor de software em uma empresa e precisa criar um programa que permita aos funcionários acessar áreas específicas com base em suas permissões. O sistema deve ser capaz de tomar decisões lógicas para permitir ou negar o acesso com base em premissas específicas.

Premissas:

1. Existem três áreas de acesso na empresa: Sala A, Sala B e Sala C.
2. Existem cinco funcionários: Alice, Bob, Carol, Dave e Eve.
3. Cada funcionário tem um conjunto de permissões que define quais áreas ele pode acessar.

• Alice pode acessar a Sala A.
• Bob pode acessar a Sala A e a Sala B.
• Carol pode acessar a Sala B.
• Dave não tem permissão para acessar nenhuma sala.
• Eve pode acessar a Sala C.

Problema:

Como candidato à vaga de desenvolvedor da empresa, você foi encarregado de implementar um algoritmo que, com base nas premissas citadas anteriormente, determine se um funcionário específico tem permissão para acessar uma determinada área. O algoritmo deve receber o nome de um funcionário e o nome de uma área e retornar uma conclusão lógica sobre se o acesso deve ser permitido ou negado.
Agora é com você! Como você poderá usar as dicas e transformá-las em proposições simples e/ou compostas? Quantas proposições serão necessárias para cada figura geométrica? Quais operadores lógicos você terá que usar para construir as regras? Para vencer esse desafio, nesta seção iremos aprender sobre a lógica proposicional, o que são as proposições simples e como criar as proposições compostas, utilizando os conectivos lógicos de conjunção e disjunção.
Vamos em frente garantir essa vaga de emprego!

Vamos Começar!

Na lógica computacional, vamos utilizar as mesmas regras da Lógica Formal, porém iremos valorar os conteúdos, como verdadeiro ou falso, a fim de extrair nossas conclusões.

Em nosso cotidiano, usamos a linguagem natural para nos expressar por meio de frases, que em alguns casos podem ser argumentativas sendo assim compostas por premissas e conclusões. Vejamos um exemplo extraído de Machado e Cunha (2008, p. 16). Observe o argumento de uma professora sobre o desempenho de um certo aluno: “É lógico que Pedro será aprovado nos exames, pois ele é inteligente e estuda muito e todos os alunos inteligentes e estudiosos são aprovados”. Esse argumento foi construído embasado por premissas (razões) e que levam a uma única conclusão, conforme ilustra o Quadro 1.

Premissas (razões)	1.    Pedro é inteligente. 2.    Pedro estuda muito. 3.    Todos os alunos inteligentes e estudiosos são aprovados.
Conclusão	Pedro será aprovado

Quando 1 | Premissas (razões). Fonte: adaptado de Machado e Cunha (2008, p. 16).

Veja no Quadro 1 que separamos a frase em premissas e conclusão. Nesse caso, três premissas permitiram chegar a uma conclusão coerente. Extrair essa conclusão do argumento só foi possível devido às regras da lógica proposicional, que por meio de premissas e conectores extraem-se resultados lógicos. Fazer essa separação (premissa / conclusão) é muito importante, pois nem toda frase é um argumento. Além disso, imagina que queiramos criar um algoritmo para classificar se um aluno foi aprovado ou reprovado, essas premissas precisam ser programadas em forma de regras, as quais aprenderemos em breve.

Para ser um argumento é preciso existir uma conclusão, logo, nem toda frase é um argumento. Por exemplo, a frase: “Segure firme!”, não possui premissas e conclusões, pois trata-se de uma sentença imperativa (ordem) ou então a frase: “Você pode abrir a porta?” também não é um argumento, pois estamos diante de uma sentença interrogativa. As sentenças exclamativas, como por exemplo, “Que lindo!”, “Parabéns!” também não são consideradas argumentos. No estudo da lógica, além de distinguir se uma frase é ou não um argumento, também é importante distinguirmos se uma sentença pode ou não ser classificada como verdadeira ou falsa (não ambas ao mesmo tempo). Por exemplo, considere as frases:

1. O Brasil é um país da América Latina.
2. Minas Gerais é um estado do Nordeste.
3. São Paulo é a capital do Paraná.
4. Três mais um é igual a quatro.
5. Que horas são?

As quatro primeiras frases podem ser classificadas (valoradas) em verdadeira (V) ou falso (F). Veja:

1. Verdadeira.
2. Falso.
3. Falso.
4. Verdadeira.

Mas a quinta frase não pode ser valorada em V ou F, pois a resposta é um certo horário.

5.?

Essa distinção entre os tipos de sentenças é crucial para o estudo da lógica, pois uma frase que pode ser classificada como verdadeira ou falsa (não ambas ao mesmo tempo) é chamada proposição.

Proposição é uma sentença declarativa que pode ser classificada como verdadeira ou falsa, jamais ambas ao mesmo tempo. Ou seja, não pode haver dúvida quanto à classificação da sentença. Também podemos dizer que se trata de uma classificação binária, pois só existem dois resultados possíveis: V ou F, ou ainda 1 ou 0.

Siga em Frente...

Nem sempre classificar se uma sentença é ou não uma proposição é uma tarefa trivial. Para que seja uma proposição, a sentença declarativa não pode deixar dúvidas quanto ao resultado. Por exemplo, a sentença “Está chovendo agora” não pode ser classificada como V ou F, pois deixa dúvida (por exemplo, pode estar chovendo em um ponto da cidade e em outro não). Para que essa frase se torne uma proposição ela precisa de um contexto, por exemplo, “Está chovendo agora na minha rua”, ou seja, o locutor da frase especificou o local, então agora é possível valorar se o que ele disse é verdadeiro ou falso.

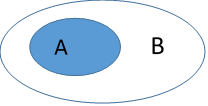
Sabendo que uma proposição é uma sentença declarativa que pode ser classificada como V ou F, podemos encontrá-la nas mais diversas formas. Observe o Quadro 2. Nele temos diagramas de Euler representando conjuntos e sentenças que podem ser classificadas como V ou F, baseado no diagrama, portanto, são proposições.

Diagrama de Euler	Proposição
	Todo A é B
	Nenhum A é B

Podemos utilizar letras maiúsculas do alfabeto para representar as proposições, portanto, a partir de agora adotaremos essa notação para representar as proposições. Por exemplo:

A: Quinze é menor que vinte.

B: Todos os italianos são europeus.

Segundo Bispo e Castanheira (2011), toda proposição deve seguir três princípios básicos:

• Princípio da Identidade: “Toda proposição é idêntica a si mesma”. Ou seja, sendo P uma proposição: P é P.
• Princípio da Não Contradição: “Uma proposição não pode ser verdadeira e falsa ao mesmo tempo”. Sendo P uma proposição tem-se: não (P e não P).
• Princípio do Terceiro excluído: “Toda proposição ou é verdadeira ou é falsa, não existindo um terceiro valor que ela possa assumir”. Sendo P uma proposição tem-se: P ou não P.

As proposições podem ser classificadas como simples ou compostas. A proposição será simples quando existir uma única afirmação na frase. Por outro lado, uma proposição é composta quando for constituída de, pelo menos, duas proposições simples “ligadas” por um conectivo lógico, também chamado de conector lógico, conectivo proposicional ou operação lógica.

Exemplificando

Observe as proposições A, B, C a seguir:

A: 11 é um número ímpar.

B: 11 é um número primo.

C: 11 é um número ímpar e primo.

As proposições A e B são compostas por uma única verdade.

A: verdadeira

B: verdadeira

Já a proposição C é composta por duas proposições simples (nesse caso, pelas proposições A e B) que são ligadas pela palavra “e”. A valoração da proposição C depende da valoração independente de A e de B, aplicada ao operador lógico que está unindo as duas proposições simples. Veremos em breve como fazer essa valoração.

Exemplos:

Exemplo a: Considere a frase: “Os suíços fabricam os melhores relógios e os franceses, o melhor vinho”. Se extrairmos as proposições simples das frases teremos:

P: Os suíços fabricam os melhores relógios.

S: Os franceses fabricam o melhor vinho.

Podemos reescrever a frase, utilizando uma notação simbólica, então o resultado será: P e S. Veja que temos a palavra “e” ligando as duas proposições simples.

Exemplo b: Considere a frase: “Se eu prestar atenção na aula, então tirarei boa nota na prova”. Novamente, se extrairmos as proposições simples das frases teremos:

A: Eu presto atenção na aula.

R: Eu tiro boa nota na prova.

Veja que ao extrair as proposições simples, podemos fazer adequações nos verbos, o mesmo acontece quando usamos proposições simples para fazer as compostas.

Exercício 1:

Considere as seguintes premissas:

1.    Todos os seres humanos são mortais.

2.    Sócrates é um ser humano.

Usando essas premissas, determine a conclusão lógica.

Solução:

Premissa 1: Todos os seres humanos são mortais.

Premissa 2: Sócrates é um ser humano.

A conclusão lógica que podemos tirar dessas premissas é:

Conclusão: Sócrates é mortal.

Isso segue a lógica do silogismo, que é uma forma comum de raciocínio lógico. O silogismo é uma forma de argumento em que se conclui uma proposição a partir de duas outras premissas que são relacionadas. Neste caso, a primeira premissa estabelece uma relação geral entre todos os seres humanos e sua mortalidade, e a segunda premissa identifica Sócrates como um ser humano específico. A conclusão lógica é que, se Sócrates é um ser humano, ele também é mortal, com base nas premissas dadas.

Exercício 2

Considere as seguintes premissas:

1.    Todos os mamíferos têm espinha dorsal.

2.    Todos os cães são mamíferos.

3.    Max é um cão.

Usando essas premissas, determine a conclusão lógica.

Solução:

Premissa 1: Todos os mamíferos têm espinha dorsal.

Premissa 2: Todos os cães são mamíferos.

Premissa 3: Max é um cão.

A conclusão lógica que podemos tirar dessas premissas é:

Conclusão: Max tem uma espinha dorsal.

A primeira premissa estabelece uma relação geral entre mamíferos e a presença de uma espinha dorsal. A segunda premissa afirma que todos os cães são mamíferos, e a terceira premissa identifica Max como um cão. Portanto, com base nas premissas, podemos concluir que Max, como um cão (que é um mamífero), também tem uma espinha dorsal.

Vamos Exercitar?

Chegou a hora de pensarmos como resolver seu desafio de lógica para a vaga de desenvolvedor trainee de uma grande empresa de tecnologia.

Imagine que você está concorrendo a uma vaga de desenvolvedor de software em uma empresa e precisa criar um programa que permita aos funcionários acessar áreas específicas com base em suas permissões. O sistema deve ser capaz de tomar decisões lógicas para permitir ou negar o acesso com base em premissas específicas.

Premissas:

• Existem três áreas de acesso na empresa: Sala A, Sala B e Sala C.
• Existem cinco funcionários: Alice, Bob, Carol, Dave e Eve.
• Cada funcionário tem um conjunto de permissões que define quais áreas ele pode acessar.
• Alice pode acessar a Sala A.
• Bob pode acessar a Sala A e a Sala B.
• Carol pode acessar a Sala B.
• Dave não tem permissão para acessar nenhuma sala.
• Eve pode acessar a Sala C.

Problema:

Como desenvolvedor da empresa, você foi encarregado de implementar um algoritmo que, com base nas premissas citadas anteriormente, determine se um funcionário específico tem permissão para acessar uma determinada área. O algoritmo deve receber o nome de um funcionário e o nome de uma área e retornar uma conclusão lógica sobre se o acesso deve ser permitido ou negado.

Conclusões:

Para resolver o problema, você pode usar a seguinte lógica:

1.  o funcionário tem permissão para acessar a área, a conclusão é “Acesso Permitido.”
2. Se o funcionário não tem permissão para acessar a área, a conclusão é “Acesso Negado.”

Aqui estão alguns exemplos de conclusões com base nas premissas:

• Se o funcionário for Alice e a área for Sala A, a conclusão é "Acesso Permitido."
• Se o funcionário for Bob e a área for Sala C, a conclusão é "Acesso Negado."
• Se o funcionário for Dave e a área for Sala B, a conclusão é “Acesso Negado.”

Você pode implementar esse algoritmo em uma linguagem de programação de sua preferência, e testá-lo com diferentes combinações de funcionários e áreas para verificar se ele está produzindo as conclusões corretas com base nas premissas fornecidas.

Este estudo de caso demonstra a aplicação de lógica e matemática computacional para resolver um problema prático de tomada de decisões com base em premissas definidas.

Saiba Mais

Os fundamentos da lógica são fundamentais para a compreensão da disciplina Lógica e Matemática Computacional. A seguir, algumas indicações para um estudo profundo sobre o tema.

• BISPO, C. A. F.; CASTANHEIRA, L. B.; FILHO, O. M. S. Introdução à lógica matemática. Cengage Learning Brasil, 2017. O capítulo 1 deste livro além de aborda de uma forma simples proposições em lógica e matemática computacional.
• ROSEN, K. H. Matemática discreta e suas aplicações. Grupo A, 2010. O capítulo 4 deste livro aborda de uma forma simples o tópico de proposições e sentenças.

Referências Bibliográficas

BISPO, F.; CASTANHEIRA, L. B. Introdução à lógica matemática. São Paulo: Cengage Learning, 2011.

GERSTING, J. L. Fundamentos matemáticos para a ciência da computação. Tradução de Valeria de Magalhaes Iorio. 7. ed. Rio de Janeiro: LTC, 2017.

MACHADO, N. J; CUNHA, M. O. da. Lógica e linguagem cotidiana: verdade, coerência, comunicação, argumentação. 2. ed. Belo Horizonte: Autêntica, 2008.

SANTOS, M. da S. dos et al. Lógica computacional. Porto Alegre: SAGAH, 2021.

Conectivos e classificação textual

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Olá, estudante! Iniciamos agora mais uma aulado nosso estudo de introdução à lógica proposicional. Nesta nova etapa, você aprenderá novos conectivos lógicos, o que lhe possibilitará valorar proposições compostas mais complexas, desenvolvendo suas habilidades de aplicar a lógica proposicional com suas regras e formas. Você já deve ter ouvido e falado muito frases do tipo “Se chover, eu não vou sair de casa”, ou então “Se eu ganhar na loteria, não vou mais trabalhar!”. Esse tipo de frase possui uma estrutura lógica embasada em uma condição: se algo acontecer, então outro evento também irá acontecer. Nesta seção, vamos entender esse tipo de estrutura lógica, bem como outros importantes conceitos.

Imagine que Carlos é um funcionário de uma empresa e está planejando suas férias de verão. Ele tem duas opções para suas férias: uma viagem à praia ou um passeio pelas montanhas.

Informações sobre Carlos:

1. Carlos gosta de ambas as opções, mas tem preferência por montanhas, pois gosta de esportes ao ar livre.

2. No entanto, Carlos também considera o fato de que alguns de seus amigos vão para a praia durante o mesmo período de férias.

Problema:

Carlos quer tomar uma decisão sobre onde passar suas férias de verão, considerando suas preferências pessoais e o desejo de passar um tempo com seus amigos.

Carlos está confrontando um dilema em relação à escolha de seu destino de férias de verão. Ele aprecia as duas opções disponíveis, mas deve decidir com base em suas preferências pessoais e outros fatores, como o desejo de passar um tempo com amigos que planejam uma viagem à praia durante o mesmo período de férias.

Por fim, ele precisa tomar uma decisão que leve em consideração suas preferências e a oportunidade de desfrutar da companhia de seus amigos na praia. A problematização se concentra na aplicação do conectivo lógico de disjunção (ou "ou") para resolver esse dilema.

Agora é com você! Para vencer esse desafio, nesta seção iremos aprender sobre os fundamentos da lógica, seus conectivos e por fim o conceito de fórmulas bem faturadas (fbf).

Vamos em frente para desvendar este mistério!

Vamos Começar!

Conectivo lógico de conjunção – e

Vamos começar estudando o conectivo lógico “e”, que também pode ser visto na literatura escrito em inglês AND ou ainda por meio do seu símbolo . Essa operação lógica é chamada conjunção e sua valoração será verdadeira somente quando ambas as proposições simples forem verdadeiras. Resumindo, se A e B forem proposições simples verdadeiras, a proposição composta A  B (lê-se “A e B”) será verdadeira. Para compreendermos melhor, considere as proposições a seguir:

A: Quatro é um número par.

B: Três é um número ímpar.

C: Cinco é maior que dez.

P: Quatro é um número par e três é um número ímpar

R: Quatro é um número par e cinco é maior que dez.

Vamos começar valorando as proposições simples (A, B, C): A: verdadeira. B: verdadeira. C: falsa.

Para facilitar nossa compreensão, vamos reescrever as proposições P, R utilizando notação simbólica, portanto temos:

P: A B 

R: A  C

Na proposição P temos que as proposições simples A, B são verdadeiras, portanto, P = V e V, o que resulta em verdadeiro, ou seja, a proposição P pode ser valorada como verdadeira. Já na proposição R, temos que A é verdadeiro, mas C é falso, portanto, R = V e F, o que resulta em falso, ou seja, a proposição R deve ser valorada como falsa, já que para essa operação lógica ambas as proposições precisam ser verdadeiras para o resultado também ser verdadeiro.

Conectivo lógico de disjunção – ou (inclusivo)

Outro conector muito utilizado tanto na Lógica Formal, quanto na computacional é “ou” que também pode ser visto na literatura escrito em inglês OR ou ainda por meio do seu símbolo  . Essa operação lógica é chamada de disjunção e seu operador lógico pode ser utilizado de duas formas distintas: inclusivo ou exclusivo. Veremos nesta seção a forma inclusiva do operador.

O operador lógico de disjunção usado na forma inclusiva terá sua valoração falsa somente quando ambas as proposições simples forem falsas. Resumindo, se A e B forem proposições simples falsas, a proposição composta A B (lê-se “A ou B”) será falsa, nos demais casos a valoração é verdadeira. Para compreendermos melhor, considere as proposições a seguir:

A: Quatro é um número par.

B: Três é um número ímpar.

C: Cinco é maior que dez.

D: Sete é um número par.

 P: Quatro é um número par ou três é um número ímpar.

R: Quatro é um número par ou cinco é maior que dez.

S: Cinco é maior que dez ou sete é um número par.

Vamos começar valorando as proposições simples (A, B, C, D):

A: verdadeira.

B: verdadeira.

C: falsa.

D: falsa

Para facilitar nossa compreensão, vamos reescrever as proposições P, R, S utilizando notação simbólica, portanto, temos:

P: A  B

R: A  C

S: C D

Na proposição P temos que as proposições simples A, B são verdadeiras, portanto, P = V ou V, o que resulta em verdadeiro, ou seja, a proposição P pode ser valorada como verdadeira. Na proposição R, temos que A é verdadeira, mas C é falsa, portanto, R = V ou F, como se trata da disjunção inclusiva, o resultado será verdadeiro, pois para ser falso ambas as proposições simples têm que ser falsas. Já na proposição S, temos que C, D são proposições simples falsas, portanto, S = F ou F, o que resultado em falso.

Siga em Frente...

Operador lógico de negação – não

Os operadores lógicos de conjunção e disjunção são binários, ou seja, juntam duas expressões para formar uma nova proposição. O operador lógico de negação é unário, ou seja, ele não junta duas proposições, ele age sobre uma única proposição (que pode ser resultado de uma operação binária). A palavra usada para fazer a negação é o não que também pode ser visto na literatura em inglês NOT, ou ainda de forma simbólica como ~, ¬, ‘. Os dois primeiros símbolos são usados antes da letra que representa a proposição, já o terceiro é usado depois da letra. Por exemplo, as expressões: ~ A, ¬B, C’ representam as negações das proposições A, B, C.

A operação lógica de negação troca o valor-verdade da proposição. Ou seja, se a proposição é verdadeira, quando acompanhada do operador de negação passará a ser falsa; por outro lado, se ela for falsa passará a ser verdadeira. Vejamos um exemplo, considere a proposição:

A: Luís gosta de viajar.

A negação de A (~ A ) pode ser lida como:

~ A: Luís não gosta de viajar.

Ou ainda como:

~ A: É falso que Luís gosta de viajar.

Ou ainda

~ A: Não é verdade que Luís gosta de viajar

Conectivo condicional (Implicação lógica) – se... então

Dadas as proposições simples A, B, elas formam uma condicional (ou implicação lógica) se for possível construir a estrutura: se A, então B. A primeira proposição é chamada antecedente, e a segunda consequente. A condicional significa que a verdade da primeira proposição implica a verdade da segunda proposição (Gersting, 2017). O símbolo usado para representar a implicação lógica é o →, logo a regra se A, então B, pode ser escrita como A → B.

Exemplificando

Considere as proposições a seguir: P: João estuda para a prova. R: João passa de ano. A proposição P → R (lê-se Se P, então R), deve ser traduzida como: Se João estudar para a prova, então passará de ano. Veja que para fazer sentido a composição da sentença condicionada, ajustamos os verbos estudar e passar. Mas o que realmente importa é entender a condição que foi criada. Veja que a proposição B está condicionada à proposição A, ou seja, B depende de A para acontecer.

Na valoração do condicional, se o antecedente e o consequente forem verdadeiros então o resultado será verdadeiro. Ou seja, V → V = V. Porém, se o antecedente for verdadeiro e o consequente for falso, o resultado será falso (V → F = F). Vejamos um exemplo:

A: O interruptor da sala foi desligado.

B: A luz da sala apagou.

C: A → B.

A proposição C deve ser traduzida como “Se o interruptor da sala for desligado, então a luz se apagará”. Se as duas proposições realmente acontecerem, então temos o caso V → V= V, ou seja, C é verdade. Porém, se o interruptor for desligado, mas por algum motivo a luz não se apagar, então temos o caso V → F = F, ou seja, C é falso.

Reflita Em um condicional existe o antecedente e o consequente, ou seja, uma proposição depende da outra. Se trocarmos a ordem do antecedente pelo consequente alteramos o resultado da condição? Quais implicações essa troca poderia trazer ao algoritmo?

Na construção de algoritmos, os condicionais são amplamente utilizados, veja o que nos diz um grande autor da área da computação: “Do ponto de vista computacional, uma condição é uma expressão booleana cujo resultado é um valor lógico falso ou verdadeiro. Assim, uma expressão booleana como condição é conseguida com uma relação lógica entre dois elementos e um operador relacional”. Veja que na computação usamos o mesmo recurso da Lógica Formal. A expressão booleana mencionada refere-se à álgebra Booleana que está embasada na Lógica Clássica. Uma expressão booleana é uma proposição que resultará em verdadeiro ou falso.

Na construção de algoritmos, o condicional aparece nas estruturas de decisão, também chamada Desvio Condicional. O nome “desvio” representa exatamente o que acontece em um algoritmo, quando aparece um condicional, pois dependendo do resultado (V ou F) o programa fará uma ação diferente. Por exemplo, imagine que estamos implementando um software para uma loja que oferece opções de pagamento à vista ou a prazo. Caso o comprador pague à vista ele terá um desconto de 10% na compra, que deve ser aplicado pelo próprio sistema. Pois bem, dadas as proposições:

A: Pagamento feito à vista.

B: Conceder desconto de 10%

No algoritmo deverá ser implementada a regra: A → B. “Se o pagamento for à vista, então será concedido um desconto de 10%”. A expressão “Se... então” é a mais comum de se utilizar para o condicional, até mesmo porque na construção de algoritmos usamos exatamente essas palavras. Mas a implicação lógica pode ser escrita de outras formas, conforme ilustra o Quadro 1, que nos apresenta oito formas diferentes de “traduzir” essa expressão lógica.

Expressão em português	Conectivo lógico	Expressão lógica
Se A, então B A condicional B A, logo B A só se B; A somente se B B segue de A A é uma condição suficiente para B Basta A para B B é uma condição necessária para A	Condicional	A → B

Quadro 1 | Expressões para condicional. Fonte: adaptado de Gersting (2017, p. 4).

Conectivo Bicondicional – se, e somente se

 Dadas as proposições simples A, B, elas formam uma bicondicional se for possível construir a estrutura: A se, e somente se, B. O símbolo usado para representar esse conectivo é o ↔, então a expressão A se, e somente se, B, pode ser expressa simbolicamente por A ↔ B. Vejamos um exemplo. Considere as proposições a seguir:

P: Lucas receberá o dinheiro.

Q: Lucas completará o trabalho. S: A ↔ B.

A proposição S, deve ser traduzida como “Lucas receberá o dinheiro se, e somente se, completar o trabalho”.

Segundo Gersting (2017), o bicondicional é um atalho para a expressão lógica: (A →B) ∧ (B → A). Nessa expressão temos a conjunção entre o resultado de duas condicionais que alteram seus antecedentes e consequentes. Para ficar mais claro, usando as proposições P, Q criadas anteriormente, dizer que “Lucas receberá o dinheiro se, e somente se, completar o trabalho” é o mesmo que dizer “Se Lucas receber o dinheiro então completará o trabalho e se Lucas completar o trabalho então receberá o dinheiro”. Como podemos observar, o bicondicional resume a sentença, facilitando até mesmo a compreensão. A valoração do conectivo bicondicional será verdadeira quando o valor- -lógico das duas proposições forem iguais, tanto para verdadeiro como para falso. Ou seja, V ↔ V =V e F ↔ F = V.

Fórmula bem-formulada ou fbf

Já sabemos que é possível criar proposições compostas, fazendo conexões entre proposições simples. Na verdade, podemos encadear preposições, conectivos e parênteses (ou colchetes) e formar novas expressões lógicas, as quais chamamos fórmula. Por exemplo, como a que vimos no conectivo bicondicional (A→ B) ∧ (B → A). Embora “Uma sequência qualquer de elementos do vocabulário do cálculo proposicional constitui uma fórmula”, nem toda fórmula é válida. Segundo Gersting (2017), certas regras de sintaxe precisam ser seguidas, assim como acontece em qualquer linguagem de programação. Podemos fazer uma analogia entre as fórmulas do cálculo proposicional com as fórmulas matemáticas. Os conectivos lógicos são como os operadores matemáticos (soma, subtração, etc.), portanto sempre teremos um conectivo entre duas proposições. O operador de negação é como o sinal negativo na matemática e, por isso, ele pode aparecer perto de outro conector. Uma fórmula que segue as regras de sintaxe é chamada de fórmula bem-formulada ou ainda, em inglês, well-formed fórmula – wff. Observe o Quadro 2. Nele temos três exemplos de fórmulas matemáticas, três de fórmulas válidas (fbf) e três de fórmulas inválidas.

Expressão matemática	fbf	Não fbf
(2+3)x5	(A → B)  C	AA  B
(3+4)x(2+3)	(A → B)  (B → A)	AB
2+3x-5	A → B C	B

Quadro 2 | Fórmulas matemáticas e proposicional

 

Vamos começar a analisar as fórmulas do Quadro 2 falando sobre os parênteses. Na fórmula matemática da linha 1, o resultado é 25, certo? E se não tivesse parênteses delimitando a adição, o resultado seria o mesmo? A resposta é não, o resultado seria 17, afinal a multiplicação tem precedência de resolução sobre a adição. Na fbf da linha 1 também temos parênteses e o motivo é o mesmo da expressão matemática: queremos que a condicional seja resolvida antes da disjunção. Portanto, os parênteses no cálculo proposicional também têm o papel de delimitar e indicar quais operações devem ser efetuadas primeiro. Assim como os operadores matemáticos, os conectivos lógicos também possuem ordem de precedência, sendo ela:

1. Para conectivos dentro de vários parênteses, efetuam-se primeiro as expressões dentro dos parênteses mais internos.

2. Negação (¬).

3. Conjunção e disjunção (˅˄).

4. Condicional (→).

5. Bicondicional (↔).

Quando dois operadores tiverem a mesma ordem de precedência, será valorado primeiro o que estiver mais à esquerda, da mesma forma que acontece em uma fórmula matemática.

Agora que sabemos a ordem de precedência dos conectivos lógicos, podemos interpretar a fbf da linha 2 no Quadro 2. Veja que primeiro será valorada a fórmula (A→ B), em seguida (B → A) e, por fim, a conjunção entre os dois resultados.

Já na fbf da linha 3, não temos parênteses, então devemos seguir a ordem de precedência e valorar da esquerda para direita. Então seria primeiro efetuada a negação ←C, em seguida seria calculado a conjunção de B com o resultado da negação: B ∧¬C e, por fim, seria feita a condicional entre A o resultado da conjunção.

Esse entendimento é muito importante, então vamos valorar a fbf da linha 3, dadas as seguintes entradas para as proposições A, B, C.

A é verdadeira.

B é falsa.

C é falsa.

Observe a Figura 1, ao submeter os valores-lógicos de entrada das proposições, seguindo a ordem de execução, tem-se a seguinte sequência:

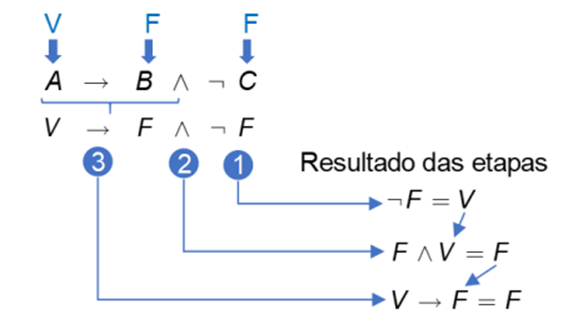
1. ¬F que resulta em V.

2. F ˄ V que resulta em F.

3. V→ F que resulta em F.

Portanto, o resultado da fbf A→ B ∧¬C é falso.

Ao observar o resultado das etapas na Figura 1, fica claro que o resultado de uma etapa é usado em outra etapa, pois a fórmula precisa ser resolvida em partes seguindo a ordem de precedência.

Por outro lado, a Figura 2 ilustra cada passo para a valoração da fórmula, para cada combinação possível de entrada. Como resultado lógico temos que para as entradas (1), (2) o resultado é F, já para a entrada (3) o resultado é V.

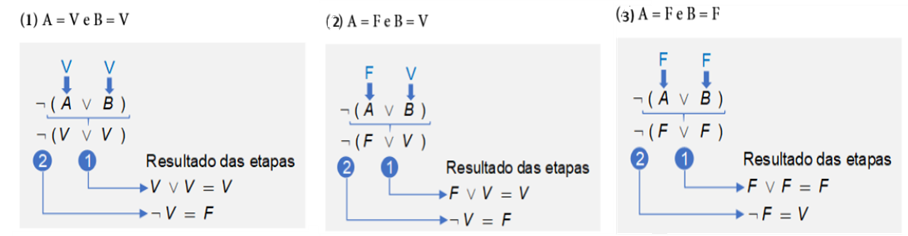
Agora vamos fazer a valoração da fórmula, do lado direito da equivalência, ou seja, ¬ A∧ ¬B, para cada uma das combinações possíveis de entrada. A Figura 3 ilustra cada passo para a valoração da fórmula. Como resultado lógico temos que para as entradas (1), (2), e (3) o resultado é F, já para a entrada (4) o resultado é V.

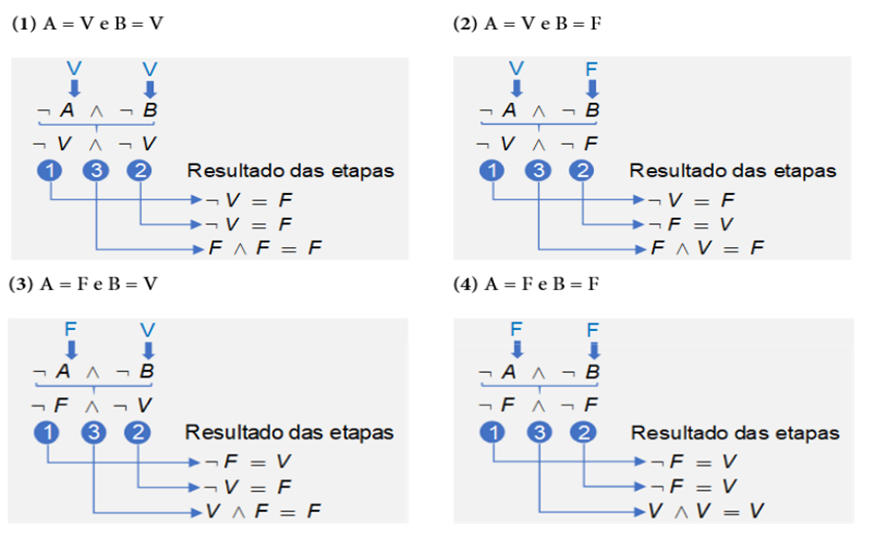
Como podemos ver, os resultados lógicos das fórmulas ¬(A ∨ B) e ¬ A∧¬B, para todas as combinações possíveis de entradas, são os mesmos, portanto demonstramos que essas fórmulas são equivalentes. Com essa demonstração, finalizamos nossa seção. Agora que já conhecemos todos os conectivos lógicos e como criar fórmulas válidas (fbf) para fazer a valoração de uma fbf, devemos seguir a ordem de precedência e ir resolvendo parte a parte da fórmula.

Até a próxima!

Vamos Exercitar?

Chegou a hora de pensarmos como resolver seu desafio de lógica para saber qual será o destino de Carlos em suas férias e qual decisão ele poderá tomar.

Carlos é um funcionário de uma empresa e está planejando suas férias de verão. Ele tem duas opções para suas férias: uma viagem à praia ou um passeio pelas montanhas.

Informações sobre Carlos:

1. Carlos gosta de ambas as opções, mas tem preferência por montanhas, pois gosta de esportes ao ar livre.

2. No entanto, Carlos também considera o fato de que alguns de seus amigos vão para a praia durante o mesmo período de férias.

Problema:

Carlos está confrontando um dilema em relação à escolha de seu destino de férias de verão. Ele aprecia as duas opções disponíveis, mas deve decidir com base em suas preferências pessoais e outros fatores, como o desejo de passar tempo com amigos que planejam uma viagem à praia durante o mesmo período de férias.

Carlos precisa tomar uma decisão que leve em consideração suas preferências e a oportunidade de desfrutar da companhia de seus amigos na praia. A problematização se concentra na aplicação do conectivo lógico de disjunção (ou "ou") para resolver esse dilema.

Solução:

Carlos pode usar o conectivo lógico de disjunção (ou "ou") para tomar sua decisão.

1.    A primeira opção é "Viagem à Praia." Vamos representar isso como "P" (praia).

2.    A segunda opção é "Passeio pelas Montanhas." Vamos representar isso como "M" (montanhas).

Agora, vamos aplicar o conectivo lógico "ou" para determinar a escolha de Carlos:

• Carlos prefere passeios pelas montanhas (M) OU
• Carlos quer passar tempo com seus amigos na praia (P)

As escolhas de Carlos podem ser representadas da seguinte forma:

(M) OR (P)

Usando a lógica de disjunção, Carlos pode escolher qualquer uma das opções. Se ele escolher "M," ele terá férias nas montanhas e desfrutará de esportes ao ar livre. Se ele escolher "P," ele terá férias na praia e passará tempo com seus amigos.

Portanto, usando a lógica de disjunção, Carlos pode tomar sua decisão com base em suas preferências pessoais ou seu desejo de passar tempo com seus amigos. Ele pode escolher uma das opções com base no que considera mais importante para suas férias de verão.

Saiba Mais

Os fundamentos da lógica são fundamentais para a compreensão da disciplina Lógica e Matemática Computacional. A seguir, algumas indicações para um estudo profundo sobre o tema.

1. BISPO, C. A. F.; CASTANHEIRA, L. B.; FILHO, O. M. S. Introdução à lógica matemática. Cengage Learning Brasil, 2017. O capítulo 1 deste livro aborda de uma forma simples proposições em lógica e matemática computacional, em especial, a classificação dos conectivos.
2. SILVA, F. S. C. da; FINGER, M.; MELO, A. C. V. de. Lógica para computação. 2. ed. Cengage Learning Brasil, 2018. O capítulo 1 aborda o tema de lógica proposicional e em específico os conectivos.

Referências Bibliográficas

BISPO, C. A. F.; CASTANHEIRA, L. B.; FILHO, O. M. S. Introdução à lógica matemática. Cengage Learning Brasil, 2017.

GERSTING, J. L. Fundamentos matemáticos para a ciência da computação: matemática discreta e suas aplicações. 7. ed. Rio de Janeiro: LTC, 2017.

ROSEN, K. H. Matemática discreta e suas aplicações. Grupo A, 2010.

SILVA, F. S. C. da; FINGER, M.; MELO, A. C. V. de. Lógica para computação. 2. ed. Cengage Learning Brasil, 2018.

Métodos dedutivos

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Olá, estudante! Dando continuidade ao nosso estudo de lógica computacional, chegou um momento muito importante no qual aprenderemos a fazer demonstrações lógicas. O raciocínio usado para fazer uma dedução lógica é similar ao usado para construir sequências lógicas em um algoritmo, pois, em ambos os casos, é necessário escrever uma sequência correta de passos, tanto em termos de sintaxe, quanto em relação ao raciocínio e às regras necessárias para alcançar o resultado desejado.

Você foi contratado para criar um sistema automatizado responsável por avaliar o desempenho dos estudantes em várias disciplinas e emitir relatórios de aprovação ou reprovação com base em critérios específicos. Este sistema deve ser capaz de processar resultados de provas em diferentes disciplinas e determinar se um aluno passou ou falhou de acordo com as regras da escola.

Problema a ser abordado:

O problema é desenvolver um sistema de avaliação de desempenho que possa avaliar automaticamente as notas dos alunos em várias disciplinas e determinar se eles passaram ou falharam de acordo com as regras da escola.

Para vencer esse desafio, você aprenderá nesta seção os conteúdos referentes aos métodos dedutíveis e à lógica proposicional que irão te auxiliar no desenvolvimento de estudo de caso e torná-lo um grande desenvolvedor.

Vamos em frente!

Vamos Começar!

Definição

Métodos dedutivos são uma abordagem lógica de raciocínio que envolve a aplicação de regras lógicas para chegar a conclusões a partir de premissas ou axiomas. Esses métodos desempenham um papel fundamental em várias disciplinas, incluindo lógica, matemática, filosofia e ciência da computação. Aqui estão algumas informações adicionais sobre métodos dedutivos:

• Premissas e conclusões: em um argumento dedutivo, você começa com premissas, que são afirmações iniciais consideradas verdadeiras, e aplica regras lógicas para derivar conclusões. A ideia é que, se as premissas são verdadeiras e as regras lógicas são válidas, então as conclusões também serão verdadeiras.
• Validade dedutiva: um argumento dedutivo é válido quando a estrutura lógica do argumento garante que, se todas as premissas são verdadeiras, a conclusão também será verdadeira. Se um argumento é válido e todas as premissas são verdadeiras, ele é considerado uma demonstração.
• Regras de inferência: as regras de inferência são diretrizes lógicas que governam como você pode passar de premissas para conclusões. Exemplos de regras de inferência incluem o modus ponens, modus tollens e silogismo hipotético na lógica proposicional.
• Lógica proposicional e de primeira ordem: na lógica proposicional, as afirmações são representadas por proposições, enquanto na lógica de primeira ordem, você lida com predicados e quantificadores. A lógica proposicional é usada quando se trabalha com afirmações simples, enquanto a lógica de primeira ordem é usada para expressar relações mais complexas e quantificação.
• Prova de teoremas: em matemática e lógica, a prova de teoremas é um exemplo clássico de aplicação de métodos dedutivos. Os matemáticos usam métodos dedutivos para provar teoremas, começando com axiomas e aplicando regras lógicas para chegar à conclusão.
• Sistemas formais: em muitos casos, os métodos dedutivos são aplicados em sistemas formais, em que a estrutura e as regras lógicas são rigorosamente definidas. Exemplos incluem sistemas axiomáticos como o sistema de Peano para a aritmética ou sistemas de prova assistida por computador, como o Coq.
• Aplicações na Ciência da Computação: na ciência da computação, a dedução lógica é usada em áreas como verificação formal de software, raciocínio baseado em conhecimento, resolução de problemas de IA e muitas outras aplicações.
• Limitações: embora os métodos dedutivos sejam poderosos para garantir a validade de argumentos, eles têm limitações. Eles dependem da qualidade das premissas e das regras lógicas usadas. Além disso, nem todos os problemas podem ser resolvidos de maneira dedutiva, levando ao uso de abordagens indutivas e abducentes em alguns casos.

Em resumo, os métodos dedutivos são uma ferramenta essencial para a análise lógica e a construção de argumentos válidos em diversas áreas do conhecimento, incluindo matemática, filosofia, ciência da computação e muito mais. Eles desempenham um papel crucial na garantia da validade de raciocínios e na resolução de problemas complexos.

Siga em Frente...

Lógica proposicional

A lógica proposicional é composta por proposições e conectivos lógicos que permitem criar uma série de fórmulas que quando escritas corretamente são chamadas fbfs (fórmula bem-formulada). Uma fbf é valorada em verdadeira (V) ou falsa (F), a partir da valoração das proposições com o conectivo lógico em questão, respeitando a ordem de precedência dos operadores lógicos. A valoração de uma fórmula também depende dos valores lógicos de entrada para cada uma das proposições. Por exemplo, dada a fórmula A ∧ B ∨ C ela será verdadeira ou falsa? A valoração depende dos valores lógicos de entrada para as proposições A, B, C. Observe a Figura 3.8a, na qual fazemos a valoração para as entradas A = V, B = V, C = F, veja que o resultado final é V. Considerando os valores lógicos: A = V, B = F, C = F, a mesma fórmula teve valoração final F (Figura 1). Portanto, a valoração de uma fbf depende das entradas lógicas e dos conectivos lógicos que são usados.

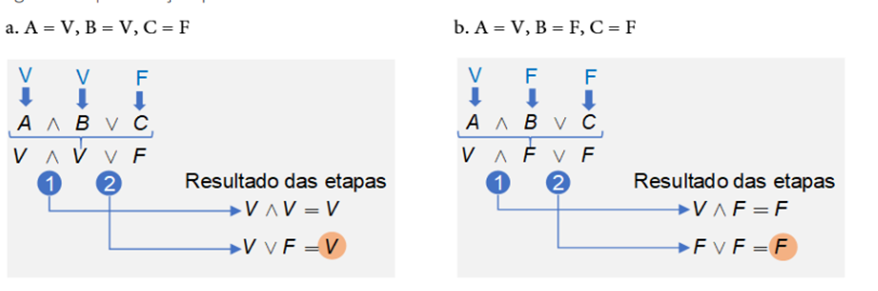
Quando uma fórmula apresenta um conjunto de proposições, das quais uma delas é uma conclusão, dizemos que tal fórmula é um argumento. “Um argumento é um conjunto de proposições, ou de fórmulas, nas quais uma delas (conclusão) deriva, ou é consequência, das outras (premissas)”. Um argumento pode ser representado de forma simbólica por:

$P_1\wedge P_2\wedge P_3\wedge \mathrm{...}{P}_n\to C$

Onde P₁, P₂, P₃, ..., P_n, são as hipóteses. Essas hipóteses podem ser tanto proposições simples, como uma fbf. A letra representa C a conclusão do argumento, a qual também pode ser tanto uma proposição simples como uma fbf.

ASSIMILE Um argumento é composto por hipóteses e conclusão, e ambas podem ser compostas por proposições simples ou fbf. No argumento, as proposições são ligadas logicamente pelo conectivo de conjunção (e), as quais implicam logicamente a conclusão. Por isso, a ligação entre as hipóteses e a conclusão é feita por meio do conectivo condicional.

Dado um argumento é importante validar se ele é válido ou inválido, o grande desafio é como fazer essa validação. A lógica possui mecanismos que permitem validá-lo, os quais são compostos pelas regras de equivalência e inferência lógica. Essas regras vão nos permitir avaliar a relação entre as hipóteses e a conclusão, que também pode ser chamada de consequência lógica, dedução lógica, conclusão lógica ou implicação lógica. “Uma proposição pode ser verdadeira ou falsa e não pode ser válida ou inválida; do mesmo modo, um argumento pode ser válido ou inválido e não pode ser verdadeiro ou falso”.

Exemplificando

Vamos analisar o seguinte argumento.

D. Pedro I proclamou a independência do Brasil e Thomas Jefferson escreveu a Declaração de Independência dos Estados Unidos. Portanto, todo dia tem 24 horas.

Vamos separar as proposições do argumento em hipóteses e conclusão.

A: D. Pedro I proclamou a independência do Brasil.

B: Thomas Jefferson escreveu a Declaração de Independência dos Estados Unidos.

 C: Todo dia tem 24 horas.

Nosso conhecimento nos permite valorar as três proposições, logo, A, B, C são todas verdadeiras. Embora, tanto as hipóteses, quanto a conclusão sejam proposições verdadeiras, o argumento é inválido, pois a conclusão nada tem a ver com as hipóteses.

Esse exemplo deixa claro que, basear-se apenas no conteúdo de um argumento não é suficiente para dizer se ele é válido ou não.

Segundo a Lógica Formal, devemos nos basear apenas nas regras para validar um argumento e não no conteúdo. O exemplo mencionado anteriormente deixa claro o motivo dessa restrição. Mas, afinal, quais são essas regras?

Para começarmos a entender as regras, vamos traduzir o argumento: D. Pedro I proclamou a independência do Brasil e Thomas Jefferson escreveu a Declaração de Independência dos Estados Unidos. Portanto, todo dia tem 24 horas, para notação simbólica, logo temos a seguinte fórmula: A ∧ B → C. Nessa fórmula quando o valor lógico de entrada da proposição A for verdadeiro e de B for falso, o resultado da implicação será falso, ou seja, existe pelo menos uma combinação de entradas, para a qual a fórmula resultará em falsa, logo essa fórmula não é uma tautologia e, consequentemente, não é um argumento válido. Tautologia é um resultado no qual todas as entradas possíveis de uma fórmula obtêm verdadeiro como resultado. Ainda, segundo a mesma autora, um argumento só é válido quando a fórmula é uma tautologia.

Reflita Um argumento composto por preposições verdadeiras não necessariamente é um argumento válido. Um argumento que contenha proposições falsas, pode ser um argumento válido?

Para saber se um argumento é válido ou não, precisamos saber se ele é uma tautologia. Para fazer essa checagem, poderíamos testar todas as combinações de entrada possíveis para o argumento. Porém, se tratando da Lógica Formal, podemos usar um sistema de regras de dedução e, seguindo uma sequência de demonstração provar se o argumento é válido ou não. “Uma sequência de demonstração é uma sequência de fbfs nas quais cada fbf é uma hipótese ou o resultado de se aplicar uma das regras de dedução do sistema formal a fbfs anteriores na sequência”. Para construir a sequência de demonstração, cada hipótese, que é uma proposição e que pode ser uma fbf, deve ser disposta conforme descrita na Tabela 1:

1- $P_1$	(hipótese)
2- $P_2$	(hipótese)
...	...
n) $P_n$	(hipótese)
n+1) $fb{f}_1$	(resultado da aplicação de uma regra de dedução à hipóteses anteriores)
n+2) $fb{f}_2$	(resultado da aplicação de uma regra de dedução à hipóteses anteriores)
...	...
n+n) C	(resultado da aplicação de uma regra de dedução à hipóteses anteriores)

Na sequência de demonstração, cada proposição deve ficar em uma linha, enumeramos para facilitar na hora de aplicar as regras de dedução. Na frente de cada linha devemos indicar o que ela representa, se é uma hipótese ou então a regra que foi aplicada. Após elencar todas as proposições é hora de começar a aplicar as regras e, consequentemente, obter novas fbfs. A quantidade varia de caso para caso, mas as regras de dedução devem ser aplicadas até que se consiga provar que o argumento é verdadeiro, ou então, que não existam mais regras a serem aplicadas, mostrando, assim, que o argumento é falso.

Exercício

Considere o argumento a seguir. Se George Washington foi o primeiro presidente dos Estados Unidos, então John Adams foi o primeiro vice-presidente. George Washington foi o primeiro presidente dos Estados Unidos. Portanto, John Adams foi o primeiro vice-presidente.

Este argumento tem duas hipóteses:

1.Se George Washington foi o primeiro presidente dos Estados Unidos, então John Adams foi o primeiro vice-presidente.

2.George Washington foi o primeiro presidente dos Estados Unidos.

Conclusão

John Adams foi o primeiro vice-presidente.

Uma representação simbólica desse argumento tem a forma (A → B) ∧ A → B

Uma tabela-verdade ou o algoritmo TestaTautologia mostra que esse argumento é uma tautologia. O argumento é válido; sua forma é tal que a conclusão segue, inevitavelmente, das hipóteses. De fato, essa forma de argumento, conhecida pelo nome em latim modus ponens (“método de afirmação”), é uma das regras de raciocínio que usaremos para construir a lógica proposicional.

Vamos Exercitar?

Chegou a hora de resolver o seu último desafio que é criar um sistema automatizado responsável por avaliar o desempenho dos estudantes em várias disciplinas e emitir relatórios de aprovação ou reprovação com base em critérios específicos. Este sistema deve ser capaz de processar resultados de provas em diferentes disciplinas e determinar se um aluno passou ou falhou de acordo com as regras da escola.

Problema a ser abordado:

O problema é desenvolver um sistema de avaliação de desempenho que possa avaliar automaticamente as notas dos alunos em várias disciplinas e determinar se eles passaram ou falharam de acordo com as regras da escola.

Solução:

A escola decide aplicar métodos dedutivos para criar um sistema de avaliação de desempenho baseado em valoração de fórmulas lógicas.

Etapas do estudo de caso:

• Definição de critérios de avaliação: a equipe de desenvolvimento começa definindo os critérios de avaliação para cada disciplina. Por exemplo, pode ser definido que um aluno precisa obter uma média de pelo menos 5,0 em Matemática para ser aprovado.
• Modelagem de fórmulas lógicas: para cada disciplina, são definidas fórmulas lógicas que especificam os critérios de aprovação. Por exemplo, "Média em Matemática >= 5,0" é uma fórmula que determina se um aluno passou em Matemática.
• Entrada de notas: os professores inserem as notas dos alunos em um sistema computacional que calcula automaticamente a média e aplica as fórmulas lógicas correspondentes.
• Valoração de fórmulas lógicas: o sistema avalia as fórmulas lógicas para cada disciplina com base nas notas do aluno. Se todas as fórmulas são verdadeiras, o aluno é aprovado na disciplina; caso contrário, é reprovado.
• Emissão de relatórios: o sistema gera automaticamente relatórios de aprovação ou reprovação para cada aluno, com base nas valorações das fórmulas lógicas. Os relatórios podem ser impressos e entregues aos alunos e seus responsáveis.
• Testes e verificação: a equipe realiza testes para garantir que o sistema avalie corretamente as notas e aplique as fórmulas lógicas de acordo com as regras da escola.

Resultado:

O estudo de caso mostra como a valoração de fórmulas lógicas pode ser aplicada na prática para avaliar o desempenho dos estudantes em diferentes disciplinas e determinar aprovações e reprovações automaticamente. Isso economiza tempo e recursos, garantindo que as regras da escola sejam rigorosamente seguidas.

Este estudo de caso ilustra uma aplicação prática de métodos dedutivos em matemática computacional, em que a valoração de fórmulas lógicas é usada para tomar decisões automáticas com base em critérios estabelecidos.

Saiba Mais

Métodos dedutíveis são fundamentais para a compreensão da disciplina Lógica e Matemática Computacional. A seguir, algumas indicações para um estudo profundo sobre o tema.

Fundamentos da lógica: Leitura do capítulo 1 do livro. GERSTING, J. L. Fundamentos matemáticos para a ciência da computação. Rio de Janeiro: Grupo GEN, 2016. O capítulo 1 deste livro aborda os tópicos referentes a: proposições, argumentos e exercícios referentes ao conteúdo ministrado.

Referências Bibliográficas

BISPO FILHO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à lógica matemática. São Paulo: Cengage Learning, 2017.

FAJARDO, R. Lógica matemática. 1. ed. São Paulo: Edusp, 2017.

MUNDIM, R. P. A Lógica Formal – princípios elementares. Revista Economia & Gestão, Belo Horizonte, v. 2, n. 3, jan./jun. 2002.

SANTOS, M. da S. dos et al. Lógica computacional. Grupo A, 2021.

Inferência lógica

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Olá, estudante! Dando continuidade ao nosso estudo de lógica computacional, chegou um momento muito importante no qual aprenderemos a fazer demonstrações lógicas. O raciocínio usado para fazer uma dedução lógica é similar ao usado para construir sequências lógicas em um algoritmo, pois, em ambos os casos, é necessário escrever uma sequência correta de passos, tanto em termos de sintaxe, quanto em relação ao raciocínio e às regras necessárias para alcançar o resultado desejado.

Dando continuidade ao processo seletivo para a vaga de trainee, nessa última fase do processo, os contratantes querem testar seu raciocínio lógico, bem como seu conhecimento sobre as regras de dedução da Lógica Formal. Você recebeu dois argumentos:

1. Se o papel de tornassol ficar vermelho, então a solução e ácida. O papel de tornassol ficou vermelho. Portanto, a solução é ácida.
2. Se treino, eu venço o campeonato de xadrez. Se não jogo vôlei, então eu treino xadrez. Não venci o campeonato de xadrez. Portanto, joguei vôlei.

Seu desafio é traduzir para forma simbólica os dois argumentos e provar a veracidade, usando as regras de dedução da Lógica Formal. Cada passo na sequência de demonstração deve ser comentado, para que os avaliadores tenham certeza de que você conhece o processo. Quantos passos serão necessários para demonstrar cada argumento? Será possível fazer uma demonstração usando somente regras de inferência? Sabendo que é mais importante conhecer o processo do que decorar regras, os avaliadores permitiram que você usasse a Internet para consultar as regras de equivalência e inferência lógica.

Seu desafio é traduzir para forma simbólica os dois argumentos e provar a veracidade, usando as regras de dedução da Lógica Formal. Cada passo na sequência de demonstração deve ser comentado, para que os avaliadores tenham certeza de que você conhece o processo. Quantos passos serão necessários para demonstrar cada argumento? Será possível fazer uma demonstração usando somente regras de inferência? Sabendo que é mais importante conhecer o processo do que decorar regras, os avaliadores permitiram que você usasse a Internet para consultar as regras de equivalência e inferência lógica.

Para vencer esse desafio, você verá nesta seção as regras para avaliar um argumento e verificar se ele é válido ou não. Também aprenderá como estruturar a sequência de demonstração, desenvolvendo, assim, o raciocínio e dando um passo a mais na direção de se tornar um grande desenvolvedor.

Vamos em frente!

Vamos Começar!

Regras de equivalência de dedução para a lógica proposicional

As regras de dedução são divididas em dois tipos: regras de equivalência e regras de inferência. Lembrando que duas fbfs (fórmula bem faturadas) são equivalentes, quando todas as combinações possíveis de entradas geram o mesmo resultado de saída para ambas as fbfs, as regras de equivalência serão usadas quando uma fbf (que pode ser uma hipótese ou resultado de uma regra) pode ser substituída por outra fbf, mantendo o resultado lógico. Por exemplo, se considerarmos a fbf que traduz uma das leis de De Morgan: ¬ (A ∨ B) ⇔ ¬A ∧¬B, em uma situação adequada podemos substituir a fbf ¬ (A ∨ B) por ¬ A ∧ ¬B, pois ambas são equivalentes. No Quadro 1 estão elencadas as regras de equivalência que iremos utilizar.

Expressão (fbf)	Equivalente (fbf)	Nome/abreviação
$\begin{array}{c}P\vee Q\\ P\wedge Q\end{array}$	$\begin{array}{c}Q\vee P\\ Q\wedge P\end{array}$	Comutatividade/com
$\begin{array}{c}(P\vee Q)\vee R\\ (P\wedge Q)\wedge R\end{array}$	$\begin{array}{c}P\vee (Q\vee R)\\ P\wedge (Q\wedge R)\end{array}$	Associatividade/ass
$\begin{array}{c}\neg (P\vee Q)\\ \neg (P\wedge Q)\end{array}$	$\begin{array}{c}\neg P\vee Q\\ \neg P\wedge Q\end{array}$	Leis de De Morgan/De Morgan
$P\to Q$	$\neg P\vee Q$	Condicional/cond
P	$\neg (\neg P)$	Dupla negação/dn
$P\leftrightarrow Q$	$(P\to Q)\wedge (Q\to P)$	Definição de equivalência/que

Quadro 1 | Conjuntos de regras de dedução

O Quadro 1 nos traz seis conjuntos de regras de dedução, sua utilização será da seguinte forma: Se tivermos uma expressão como da linha 1, Q ∨ P, quando necessário, podemos substitui-la por P ∨ Q, pois essas fbfs são equivalentes e trata-se da propriedade da comutatividade. O contrário também é válido, quando aparecer Q ∨ P, podemos substituir por P ∨ Q. Esse processo de substituir uma fbf por outra, é o mesmo para todas as demais regras apresentadas.

Siga em Frente...

Regras de inferência de dedução para a lógica proposional

Além das regras de equivalência, o processo de dedução lógica também possui as regras de inferência. Na inferência, dada uma determinada fbf, ela poderá ser substituída por outra que atenda à regra de inferência. Veja que aqui não é necessário ser uma tautologia (e realmente não será), mas é preciso seguir as regras da inferência.

A primeira regra de inferência que vamos estudar é chamada Modus Ponens (MP). Essa regra envolve uma implicação e uma conjunção e possui a seguinte estrutura: (P → Q) ∧ P → Q. Vejamos um exemplo para ficar mais clara a regra. Considerando o seguinte argumento: Se João receber seu salário, ele irá ao cinema, vamos separar as proposições P, Q, portanto:

P: João recebe o salário.

Q: João vai ao cinema.

Agora vamos representar cada parte da fórmula de Modus Ponens:

1. (P→ Q): Se João receber seu salário, ele irá ao cinema.
2. P: João recebe o salário.

Ao fazer a conjunção entre a primeira parte com a segunda, conseguimos inferir a conclusão, pois, se João receber seu salário, ele irá ao cinema E João recebeu o salário, logo podemos inferir (concluir) que João vai ao cinema.

A regra de Modus Ponens também pode ser representada pelo esquema:

$\begin{array}{c}P\to Q\\ \frac{P}{Q}\end{array}$

Aqui fica claro que quando se tem uma implicação e o antecedente é verdade, ento a conclusão é o consequente.

Outro importante regra de inferência é o Modus Tollens (MT). Essa regra, além de envolver uma implicação e uma conjunção, também envolve a negação de uma das proposições. Sua estrutura é dada pela fbf: (P →Q) ∧ ¬Q→ ¬P. Vejamos um exemplo. Considere o seguinte argumento:

Se João desligar o interruptor, então a lâmpada se apaga. Vamos separar as proposições P, Q, portanto:

P: João desliga o interruptor.

Q: A lâmpada apaga.

Agora vamos representar cada parte da fórmula de Modus Tollens:

1. (P → Q): Se João desligar o interruptor, então a lâmpada se apaga.
2.  ←Q: A lâmpada não apagou.

Ao fazer a conjunção entre a primeira parte com a segunda, conseguimos inferir a conclusão. Pois, se João desligar o interruptor, a lâmpada se apaga E a lâmpada não se apagou, logo podemos inferir (concluir) que João não desligou o interruptor.

Ao fazer a conjunção entre a primeira parte com a segunda, conseguimos inferir a conclusão. Pois, se João desligar o interruptor, a lâmpada se apaga E a lâmpada não se apagou, logo podemos inferir (concluir) que João não desligou o interruptor.

A regra de Modus Tollens também pode ser representada pelo esquema:

$\begin{array}{c}P\to Q\\ \frac{\neg Q}{\neg P}\end{array}$

Aqui fica claro que quando se tem uma implicação e o consequente não é verdade, então a conclusão é que o antecedente também não aconteceu.

Aqui fica claro que quando se tem uma implicação e o consequente não é verdade, então a conclusão é que o antecedente também não aconteceu.

Outra importante regra é o Silogismo Hipotético (SH). Nessa regra, além de existirem implicações e conjunções nas hipóteses, a conclusão também é uma implicação. Sua estrutura é dada pela fbf: (P → Q) ∧ (Q → R) → (P → R). Vejamos um exemplo. Considere o seguinte argumento: Se as árvores começam a florir, então começa a primavera. Se começa a primavera, então as árvores dão frutos. Vamos separar as proposições P, Q, R portanto:

P: As árvores começam a florir.

Q: A primavera começa.

R: As árvores dão frutos.

Agora vamos representar cada parte da fórmula de Silogismo Hipotético:

1.  (P →Q): Se as árvores começam a florir, então começa a primavera.
2. (Q → R): Se começa a primavera então as árvores dão frutos.

Ao fazer a conjunção entre a primeira parte com a segunda, conseguimos inferir a conclusão. Pois, se as árvores começam a florir, então começa a primavera E se começa a primavera então as árvores dão frutos, logo podemos inferir (concluir) que se as árvores começam a florir, então darão frutos.

A regra de Silogismo Hipotético também pode ser representada pelo esquema:

$\begin{array}{c}P\to Q\\ \frac{Q\to R}{P\to R}\end{array}$

Veja que a consequente de uma proposição é a antecedente na outra e, por isso, o resultado pode ser inferido do antecedente da primeira para a consequente da segunda proposição.

O Quadro 2 apresenta um resumo de algumas das principais regras de inferências. Além das regras já apresentadas, estão elencadas mais três regras à conjunção, na qual dadas duas proposições elas podem ser unidas por essa operação. A simplificação, que faz o contrário da conjunção, separa duas proposições. A adição, que adiciona uma nova proposição a uma já existente por meio de uma conjunção.

Expressão (fbf)	Equivalente (fbf)	Nome/abreviação
$\begin{array}{c}P\vee Q\\ P\wedge Q\end{array}$	Q	Modus Ponens/MP
$\begin{array}{c}(P\vee Q)\vee R\\ (P\wedge Q)\wedge R\end{array}$	$\neg P$	Modeus Tollens/MT
$\begin{array}{c}\neg (P\vee Q)\\ \neg (P\wedge Q)\end{array}$	$P\to R$	Silogismo Hipotético/SH
$P\to Q$	$P\vee Q$	Conjunção/conj
P	$P_{,}Q$	Simplificação/simp
$P\leftrightarrow Q$	$P\wedge Q$	Adição/ad

Quadro 2 | Regras de inferência:

Assimile Nas regras de equivalência, as colunas podem ser usadas nos dois sentidos. Já nas regras de inferência, só existe um sentido: a fbf da coluna “De” pode ser substituída pela coluna de “Podemos deduzir”, mas o contrário não é verdade. Em outras palavras, “Ao contrário das regras de equivalência, as regras de inferência não funcionam em ambas as direções”

Agora que já conhecemos as principais regras de dedução lógica, vamos utilizar esse método para mostrar que o argumento (¬A ∨ B) ∧ (B → C) → (A → C) é válido. O primeiro passo é identificar as hipóteses e a conclusão. A fórmula do argumento (P₁ ∧ P₂ ∧ P₃ ∧... P_n → C) nos diz que as hipóteses são ligadas pela conjunção e a conclusão é ligada pela última implicação lógica. Outro detalhe importante é que as hipóteses podem ser fbf e não somente proposições simples. Portanto, para nosso caso temos:

Hipótese 1: (¬A ∨ B)

Hipótese 2: (B → C)

Conclusão: (A → C)

Veja que na conclusão temos uma implicação, isso já nos dá indícios de que conseguiremos usar o silogismo hipotético. Vamos à sequência de demonstração.

1. ¬ A ∨ B (hip).

2. B → C (hip).

3. A → B (1, cond).

4. A → C (3, 4, SH)

Em quatro passos conseguimos demonstrar que o argumento é válido. Nos passos 1 e 2 elencamos as hipóteses. No passo 3, consultamos as regras de equivalência no Quadro 1, e usamos a regra de equivalência do condicional, ou seja, trocamos a hipótese ¬A ∨ B por A → B já que são equivalentes. Na linha 4, consultamos as regras de inferência no Quadro 3.6 e aplicamos o silogismo hipotético entre as linhas 3 e 2, ou seja, substituímos (A → B) ∧ (B → C) por A → C. Como chegamos exatamente a fbf da conclusão, provamos a validade do argumento. As regras de dedução lógica devem ser consultadas a todo momento no processo de demonstração. Não existe uma receita, somente a prática nos auxilia a desenvolvermos o raciocínio. Podemos fazer uma analogia do processo de demonstração com a atividade do programador. Na programação sequencial, temos uma entrada e uma saída desejável, portanto, implementamos uma sequência lógica de passos para chegar a esse resultado. É trabalho do desenvolvedor descobrir qual a sequência de proposições (comandos) que farão a transformação dos dados de entrada, para a saída. Cada linha do programa tem que seguir as regras de sintaxe da linguagem de programação, bem como a lógica necessária para alcançar o resultado. Portanto, praticar esse raciocínio de sequência lógica é um passo importante na formação do profissional de tecnologia.

Vamos Exercitar?

Chegou a hora de resolver seu último desafio do processo seletivo para a vaga de trainee em uma grande empresa de tecnologia. Você recebeu como desafio, avaliar dois argumentos, mostrando se eles são válidos ou não. Para isso, você deve usar as regras de dedução lógica. Relembrando os dois argumentos que lhe foram passados:

a. Se o papel de tornassol ficar vermelho, então a solução é ácida. O papel de tornassol ficou vermelho. Portanto, a solução é ácida.

b. Se treino, eu venço o campeonato de xadrez. Se não jogo vôlei, então eu treino xadrez. Não venci o campeonato de xadrez. Portanto, joguei vôlei.

Nessa etapa do desafio, você foi autorizado a usar a internet para consultar as regras de equivalência e inferência lógica.

Localizada uma fonte segura de informações, agora é preciso traduzir os argumentos para a forma simbólica e fazer a demonstração lógica. Vamos começar pelo argumento (a): 

a.    Se o papel de tornassol ficar vermelho, então a solução é ácida. O papel de tornassol ficou vermelho. Portanto, a solução é ácida.

Vamos traduzir o argumento para proposições:

P: O papel de tornassol fica vermelho.

Q: A solução é ácida.

Agora é possível traduzir o argumento para forma simbólica: (P → Q) ∧ P → Q. Agora podemos começar a sequência de demonstração, iniciando pela enumeração das hipóteses, seguida da aplicação de regras de dedução:

1.    P → Q (hip).

2.    P (hip).

3.    3. Q (1, 2 MP).

No item 1 tem-se a primeira hipótese P → Q. No segundo item, a segunda hipótese, lembrando que cada hipótese é conectada pela conjunção e, que cada uma delas pode ser fbf. Após elencar as hipóteses, consultamos o Quadro 1 e vimos que era possível aplicar a regra de Modus Ponens, ao aplicá-la na linha 3, chegamos exatamente na conclusão do argumento, logo esse argumento é válido

Agora vamos demonstrar o segundo argumento:

b.    Se treino, eu venço o campeonato de xadrez. Se não jogo vôlei, então eu treino xadrez. Não venci o campeonato de xadrez. Portanto, joguei vôlei.

Proposições:

P: Eu treino.

Q: Eu venci o campeonato de xadrez.

R: Eu jogo vôlei.

Forma simbólica do argumento: (P→Q) ∧ (¬R→P) ∧¬Q→R.

Sequência de demonstração:

1. P→ Q (hip).

2. ¬ R →P (hip).

3. ←Q (hip).

4. ←←P (1, 3, MT).

5. ←←R (2, 4, MT).

6. R (6, dn).

Para demonstrar esse argumento, foram necessários seis passos, sendo três deles as hipóteses. Após elencar as hipóteses, consultamos o Quadro 2 e vimos que era possível aplicar a regra de Modus Tollens entre os itens 1 e 3, com isso obtivemos o resultado ¬P no item 4. Também vimos que podíamos aplicar a mesma regra entre os itens 2 e 4, com isso obtivemos o resultado ¬¬R no item 5. Por fim, consultado o Quadro 1 vimos que podíamos aplicar a dupla negação no item 5 e obtivemos R no item 6. Como R é a conclusão, demonstramos que o argumento é válido.

Com essas demonstrações, finalizamos o desafio aplicando a lógica proposicional com suas formas e regras para resolver os mais diversos problemas.

Agora é só esperar o resultado positivo da empresa!

Saiba Mais

Inferência lógica são fundamentais para a compreensão da disciplina Lógica e Matemática Computacional. A seguir, algumas indicações para um estudo profundo sobre o tema.

1. Fundamentos da lógica: Leitura do capítulo 1 do livro. GERSTING, J. L. Fundamentos matemáticos para a ciência da computação. Rio de Janeiro: Grupo GEN, 2016. Nas páginas 26 e 27 você encontrará as Tabelas 1.11 e 1.12 contendo as regras de equivalência e inferência.
2. BISPO FILHO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à lógica matemática. São Paulo: Cengage Learning, 2017. O capítulo 5 deste livro aborda de uma forma muito clara as regras de inferência de dedução para a lógica proposicional.

Referências Bibliográficas

BISPO FILHO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à lógica matemática. São Paulo: Cengage Learning, 2017.

GERSTING, J. L. Fundamentos matemáticos para a ciência da computação: 7. ed. Rio de Janeiro: LTC, 2017.

ROSEN, K. H. Matemática discreta e suas aplicações. Grupo A, 2010.

SILVA, F. S. C. da; FINGER, M.; MELO, A. C. V. de. Lógica para computação. 2. ed. Cengage Learning Brasil, 2018. 

Videoaula de Encerramento

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

 

 

Ponto de Chegada

Olá, estudante! Para desenvolver a competência desta Unidade, que é conhecer os fundamentos da lógica matemática, você deverá primeiramente conhecer os conceitos fundamentais sobre: (a) premissas, conclusões e proposição, (b) operadores lógicos e fórmulas bem-faturadas (fbf), (c) métodos dedutíveis, (d) inferência lógica. Bom, então vamos lá.

Na primeira aula desta unidade foram abordados os tópicos referentes: premissas, conclusões e proposições. Esses elementos desempenham um papel central na construção de argumentos lógicos, inferências e cálculos computacionais. Vamos agora explorar mais a fundo essas definições:

• Premissas: são as afirmações iniciais ou condições fornecidas como base para um raciocínio lógico ou cálculo em lógica e matemática computacional.
• Conclusões: são as inferências ou os resultados obtidos a partir das premissas por meio de regras lógicas ou algoritmos em lógica e matemática computacional.
• Proposição: é uma declaração que pode ser verdadeira ou falsa e serve como uma unidade fundamental de informação em raciocínio lógico e cálculos computacionais em lógica e matemática computacional.

Na segunda aula, foram abordados os tópicos referentes aos conetivos lógicos, pois são peças-chave no universo da lógica e da matemática computacional. Em lógica e matemática computacional, os conectivos lógicos são operadores que permitem combinar, modificar ou avaliar a veracidade de proposições. Os conectivos mais comuns incluem "E" (conjunção), "OU" (disjunção), "NÃO" (negação), "SE... ENTÃO..." (implicação) e "SE E SOMENTE SE" (equivalência). Eles desempenham um papel fundamental na construção de expressões lógicas para representar raciocínios e cálculos, permitindo-nos realizar análises e tomar decisões lógicas de maneira precisa e estruturada.

Conetivos lógicos, pois são peças-chave no universo da lógica e da matemática computacional. Eles desempenham um papel essencial na construção de argumentos, na representação de relações entre proposições e na solução de problemas lógicos e computacionais. Estes operadores lógicos são ferramentas poderosas que permitem combinar e modificar proposições, tornando-os indispensáveis na programação, na tomada de decisões e em muitas outras aplicações. Vamos agora explorar o conceito fundamental dos conectivos lógicos.

Na terceira aula, foram abordados os tópicos referentes aos métodos dedutíveis, que são técnicas que partem de premissas ou princípios gerais e seguem regras lógicas para chegar a conclusões específicas. Esse processo de dedução é estruturado e garante a validade lógica das conclusões obtidas, desde que as premissas sejam verdadeiras e as regras lógicas sejam aplicadas corretamente. A dedução é fundamental na construção de argumentos sólidos, na solução de problemas lógicos e na formulação de provas matemáticas, entre outros contextos, em que a precisão e a coerência são essenciais.

Métodos dedutivos são um pilar central da lógica e do raciocínio, sendo amplamente empregados para estabelecer a validade de argumentos e inferências. Ao contrário dos métodos indutivos, que generalizam a partir de observações específicas, a dedução opera a partir de premissas gerais para obter conclusões específicas. Essa abordagem é essencial na matemática, filosofia e ciência da computação, garantindo a precisão e a validade dos resultados lógicos.

Por fim, na quarta aula foram abordados os tópicos referentes à inferência lógica. Em lógica e matemática computacional, inferência refere-se ao processo de deduzir conclusões lógicas com base em premissas, regras lógicas e princípios estabelecidos. Isso envolve a aplicação sistemática do raciocínio lógico para obter novas informações a partir das informações existentes. A inferência é usada em uma variedade de contextos, desde demonstrações matemáticas até sistemas de inteligência artificial, em que a capacidade de derivar conclusões válidas a partir de dados é fundamental. Ela desempenha um papel crítico na análise de informações, na resolução de problemas complexos e na tomada de decisões informadas em muitos domínios da ciência e da computação.

É Hora de Praticar!

Sistema de Aprovação de Empréstimos em um Banco

Definição:

O banco ABCXY está implementando um sistema automatizado de aprovação de empréstimos para seus clientes. Este sistema usará conectivos lógicos para determinar se um cliente é elegível para um empréstimo.

Problema:

O banco precisa estabelecer critérios de elegibilidade para empréstimos. Eles decidem usar três fatores para tomar essa decisão: histórico de crédito (C), renda mensal (R) e idade do cliente (A). Os critérios são definidos da seguinte forma:

O cliente deve ter um bom histórico de crédito (C) E uma renda mensal adequada (R) E ser maior de 18 anos (A >= 18) para ser elegível para um empréstimo.

Reflita

Como os conectivos lógicos podem ser aplicados para melhorar a eficiência e a precisão em áreas além da lógica matemática, como na tomada de decisões, na programação de computadores e na solução de problemas do mundo real?

Até que ponto os métodos dedutíveis podem ser usados para estabelecer a validade de argumentos complexos na vida cotidiana e em áreas como inteligência artificial e aprendizado de máquina, em que a lógica desempenha um papel fundamental?

Como a inferência lógica é fundamental para a capacidade de máquinas e sistemas de inteligência artificial tomarem decisões lógicas e responderem a situações complexas, e quais são os desafios associados à aplicação da inferência lógica em contextos do mundo real?

Resolução do estudo de caso

Solução:

O sistema de aprovação de empréstimos utiliza conectivos lógicos para combinar esses critérios da seguinte forma:

(C = Verdadeiro) **E** (R >= Valor Mínimo) **E** (A >= 18)

Onde "C = Verdadeiro" indica um bom histórico de crédito, "R >= Valor Mínimo" indica uma renda mensal adequada e "A >= 18" indica que o cliente tem mais de 18 anos.

Resultado:

O sistema de aprovação de empréstimos avalia automaticamente cada cliente com base nesses critérios e os conectivos lógicos. Se todos os critérios forem atendidos, o cliente é considerado elegível para o empréstimo. Caso contrário, a solicitação é rejeitada. Isso resulta em um processo eficiente e consistente de aprovação de empréstimos, reduzindo erros e garantindo que apenas os clientes elegíveis recebam empréstimos do banco ABCXY.

Dê o play!

Assimile

Referências

BISPO FILHO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à lógica matemática. São Paulo: Cengage Learning, 2017.

GERSTING, J. L. Fundamentos matemáticos para a ciência da computação: 7. ed. Rio de Janeiro: LTC, 2017.

ROSEN, K. H. Matemática discreta e suas aplicações. Grupo A, 2010.

SILVA, F. S. C. da; FINGER, M.; MELO, A. C. V. de. Lógica para computação. 2. ed. Cengage Learning Brasil, 2018.