Aplicações dos Conceitos Básicos

Capital de giro - desconto bancário

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você aprenderá algumas aplicações de conceitos básicos da Matemática Financeira como: capital de giro, desconto bancário e valor nominal, os quais podem ser encontrados em aplicações do nosso cotidiano, como: antecipar recebimentos de títulos para garantir capital de giro de uma empresa ou até mesmo antecipação de recebimento do 13º salário, entre outros. 
Para melhor compreender sobre o assunto, considere a situação do Lindolfo que trabalha numa empresa de telefonia; faltam três dias para ele receber o 13º salário e ele vai solicitar antecipação desse pagamento para quitar algumas dívidas. O salário de Lindolfo é R$ 1.800,00. Diante deste contexto, sabendo que uma instituição financeira lhe cobrará uma taxa nominal de 0,7% a.d., qual será o valor resgatado por Lindolfo?
Se você estivesse no lugar do Lindolfo, como faria para resolver essa situação? Para isso, vamos dar início ao nosso estudo!

Vamos Começar!

Capital de giro

No mercado de trabalho, muitas vezes, é o capital de giro que garante a saúde financeira das empresas. De acordo com Padoveze (2004), o termo “giro” vem da ideia de movimentação contínua dos principais elementos formadores das transações da empresa, em que ela basicamente forma seus lucros. 
Em outras palavras, ainda para Pandoveze (2004), da movimentação dos capitais aplicados no giro é que há a formação tradicional do lucro, ou seja, capital de giro é a terminologia utilizada para designar os valores investidos no ativo circulante, conjunto de bens e direitos que podem ser convertidos em dinheiro no considerado ano fiscal da empresa.
Segundo Gonçalves (2007), a expressão giro refere-se aos recursos em curto prazo da empresa, normalmente definidos como aqueles capazes de serem convertidos em dinheiro no prazo máximo de um ano (ciclo operacional) e que o capital de giro demonstra, em sentido amplo, o valor total dos recursos demandados pela empresa para financiar seu ciclo operacional, que reúne as necessidades circulantes identificadas desde a aquisição da matéria-prima até o recebimento das vendas.
Um exemplo de se obter o capital de giro e uma das formas de gerenciar esse capital é a partir do desconto bancário, o qual refere-se à obtenção de capital por meio antecipação de títulos, que podem ser boletos ou promissórias resultantes de vendas ou serviços prestados a clientes que pagarão numa relação futura.

Desconto bancário

O desconto bancário refere-se à antecipação no período em dias do recebimento de um título, seja por meio de promissória, boleto, entre outros, realizado por uma instituição financeira. Nos dias atuais, trata-se de uma operação comum entre pessoas jurídicas, que são empresas de grande, médio e pequeno porte, assim como também pessoas físicas. 
A pessoa jurídica, ou seja, instituição com responsabilidades jurídicas, empresas, associações, companhias, entre outras, pode realizar antecipações de diversos títulos, veja alguns exemplos:

• Promissórias;
• Duplicatas;
• Boletos;
• Cheques;
• Faturas de cartão de crédito.

A pessoa física, ou seja, todo indivíduo, homem ou mulher, identificado por um CPF (Cadastro de Pessoa Física), também pode fazer uso dessa operação financeira, observe alguns exemplos:

• 13º salário – 1ª e 2ª parcela. 
• Restituição de Imposto de Renda.

O recebimento antecipado de títulos não ocorre na sua totalidade, pois a instituição financeira cobra uma taxa administrativa pela realização dessa operação. O desconto bancário refere-se ao valor resultante da antecipação de um título, ou seja, é a quantia a ser abatida do valor nominal (valor do título).

Siga em Frente...

Valor nominal

O valor nominal (N) é denominado como valor do título que será antecipado, e as antecipações de títulos ocorrem geralmente a poucos dias do vencimento dos títulos, isso para que o valor resgatado (V_B ) seja o mais próximo do valor nominal (N), ou seja, do valor do título.
A taxa nominal é uma taxa de juros simples, então se necessitarmos convertê-la de mês para dia, ou de ano para dia, devemos usar o conceito de taxa equivalente em juros simples.
Para calcularmos o valor do desconto que será aplicado na antecipação de um título, ou seja, o desconto racional, é dado por:

$D=N·d·n$

Em que:

• N é o valor nominal.
• d corresponde a taxa de juros simples ao dia.
• n é o período de antecipação.

Agora, para o cálculo do valor resgatado (V_B), que é o valor nominal menos o desconto racional, fazemos uso da seguinte fórmula:

$V_B=N(1-dn)$

Para melhor compreender, observe um exemplo:
Ana, gerente de uma loja de roupas, necessita efetuar um pagamento e para isso antecipará o recebimento de uma duplicada no valor de R$ 1.100,00 vencendo em 7 dias. A instituição financeira que fará a antecipação da duplicata cobra uma taxa nominal administrativa de 17,1% a.m. Qual valor Ana resgatará pela duplicata?
Primeiramente, temos que uma taxa nominal (d) de 17,1% a.m., mas trabalhamos com taxa nominal ao dia. Logo, precisamos deixá-la equivalente, lembrando que a taxa nominal é taxa de juros simples:

$i_{eq}=\frac{\mathrm{0,171}}{30}=\mathrm{0,0057} a.d=\mathrm{0,57}\% a.d$

Assim, temos:

$d=\mathrm{0,57}\% a.d$

$N=R\$ \mathrm{1000,00}$

$n=7 dias$

Substituindo na fórmula do valor resgatado:

$V_B=N(1-dn)$

$V_B=1100(1-\mathrm{0,0057.7})$

$V_B=1100(1-\mathrm{0,0399})$

$V_B=1100\left(\mathrm{0,9601}\right)$

$V_B=1 \mathrm{056,11}$

Logo, o valor a ser resgatado por Ana é de R$ 1056,11.

Vamos Exercitar?

Para colocar em prática os conceitos vistos, considere a situação do Lindolfo que trabalha numa empresa de telefonia e faltam três dias para receber o 13º salário. O salário de Lindolfo é R$ 1.800,00 e ele vai antecipar o seu recebimento para pagar algumas dívidas. Diante deste contexto, sabendo que a instituição financeira lhe cobrará uma taxa nominal de 0,7% a.d., qual será o valor resgatado por Lindolfo? 
A segunda parcela do 13º salário, nesse caso, é título a ser antecipado, então:
N = R$ 1.800,00. 
A instituição cobra uma taxa nominal de 0,7% a.d. = d.
Lindolfo está a três dias de receber a segunda parcela do 13º salário e decide antecipar o seu recebimento, então n = 3. Substituindo na fórmula do valor resgatado:

$V_B=N(1-dn)$

$V_B=1800(1-\mathrm{0,007.3})$

$V_B=1800(1-\mathrm{0,021})$

$V_B=1800\left(\mathrm{0,979}\right)$

$V_B=\mathrm{1762,20}$

Portanto, pela antecipação do 13º salário em 3 dias, Lindolfo receberá R$ 1.762,20.

Saiba Mais

Para saber mais sobre capital de giro, leia o artigo Necessidade de capital de giro e sua aplicabilidade prática de José Bonifácio de Mateus Benatti. 

Referências Bibliográficas

ARAÚJO JÚNIOR, J. B. Uma breve introdução à matemática financeira: juros simples. Revista Processus Multidisciplinar, v. 1, n. 1, p. 29-38, 2020.
CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.
GONÇALVES, D. C. Capital de Giro. Disponível em: http://www.esacam.edu.br/jornal. Acesso em: 04 abr. 2024. 
PADOVEZE, C. L. Contabilidade gerencial: um enfoque em sistema de informação contábil. 4 ed. São Paulo: Atlas, 2004.

Desconto bancário com IOF

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você aprofundará ainda mais seus estudos sobre as aplicações de conceitos básicos da Matemática Financeira como: antecipações de títulos, Imposto sobre Operações Financeiras (IOF) e títulos de alto porte, os quais podem ser utilizados em antecipações de recebimentos de clientes. 
Para melhor compreender sobre o assunto, considere a situação do gerente Paulo, que precisa trocar os equipamentos do setor da linha de produção de uma metalúrgica e para isso fará a antecipação de um título de valore nominal:

• Título: R$ 23.650,00

O título vencerá em 17 dias em uma instituição financeira que cobra pela transação uma taxa nominal de 0,12% a.d. e IOF de 0,017% a.d. Qual será o valor resgatado por Paulo?
Se você estivesse no lugar do Paulo, como faria para resolver essa situação? Para isso, vamos dar início ao nosso estudo!

Vamos Começar!

Antecipação de títulos

Nos dias atuais, a antecipação de títulos pode ser uma ferramenta útil para os gestores de empresas dos mais diversos setores, uma vez que os desafios na gestão de uma empresa são inúmeros, sejam eles, fatores internos ou externos, de modo que o planejamento financeiro não ocorre da forma esperada.

A antecipação de títulos consiste em receber de forma antecipada valores de títulos de crédito como duplicatas, notas promissórias, cheques, entre outros, com vencimentos futuros, para que a empresa possa ter esse dinheiro em caixa para movimentações financeiras. 
Em outras palavras, a antecipação de títulos permite que um valor a ser creditado no futuro seja realocado para o presente. No caso de um negócio que realiza vendas a prazo, a antecipação de títulos possibilita acesso aos recursos de maneira imediata, sem ser necessário esperar o vencimento desses títulos.
Uma observação importante é que as antecipações de títulos ocorrem geralmente a poucos dias do pagamento dos clientes, isso para que o valor resgatado seja o mais próximo do valor nominal, ou seja, do valor do título.
Veja um exemplo: João vai receber a primeira parcela do seu 13º salário no dia 30 de novembro, mas irá antecipar esse recebimento para o dia 10 de novembro, logo ele terá um desconto do valor nominal devido aos 20 dias de antecipação.

IOF

O Imposto sobre Operações Financeiras (IOF) foi criado pela Lei nº 5.143, de 1966, com intuito de substituir o imposto sobre transferência para o exterior. O IOF envolve operações de câmbio, crédito, seguro ou relativas a títulos ou valores imobiliários. Quando estamos trabalhando com desconto bancário, antecipação de títulos, promissórias e duplicatas, o IOF se apresenta conforme a fórmula a seguir:

$V_B=N[1-(d+IOF\left)n\right]$

Em que:

• VB: valor descontado, valor resgatado, valor resultante da antecipação.
• N: valor nominal, valor do título antecipado.
• d: taxa nominal, taxa de juros simples, ao dia.
• n: período de antecipação do título, geralmente em dias.
• IOF: Imposto sobre Operações Financeiras, taxa de juros simples, ao dia.

Importante ressaltar que a taxa nominal e o IOF são taxas de juros simples, então se necessitarmos convertê-las de mês para dia, ou de ano para dia, usaremos o conceito de Taxa Equivalente em Juros Simples.
Um exemplo de antecipação de títulos com incidência do IOF são títulos de alto porte, que veremos a seguir.

Siga em Frente...

Títulos de alto porte

Os títulos que têm incidência do IOF são denominados como alto porte, identicamente à taxa de desconto, este percentual é calculado sobre o valor nominal do título juntamente com uma taxa nominal cobrada no ato da liberação dos recursos, de forma antecipada (SANTOS, 2016).
De acordo com Santos (2016), as operações de desconto praticadas pelas instituições financeiras costumam apresentar encargos financeiros, os quais são geralmente cobrados sobre o valor nominal do título (valor de resgate) e pagos à vista (descontados no momento da liberação dos recursos).
Vejamos um exemplo de como podemos aplicar o conceito de antecipação em títulos de alto porte. 
Marina pretende antecipar um título de alto porte no valor de R$ 17.500,00 em 15 dias e consultou que o valor do resgate seria de R$ 12.000,00. Sabendo que o IOF cobrado foi de 0,05% a.d., qual a taxa nominal cobrada nessa antecipação?
Primeiramente, vamos utilizar a fórmula da antecipação de títulos com IOF.

$V_B=N[1-(d+IOF\left)n\right]$

Na sequência, vamos extrair as informações do problema:

$V_b=12000$

$N=17500$

$d=?$

$n=15 dias$

$IOF=0,05\%=0,0005 a.d.$

Depois, vamos substituir os seguintes valores:

$V_B=N[1-(d+IOF\left)n\right]$

$12.000=17.500[1-(d+0,0005\left)15\right]$

$\frac{12.000}{17.500}=[1-(d+0,0005\left)15\right]$

$0,7=[1-(d+0,0005\left)15\right]$

$0,7=[1-(15d+0,0075\left)\right]$

$0,7=[1-15d-0,0075]$

$0,7=0,9925-15d$

$15d=0,9925-0,7$

$15d=0,2925$

$15d=0,2925$

$d=\frac{0,2925}{15}$

$d=0,0195 a.d$

$d=1,95\% a.d$

Portanto, a taxa nominal cobrada nessa antecipação foi de 1,95% a.d.

Vamos Exercitar?

Para colocar em prática os conceitos vistos, considere a situação do gerente Paulo, que precisa trocar os equipamentos do setor da linha de produção de uma metalúrgica e para isso fará a antecipação de um título de valor nominal R$ 23.650,00.
O título vencerá em 17 dias em uma instituição financeira que cobra pela transação uma taxa nominal de 0,12% a.d. e IOF de 0,017% a.d. Qual será o valor resgatado por Paulo?
Primeiramente, vamos extrair as informações do problema:

$V_b=?$

$N=23650$

$d=0,12\% a.d=0,0012 a.d$

$n=17 dias$

$IOF=0,017\%=0,00017 a.d.$

Substituindo os valores na fórmula:

$V_B=N[1-(d+IOF\left)n\right]$

$V_B=23.650[1-(0,0012+0,00017\left)17\right]$

$V_B=23.650[1-(0,00137\left)17\right]$

$V_B=23.650[1-0,02329]$

$V_B=23.650.0,9767$

$V_B=23099,19$

Logo, o valor resgatado será de R$ 23.099,19. 

Saiba Mais

Para saber mais sobre IOF, leia o artigo Imposto sobre operações financeiras, câmbio e a novíssima Lei Nº 14.286 de 2021  de Luiz Henrique Nicolau. 

Referências Bibliográficas

ARAÚJO JÚNIOR, J. B. Uma breve introdução à matemática financeira: juros simples. Revista Processus Multidisciplinar, v. 1, n. 1, p. 29-38, 2020.

CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.

GONÇALVES, D. C. Capital de Giro. Disponível em: http://www.esacam.edu.br/jornal. Acesso em: 04 abr. 2024.

PADOVEZE, C. L. Contabilidade gerencial: um enfoque em sistema de informação contábil. 4. ed. São Paulo: Atlas, 2004.

SANTOS, J. C. Matemática financeira. Londrina: Editora e Distribuidora Educacional S/A, 2016, 216 p. 

Taxa efetiva e taxa nominal

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você compreenderá sobre a importância da utilização de forma adequada das taxas equivalentes nos regimes de capitalização de juros simples e juros compostos, ou seja, a taxa efetiva e taxa nominal. 
Com intuito de aprofundar e aplicar os conceitos vistos, considere a situação de Lilian, que precisa financiar a compra de um equipamento da linha de produção de uma empresa e terá a seguinte condição de pagamento:

• Pagar uma entrada e financiar o restante em parcelas mensais e iguais, sob a taxa nominal de 13,2% a.a. em regime de juros compostos.

Considerando tal situação, agora, você deve apresentar de forma adequada a taxa de juros da proposta de pagamento da Lilian. Para isso, vamos dar início ao nosso estudo!

Vamos Começar!

Taxa equivalente

A taxa equivalente, seja no regime de capitalização de juros simples ou compostos, tem como função adequar a taxa à relação temporal de trabalho. Para uma melhor compreensão, observe um exemplo:
Se temos uma situação em que as parcelas são mensais, a taxa de juros também precisa estar ao mês (a.m.). O mesmo ocorre se as parcelas estiverem ao ano (a.a.), logo, é necessário converter a taxa de juros também ao ano, utilizando os conceitos de taxas equivalentes para cada regime de capitalização.
Importante relembrar que no período comercial, temos o seguinte:

• 1 mês = 30 dias
• 1 ano = 12 meses 
• 1 ano = 360 dias
• 1 bimestre = 2 meses
• 1 trimestre = 3 meses
• semestre = 6 meses

Sendo assim, a taxa equivalente só altera a relação temporal, pois quando temos alteração de regime de capitalização de juros simples para compostos, ou vice-versa, trabalhamos com taxa efetiva ou nominal.

Siga em Frente...

Taxa efetiva

A taxa efetiva refere-se a uma taxa em que a unidade de tempo é igual à unidade de tempo do período de capitalização específico para o regime de juros compostos. Para converter uma taxa nominal em efetiva usa-se a seguinte fórmula:

$i_{ef}={\left(\frac{d}{n}+1\right)}^f-1$

Em que:

• n: período da taxa nominal, em dias.
• f: período da taxa efetiva, em dias.
• d: taxa nominal.

Observe um exemplo:
José vai realizar um financiamento em regime de juros compostos, o qual apresentou taxa nominal de 32% a.a. Qual é a taxa de trabalho desse financiamento ao ano?
Como se trata de um financiamento em juros compostos, a taxa de trabalho não pode ser a taxa nominal, pois ela é taxa de juros simples; então deveremos trabalhar com taxa efetiva. Extraindo informações da situação, temos:
n = 360 dias.

f = 360 dias.

d = 32% = 0,32

Substituindo na fórmula:

$i_{ef}={\left(\frac{d}{n}+1\right)}^f-1$

$i_{ef}={\left(\frac{\mathrm{0,32}}{360}+1\right)}^{360}-1$

$i_{ef}={\left(\mathrm{0,0009}+1\right)}^{360}-1$

$i_{ef}=\mathrm{1,3824}-1$

$i_{ef}=\mathrm{0,3824} a.a=\mathrm{38,24}\% a.a$

Logo, a taxa efetiva para o financiamento é 38,24% a.a.

Taxa nominal

A taxa nominal refere-se a uma taxa em que a unidade de tempo é igual à unidade de tempo do período de capitalização dos juros simples. Para converter uma taxa efetiva em nominal usa-se a seguinte fórmula:

$d={\left[\right(i_{ef}+1)}^{\frac{1}{f}}-1]n$

Em que:

• n: período da taxa nominal, em dias.
• f: período da taxa efetiva, em dias.
• d: taxa nominal.
• $i_{ef}$: taxa efetiva.

Para melhor compreender, observe um exemplo: 
Alana vai realizar um financiamento em regime de juros simples, mas como o parcelamento é a curto prazo, apresentou taxa efetiva de 27% a.a. Qual é a taxa de trabalho desse financiamento ao ano?
Como se trata de um financiamento em juros simples, a taxa de trabalho não pode ser a taxa efetiva, pois ela é taxa de juros compostos; então deveremos trabalhar com taxa nominal.

• n =  360 dias
• f = 360 dias
• ${ i}_{ef}=27\%=\mathrm{0,27}$

Substituindo na fórmula, temos:

$d={\left[\right(i_{ef}+1)}^{\frac{1}{f}}-1]n$

$d={\left[\right(\mathrm{0,27}+1)}^{\frac{1}{360}}-1]360$

$d={\left[\right(\mathrm{1,27})}^{\mathrm{0,0028}}-1]360$

$d=[\mathrm{1,0007}-1]360$

$d=[\mathrm{1,0007}-1]360$

$d=\mathrm{0,0007.360}$

$d=\mathrm{0,252} a.a$

$d=\mathrm{25,2}\% a.a$

 

Portanto, a taxa de trabalho, que é a taxa nominal é de 25,2% a.a.

Vamos Exercitar?

Para colocar em prática os conceitos vistos, considere a situação de Lilian, que precisa financiar a compra de um equipamento da linha de produção de uma empresa e terá a seguinte condição de pagamento:

• Pagar uma entrada e financiar o restante em parcelas mensais e iguais, sob a taxa nominal de 13,2% a.a. em regime de juros compostos.

Considerando tal situação, agora, você deve apresentar de forma adequada a taxa de juros da proposta de pagamento da Lilian.
Como a proposta trata de um financiamento em parcelas mensais e iguais em regime de juros compostos, não calcularemos as parcelas com a taxa nominal, pois ela é uma taxa de juros simples, por isso vamos converter a taxa dada em taxa efetiva ao mês.

• n = 360 dias
• f = 30 dias
• d = 13,2% = 0,132

Substituindo na fórmula, temos: 

$i_{ef}={\left(\frac{d}{n}+1\right)}^f-1$

$i_{ef}={\left(\frac{\mathrm{0,132}}{360}+1\right)}^{30}-1$

$i_{ef}={\left(\frac{\mathrm{0,132}}{360}+1\right)}^{30}-1$

$i_{ef}={\left(\mathrm{0,0004}+1\right)}^{30}-1$

$i_{ef}=\mathrm{1,0121}-1$

$i_{ef}=\mathrm{0,0121} a.m=\mathrm{1,21}\% a.m$

Portanto, a taxa de que iremos usar para calcular as parcelas mensais e iguais da proposta, que é a taxa efetiva, será de 1,21% a.m.

Saiba Mais

Para saber mais sobre taxas, acesse o livro Matemática financeira de Ernesto Coutinho Puccini.

Referências Bibliográficas

ARAÚJO JÚNIOR, J. B. Uma breve introdução à matemática financeira: juros simples. Revista Processus Multidisciplinar, v. 1, n. 1, p. 29-38, 2020.
CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.
PADOVEZE, C. L. Contabilidade gerencial: um enfoque em sistema de informação contábil. 4 ed. São Paulo: Atlas, 2004.
PUCCINI, A. L. Matemática financeira. Projeto universidade aberta, 2007.

Negociação de juros simples e compostos

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você aprenderá sobre negociação em regime de juros simples e compostos, bem como analisar propostas e contrapropostas, aplicando conceitos de séries de ambos os regimes de capitalização. 
Para melhor compreender sobre o assunto, considere a situação de Kátia, que pretende comprar um carro e ofereceu a seguinte proposta de pagamento: uma entrada de R$ 25.670,40 a uma taxa de juros efetiva de 1,21% a.m., mais três parcelas mensais e iguais. A loja fez uma contraproposta de três parcelas iguais a R$ 22.000,00 com vencimento a cada 10 dias, sob a taxa de juros simples de 4% a.d. Considerando isso, qual é o valor de cada parcela da proposta de Kátia?
Para isso, vamos dar início ao nosso estudo!

Vamos Começar!

Negociação em juros simples

O ato de negociar faz parte de nossas vidas, pois a partir disso é que adquirimos bens de consumo dentro de nossas reais possibilidades, sem depreciar o valor real do bem. A negociação tem como princípio um fundamento básico: o capital numa situação A deve ser o mesmo numa situação B, ou seja, o capital do anúncio tem que ser o mesmo do proposto, independentemente da forma de pagamento e regime de juros.

• $C_A=C_B$
• $C_A$ = capital numa situação “A”
• $C_B$ = capital numa situação “B”

Podemos ter situações que envolvem o pagamento de entrada, daí temos a seguinte situação:

${\mathrm{AV}}_A={\mathrm{AV}}_B$

$A{V}_A$ = valor à vista na situação “A”

$A{V}_B$ = valor à vista na situação “B”

Observe um exemplo: uma loja de departamento masculina está anunciando um terno por duas parcelas iguais de R$ 300,00 a cada sete dias, sob regime e taxa de juros simples de 0,035% a.d. Ricardo tem muito interesse pelo terno e apresentou uma proposta de pagar em três parcelas iguais, vencendo a cada dez dias, sob a mesma taxa e o mesmo regime imposto pela loja. Qual é o valor das parcelas propostas pelo Ricardo?
Vamos substituir na fórmula a condição anunciada e a condição proposta: 

${AV}_{Anunciado}={AV}_{Proposto}$

${\sum }_{j=1}^j\frac{M_{jAnunciada}}{1+i_{Anunciada}{n}_{jAnunciado}}={\sum }_{j=1}^j\frac{M_{jProposta}}{1+i_{Proposta}{n}_{jProposta}}$

$\frac{300}{(1+\mathrm{0,00035.7})}+\frac{300}{(1+\mathrm{0,00035.14})}=\frac{M}{(1+\mathrm{0,00035.10})}+\frac{M}{(1+\mathrm{0,00035.20})}+\frac{M}{(1+\mathrm{0,00035.30})}$

$\mathrm{597,81}=\mathrm{2,9791}M$

$\frac{\mathrm{597,81}}{\mathrm{2,9791}}=M$

$M=\mathrm{200,67}$

Logo, o valor de cada parcela proposta por Carlos é R$ 200,67.

Siga em Frente...

Negociação em juros compostos

Assim como vimos na negociação de juros simples, podemos utilizar os mesmos conceitos para os juros compostos, com a diferença da utilização da série de juros compostos. 
Exemplo: um aparelho celular está sendo anunciado por duas parcelas mensais e iguais a R$ 600,00, sob o regime de juros compostos de 1,8% a.m. Carlos pretende comprar o aparelho celular, mas ofereceu a seguinte condição: 3 parcelas iguais vencendo em 2, 3 e 5 meses, sob taxa e regime de juros compostos de 2,0% a.m. Qual é o valor das parcelas propostas por Carlos?
Vamos substituir na fórmula a condição anunciada e a condição proposta. 

${AV}_{Anunciado}={AV}_{Proposto}$

${\sum }_{j=1}^j\frac{M_{jProposta}}{{\left(1+i_{Proposta}\right)}^{n_{jProposta}}}={\sum }_{j=1}^j\frac{M_{jProposta}}{{\left(1+i_{Proposta}\right)}^{n_{jProposta}}}$

$\frac{600}{{\left(1+\mathrm{0,018}\right)}^1}+\frac{600}{{\left(1+\mathrm{0,018}\right)}^2}=\frac{M}{{\left(1+\mathrm{0,02}\right)}^2}+\frac{M}{{\left(1+\mathrm{0,02}\right)}^3}+\frac{M}{{\left(1+\mathrm{0,02}\right)}^5}$

$\frac{600}{\mathrm{1,018}}+\frac{600}{\mathrm{1,0363}}=\frac{M}{\mathrm{1,0404}}+\frac{M}{\mathrm{1,0612}}+\frac{M}{\mathrm{1,1041}}$

$\mathrm{589,39}+\mathrm{578,98}=\left(\frac{1}{\mathrm{1,0404}}+\frac{1}{\mathrm{1,0612}}+\frac{1}{\mathrm{1,1041}}\right)M$
$\mathrm{1168,37}=\left(\mathrm{0,9612}+\mathrm{0,9423}+\mathrm{0,9057}\right)M$

$\mathrm{1168,37}=\mathrm{2,8092}M$

$\frac{\mathrm{1168,37}}{\mathrm{2,8092}}=M$

$M=\mathrm{415,91}$

Logo, o valor de cada parcela proposta por Carlos é R$ 415,91.

 

Negociação em juros simples e compostos

Podemos ter também numa mesma negociação ambos os regimes de capitalização, juros simples e juros compostos. Veja o exemplo:
Renata está vendendo um aparelho eletrônico por duas parcelas de R$ 150,00 a cada 12 dias, sob regime e taxa de juros simples de 0,043% a.d. Joana quer pagar em duas parcelas mensais e iguais sob regime e taxa de juros compostos de 1,32% a.m. Qual é o valor das parcelas que Joana está disposta a pagar?

${AV}_{Anunciado}={AV}_{Proposto}$

${\sum }_{j=1}^j\frac{M_{jAnunciada}}{1+i_{Anunciada}{n}_{jAnunciado}}={\sum }_{j=1}^j\frac{M_{jProposta}}{{\left(1+i_{Proposta}\right)}^{n_{jProposta}}}$

$\frac{150}{1+\mathrm{0,00043}·12}+\frac{150}{1+\mathrm{0,00043}·24}=\frac{M}{{\left(1+\mathrm{0,0132}\right)}^1}+\frac{M}{{\left(1+\mathrm{0,0132}\right)}^2}$

$\mathrm{297,70}=\mathrm{1,9611}M$

$M=\frac{\mathrm{297,70}}{\mathrm{1,9611}}$

$M=R\$\mathrm{151,80}$

Portanto, o valor das parcelas propostas por Joana é de R$ 151,80. 

Vamos Exercitar?

Para colocar em prática os conceitos vistos, considere a situação de Kátia, que pretende comprar um carro e ofereceu a seguinte proposta de pagamento: uma entrada de R$ 25.670,40 a uma taxa de juros efetiva de 1,21% a.m., mais três parcelas mensais e iguais. Mas a loja fez uma contraproposta de três parcelas iguais a R$ 22.000,00 com vencimento a cada 10 dias, sob a taxa de juros simples de 0,4% a.d. Considerando isso, qual valor de cada parcela da proposta de Kátia?
Primeiramente, temos o valor anunciado e valor proposto:

${AV}_{Anunciado}={AV}_{Proposto}$

${\sum }_{j=1}^j\frac{M_{jAnunciada}}{1+i_{Anunciada}{n}_{jAnunciado}}=E_{Proposta}+{\sum }_{j=1}^j\frac{M_{jProposta}}{{\left(1+i_{Proposta}\right)}^{n_{jProposta}}}$

$\frac{22.000}{1+\mathrm{0,0004}·10}+\frac{22.000}{1+\mathrm{0,0004}·20}+\frac{22.000}{1+\mathrm{0,0004}·30}=$

$=\mathrm{25.670,40}+\frac{M}{{\left(1+\mathrm{0,0121}\right)}^1}+\frac{M}{{\left(1+\mathrm{0,0121}\right)}^2}+\frac{M}{{\left(1+\mathrm{0,0121}\right)}^3}$

$\mathrm{65.476,88}=\mathrm{25.670,40}+M\left(\frac{1}{\mathrm{1,0121}}+\frac{1}{\mathrm{1,0243}}+\frac{1}{\mathrm{1,0367}}\right)$

$\mathrm{65.476,88}-\mathrm{25.670,40}=M(\mathrm{0,9880}+\mathrm{0,9763}+\mathrm{0,9646})$

$\mathrm{39.806,48}=\mathrm{2,9289}M$

$M=\frac{\mathrm{39.806,48}}{\mathrm{2,9289}}$

$M=R\$\mathrm{13.590,93}$

Portanto, o valor das parcelas propostas é de R$ 13.590,93. 

Saiba Mais

Para saber mais sobre negociação, leia o livro Matemática financeira de Fernando Guerra e Inder Jeet Taneja.

Referências Bibliográficas

ARAÚJO JÚNIOR, J. B. Uma breve introdução à matemática financeira: juros simples. Revista Processus Multidisciplinar, v. 1, n. 1, p. 29-38, 2020.

CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.

GUERRA, F.; TANEJA, I. J. Matemática Financeira. Curso de graduação em Administração a Distância, v. 1, 2014.

PADOVEZE, C. L. Contabilidade gerencial: um enfoque em sistema de informação contábil. 4 ed. São Paulo: Atlas, 2004.

Videoaula de Encerramento

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Chegada

Para desenvolver a competência desta unidade, que é compreender os conceitos relacionados a descontos e à taxa efetiva e nominal a fim de utilizá-los na resolução de problemas que envolvam negociações financeiras, é necessário elencar os conhecimentos a seguir.
Quando trabalhamos com desconto bancário, nos referimos à antecipação do recebimento de títulos no período em dias, seja por meio de promissória, boleto, entre outros, realizado por uma instituição financeira.
Para calcularmos o valor do desconto que será aplicado na antecipação de um título, ou seja, o desconto racional, utilizamos a seguinte fórmula:

$D=N·d·n$

Em que:

• N: valor nominal.
• d: corresponde a taxa de juros simples ao dia.
• n: período de antecipação.

Agora, para o cálculo do valor resgatado ($V_B$), utilizamos a seguinte fórmula:

$V_B=N(1-dn)$

Também podemos trabalhar com desconto bancário de títulos de alto porte, ou seja, com IOF, a partir da seguinte fórmula:

$V_B=N[1-\left(d+IOF\right)n]$

Em que:

• $V_B$: valor descontado, valor resgatado, valor resultante da antecipação.
• N: valor nominal, valor do título antecipado.
• d: taxa nominal, taxa de juros simples, ao dia.
• n: período de antecipação do título, geralmente em dias.
• IOF: Imposto sobre Operações Financeiras, taxa de juros simples, ao dia.

Outro tema importante para área refere-se às conversões das taxas equivalentes, em que a taxa de juros e o período precisam estar na mesma unidade tempo. Para o regime de juros compostos utilizamos a taxa efetiva e para sua conversão usa-se a seguinte fórmula:

$i_{ef}={\left(\frac{d}{n}+1\right)}^f-1$

Em que:

• n: período da taxa nominal, em dias.
• f: período da taxa efetiva, em dias
• d: taxa nominal

A taxa nominal refere-se a uma taxa no regime de capitalização dos juros simples. Para converter uma taxa efetiva em nominal usa-se a seguinte fórmula:

$d={\left[\right(i_{ef}+1)}^{\frac{1}{f}}-1]n$

Em que:

• n: período da taxa nominal, em dias.
• f: período da taxa efetiva, em dias
• d: taxa nominal 
• $i_{e}f$: taxa efetiva

Por fim, temos que a negociação tem como princípio um fundamento básico: o capital numa situação A deve ser o mesmo numa situação B, ou seja, o capital do anúncio tem que ser o mesmo do proposto, independentemente da forma de pagamento e regime de juros.

${AV}_{Anunciado}={AV}_{Proposto}$

Para negociação com anúncio e proposta em juros simples usa-se a fórmula:

${\sum }_{j=1}^j\frac{M_{jAnunciada}}{1+i_{Anunciada}{n}_{jAnunciado}}={\sum }_{j=1}^j\frac{M_{jProposta}}{1+i_{Proposta}{n}_{jProposta}}$

Para negociação com anúncio e proposta em juros compostos usa-se a fórmula:

${\sum }_{j=1}^j\frac{M_{jProposta}}{{\left(1+i_{Proposta}\right)}^{n_{jProposta}}}={\sum }_{j=1}^j\frac{M_{jProposta}}{{\left(1+i_{Proposta}\right)}^{n_{jProposta}}}$

Para negociação com anúncio em juros simples e proposta em juros compostos usa-se a fórmula:

${\sum }_{j=1}^j\frac{M_{jAnunciada}}{1+i_{Anunciada}{n}_{jAnunciado}}={\sum }_{j=1}^j\frac{M_{jProposta}}{{\left(1+i_{Proposta}\right)}^{n_{jProposta}}}$

Importante ressaltar que podemos ter anúncio em juros compostos e proposta em juros simples também. Tais conceitos vistos nesta unidade além de contribuir para o avanço dos conteúdos da disciplina também visam contribuir para resolução de problemas do nosso dia a dia.

É Hora de Praticar!

Agora, você colocará em prática os conceitos vistos nesta unidade. Vamos lá!
Dona Maria alugou um forno para sua padaria e vai pagar duas parcelas mensais e iguais a R$ 650,00 sob regime de juros compostos e taxa efetiva de 4% a.m. Senhor José, dono da padaria ao lado, também tem interesse em alugar a mesma máquina, mas tem condição para pagar em três vezes mensais e iguais sob regime de juros compostos e taxa efetiva de 4% a.m. 
Sendo assim, qual o valor de cada parcela Seu José vai pagar?

Reflita

Após o estudo, reflita sobre as seguintes perguntas:

• Você consegue identificar qual fórmula utilizar em cada situação-problema?
• Você extrai as informações de forma correta dos problemas?
• Você consegue identificar situações do seu dia a dia em nossa disciplina e como ela pode te ajudar?

 

Dê o Play!

Clique aqui para acessar os slides do Dê o play!

Resolução do estudo de caso

Primeiramente temos que: 

• Situação A (Anúncio): duas parcelas mensais e iguais a R$ 650,00 sob regime de juros compostos e taxa efetiva de 4% a.m.
• Situação B (Proposta): três vezes mensais e iguais sob regime de juros compostos e taxa efetiva de 4% a.m. 

Observe que não será necessário converter as taxas, pois temos taxa efetiva no regime de juros compostos. Neste caso, temos tanto o anúncio quanto a proposta em regime de juros compostos, então vamos utilizar a seguinte fórmula:

$\sum _{j=1}^j\frac{M_{j_A}}{{\left(1+i_A\right)}^{n_{jA}}}=\sum _{j=1}^j\frac{M_{j_B}}{{\left(1+i_B\right)}^{n_{jB}}}$

Substituindo os valores, temos:

$\frac{650}{{\left(1+\mathrm{0,04}\right)}^1}+\frac{650}{{\left(1+\mathrm{0,04}\right)}^2}=\frac{M}{{\left(1+\mathrm{0,04}\right)}^1}+\frac{M}{{\left(1+\mathrm{0,04}\right)}^2}+\frac{M}{{\left(1+\mathrm{0,04}\right)}^3}$

$\frac{650}{\mathrm{1,04}}+\frac{650}{\mathrm{1,0816}}=\frac{M}{\mathrm{1,04}}+\frac{M}{\mathrm{1,0816}}+\frac{M}{\mathrm{1,1249}}$

$625+\mathrm{600,96}=M\left(\frac{1}{\mathrm{1,04}}+\frac{1}{\mathrm{1,0816}}+\frac{1}{\mathrm{1,1249}}\right)$

$\mathrm{1.225,96}=M\left(\mathrm{0,9615}+\mathrm{0,9246}+\mathrm{0,8890}\right)$

$\mathrm{1.225,96}=\mathrm{2,7751}M$

$M=\frac{\mathrm{1.225,96}}{\mathrm{2,7751}}$

$M=\mathrm{441,77}$

Logo, o valor de cada parcela da proposta do sr. José é R$ 441,77.

Dê o play!

Assimile

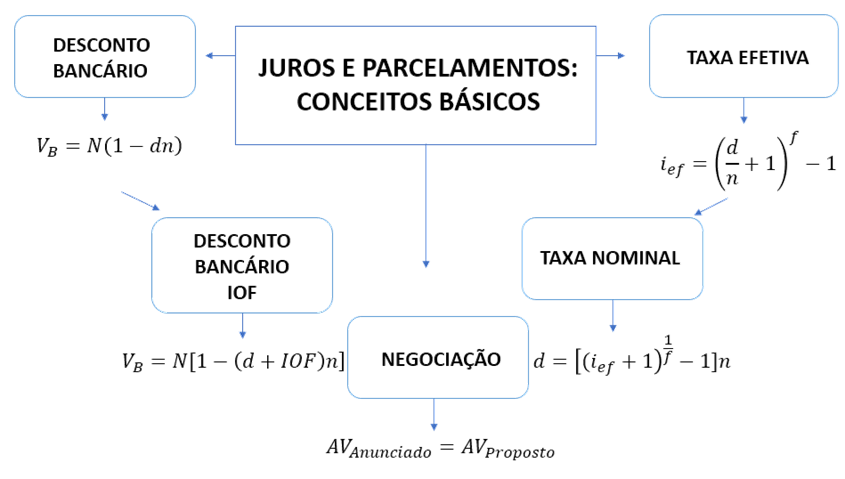
Referências

CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.

MOREIRA, F. R. et al. Juros: conceitos e aplicações. Enciclopédia Biosfera, v. 6, n. 9, 2010.

OLIVEIRA, W. Sistema de juros compostos. Revista Processus Multidisciplinar, v. 1, n. 1, p. 11-22, 2020.