Estatística Inferencial

Estimativas de confiança

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Nossas decisões são fundamentadas em conhecimentos anteriores e experiências similares, visando otimizar benefícios e reduzir possíveis impactos adversos. No entanto, devemos reconhecer que a margem de erro está sempre presente. Nesse contexto, a estatística inferencial, como um campo da estatística, procura quantificar as probabilidades de ocorrência de erros e acertos nas escolhas que fazemos.

A estatística inferencial é uma área da estatística que desempenha um papel importante na avaliação e na mensuração desses erros e acertos na tomada de decisões. Ela utiliza métodos estatísticos para fazer inferências pautadas em amostras de dados e estender essas conclusões para populações maiores. A estatística inferencial permite quantificar a incerteza associada a uma decisão ou conclusão com base em dados limitados, o que ajuda a avaliar as chances de erros e acertos.

Nesta aula, iniciaremos nossos estudos sobre a estatística inferencial, discutindo o teorema do limite central e os intervalos de confiança. Para entender como podemos aplicar esse conceito, considere que um fabricante pretende investigar a longevidade das baterias utilizadas em relógios de pulso. Uma amostra de diversos lotes produzidos pela mesma empresa foi sujeita a testes de aceleração, e os resultados para a durabilidade em anos foram os seguintes: 1,2 – 1,4 – 1,7 – 1,3 – 1,2 – 2,3 – 2,0 – 1,5 – 1,8 – 1,4 – 1,6 – 1,5 – 1,7 – 1,5 – 1,3. Assumindo que a durabilidade das baterias segue uma distribuição normal e que tenha desvio-padrão 1, qual é o intervalo de confiança para a média do tempo de duração dessas baterias, com 90% de confiança?

Para confirmar isso, precisamos aprender como realizar o cálculo de um intervalo de confiança.

Bons estudos!

Vamos Começar!

A estatística inferencial, às vezes denominada estatística indutiva, abrange um conjunto de métodos que possibilitam a obtenção de conclusões sobre uma população (estimando valores desconhecidos da população) com base na análise de dados amostrados. Ao examinarmos uma amostra de indivíduos com pressão arterial elevada por meio de testes inferenciais, podemos inferir que um indivíduo típico dessa população tem, por exemplo, uma probabilidade de 60% de sofrer um ataque cardíaco. É importante notar que essa análise é realizada em uma amostra, já que seria impraticável examinar toda a população de pessoas com pressão arterial elevada. No entanto, com base nos resultados obtidos dessa amostra, fazemos inferências que se aplicam à totalidade da população em questão.

Um resultado importante utilizado na estatística inferencial é o Teorema do Limite Central (TLC), que estabelece a conexão entre a distribuição amostral da média e a população da qual as amostras são extraídas. Essa teoria é uma ferramenta essencial, pois fornece as informações necessárias quando são realizadas inferências estatísticas sobre a média de determinada população (Larson; Farber, 2015). De acordo com o Teorema do Limite Central:

Quando amostras aleatórias de tamanho $n$, onde $n\ge 30$, , são retiradas de uma população com uma média $\mu$ e um desvio-padrão $\sigma$, a distribuição amostral da média se aproxima de uma distribuição normal. Essa aproximação se torna mais precisa à medida que o tamanho da amostra aumenta, conforme ilustra a Figura 1.

Se as amostras aleatórias de tamanho $n$ são retiradas de uma população que segue uma distribuição normal, então a distribuição amostral das médias amostrais também é normal para qualquer tamanho de amostra $n$ (Larson; Farber, 2015).

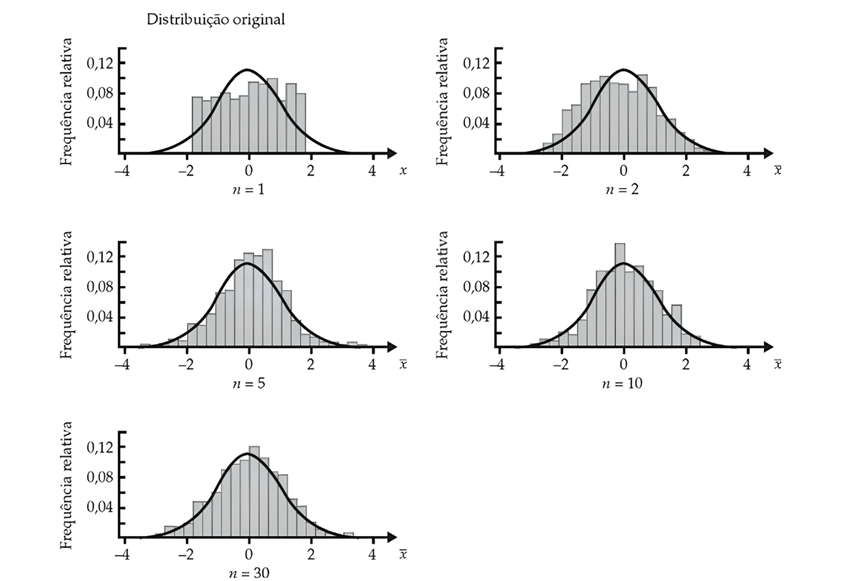
Em ambos os cenários citados, a média da distribuição amostral da média é equivalente à média da população. Além disso, a variância da distribuição amostral da média é igual a $\frac{{\sigma }^2}{n}$, onde ${\sigma }^2$ é a variância da população, e o desvio-padrão da distribuição amostral da média é $\frac{\sigma }{\surd n}$, sendo $n$ o tamanho da amostra.

Um resultado importante relacionado ao TLC refere-se à probabilidade de uma média amostral: “A distribuição da média amostral $\overline{)x}$ de uma amostra aleatória $n$ extraída de uma população não normal, com média $\mu$ e desvio-padrão $\sigma$, é aproximadamente normal, com média $\mu$ e desvio-padrão $\frac{\sigma }{\surd n}$" (Werkema, 2014, p. 22). Isso quer dizer que:

 

$z=\frac{\overline{)x}-\mu }{\sigma ⁄\surd n}$

É aproximadamente normal com média 0 e variância 1, isto é $N(0,1)$.

Siga em Frente...

Com base nos conceitos que discutimos até agora, vamos abordar dois exemplos.

 

Exemplo 1

Suponha que você esteja realizando um estudo sobre a média de tempo que motoristas dirigem por dia. Para isso, você selecionou uma amostra de 50 motoristas que, em média, dirigem 25 minutos por dia. Considerando que o desvio-padrão é $\sigma =1,5$ minuto, qual é a probabilidade de que a média de tempo que esses motoristas passam dirigindo todos os dias seja entre 24,6 e 25,7 minutos?

Dado que o tamanho da amostra excede 30, podemos empregar o teorema do limite central para inferir que a distribuição das médias amostrais é aproximadamente normal com média $\mu =25$ e desvio-padrão $\frac{1,5}{\surd 50}$. Vamos determinar os z-escores:

$z_1=\frac{24,6-25}{\frac{1,5}{\surd 50}}\approx -1,88$

$z_2=\frac{25,7-25}{\frac{1,5}{\surd 50}}\approx 3,30$

Assim, queremos $P(24,6\le x \le 25,7)$= $P(-1,88\le Z\le 3,30)$, conforme ilustra a Figura 2.

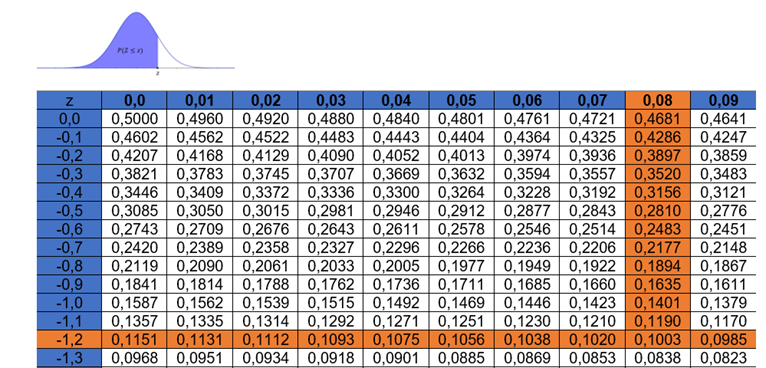
Com o auxílio de uma tabela da distribuição normal padrão (Tabela 1), devemos encontrar a área correspondente a cada z-escore e, depois, realizar uma subtração entre a área maior e a área menor. Para determinar a área relacionada ao z-escore negativo, lembre-se de que a curva normal é simétrica, então $P(Z\le z)=P(Z\ge z)$.

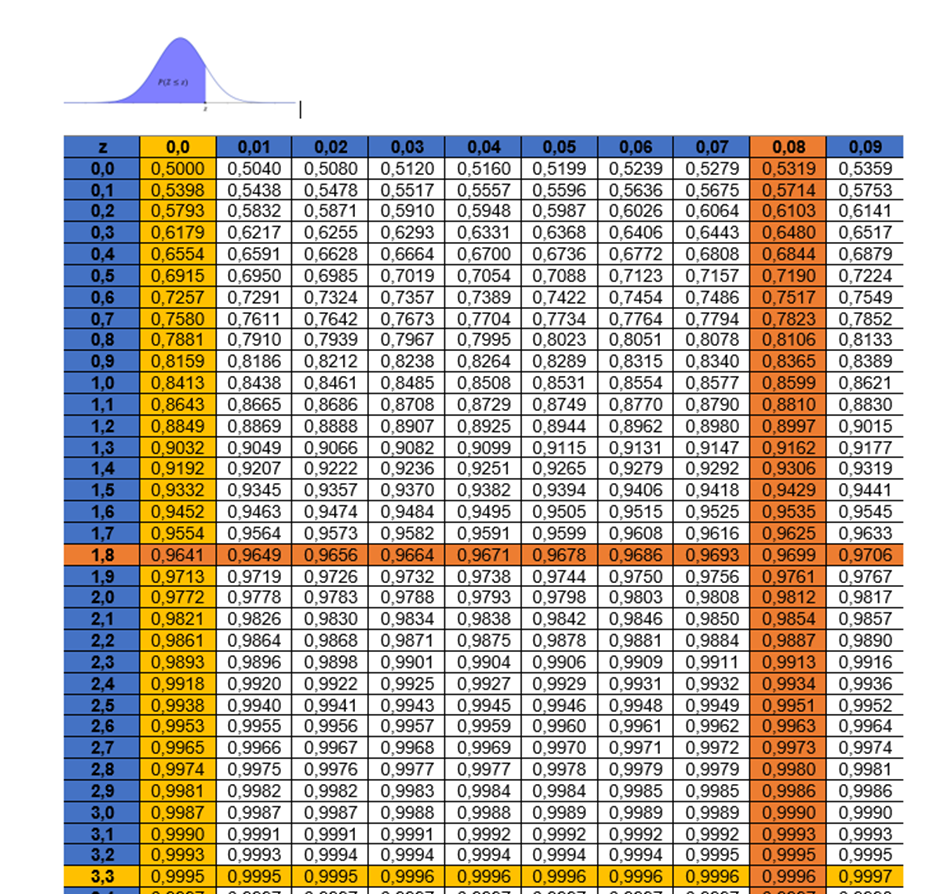
Logo, $(24,6\le x \le 25,7)=P(-1,88\le Z\le 3,30)=P(Z\le 3,30)-[1-P(Z\ge 1,88\left)\right]=0,9995-[1-0,9699]=0,9995-0,0301=0,9694$. Nesse sentido, a probabilidade de que a média de tempo que os motoristas passam dirigindo todos os dias seja entre 24,6 e 25,7 minutos é de 96,94%.

Uma técnica essencial na estatística inferencial é a estimação de parâmetros, na qual utilizamos estatísticas amostrais para calcular o valor de um parâmetro populacional desconhecido. Essas estimativas podem assumir a forma de estimadores pontuais, representando um único valor estimado para o parâmetro, ou estimadores intervalares, que consistem em um intervalo de valores usados para estimar o referido parâmetro. Vamos direcionar nosso enfoque para os estimadores intervalares, pois, ao contrário dos estimadores pontuais, que fornecem apenas um valor único como estimativa, os estimadores intervalares adotam uma abordagem mais abrangente, reconhecendo a incerteza associada à estimativa.

A proposta consiste em estabelecer um intervalo que, com um nível de confiança conhecido (denominado $1-\alpha$), englobe o valor real do parâmetro. Esse tipo de intervalo é referido como intervalo de confiança para o parâmetro. O termo nível de confiança, $1-\alpha$, é definido como “a confiança de que a estimativa intervalar contém o verdadeiro valor do parâmetro, pressupondo que o processo de estimação seja repetido em um grande número de vezes” (Larson; Farber, 2015, p. 299). Por sua vez, $\alpha$ representa o nível de significância, indicando a probabilidade de cometer um erro ao afirmar que o parâmetro em questão está naquele intervalo.

O nível de confiança $1-\alpha$ representa a região sob a curva normal padrão entre os valores críticos $-z_{1-a}$ e $z_{1-\alpha }$. Nesse contexto, os valores críticos atuam como limites, distinguindo as estatísticas amostrais consideradas prováveis daquelas que são improváveis. A Figura 3 ilustra que $1-\alpha$ corresponde à porcentagem da área sob a curva normal situada entre ${-z}_{1-\alpha }$ e $z_{1-\alpha }$. A porção restante da área é $\alpha$, sendo que a área em cada cauda será dada por $\frac{\alpha }{2}$.

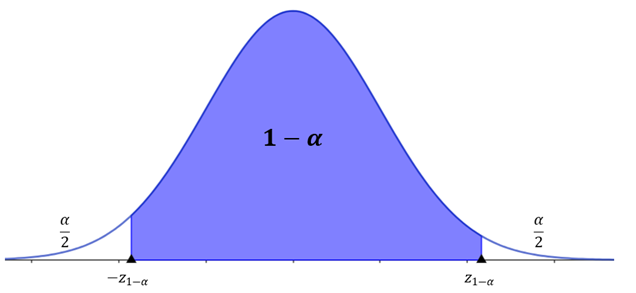
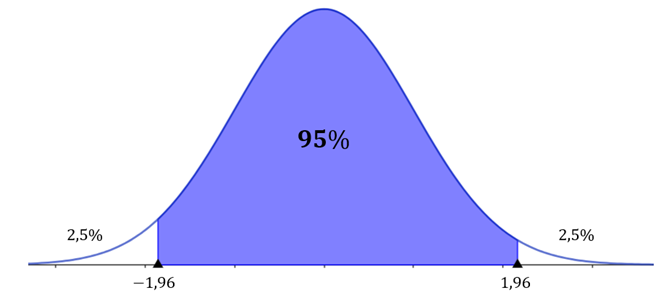
A fim de obtermos os valores críticos, é necessário consultar uma tabela da distribuição normal padrão para encontrar o z-escore correspondente à área fornecida. Por exemplo, ao considerarmos um nível de confiança de 95%, ou seja, $1-\alpha =0,95$, podemos afirmar que o nível de significância $\alpha$ é de 0,05 ou 5%. Nesse contexto, 2,5% da área encontram-se à esquerda de ${-z}_{1-\alpha }$, e 2,5% estão à direita de $z_{1-\alpha }$. É importante destacar a simetria da curva normal e o caráter cumulativo da tabela da distribuição normal padrão, que fornece a área à esquerda do z-escore. Portanto, ao determinarmos o valor de $z_{1-\alpha }$, consideramos a área à esquerda, ou seja, $1-0,025=0,975$. Assim, na tabela, procuramos o z-escore associado a essa área, conforme mostra a Tabela 2.

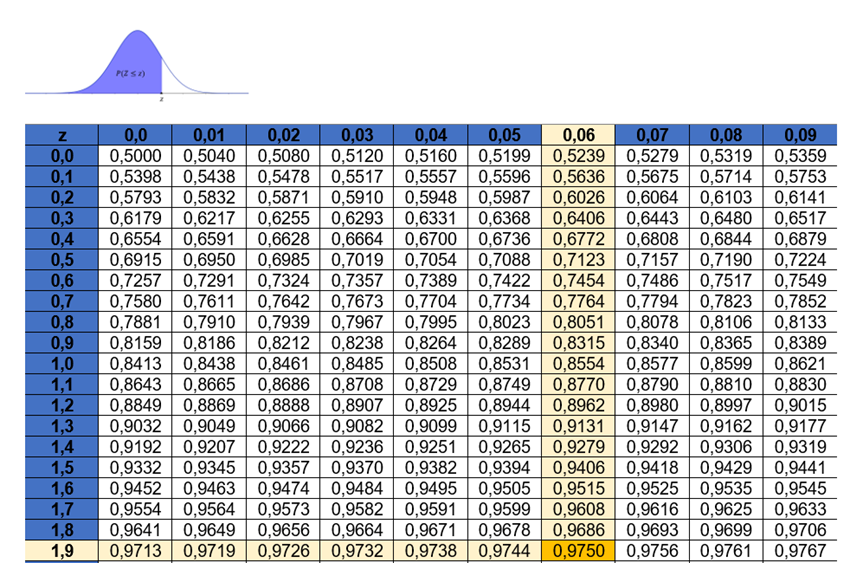
Observe que o z-escore que tem área igual a 0,9750 é 1,96. Utilizando a propriedade de simetria da curva normal, observamos que os valores críticos são ${-z}_{1-\alpha }=-1,96$ e $z_{1-\alpha }=1,96$ (Figura 4).

É normal utilizarmos os níveis de confiança de 90%, 95% e 99%. Os z-escores correspondentes a esses valores são apresentados na Tabela 3.

Nível de confiança	$z_{1-\alpha }$
90%	1,64
95%	1,96
99%	2,57

Tabela 3 | z-escore para alguns níveis de confiança. Fonte: elaborada pela autora.

 

Com base no nível de confiança, $1-\alpha$, podemos definir a margem de erro que representa a maior distância possível entre a estimativa pontual e o valor do parâmetro estimado. No caso de uma média populacional com o desvio-padrão populacional conhecido, a margem de erro é dada por:

$E=z_{1-\alpha }\cdot \frac{\sigma }{\surd n}$

Ressalta-se que a aplicação dessa fórmula para calcular o erro é viável apenas quando a amostra é aleatória e a distribuição da população é normal, ou quando $n\ge 30$. Com base no erro e em uma estimativa pontual, podemos construir um intervalo de confiança. O intervalo de confiança para a média, quando a variância populacional é conhecida, é dado por:

$IC=\overline{)x} -E<\mu <\overline{)x}+E$

Ou

$IC=\overline{)x}-z_{1-\alpha }\cdot \frac{\sigma }{\surd n}<\mu <\overline{)x}+z_{1-\alpha }\cdot \frac{\sigma }{\surd n}$

Note que, com base no tipo de erro e na estimativa pontual, podem surgir diferentes categorias de intervalos de confiança. O apresentado aqui é apenas um dos exemplos de intervalo de confiança.

 

Exemplo 2

O diretor de uma faculdade busca estimar a idade média de todos os estudantes atualmente matriculados. Em uma amostra aleatória de 30 estudantes, a idade média observada é de 22,9 anos. Com base em estudos prévios, o desvio-padrão conhecido é de 1,5 ano. Construa um intervalo de confiança de 95% para a idade média da população.

O intervalo de confiança para a média, quando a variância populacional é conhecida, é dado por:

$IC=\overline{)x}-z_{1-\alpha }\cdot \frac{\sigma }{\surd n}<\mu <\overline{)x}+z_{1-\alpha }\cdot \frac{\sigma }{\surd n}$

O problema informa que $\overline{)x}=22,9$, $\sigma =1,5$ e $n=30$. Precisamos determinar $z_{1-\alpha }$ relacionado ao nível de confiança de 95%. De acordo com a Tabela 1, $z_{1-\alpha }=1,96$ para o nível de confiança dado. Agora, basta substituirmos essas informações na expressão:

$IC=22,9-1,96\cdot \frac{1,5}{\surd 30}<\mu <22,9+1,96\cdot \frac{1,5}{\surd 30}$

$IC=22,9-1,96\cdot 0,274<\mu <22,9+1,96\cdot 0,274$

$IC=22,9-0,53704<\mu <22,9+0,53704$

$IC=22,36296<\mu <23,43704$

Logo, podemos afirmar com 95% de confiança que a idade média dos estudantes está entre 22,4 e 23,4 anos.

Vamos Exercitar?

Agora, que você já sabe como determinar um intervalo de confiança, vamos retomar nossa situação inicial. Trata-se de uma investigação referente à longevidade das baterias utilizadas em relógios de pulso, com base em uma amostra distribuída normalmente e com desvio-padrão igual a 1. Queremos determinar o intervalo de confiança para a média do tempo de duração dessas baterias, com 90% de confiança.

Observe que o problema informa que o desvio-padrão é populacional, e a amostra é aleatória e distribuída normalmente, então podemos determinar o intervalo de confiança por meio da expressão:

$IC=\overline{)x}-z_{1-\alpha }\cdot \frac{\sigma }{\surd n}<\mu <x¯+z_{1-\alpha }\cdot \frac{\sigma }{\surd n}$

O primeiro passo é determinar a média amostral. Considerando-se a amostra dada: 1,2 – 1,4 – 1,7 – 1,3 – 1,2 – 2,3 – 2,0 – 1,5 – 1,8 – 1,4 – 1,6 – 1,5 – 1,7 – 1,5 – 1,3, a média será:

$\overline{)x}=\frac{1,2+1,4+1,7+1,3+1,2+2,3+2+1,5+1,8+1,4+1,6+1,5+1,7+1,5+1,3}{15}=1,56$

De acordo com a Tabela 1, $z_{1-\alpha }=1,64$ para um nível de confiança de 90%. Agora, basta substituirmos todas as informações na expressão para calcular o intervalo de confiança:

$IC=1,56-1,64\cdot \frac{1}{\surd 15}<\mu <1,56+1,64\cdot \frac{1}{\surd 15}$

$IC=1,56-1,64\cdot 0,26<\mu <1,56+1,64\cdot 0,26$

$IC=1,56-0,43<\mu <1,56+0,43$

$IC=1,13<\mu <1,99$

Portanto, ao nível de confiança de 90% podemos afirmar que a longevidade das baterias está entre 1,13 e 1,99 ano.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre o teorema do limite central, sugerimos a leitura da seção 1.3 do livro Inferência estatística: como estabelecer conclusões com confiança no giro do PDCA e DMAIC.
Para que você possa resolver exercícios relacionados ao conceito de intervalo de confiança, sugerimos a leitura da seção 15.3 do livro Estatística. Ao final, selecione alguns exercícios e os resolva! 

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023.

WERKEMA, C. Inferência estatística: como estabelecer conclusões com confiança no giro do PDCA e DMAIC. Rio de Janeiro: Grupo GEN, 2014. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788595152328/. Acesso em: 10 nov. 2023.

Teste de hipótese para a média de uma população

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Anteriormente, você aprendeu sobre o Teorema do Limite Central (TLC) e suas implicações. Esse teorema desempenha um papel crucial na estatística inferencial e pode ser aplicado em várias situações; uma delas é o teste estatístico de hipóteses. Trata-se de um procedimento estatístico utilizado para tomar decisões ou fazer inferências sobre uma população com base em uma amostra de dados. Ele envolve a formulação de duas hipóteses opostas: a hipótese nula (H₀) e a hipótese alternativa (H₁). O resultado do teste ajuda a determinar se há evidências estatísticas suficientes para rejeitar a hipótese nula em favor da hipótese alternativa.

Os testes de hipótese são comumente usados em pesquisas científicas, experimentos, estudos clínicos e várias áreas em que os pesquisadores desejam fazer inferências sobre populações com base em amostras limitadas de dados.

Nesta aula, estudaremos o teste de hipótese para média de uma amostra com a variância populacional conhecida. Para entender como podemos aplicar esse conceito, considere que determinada máquina é responsável por cortar barras de metal, com comprimento médio de 50 centímetros, sendo a variável $X$ distribuída como $X ~ (\mu ,25 cm)$. Caso a média dos comprimentos seja diferente de 50 centímetros, a empresa enfrentará prejuízo. Alguns funcionários têm suspeitas de que a máquina está desregulada. Para verificarem essa suspeita, eles realizaram uma amostragem de tamanho $n = 36$ e obtiveram uma média amostral de $\mathrm{x̅} = 52 cm$. Com um nível de significância de 5%, há indícios suficientes para confirmar a suspeita dos funcionários?

Para responder a essa pergunta, é fundamental compreender o que é um teste de hipótese, bem como os procedimentos envolvidos em sua execução.

Bons estudos!

Vamos Começar!

Os testes estatísticos de hipóteses constituem técnicas utilizadas na inferência estatística. Em outras palavras, ao conduzir um teste de hipóteses com dados amostrais, é possível realizar inferências sobre a população. O processo básico de um teste estatístico envolve a formulação de uma hipótese em relação ao valor de um parâmetro. Utilizando os elementos amostrais e as técnicas estatísticas, conclui-se pela aceitação ou rejeição da hipótese formulada.

Uma afirmação relativa a um parâmetro é denominada hipótese estatística. Ao testar um parâmetro, é crucial definir de forma precisa um par de hipóteses: uma que expresse a proposição e outra que expresse sua negação. Quando uma dessas hipóteses é falsa, a outra deve ser verdadeira (Larson; Farber, 2015). Denominamos essas hipóteses nula e alternativa. A hipótese nula, H₀, é uma hipótese estatística que contém uma informação de igualdade como $=,\ge$ou $\le$.

Por outro lado, a hipótese alternativa, H₁, é o complemento da hipótese nula e deve conter uma desigualdade estrita, tal como $\ne ,<$ou$>$.

A hipótese alternativa é verdadeira quando H₀ é falsa.

Independentemente de qual das hipóteses represente a afirmação, em um teste de hipóteses, sempre se inicia assumindo que a condição de igualdade na hipótese nula é verdadeira. Durante a realização de um teste de hipóteses, uma das duas decisões é tomada:

1. Rejeitar a hipótese nula.
2. Não rejeitar a hipótese nula.

Devido ao fato de que a decisão é pautada em uma amostra, e não na população inteira, existe sempre a possibilidade de tomar uma decisão incorreta (Larson; Farber, 2015). Em relação à nossa decisão de aceitar ou rejeitar H₀, podemos ter quatro resultados (Tabela 1).

	Veracidade de H0
Decisão	H0 é verdadeira	H0 é falsa
Não rejeita H0	Decisão correta	Erro do tipo II
Rejeita H0	Erro do tipo I	Decisão correta

Tabela 1 | Resultados possíveis de um teste de hipóteses. Fonte: Larson e Farber (2015, p. 351).

 

Dependendo do tipo de parâmetro que examinamos, podemos empregar distintos tipos de testes. Nesse contexto, nosso interesse se concentra nos testes relacionados à média de uma população. Inicialmente, concentraremos nosso estudo na execução de um teste para a média quando a variância populacional é conhecida. A seguir, observe o passo a passo de como realizar esse tipo de teste.

 

1º Passo: formular as hipóteses

Já estudamos que um teste de hipótese é composto de dois tipos de hipóteses: uma hipótese nula e uma hipótese alternativa.

Ao formular as hipóteses nula e alternativa, é necessário expressar a proposição relativa ao parâmetro como uma sentença matemática e, em seguida, redigir sua negação. Por exemplo, se a alegação sobre o parâmetro é representada por $r$ e o parâmetro populacional é $\mu$, alguns pares possíveis incluem:

$\left\{\begin{array}{c}{H}_0:\mu =r\\ H_1:\mu \ne r\end{array}\right.$          $\left\{\begin{array}{c}{H}_0:\mu =r\\ H_1:\mu >r\end{array}\right.$              $\left\{\begin{array}{c}{H}_0:\mu =r\\ H_1:\mu <r\end{array}\right.$            $\left\{\begin{array}{c}{H}_0:\mu \ge r\\ H_1:\mu <r\end{array}\right.$           $\left\{\begin{array}{c}{H}_0:\mu \le r\\ H_1:\mu >r\end{array}\right.$

2º Passo: nível de significância de um teste

É a probabilidade máxima de rejeitar a hipótese nula, $H_0$. Por exemplo, ao utilizar um nível de significância  de 5%, $H_0$ que incorreríamos em erro ao rejeitá-la com uma probabilidade máxima de 0,05%. Geralmente realizamos testes de hipótese com nível de significância de 2%, 5% ou 10%.

 

3º Passo: definição da região crítica

A região em que os valores das estatísticas de teste conduzem à rejeição da hipótese nula é denominada região crítica (RC). Sua extensão é equivalente ao nível de significância, e sua orientação segue a mesma direção da hipótese alternativa. Assim, considerando o tipo de hipótese alternativa, podemos ter três tipos de regiões: unilateral à direita, unilateral à esquerda e bilateral.

A Figura 1 ilustra a região crítica para um teste bilateral.

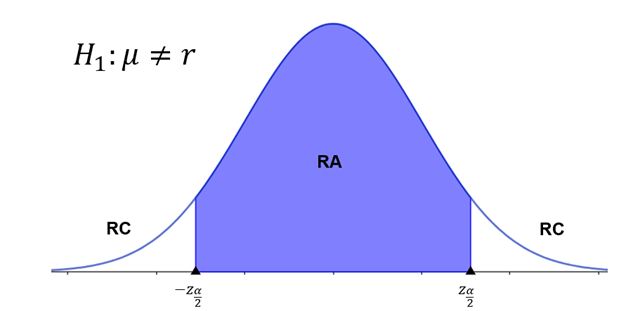
Para determinarmos a região crítica nesse caso, primeiro temos que dividir o nível de significância $\left(\alpha \right)$ igualmente entre as duas caudas da distribuição. Isso geralmente resulta em dois valores críticos, um para cada extremidade. Utilizando uma tabela da distribuição normal padrão, podemos encontrar os valores críticos correspondentes ao nível de significância dividido por 2 em cada extremidade. Por exemplo, se o nível de significância é 5%, 2,5% da área encontram-se à esquerda de $-z_{\frac{\alpha }{2}}$, e 2,5% estão à direita de $z_{\frac{\alpha }{2}}$. Ao determinarmos o valor de , consideramos a área à esquerda, ou seja, $1-\mathrm{0,025}=\mathrm{0,975}$ Assim, na tabela, procuramos o z-escore associado a esse valor, que é $z=\mathrm{1,96}$.

A Figura 2 ilustra a região crítica para um teste unilateral à esquerda.

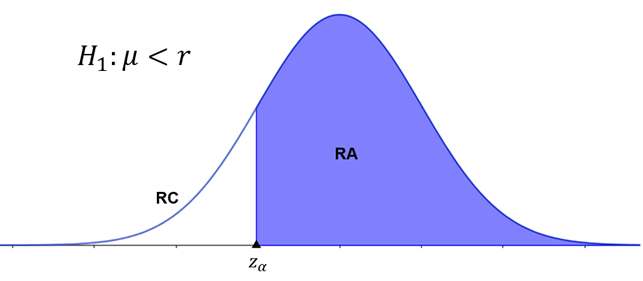
Observe que, ao adotarmos uma hipótese alternativa do tipo “menor que”, a área crítica se encontra na cauda esquerda da distribuição. Nesse cenário, é suficiente determinar o z-escore associado à área dessa cauda. Por exemplo, considere um teste unilateral à esquerda com um nível de significância de 10%. Precisamos identificar o valor de z cuja área à esquerda é 0,1. Nota-se que 0,1 corresponde à área da região crítica. A Tabela 2 mostra que o z-escore cuja área é aproximadamente 0,10 é $z_{\alpha }=-\mathrm{1,28}$.

A Figura 3 ilustra a região crítica para um teste unilateral à direita.

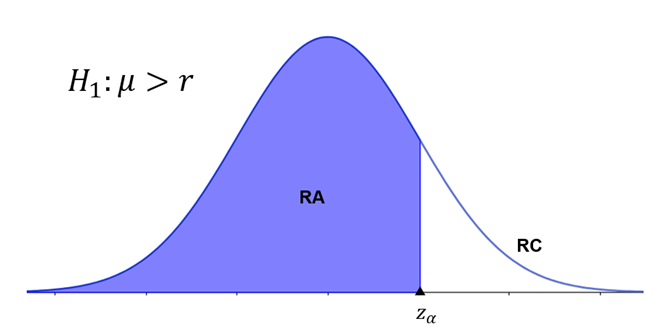
Ao adotarmos uma hipótese alternativa do tipo “maior que”, a região crítica se encontra à direita da distribuição. Assim, para determinarmos o z-escore referente a essa área crítica, fazemos $1-\alpha$ e encontramos a área à esquerda do z-escore. Por exemplo, considere um teste unilateral à esquerda com um nível de significância de 5%. Precisamos identificar o valor de z cuja área à esquerda é $1-\mathrm{0,05}=\mathrm{0,95}$, e esse valor é $z_{\alpha }=\mathrm{1,64}$.

 

4º Passo: calcular a estatística do teste

Como o objetivo é testar a média populacional da variável  $X~ N (\mu ,{\sigma }^2)$, pelo teorema do limite central sabemos que a média amostral tem comportamento aproximadamente normal da forma que $\stackrel{-}{x}~N\left(\mu ,\frac{{\sigma }^2}{n}\right)$ caso a hipótese nula seja verdadeira. A estatística do teste é o valor derivado da amostra que orientará o processo de decisão. Esse valor é calculado como $Z_{calc}$ (ou Z calculado) representado simplesmente por $Z$. O cálculo é realizado da seguinte maneira:

$z=\frac{\stackrel{-}{x}-\mu }{\frac{\sigma }{\sqrt{n}}}$

Em que

$\mu =$média populacional.

$\sigma =$desvio-padrão populacional.

$\stackrel{-}{x}=$média amostral da variável.

 

5º Passo: tomar a decisão

Se o valor encontrado para $Z_{calc}$, que é o valor calculado com base na amostra utilizada na decisão. Se $Z_{c}alc<$$Z_{tab}$ (em uma distribuição unilateral à esquerda), $Z_{calc}>$ ou $Z_{tab}$ (em uma distribuição unilateral à direita), ou $Z_{calc}\ne$$Z_{tab}$ então rejeitamos a hipótese nula. Em outras palavras, há evidências significativas de que a média populacional difere do valor indicado em H₀.

Siga em Frente...

Com base nesse passo a passo, vamos resolver o exemplo a seguir.

 

Exemplo

Vamos considerar que uma indústria adquire parafusos de determinado fabricante, e a carga média de ruptura por tração especificada é de 50 quilos, com um desvio-padrão das cargas de ruptura igual a 4 quilos. O comprador realiza uma amostragem de 30 parafusos e encontra uma média de ruptura de 49 quilos. Com um nível de significância de 5%, há evidências que apoiem a suspeita do comprador de que a carga média de ruptura dos parafusos seja inferior a 50 quilos?

• 1º Passo: formular as hipóteses

$H_0:\mu =50$

$H_1:\mu <50$

• 2º Passo: nível de significância de um teste

O nível de significância foi informado como $\alpha =5\%$.

•  3º Passo: definição da região crítica

Nossa hipótese alternativa é do tipo “menor que”, logo temos um teste unilateral à esquerda. A área crítica se encontra na cauda esquerda da distribuição, assim é suficiente determinar o z-escore associado à área dessa cauda. Como temos um nível de significância de 5%, precisamos identificar o valor de z cuja área à esquerda é 0,05, e esse valor é $z=-\mathrm{1,64}$, conforme ilustra a Tabela 3.

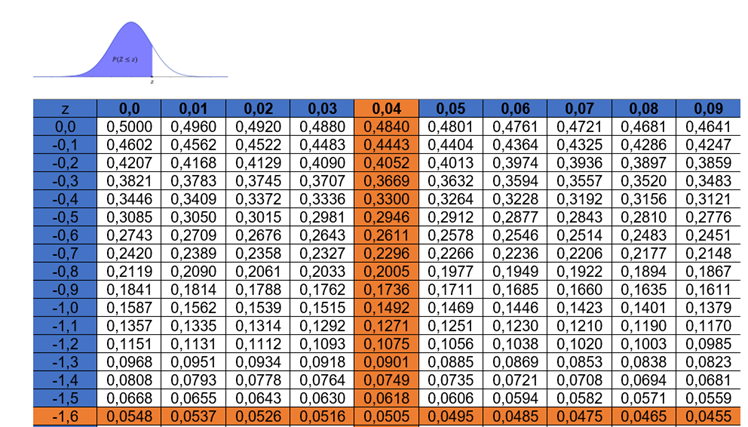
Assim, temos a região crítica conforme a Figura 4.

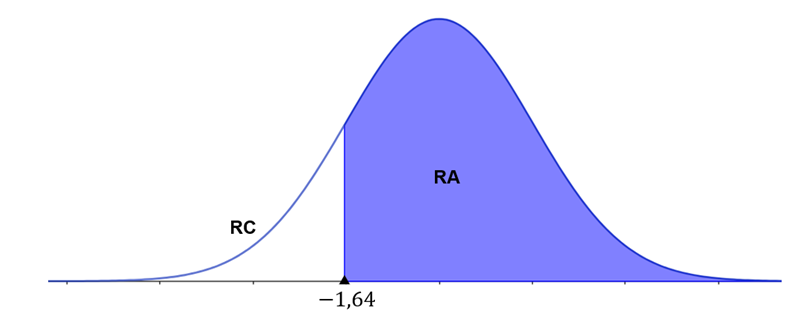
• 4º Passo: calcular a estatística com base na amostra

Como o objetivo é testar a média populacional da variável $X~ N (\mu ,{\sigma }^2)$, pelo teorema do limite central sabemos que a média amostral tem comportamento aproximadamente normal da forma $\stackrel{-}{x}~N\left(50,\frac{4^2}{30}\right)$, ou seja, $x ̅~N(50;0,53)$. $Z_{calc}$ (ou Z calculado), será dado por:

$z=\frac{\stackrel{-}{x}-\mu }{\frac{\sigma }{\sqrt{n}}}$

$z=\frac{49-50}{\frac{4}{\sqrt{30}}}=-\mathrm{1,36}$

• 5º Passo: tomar a decisão

Temos que $Z_{calc}>Z_{tab}$, ou seja, $Z_{calc}$ encontra-se na região de aceitação, logo podemos aceitar a hipótese nula. Isso significa que não há evidências que apoiem a suspeita do comprador de que a carga média de ruptura dos parafusos seja inferior a 50 quilos.

Vamos Exercitar?

Agora, que você já sabe todos os procedimentos para realizar um teste de hipótese para média populacional quando a variância populacional é conhecida, vamos retornar à nossa situação inicial. Nela, consideramos que determinada máquina é responsável por cortar barras de metal, com comprimento médio de 50 centímetros, sendo a variável $X$ distribuída como $X ~ (\mu , 25 cm)$.

Sabemos que se a média dos comprimentos for diferente de 50 centímetros, a empresa enfrentará prejuízo e que alguns funcionários têm suspeitas de que a máquina esteja desregulada. Para verificar isso, eles realizaram uma amostragem de tamanho $n = 36$e obtiveram uma média amostral de $\overline{)x} = 52 cm$. Nós devemos verificar se, com um nível de significância de 5%, há indícios suficientes para confirmar a suspeita dos funcionários. Vamos seguir os passos elencados anteriormente para realizar o teste de hipótese.

• 1º Passo: formular as hipóteses

Sabemos que se a média dos comprimentos for diferente de 50 centímetros, há prejuízos. Assim, nossas hipóteses serão:

$H_0:\mu =50$

$H_1:\mu \ne 50$

• 2º Passo: nível de significância de um teste

O nível de significância foi informado como $\alpha =5\%$.

• 3º Passo: definição da região crítica

Nossa hipótese alternativa é do tipo “diferente”, portanto é um teste bilateral. Para determinarmos a região crítica nesse caso, primeiro temos que dividir o nível de significância $\left(\alpha \right)$ igualmente entre as duas caudas da distribuição. Nosso nível de significância é de 5%, ou seja, 2,5% da área encontram-se à esquerda de $-z_{\frac{\alpha }{2}}$, e 2,5% estão à direita de $z_{\frac{\alpha }{2}}$. Ao determinarmos o valor de $z_{\frac{\alpha }{2}}$, consideramos a área à esquerda, ou seja, $1-\mathrm{0,025}=\mathrm{0,975}$. Assim, na tabela, procuramos o z-escore associado a esse valor, que é $z=\mathrm{1,96}$. Logo, nossa região crítica será conforme a Figura 5.

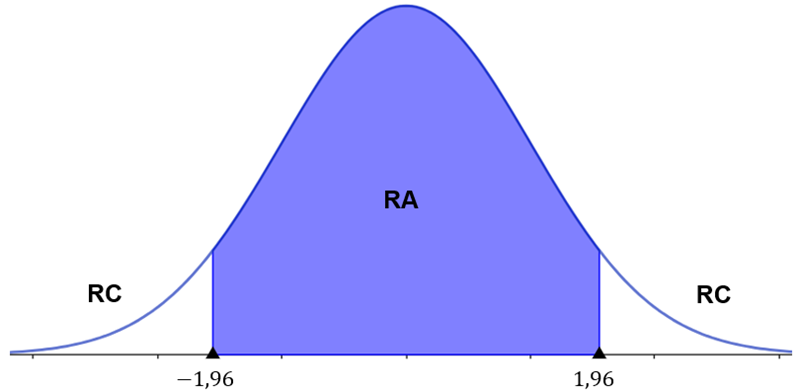
• 4º Passo: calcular a estatística com base na amostra

Como o objetivo é testar a média populacional da variável $X~ N (\mu ,25)$, pelo teorema do limite central sabemos que a média amostral tem comportamento aproximadamente normal da forma $\stackrel{-}{x}~N\left(50,\frac{25}{36}\right)$, ou seja, $\stackrel{-}{x}~N\left(50;\mathrm{0,69}\right)$.

Considerando que a variância populacional é 25, lembre-se de que o desvio-padrão será a raiz quadrada da variância; assim, $Z_{calc}$ (ou Z calculado) será dado por:

$z=\frac{\stackrel{-}{x}-\mu }{\frac{\sigma }{\sqrt{n}}}$

$z=\frac{52-50}{\frac{\sqrt{25}}{\sqrt{36}}}=\mathrm{2,4}$

•  5º Passo: tomar a decisão

Sabemos que $Z_{calc}>Z_{tab}$, ou seja, $Z_{calc}$ encontra-se na região crítica, logo rejeitamos a hipótese nula. Assim, em um nível de significância de 5%, há indícios estatísticos para confirmar a suspeita dos funcionários em relação à média dos comprimentos (que é diferente de 50 centímetros) e, consequentemente, à possibilidade de prejuízo para a empresa.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre o teste de hipótese, sugerimos a leitura das seções 7.1 e 7.2 do livro Estatística aplicada. Em seguida, escolha alguns exercícios para resolver!

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023.

Outro teste de hipótese para a média de uma população

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Você já se familiarizou com a execução de um teste de hipótese para a média quando a variância populacional é conhecida. No entanto, surge uma situação distinta quando apenas a variância amostral é conhecida e a amostra contém menos de 30 elementos. Nesse caso, utilizamos a distribuição t de Student para realizar o teste de hipótese.

Nesta aula, exploraremos as propriedades relacionadas à distribuição t de Student e executaremos testes de hipóteses para média quando a variância populacional é desconhecida. Para entender como podemos aplicar esse conceito, considere que uma máquina é projetada para cortar barras de metal com um comprimento médio de 50 centímetros, sendo o comprimento dessas barras uma variável aleatória $X$ com distribuição .$X~(\mu , {\sigma }^2)$ Se a média dos comprimentos for maior de 50 cm, isso representa prejuízo para a empresa. Suspeitando que a máquina pode estar desregulada e causando prejuízo, alguns funcionários decidiram investigar. Eles coletaram uma amostra de tamanho $n=28$e encontraram uma média amostral $\overline{)x}=52,04$cm e uma variância amostral $S^2=25$ cm². Com um nível de significância de 5%, há indícios suficientes para confirmar a suspeita dos funcionários?

Para responder a essa pergunta, é fundamental compreender como podemos realizar um teste de hipótese para média quando a variância populacional é desconhecida.

Bons estudos!

Vamos Começar!

A distribuição t de Student é um modelo de probabilidade desenvolvido pelo químico britânico W.S. Gosset, que publicou seus trabalhos, em 1908, sob o pseudônimo “Student”. Gosset trabalhava em uma cervejaria e aparentemente não desejava que seus concorrentes descobrissem que sua equipe de profissionais estava utilizando técnicas estatísticas para o aprimoramento de seus processos produtivos (Werkema, 2014).

A distribuição t surgiu da necessidade de lidar com a incerteza introduzida ao estimar a variância de uma população com base em uma amostra pequena. Enquanto a distribuição normal é usada quando a variância populacional é conhecida, a distribuição t é mais apropriada quando a variância populacional é desconhecida e precisa ser estimada com base nos dados da amostra.

A estatística t, com $n-1$ graus de liberdade, é denotada por:

$\mathit{t}=\frac{\stackrel{-}{\mathit{x}}-\mathit{\mu }}{\sqrt{\frac{{\mathit{S}}^2}{\mathit{n}}}}$

Em que $S^2$ é a variância amostral. 

A necessidade de utilizar a qualificação com $n-1$ graus de liberdade advém do fato de que, para cada valor distinto do tamanho da amostra $n$(ou, de forma equivalente, para cada valor distinto de $n-1$), existe uma distribuição t específica. A distribuição t é contínua e simétrica, com uma média de zero. Sua aparência é semelhante à da distribuição normal padronizada, mas a distribuição t exibe uma maior variabilidade. Essa variabilidade adicional, em comparação com a distribuição normal padrão, é o resultado da substituição de  por  no denominador do quociente $z=\frac{\stackrel{-}{x}-\mu }{\frac{\sigma }{\sqrt{n}}}$ (Werkema, 2014).

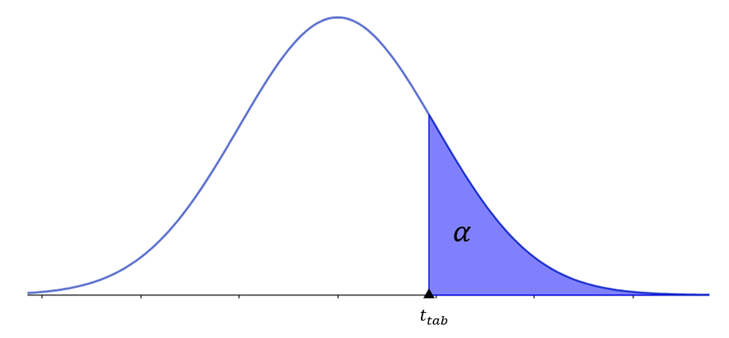
Ao contrário da distribuição z, que tem uma única tabela abrangente, a distribuição t exigiria uma variedade considerável de tabelas, uma para cada grau de liberdade. No entanto, para nosso propósito, não é necessário ter uma tabela tão abrangente quanto a tabela Z. Uma tabela que inclua probabilidades-chave, amplamente utilizadas, é suficiente, conforme ilustrado na Tabela 1. Seu cabeçalho apresenta os níveis de significância. A coluna à esquerda lista os graus de liberdade, enquanto o corpo da tabela fornece os valores de $t_{tab}$ (t tabelado). A Figura 1 ilustra área à qual a Tabela 1 se refere.

Grau de liberdade	Nível de significância  unilateral
	0,1%	0,2%	0,5%	1%	2%	2,5%	5%
1	318,309	159,153	63,657	31,821	15,895	12,706	6,314
2	22,327	15,764	9,925	6,965	4,849	4,303	2,920
3	10,215	8,053	5,841	4,541	3,482	3,182	2,353
4	7,173	5,951	4,604	3,747	2,999	2,776	2,132
5	5,893	5,030	4,032	3,365	2,757	2,571	2,015
6	5,208	4,524	3,707	3,143	2,612	2,447	1,943
7	4,785	4,207	3,499	2,998	2,517	2,365	1,895
8	4,501	3,991	3,355	2,896	2,449	2,306	1,860
9	4,297	3,835	3,250	2,821	2,398	2,262	1,833
10	4,144	3,716	3,169	2,764	2,359	2,228	1,812
11	4,025	3,624	3,106	2,718	2,328	2,201	1,796
12	3,930	3,550	3,055	2,681	2,303	2,179	1,782
13	3,852	3,489	3,012	2,650	2,282	2,160	1,771
14	3,787	3,438	2,977	2,624	2,264	2,145	1,761
15	3,733	3,395	2,947	2,602	2,249	2,131	1,753
16	3,686	3,358	2,921	2,583	2,235	2,120	1,746
17	3,646	3,326	2,898	2,567	2,224	2,110	1,740
18	3,610	3,298	2,878	2,552	2,214	2,101	1,734
19	3,579	3,273	2,861	2,539	2,205	2,093	1,729
20	3,552	3,251	2,845	2,528	2,197	2,086	1,725
21	3,527	3,231	2,831	2,518	2,189	2,080	1,721
22	3,505	3,214	2,819	2,508	2,183	2,074	1,717
23	3,485	3,198	2,807	2,500	2,177	2,069	1,714
24	3,467	3,183	2,797	2,492	2,172	2,064	1,711
25	3,450	3,170	2,787	2,485	2,167	2,060	1,708
26	3,435	3,158	2,779	2,479	2,162	2,056	1,706
27	3,421	3,147	2,771	2,473	2,158	2,052	1,703
28	3,408	3,136	2,763	2,467	2,154	2,048	1,701
29	3,396	3,127	2,756	2,462	2,150	2,045	1,699
30	3,385	3,118	2,750	2,457	2,147	2,042	1,697

Tabela 1 | Distribuição t de Student (unilateral). Fonte: elaborada pela autora.

 

 

O passo a passo para realizar o teste de hipótese para média quando a variância populacional é desconhecida é análogo ao teste quando a variância populacional é conhecida. A seguir, observe o passo a passo de como realizar o teste.

1º Passo: formular as hipóteses

Sabemos que um teste de hipótese é composto de dois tipos de hipóteses: uma hipótese nula e uma hipótese alternativa. Se considerarmos que a alegação sobre o parâmetro é representada por $r$ e o parâmetro populacional é $\mu$, temos as seguintes possibilidades de hipóteses:

$\left\{\begin{array}{c}{H}_0:\mu =r\\ H_1:\mu \ne r\end{array}\right.$         $\left\{\begin{array}{c}{H}_0:\mu =r\\ H_1:\mu >r\end{array}\right.$        $\left\{\begin{array}{c}{H}_0:\mu =r\\ H_1:\mu <r\end{array}\right.$        $\left\{\begin{array}{c}{H}_0:\mu \ge r\\ H_1:\mu <r\end{array}\right.$        $\left\{\begin{array}{c}{H}_0:\mu \le r\\ H_1:\mu >r\end{array}\right.$

• 2º Passo: nível de significância de um teste

É a probabilidade máxima de rejeitar a hipótese nula, $H_0$. Geralmente realizamos testes de hipótese com nível de significância $\alpha$ de 2%, 5% ou 10%.

• 3º Passo: definição dos graus de liberdade $\left(v\right)$

É o número de desvios em relação à média que não estão relacionados entre si. Para calcular os graus de liberdade, efetuamos $v = n – 1$.

• 4º Passo: definição da região crítica

A zona em que os valores das estatísticas de teste levam à rejeição da hipótese nula é chamada de região crítica (RC). Dependendo do tipo de hipótese alternativa, existem três categorias de regiões: unilateral à direita, unilateral à esquerda e bilateral.

Para determinar os valores críticos que delimitam a região crítica em um teste bilateral, primeiro temos que dividir o nível de significância $\left(\alpha \right)$ igualmente entre as duas caudas da distribuição (Figura 2).

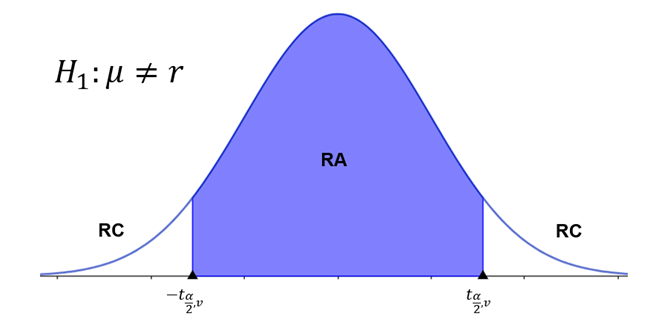
Utilizando uma tabela da distribuição t de Student, podemos encontrar os valores críticos correspondentes ao nível de significância, dividido por 2 em cada extremidade, considerando os $n-1$graus de liberdade. Por exemplo, suponhamos que estejamos conduzindo um teste bilateral com um nível de significância de 10% usando uma amostra de 20 elementos. O valor $t_{\frac{\alpha }{2},v}$ é encontrado na interseção entre a coluna correspondente ao nível de significância de 5%, uma vez que precisamos dividir pela metade o nível de significância fornecido e a linha dos graus de liberdade $v=n-1\to 20-1=19$. Assim, temos que $t_{\frac{\alpha }{2},v}=\mathrm{1,729}$, conforme ilustra a Tabela 2.

Grau de liberdade	Nível de significância   unilateral
	0,1%	0,2%	0,5%	1%	2%	2,5%	5%
1	318,309	159,153	63,657	31,821	15,895	12,706	6,314
2	22,327	15,764	9,925	6,965	4,849	4,303	2,920
3	10,215	8,053	5,841	4,541	3,482	3,182	2,353
4	7,173	5,951	4,604	3,747	2,999	2,776	2,132
5	5,893	5,030	4,032	3,365	2,757	2,571	2,015
6	5,208	4,524	3,707	3,143	2,612	2,447	1,943
7	4,785	4,207	3,499	2,998	2,517	2,365	1,895
8	4,501	3,991	3,355	2,896	2,449	2,306	1,860
9	4,297	3,835	3,250	2,821	2,398	2,262	1,833
10	4,144	3,716	3,169	2,764	2,359	2,228	1,812
11	4,025	3,624	3,106	2,718	2,328	2,201	1,796
12	3,930	3,550	3,055	2,681	2,303	2,179	1,782
13	3,852	3,489	3,012	2,650	2,282	2,160	1,771
14	3,787	3,438	2,977	2,624	2,264	2,145	1,761
15	3,733	3,395	2,947	2,602	2,249	2,131	1,753
16	3,686	3,358	2,921	2,583	2,235	2,120	1,746
17	3,646	3,326	2,898	2,567	2,224	2,110	1,740
18	3,610	3,298	2,878	2,552	2,214	2,101	1,734
19	3,579	3,273	2,861	2,539	2,205	2,093	1,729

Tabela 2 | Distribuição t de Student (unilateral). Fonte: elaborada pela autora.

 

Para determinar o limite da região crítica quando o teste é unilateral, basta identificar o nível de significância e o grau de liberdade correspondente na tabela.

• 5º Passo: calcular a estatística do teste

A estatística do teste t, com $n-1$ graus de liberdade, é denotada por:

${\mathit{t}}_{\mathit{c}\mathit{a}\mathit{l}\mathit{c}}=\mathit{t}=\frac{\stackrel{-}{\mathit{x}}-\mathit{\mu }}{\sqrt{\frac{{\mathit{S}}^2}{\mathit{n}}}}$

Em que $S^2$ é a variância amostral. 

• 6º Passo: tomar a decisão

Se o valor encontrado para $t_{calc}$ estiver na região de aceitação, aceite H₀. Se $t_{calc}$ estiver na região de rejeição, rejeite H₀.

Uma abordagem alternativa para a tomada de decisão é a comparação entre o valor tabelado de t (chamado de $t_{tab}$) e $t_{calc}$, o valor calculado com base na amostra utilizada na decisão. Se $t_{c}alc<$$t_{tab}$(em uma distribuição unilateral à esquerda), ou $t_{calc}>$$t_{tab}$ (em uma distribuição unilateral à direita), ou $t_{calc}\ne$$t_{tab}$então rejeitamos a hipótese nula. Em outras palavras, há evidências significativas de que a média populacional difere do valor indicado em H₀.

Siga em Frente...

Com base nesse passo a passo, vamos resolver o exemplo a seguir.

 

Exemplo

Em indivíduos sadios, o consumo renal de oxigênio distribui-se normalmente em torno de $12 c{m}^3/min$. Deseja-se investigar, com base em cinco indivíduos portadores de certa moléstia, se esta tem influência no consumo renal médio de oxigênio. Sabendo que o consumo médio é  e a variância é de , qual é a conclusão, ao nível de 1% de significância?

• 1º Passo: formular as hipóteses

$H_0:\mu =12$

$H_1:\mu \ne 12$

• 2º Passo: nível de significância de um teste

O nível de significância foi informado como $\alpha =1\%.$

• 3º Passo: definição dos graus de liberdade $\left(\mathit{v}\right)$

Grau de liberdade $v=n-1\to v=5-1=4$

• 4º Passo: definição da região crítica

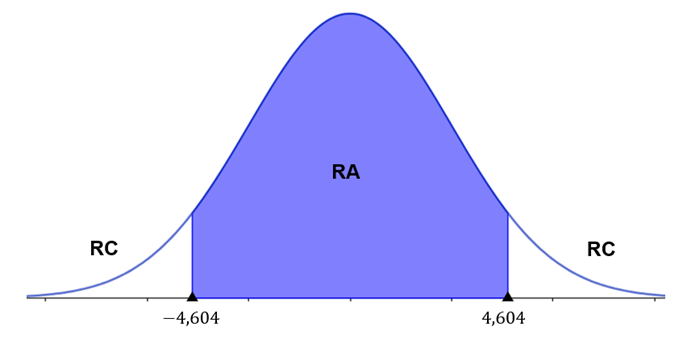
Nossa hipótese alternativa é do tipo “diferente”, então temos um teste bilateral. Para determinarmos os limites da região de aceitação, precisamos dividir o nível de significância por dois. Assim, na tabela, devemos buscar a interseção entre a coluna correspondente ao nível de significância de 0,5% e a linha dos graus de liberdade $v=4$. Então, temos que $t_{\frac{\alpha }{2},v}=\mathrm{4,604}$, conforme ilustra a Tabela 3.

Grau de liberdade	Nível de significância $\left(\alpha \right)$ unilateral
	0,1%	0,2%	0,5%	1%	2%	2,5%	5%
1	318,309	159,153	63,657	31,821	15,895	12,706	6,314
2	22,327	15,764	9,925	6,965	4,849	4,303	2,920
3	10,215	8,053	5,841	4,541	3,482	3,182	2,353
4	7,173	5,951	4,604	3,747	2,999	2,776	2,132
5	5,893	5,030	4,032	3,365	2,757	2,571	2,015
6	5,208	4,524	3,707	3,143	2,612	2,447	1,943
7	4,785	4,207	3,499	2,998	2,517	2,365	1,895

Tabela 3 | Distribuição t de Student (unilateral). Fonte: elaborada pela autora.

 

A Figura 3 ilustra a região crítica.

• 5º Passo: calcular a estatística do teste

A estatística do teste t, com  graus de liberdade, é denotada por:

$t_{calc}=t=\frac{\stackrel{-}{x}-\mu }{\sqrt{\frac{S^2}{n}}}$

$t_{calc}=\frac{\mathrm{13,90}-12}{\frac{\sqrt{\mathrm{0,665}}}{\sqrt{5}}}\approx \mathrm{5,21}$

• 6º Passo: tomar a decisão

Temos que $t_{calc}>t_{tab}$, ou seja, $t_{calc}$ encontra-se na região crítica, logo rejeitamos $H_0$. Portanto, podemos concluir que a evidência amostral indica, ao nível de 1% de significância, que a referida moléstia tem influência no consumo renal médio de oxigênio.

Ao realizar um teste de hipótese, é crucial atentar-se para a formulação da hipótese alternativa, pois ela orientará qual será o tipo de região crítica (unilateral ou bilateral). Adicionalmente, a interpretação dos resultados é fundamental, visto que é preciso explicitar o significado de aceitar ou rejeitar a hipótese nula.

Vamos Exercitar?

Agora, que você já sabe todos os procedimentos para realizar um teste de hipótese para média populacional quando a variância populacional é desconhecida, vamos retomar nossa situação inicial. Nela, consideramos que determinada máquina é responsável por cortar barras de metal, com um comprimento médio de 50 centímetros, sendo a variável $X$ com distribuição $X~(\mu , {\sigma }^2)$.

Sabemos que se a média dos comprimentos for maior de 50 centímetros, isso representa prejuízo para a empresa. Suspeitando que a máquina pode estar desregulada e causando prejuízo, alguns funcionários decidiram investigar. Eles coletaram uma amostra de tamanho $n=28$ e encontraram uma média amostral $\stackrel{-}{x}=\mathrm{52,04}$ cm e uma variância amostral $S^2=25$cm². Considerando um nível de significância de 5%, temos que verificar se há indícios suficientes para confirmar a suspeita dos funcionários.

Vamos seguir os passos elencados anteriormente para realizar o teste de hipótese.

• 1º Passo: formular as hipóteses

Sabemos que se a média dos comprimentos for maior que 50 centímetros, há prejuízos. Assim, nossas hipóteses são:

$H_0:\mu =50$

$H_1:\mu >50$

• 2º Passo: nível de significância de um teste

O nível de significância foi informado como $\alpha =5\%$.

• 3º Passo: definição dos graus de liberdade $\left(\mathit{v}\right)$

Como temos uma amostra de 28 elementos, o grau de liberdade é $v=n-1\to v=28-1=27$.

• 4º Passo: definição da região crítica

Como temos uma hipótese alternativa do tipo “maior que”, trata-se de um teste unilateral à direita. Na tabela, buscaremos a interseção entre a coluna correspondente ao nível de significância de 5% e a linha dos graus de liberdade $v=27$, conforme ilustra a Tabela 4.

Grau de liberdade	Nível de significância  unilateral
	0,1%	0,2%	0,5%	1%	2%	2,5%	5%
1	318,309	159,153	63,657	31,821	15,895	12,706	6,314
2	22,327	15,764	9,925	6,965	4,849	4,303	2,920
3	10,215	8,053	5,841	4,541	3,482	3,182	2,353
4	7,173	5,951	4,604	3,747	2,999	2,776	2,132
5	5,893	5,030	4,032	3,365	2,757	2,571	2,015
6	5,208	4,524	3,707	3,143	2,612	2,447	1,943
7	4,785	4,207	3,499	2,998	2,517	2,365	1,895
8	4,501	3,991	3,355	2,896	2,449	2,306	1,860
9	4,297	3,835	3,250	2,821	2,398	2,262	1,833
10	4,144	3,716	3,169	2,764	2,359	2,228	1,812
11	4,025	3,624	3,106	2,718	2,328	2,201	1,796
12	3,930	3,550	3,055	2,681	2,303	2,179	1,782
13	3,852	3,489	3,012	2,650	2,282	2,160	1,771
14	3,787	3,438	2,977	2,624	2,264	2,145	1,761
15	3,733	3,395	2,947	2,602	2,249	2,131	1,753
16	3,686	3,358	2,921	2,583	2,235	2,120	1,746
17	3,646	3,326	2,898	2,567	2,224	2,110	1,740
18	3,610	3,298	2,878	2,552	2,214	2,101	1,734
19	3,579	3,273	2,861	2,539	2,205	2,093	1,729
20	3,552	3,251	2,845	2,528	2,197	2,086	1,725
21	3,527	3,231	2,831	2,518	2,189	2,080	1,721
22	3,505	3,214	2,819	2,508	2,183	2,074	1,717
23	3,485	3,198	2,807	2,500	2,177	2,069	1,714
24	3,467	3,183	2,797	2,492	2,172	2,064	1,711
25	3,450	3,170	2,787	2,485	2,167	2,060	1,708
26	3,435	3,158	2,779	2,479	2,162	2,056	1,706
27	3,421	3,147	2,771	2,473	2,158	2,052	1,703

Tabela 4 | Distribuição t de Student (unilateral). Fonte: elaborada pela autora.

 

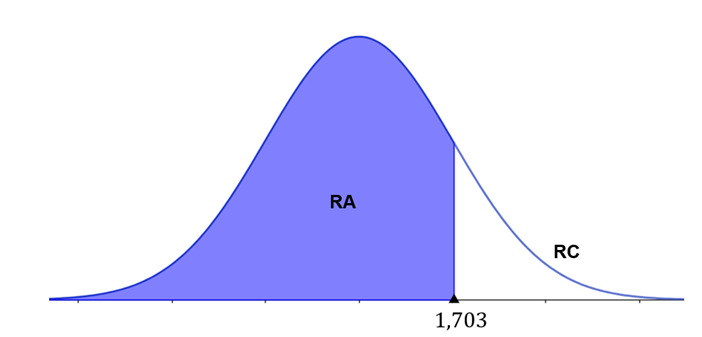
Com base nesse valor, nossa região de aceitação compreende todos os valores menores que 1,703, conforme ilustra a Figura 4.

• 5º Passo: calcular a estatística do teste

A estatística do teste t, com graus de liberdade, é denotada por:

$t_{calc}=t=\frac{\stackrel{-}{x}-\mu }{\sqrt{\frac{S^2}{n}}}$

$t_{calc}=\frac{\mathrm{52,04}-50}{\frac{\sqrt{25}}{\sqrt{28}}}\approx \mathrm{2,16}$

• 6º Passo: tomar a decisão

Temos que $t_{calc}>t_{tab}$, ou seja, $t_{calc}$ encontra-se na região crítica, logo rejeitamos $H_0$. Portanto, podemos concluir que a evidência amostral indica, ao nível de 5% de significância, que a média populacional é maior que 50 centímetros, confirmando assim a suspeita dos funcionários.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre os testes de hipóteses, sugerimos a leitura da seção 7.3 do livro Estatística aplicada. Após concluir a leitura da seção, escolha alguns exercícios para resolver! 

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023.

WERKEMA, C. Inferência estatística: como estabelecer conclusões com confiança no giro do PDCA e DMAIC. Rio de Janeiro: Grupo GEN, 2014. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788595152328/. Acesso em: 10 nov. 2023.

Regressão linear

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Realizamos inúmeras pesquisas e investigações com o objetivo de examinar as relações entre diversas variáveis. Um exemplo evidente é a conexão entre oferta e demanda. A motivação central para o estudo da interação entre duas variáveis está na habilidade de prever resultados futuros ou inferir valores não amostrados de uma população.

A regressão linear, uma técnica estatística, desempenha um papel crucial nesse contexto, permitindo a modelagem da relação entre duas variáveis. Essa capacidade é de suma importância em diversas áreas, incluindo economia, ciências sociais e engenharia.

Nesta aula, direcionaremos nossos esforços para compreender as características fundamentais da regressão linear. A fim de entender como podemos aplicar esse conceito, imagine que você é um gerente de uma loja de eletrônicos e está interessado em prever as vendas mensais com base em fatores específicos. Para simplificar, suponha que você tenha dados históricos de vendas mensais (em unidades) e o gasto mensal em publicidade (em reais) para os últimos 6 meses, conforme ilustra a Tabela 1.

Gasto com publicidade (multiplicar por R$ 1.000,00)	10	11	12,2	13,8	14,4	15,5
Unidades vendidas (multiplicar por 10000)	9,8	9,7	12,6	14,4	13,6	16,2

Tabela 1 | Dados referentes à venda e ao gasto com publicidade. Fonte: elaborada pela autora.

 

É possível prever as vendas mensais futuras com base no gasto com publicidade? Se você gastar R$ 18.000,00 em publicidade, qual será a previsão de vendas?

Para responder a essas perguntas, é necessário saber reconhecer a correlação entre duas variáveis e compreender como podemos conectá-las por meio de uma função.

Bons estudos!

Vamos Começar!

Até agora, dedicamos considerável atenção ao tratamento individual de cada variável, analisando-as em uma população específica. Essas análises, caracterizadas por esse enfoque, são chamadas de univariadas. No entanto, nem sempre nosso interesse reside na análise de uma única variável de cada vez, mas sim em estudar duas ou mais variáveis e compreender a relação entre elas. Essas análises são denominadas multivariadas. Nessa disciplina, restringiremos nosso estudo ao caso bivariado, ou seja, à análise simultânea de duas variáveis.

Suponha que um técnico em segurança esteja interessado em analisar se o número de horas de treinamento está relacionado com o número de acidentes de uma empresa. Como ele pode determinar se existe uma relação entre essas variáveis? É preciso encontrar o coeficiente de correlação. Uma correlação refere-se à relação entre duas variáveis, na qual os dados podem ser expressos como pares ordenados (x, y). Aqui, x representa a variável independente, enquanto y é a variável dependente (Larson; Farber, 2015). Se essa relação puder ser expressa por meio de função linear, temos uma correlação linear.

Um recurso visual que podemos empregar para examinar a correlação entre duas variáveis é o gráfico de dispersão, ou diagramas de dispersão. Essa ferramenta revela a presença, ou ausência, de relações entre as variáveis de um processo, mostrando sua intensidade ao representar duas ou mais variáveis, uma em relação à outra. Recomenda-se seu uso sempre que for necessário visualizar como uma variável responde às mudanças em outra, permitindo identificar potenciais relações de causa e efeito entre elas. Para a construção de um gráfico de dispersão, você deve localizar todos os pares ordenados (x, y) no plano cartesiano; o eixo horizontal representa os valores da variável independente x e o eixo vertical, os valores da variável dependente y. Na Figura 1, utilizamos os diagramas de dispersão para ilustrar algumas possibilidades de correlação.

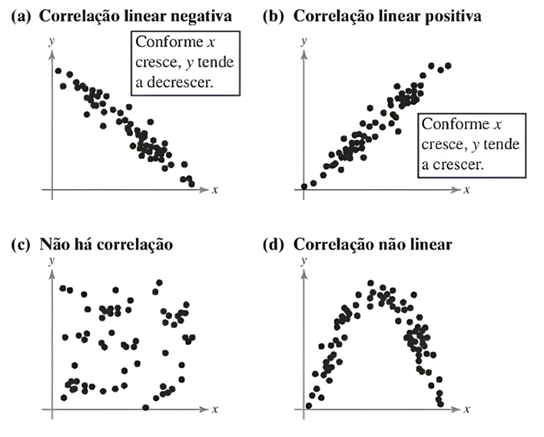
Analisar a correlação por meio de um gráfico de dispersão pode ser interpretativo. Uma abordagem apropriada para determinar a direção e medir a intensidade de uma correlação linear entre duas variáveis é calcular o coeficiente de correlação, também denominado coeficiente de correlação de Pearson. Para encontrarmos esse coeficiente, podemos utilizar a fórmula:

$r=\frac{n\cdot \sum xy-\left(\sum x\right)\left(\sum y\right)}{\sqrt{\left(n\cdot {\sum x}^2-{\left(\sum x\right)}^2\right)\left(n\cdot {\sum y}^2-{\left(\sum y\right)}^2\right)}}$

O valor do coeficiente de correlação varia entre -1 e 1, e temos que se:

$r=1$, a correlação é positiva perfeita.

$r>0$, a correlação é positiva.

$r<0$, a correlação é negativa

$r=0$, não há correlação entre as variáveis.

$r=-1$,  a correlação é negativa perfeita.

Podemos dizer que quanto mais próximo o valor de $\left|r\right|$ estiver de 1, mais forte é a correlação; à medida que o valor de $\left|r\right|$ se aproxima de 0, a correlação torna-se mais fraca.

Siga em Frente...

Uma sugestão para calcular o coeficiente de correlação é criar uma tabela que inclua todos os somatórios necessários, como exemplificado no caso a seguir.

 

Exemplo

Em uma competição de corrida, foram registrados dados sobre a idade e o peso dos participantes por meio de uma amostragem aleatória simples, resultando em uma amostra composta de 4 mulheres e 10 homens. Os dados das mulheres foram organizados na Tabela 2. Como podemos classificar a correlação entre a idade (x) e o peso (y) das mulheres?

Mulheres
Idade	Peso
18	60
20	62
23	65
27	58

Tabela 2 | Dados das mulheres. Fonte: elaborada pela autora.

 

Sabemos que o coeficiente de correlação é dado pela fórmula:

$r=\frac{n\cdot \sum xy-\left(\sum x\right)\left(\sum y\right)}{\sqrt{\left(n\cdot {\sum x}^2-{\left(\sum x\right)}^2\right)\left(n\cdot {\sum y}^2-{\left(\sum y\right)}^2\right)}}$

Para determinarmos esses somatórios, podemos construir uma tabela (Tabela 3).

$\mathit{x}$	$\mathit{y}$	${\mathit{x}}^2$	${\mathit{y}}^2$	$\mathit{x}\cdot \mathit{y}$
18	60	324	3600	1080
20	62	400	3844	1240
23	65	529	4225	1495
27	58	729	3364	1566
$\sum \mathit{x}=88$	$\sum \mathit{y}=245$	$\sum {\mathit{x}}^2=1982$	$\sum {\mathit{y}}^2=15033$	$\sum \mathit{x}\mathit{y}=5381$

Tabela 3 | Tabela de somatórios. Fonte: elaborada pela autora.$r=-\mathrm{0,26}$

 

Agora, substituímos esses somatórios na expressão:

$r=\frac{4\cdot 5381-88\cdot 245}{\sqrt{\left(4\cdot 1982-{\left(88\right)}^2\right)\left(4\cdot 15033-{\left(245\right)}^2\right)}}=-\frac{36}{\sqrt{19688}}\approx -\mathrm{0,26}$

Esse resultado nos mostra que há uma correlação negativa, porém muito fraca, visto que se aproxima de zero.

É fundamental ressaltar que correlação não sugere automaticamente uma relação de causa e efeito. Mesmo quando duas variáveis exibem uma correlação forte, isso não implica necessariamente uma ligação causal entre elas. Por outro lado, se as duas variáveis estão ligadas por uma relação de causa e efeito, elas estarão, por necessidade, correlacionadas. Lembre-se de que o principal propósito da análise da correlação linear é mensurar a intensidade de uma relação linear entre duas variáveis.

O termo coeficiente de determinação refere-se ao quadrado do coeficiente de correlação. Esse coeficiente expressa a proporção da variação da variável independente que é explicada pela variável dependente, servindo como uma métrica para avaliar a qualidade do ajuste. Além disso, ele pode ser entendido como a relação entre a variação explicada e a variação total:

$r^2=\frac{\mathrm{variação}\mathrm{ }\mathrm{explicada}}{\mathrm{variação}\mathrm{ }\mathrm{total}}$

No exemplo 1, encontramos $r=-\mathrm{0,26}$, sendo o coeficiente de determinação $r^2={\left(-\mathrm{0,26}\right)}^2=\mathrm{0,0676}$, isto é, 6,76%. Isso significa que apenas 6,76% da variação de y podem ser explicadas pela relação entre x e y.

Para expressarmos a variação da variável dependente com base nas variáveis independentes, podemos utilizar a regressão linear. O propósito da regressão linear é conduzir uma análise estatística para examinar a relação funcional entre uma variável dependente e uma ou mais variáveis independentes. Utilizando o método da regressão linear, construímos uma reta que melhor modela os dados; a equação dessa reta nos auxilia a encontrar possíveis valores de y dado um valor de x.

Compreendemos que a equação de uma reta é da forma $y=ax+b$, e precisamos determinar os valores dos coeficientes $a$ e $b$. Para isso, podemos empregar o método dos mínimos quadrados, que visa minimizar o erro quadrático médio, representado por S. Nosso foco aqui não é deduzir o método, mas sim simplesmente aplicar seu resultado. Ao utilizar o método dos mínimos quadrados para ajustar um conjunto de dados a uma reta específica, o coeficiente angular  será dado por:

$a=\frac{n\cdot \sum xy-\left(\sum x\right)\left(\sum y\right)}{n\cdot {\sum x}^2-{\left(\sum x\right)}^2}$

E o coeficiente linear $b$ será dado por:

$b=\frac{\left({\sum x}^2\right)(\sum y)-\left(\sum xy\right)\left(\sum x\right)}{n\cdot {\sum x}^2-{\left(\sum x\right)}^2}$

Ou: 

$b=\frac{\sum y}{n}-a\cdot \frac{\sum x}{n}$

A obtenção da reta de regressão é viável para qualquer conjunto de dados bivariados, independentemente da presença ou da ausência de correlação linear. O critério fundamental a ser considerado é o propósito de calcular a equação da reta: antecipar um valor de y para um dado valor de x. Nesse contexto, é sensato calcular a equação da reta de regressão apenas para conjuntos de dados bivariados que exibem uma correlação linear significativa, pois, em caso contrário, a realização de previsões concretas torna-se inviável.

Vamos Exercitar?

Agora, que você está familiarizado com todos os passos necessários para avaliar a correlação entre duas variáveis e calcular a reta de regressão, vamos voltar à nossa situação inicial, na qual você está interessado em verificar se há uma correlação entre o gasto com publicidade e as vendas mensais. Além disso, você deseja realizar algumas previsões com base nos dados coletados (Tabela 4).

Gasto com publicidade (multiplicar por R$ 1.000,00)	10	11	12,2	13,8	14,4	15,5
Unidades vendidas (multiplicar por 10000)	9,8	9,7	12,6	14,4	13,6	16,2

Tabela 4 | Dados referentes à venda e ao gasto com publicidade. Fonte: elaborada pela autora.

 

Para avaliarmos a existência de uma relação entre as variáveis e realizar previsões, é necessário calcular o coeficiente de correlação e determinar a reta de regressão para os dados. Em ambas as situações, é crucial obter informações específicas sobre os dados, começando pela identificação da variável dependente e da variável independente. Nota-se que, no contexto em que desejamos analisar se as vendas estão relacionadas ao gasto com publicidade, consideramos o gasto com publicidade como a variável x e as unidades vendidas, como a variável y. A Tabela 5 mostra as demais informações necessárias.

$\mathit{x}$	$\mathit{y}$	${\mathit{x}}^2$	${\mathit{y}}^2$	$\mathit{x}\cdot \mathit{y}$
10	9,8	100	96,04	98
11	9,7	121	94,09	106,7
12,2	12,6	148,84	158,76	153,72
13,8	14,4	190,44	207,36	198,72
14,4	13,6	207,36	184,96	195,84
15,5	16,2	240,25	262,44	251,1
$\sum \mathit{x}=\mathrm{76,9}$	$\sum \mathit{y}=\mathrm{76,3}$	$\sum {\mathit{x}}^2=\mathrm{1007,89}$	$\sum {\mathit{y}}^2=\mathrm{1003,59}$	$\sum \mathit{x}\mathit{y}=\mathrm{1004,08}$

Tabela 5 | Tabela de somatórios. Fonte: elaborada pela autora.

 

O coeficiente de correlação é dado por:

$r=\frac{n\cdot \sum xy-\left(\sum x\right)\left(\sum y\right)}{\sqrt{\left(n\cdot {\sum x}^2-{\left(\sum x\right)}^2\right)\left(n\cdot {\sum y}^2-{\left(\sum y\right)}^2\right)}}$

$r=\frac{6\cdot \mathrm{1004,08}-\mathrm{76,9}\cdot \mathrm{76,3}}{\sqrt{\left(6\cdot \mathrm{1007,89}-{\left(\mathrm{76,9}\right)}^2\right)\left(6\cdot \mathrm{1003,59}-{\left(\mathrm{76,3}\right)}^2\right)}}=\frac{\mathrm{157,01}}{\sqrt{\mathrm{26725,9405}}}=\mathrm{0,96}$

Logo, podemos concluir que as variáveis x (gastos com propaganda) e y (unidades vendidas) estão correlacionadas linear e positivamente. Podemos ainda calcular o coeficiente de determinação, obtido pelo quadrado do coeficiente de correlação, ou seja, $r^2={\left(\mathrm{0,96}\right)}^2=\mathrm{0,92}$.

Isso significa que 92% da variação de y podem ser explicadas pela relação entre x e y.

Agora vamos determinar qual é a reta de regressão. Sabemos que o coeficiente angular da reta é dado por:

$a=\frac{n\cdot \sum xy-\left(\sum x\right)\left(\sum y\right)}{n\cdot {\sum x}^2-{\left(\sum x\right)}^2}$

$a=\frac{6\cdot \mathrm{1004,08}-\mathrm{76,9}\cdot \mathrm{76,3}}{6\cdot \mathrm{1007,89}-{\left(\mathrm{76,9}\right)}^2}=\frac{\mathrm{157,01}}{\mathrm{133,73}}\approx \mathrm{1,17}$

E o coeficiente linear da reta é:

$b=\frac{\left({\sum x}^2\right)(\sum y)-\left(\sum xy\right)\left(\sum x\right)}{n\cdot {\sum x}^2-{\left(\sum x\right)}^2}$

$b=\frac{\mathrm{1007,89}\cdot \mathrm{76,3}-\mathrm{1004,08}\cdot \mathrm{76,9}}{6\cdot \mathrm{1007,89}-{\left(\mathrm{76,9}\right)}^2}=\frac{-\mathrm{311,745}}{\mathrm{133,73}}\approx -\mathrm{2,33}$

Assim, a reta de regressão correspondente é $y=\mathrm{1,17}x-\mathrm{2,33}$. Com base na equação da reta de regressão, podemos antecipar o número de unidades que serão vendidas com investimento de R$ 18.000,00 em publicidade. Para realizar essa previsão, substituímos o valor 18 no lugar da variável x. Utilizamos 18 em vez de 18.000,00, pois, em nossos cálculos, realizamos uma simplificação em relação às variáveis x e y, multiplicando os valores de x por 1000 e os valores de y por 10000. Assim, teremos:

$y=\mathrm{1,17}x-\mathrm{2,33}$

$y=\mathrm{1,17}\cdot 18-\mathrm{2,33}$

$y=\mathrm{21,06}-\mathrm{2,33}=\mathrm{18,73}$

Lembre-se de que esse valor deve ser multiplicado por 10000. Então, se forem gastos R$ 18.000,00 em publicidade, há uma previsão de que sejam vendidas 187.300 unidades. 

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre a regressão linear, sugerimos a leitura da seção 9.2 do livro Estatística aplicada. Após concluir a leitura da seção, escolha alguns exercícios para resolver!

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023.

WERKEMA, C. Inferência estatística: como estabelecer conclusões com confiança no giro do PDCA e DMAIC. Rio de Janeiro: Grupo GEN, 2014. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788595152328/. Acesso em: 10 nov. 2023.

Estatística inferencial

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Chegada

Olá, estudante!

Para desenvolver a competência desta unidade, que é compreender a importância e os princípios da inferência estatística, bem como distinguir os diferentes tipos de testes de hipóteses, você precisa primeiramente ser capaz de reconhecer as características relacionadas aos conceitos da estatística inferencial.

A estatística inferencial desempenha um papel crucial na análise e na interpretação de dados em diversas áreas, incluindo ciência, negócios, medicina, economia, entre outras. A estatística inferencial:

• Permite fazer inferências sobre uma população com base em uma amostra representativa dessa população.
• Fornece métodos para avaliar a probabilidade de certos eventos ocorrerem e ajuda na tomada de decisões mais informadas.
• É usada para testar hipóteses sobre parâmetros populacionais.
• É usada para prever tendências econômicas, avaliar o desempenho de investimentos e calcular riscos.

Um conceito fundamental para abordar problemas é o teorema do limite central, que fornece as informações necessárias para realizar inferências estatísticas sobre a média de determinada população. De acordo com esse teorema, quando amostras aleatórias de tamanho $n$, onde $n\ge 30$, são retiradas de uma população com média $\mu$ e desvio-padrão $\sigma$, a distribuição da média amostral se aproxima de uma distribuição normal. Isso implica no cálculo da probabilidade para uma distribuição amostral, visto que a distribuição da média amostral $\stackrel{-}{x}$ de uma amostra aleatória $n$ extraída de uma população não normal, com média $\mu$ e desvio-padrão $\sigma$, é aproximadamente normal, com média $\mu$ e desvio-padrão $\frac{\sigma }{\sqrt{n}}$.

Na estatística inferencial, a estimação de parâmetros emerge como uma técnica fundamental, empregando estatísticas amostrais para calcular o valor de um parâmetro populacional desconhecido. Essas estimativas podem adotar a forma de estimadores intervalares, delineando um intervalo de valores utilizado para estimar o mencionado parâmetro. A ideia é estabelecer um intervalo que, com um nível de confiança conhecido (denominado $1-\alpha$), abarque o valor real do parâmetro. O parâmetro $\alpha$ reflete o nível de significância, indicando a probabilidade de incorrer em erro ao afirmar que o parâmetro em questão está contido naquele intervalo. A depender das características da população, podemos ter diferentes formas de determinar um intervalo de confiança. No caso de uma população com média populacional $\mu$ e variância populacional ${\sigma }^2$, o intervalo de confiança será dado por:

$IC=\stackrel{-}{x}-z_{1-\alpha }\cdot \frac{\sigma }{\sqrt{n}}<\mu <\stackrel{-}{x}+z_{1-\alpha }\cdot \frac{\sigma }{\sqrt{n}}$

Outro princípio essencial na estatística inferencial é o teste de hipótese, um procedimento estatístico utilizado para tomar decisões ou realizar inferências sobre uma população com base em uma amostra de dados. No teste de hipótese, duas hipóteses opostas são definidas: a hipótese nula (H₀) e a hipótese alternativa (H₁). O resultado do teste auxilia a determinar se existem evidências estatísticas suficientes para rejeitar a hipótese nula em favor da hipótese alternativa. A hipótese nula deve expressar uma igualdade, enquanto a hipótese alternativa, complementar à nula, deve conter uma desigualdade estrita.

O teste de hipótese é construído com base no parâmetro da população em análise. Um dos testes tem como parâmetro a média populacional. Se a população tem média e variância populacional conhecidas, aplica-se o teste z para a média. Por outro lado, se a variância populacional não é conhecida, utiliza-se o teste t para a média.

Em situações que envolvem a previsão de dados populacionais com base em conjuntos de dados bivariados, a regressão linear emerge como uma ferramenta valiosa da estatística inferencial. Essa técnica possibilita modelar a relação entre duas variáveis, oferecendo insights significativos sobre a natureza da interdependência entre esses fenômenos. Para aplicarmos a regressão linear de maneira eficaz e derivar conclusões confiáveis, é necessário seguir alguns passos fundamentais.

Primeiramente, devemos identificar as variáveis de interesse e coletar um conjunto representativo de dados bivariados que envolvam essas variáveis. Em seguida, procedemos à análise estatística para determinar a reta de regressão. Além disso, é vital avaliar a qualidade do ajuste do modelo por meio de medidas como o coeficiente de determinação (r²). Essas avaliações proporcionam uma visão mais abrangente sobre a eficácia do modelo na representação da variabilidade nos dados.

Em síntese, é crucial adquirir um sólido entendimento de todos os princípios da estatística inferencial, dado que esses fundamentos desempenham um papel vital na abordagem e na solução de problemas nas mais diversas áreas. Ao dominar os princípios da estatística inferencial, você estará capacitado a realizar inferências valiosas e tomar decisões informadas com base em dados amostrais, contribuindo significativamente para a resolução eficaz de questões em contextos diversos. Esse conhecimento não apenas aprimora a capacidade de análise estatística, mas também amplia a aplicabilidade dessas habilidades em uma variedade de cenários, fortalecendo assim sua aptidão para enfrentar desafios analíticos em diferentes campos de estudo e prática profissional.

É Hora de Praticar!

Para contextualizar sua aprendizagem, imagine-se envolvido em um projeto de pesquisa universitária. Nesse projeto, a análise de dados coletados de uma amostra de estudantes é crucial para fazer inferências sobre toda a população estudantil. Os dados abrangem informações a respeito de desempenho acadêmico (média de notas) e tempo dedicado aos estudos, visando compreender a relação entre esses fatores e realizar previsões sobre o desempenho acadêmico global dos alunos.

Estudos anteriores revelaram que o desempenho acadêmico segue uma distribuição normal, com média populacional de 80 e desvio-padrão de 10. Em relação ao tempo dedicado aos estudos, pesquisas prévias indicam que, em média, os estudantes dedicam cerca de 5 horas por dia a essa atividade.

Com o propósito de avaliar se houve um aumento na média das notas, conduziu-se uma pesquisa com uma amostra de 60 alunos, resultando em uma média de notas de 78. Além disso, será realizado um teste de hipótese com um nível de significância de 5% para determinar se existem evidências estatísticas indicativas de um aumento nessa média.

Paralelamente, decidiu-se investigar se há diferenças na quantidade de horas estudadas por dia. Para isso, coletou-se uma amostra de 16 estudantes, obtendo uma média de estudo de 4,5 horas por dia, com um desvio-padrão amostral de 2 horas/dia. Um teste de hipótese com um nível de significância de 2% será realizado para verificar se há evidências estatísticas indicativas de mudança nessa média.

Reflita

Considerando a ampla variedade de situações em que os conceitos abordados na unidade podem ser aplicados, convidamos à reflexão sobre estas duas questões:

1. Como a estatística inferencial pode ser aplicada para tomar decisões estratégicas em um ambiente de negócios, utilizando dados amostrais para fazer inferências sobre a população?
2. Em que medida a estatística inferencial é utilizada em pesquisas científicas para generalizar resultados obtidos com base em uma amostra para uma população mais ampla, garantindo a validade e a confiabilidade dos estudos?

Resolução do estudo de caso

Primeiramente temos que realizar um teste de hipótese para verificar se houve um aumento na média de notas dos alunos. Temos as seguintes informações:

• Desempenho acadêmico segue uma distribuição normal.
• $\mu =80$.
• $\sigma =10$.
• Amostra com 60 alunos.
• $\stackrel{-}{x}=78$.
• $\alpha =5\%$.

Observe que como temos uma distribuição normal, $n>30$, e o desvio-padrão populacional, podemos aplicar um teste z para a média. Aplicaremos o teste para verificar se houve um aumento na média das notas.

1º Passo: formular as hipóteses

$H_0:\mu =80$

$H_1:\mu >80$

2º Passo: nível de significância de um teste

O nível de significância foi informado como $\alpha =5\%$.

3º Passo: definição da região crítica

Nossa hipótese alternativa é do tipo “maior que”, logo temos um teste unilateral à direita. A região crítica se encontra à direita da distribuição; então, para determinar o z-escore referente a essa área crítica, fazemos $1-\alpha$e encontramos a área à esquerda do z-escore. Precisamos identificar o valor de z cuja área à esquerda é $1-\mathrm{0,05}=\mathrm{0,95}$, e esse valor é $z_{\alpha }=\mathrm{1,64}$. A Figura 1 mostra a região crítica e a região de aceitação.

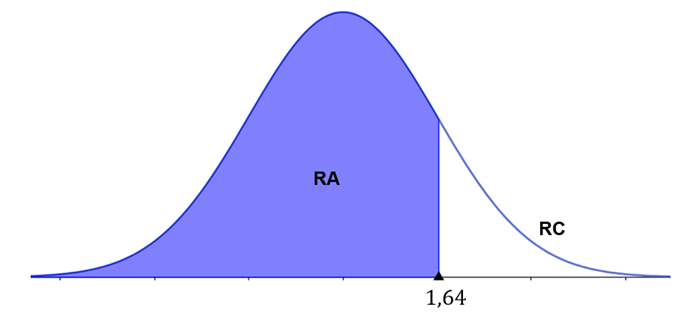
4º Passo: calcular a estatística com base na amostra

Como o objetivo é testar a média populacional da variável $X~ N (\mu ,{\sigma }^2)$, pelo teorema do limite central sabemos que a média amostral tem comportamento aproximadamente normal da forma $\stackrel{-}{x}~N\left(80,\frac{{10}^2}{60}\right)$, ou seja, $\stackrel{-}{x}~N\left(80;\mathrm{1,67}\right)$. $Z_{calc}$ (ou Z calculado) será dado por:

$z=\frac{\stackrel{-}{x}-\mu }{\frac{\sigma }{\sqrt{n}}}$

$z=\frac{78-80}{\frac{10}{\sqrt{60}}}=-\mathrm{1,55}$

5º Passo: tomar a decisão

Temos que $Z_{calc}<Z_{tab}$, ou seja, $Z_{calc}$ encontra-se na região de aceitação, logo podemos aceitar a hipótese nula. Isso significa que não há evidências estatísticas para afirmar que houve aumento na média das notas.

Agora temos que realizar um teste de hipótese para verificar se houve mudança na quantidade de horas estudadas por dia. Temos as seguintes informações:

• $\mu =5$.
• Amostra de 16 estudantes.
• $\stackrel{-}{x}=\mathrm{4,5}$.
• $S=2$.
• $\alpha =2$.

Perceba que temos uma amostra pequena, com $n<30$, e o desvio-padrão populacional é desconhecido, portanto precisamos aplicar um teste t para a média. 

1º Passo: formular as hipóteses

$H_0:\mu =5$

$H_1:\mu \ne 5$

2º Passo: nível de significância de um teste

O nível de significância foi informado como $\alpha =2\%$.

3º Passo: definição dos graus de liberdade $\left(\mathit{v}\right)$

Grau de liberdade  $v=n-1\to v=16-1=15$

4º Passo: definição da região crítica

Nossa hipótese alternativa é do tipo “diferente”, então temos um teste bilateral. Para determinarmos os limites da região de aceitação, precisamos dividir o nível de significância por dois. Assim, na tabela devemos buscar a interseção entre a coluna correspondente ao nível de significância de 1% e a linha dos graus de liberdade $v=15$. Assim, temos que $t_{\frac{\alpha }{2},v}=\mathrm{2,602}$. A Figura 2 ilustra a região crítica.

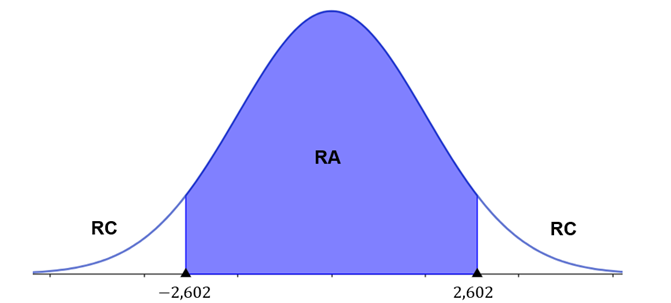
5º Passo: calcular a estatística do teste

A estatística do teste t, com $4$ graus de liberdade, é denotada por:

$t_{calc}=t=\frac{\stackrel{-}{x}-\mu }{\sqrt{\frac{S^2}{n}}}$

$t_{calc}=\frac{\mathrm{4,5}-5}{\frac{2}{\sqrt{16}}}\approx -1$

6º Passo: tomar a decisão

Temos que $t_{calc}>t_{tab}$, ou seja, $t_{calc}$ encontra-se na região de aceitação, logo aceitamos $H_0$.

Portanto, podemos concluir que não há evidência amostral que indique mudança na média de horas de estudo por dia.

Dê o play!

Assimile

Ao adentrar o domínio da estatística inferencial, é essencial ter uma compreensão abrangente dos diversos métodos disponíveis para enfrentar desafios, selecionando aquele mais apropriado de acordo com as particularidades específicas de cada situação. A Figura 3 resume os principais conceitos relacionados à estatística inferencial.

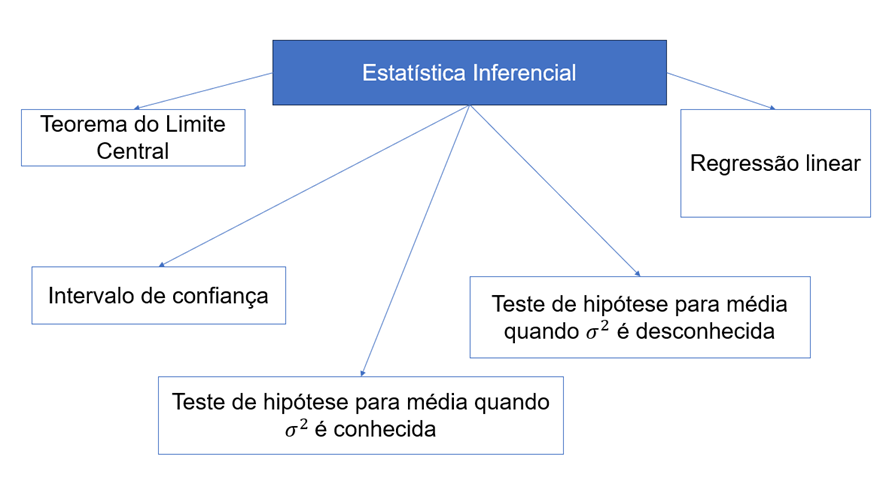
Referências

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023.

WERKEMA, C. Inferência estatística: como estabelecer conclusões com confiança no giro do PDCA e DMAIC. Rio de Janeiro: Grupo GEN, 2014. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788595152328/. Acesso em: 10 nov. 2023.