Cinemática - Movimento Uniforme e Uniformemente Variado

Aula 1

Grandezas Escalares e Grandezas Vetoriais

Grandezas escalares e grandezas vetoriais

Olá, estudante! Nesta videoaula, você conhecerá as grandezas escalares e as grandezas vetoriais. Grandezas escalares são aquelas que podem ser totalmente descritas apenas por um valor numérico e uma unidade. Grandezas vetoriais têm magnitude e direção. A maneira como se manipula matematicamente essas grandezas difere se elas são escalares ou se são vetoriais.

Esse conteúdo é importante para a sua prática profissional, pois você estará sempre lidando com dados, e esses podem ser escalares ou vetoriais.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Olá, estudante! Seja bem-vindo.

A física, como ciência experimental, fundamenta-se na realização de experimentos para compreender e descrever fenômenos naturais. Esses experimentos frequentemente envolvem a obtenção de medidas, as quais são quantificadas por meio de números. As grandezas utilizadas para descrever qualitativa ou quantitativamente um fenômeno observado são denominadas grandezas físicas, exemplos das quais incluem massa, altura, velocidade, tempo e distância.

Iniciaremos nossos estudos propondo um exemplo que trabalha com a grandeza física distância.

Em um campeonato de golfe, um jogador consegue acertar a bola no buraco realizando somente três tacadas: a primeira tacada desloca a bola $6 m$ para o norte; a segunda tacada desloca a bola $2 m$ para o leste; a terceira tacada desloca a bola para nordeste. Determine o módulo do deslocamento equivalente que poderia ser obtido com uma única tacada.

Bons estudos!

Vamos Começar!

Grandezas físicas

Grandezas físicas são propriedades mensuráveis que descrevem características dos objetos e fenômenos no universo. Elas podem ser classificadas em duas categorias principais: grandezas escalares e grandezas vetoriais.

Ao efetuarmos medidas de uma grandeza física, é costume compará-las a um padrão de referência, conhecido também como unidade. Esse padrão pode estar associado a um objeto específico ou a um procedimento experimental. É altamente desejável que os padrões escolhidos sejam naturais e permaneçam invariáveis ao longo do tempo.

O Sistema Internacional de Unidades (SI) é utilizado mundialmente por cientistas e engenheiros. Ele é composto por sete grandezas físicas fundamentais: metro (comprimento), quilograma (massa), segundo (tempo), kelvin (temperatura), mol (quantidade de matéria), candeia (intensidade luminosa) e Ampère (corrente elétrica). Muitas unidades derivadas do SI são definidas em termos das unidades fundamentais. Por exemplo, a unidade de força, Newton, é uma unidade derivada: $1 N = 1 k g . m / s^{2} .$

Muitas vezes, para expressar grandezas muito grandes ou muito pequenas, usamos notação científica e prefixos, que empregam potências de base $10$ .

$3456000000000 m = {3,456.10}^{12} m | 0,000000123 s = {1,23.10}^{- 7} s$

A Figura 1 apresenta os prefixos e símbolos das potências mais utilizadas.

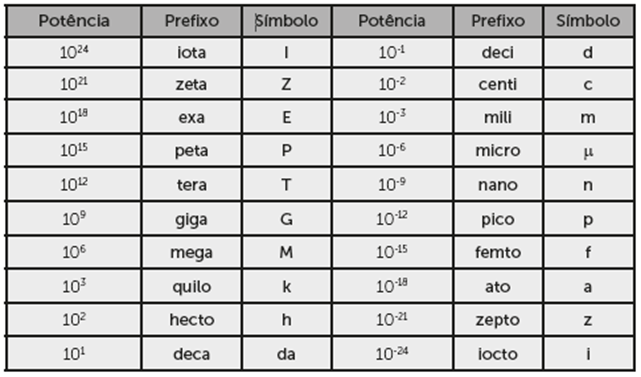
Figura 1 | Prefixos do SI. Fonte: adaptada de Inmetro (2012, p. 34).

Uma grandeza é escalar quando ela fica perfeitamente definida através de um número (módulo). Uma grandeza é vetorial quando, para seu perfeito entendimento, são necessários: módulo (valor numérico), direção e sentido (orientação). Tempo, massa e temperatura são exemplares de grandezas físicas cujas medidas e descrições são expressas exclusivamente por um valor numérico e uma unidade de medida.

Por outro lado, existem grandezas físicas que demandam informações adicionais para uma descrição completa e inequívoca, indo além do simples valor numérico. Tais grandezas, chamadas grandezas vetoriais, necessitam de dados relativos à orientação, como direção e sentido, para serem plenamente compreendidas. Exemplos incluem deslocamento, velocidade, aceleração e força. No caso das grandezas vetoriais, é comum utilizar uma representação simbólica, na qual uma letra é acompanhada por uma seta sobreposta ao seu símbolo. Exemplo: força ( $\vec{F}$ ).

Podemos representar geometricamente as grandezas vetoriais por meio de flechas, que chamamos de vetores. O módulo da grandeza deve ser indicado pelo comprimento total da flecha. A direção é indicada pelo segmento da reta e o sentido e indicado pela ponta da flecha.

Figura 2 | Vetor $\vec{V} = \vec{A B}$

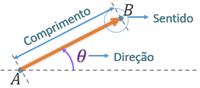
$|\vec{V}| = V$ é o módulo ou valor numérico que quantifica a grandeza; $θ$ (ângulo) é a direção que indica a linha sobre a qual o vetor está orientado (horizontal, vertical, norte-sul, leste-oeste, entre outras); $\pm$ significa o sentido, expressa a orientação do vetor sobre sua direção (direita ou esquerda, para cima ou para baixo, entre outros). Sobre o sentido, como não tem fundamento falar em um comprimento (módulo) negativo para o vetor, um sinal de menos na frente do vetor significa que o sentido foi invertido. Entenda: se $\vec{A}$ é um vetor com módulo, direção e sentido bem definidos, $\vec{B} = - 1 \vec{A} = - \vec{A}$ é um vetor de mesmo módulo, mesma direção e sentido oposto ao de $\vec{A}$ .

Na física, as direções horizontal e vertical são representadas pelo plano cartesiano $x y$ . O eixo $x$ representa a direção horizontal, e o $y$ , a vertical.

Temos vetores, chamados versores, que estão ligados aos eixos cartesianos. São chamados de versores pois seus módulos são iguais a 1. Eles guardam informações da sua direção e do seu sentido.

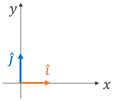
A direção horizontal (eixo $x$ ) tem sentido positivo para a direita (leste) e é representado pelo versor $\hat{i}$ , sendo que $|\hat{i}| = 1$ . Já a direção vertical (eixo $y$ ) tem sentido positivo para cima (norte) e é representado pelo versor $\hat{j}$ , sendo que $|\hat{j}| = 1$ . Qualquer vetor bidimensional pode ser escrito em termos desses versores. Exemplo: $\vec{v} = 2 \hat{i} - \hat{j}$ .

Uma característica importante de um vetor é o seu módulo, chamado também de norma ou tamanho.

Considere o vetor bidimensional $\vec{v} = v_{x} \hat{i} + v_{y} \hat{j}$ . O seu módulo é dado por:

$\vec{v} = v_{x} \hat{i} + v_{y} \hat{j}$

Antes de entrarmos em operações com vetores, analisaremos a decomposição de vetores. Considere a Figura 4.

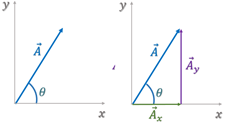
Denominamos:

${\vec{A}}_{x} = |{\vec{A}}_{x}| \hat{i}$ a componente, ou projeção horizontal de $\vec{A}$ no eixo $x$ .
${\vec{A}}_{y} = |{\vec{A}}_{y}| \hat{j}$ a componente, ou projeção vertical de $\vec{A}$ no eixo $y .$
$\vec{A} = {\vec{A}}_{x} + {\vec{A}}_{y}$ ou $\vec{A} = |{\vec{A}}_{x}| \hat{i} + |{\vec{A}}_{y}| \hat{j} .$

Analisando a figura, chegamos às seguintes relações:

$s e n θ = \frac{A_{y}}{A} \to |A_{y}| = A s e n θ$

$c o s θ = \frac{A_{x}}{A} \to |A_{x}| = A c o s θ$

Pelo Teorema de Pitágoras, temos que o módulo do vetor $\vec{A}$ é ${|\vec{A}|}^{2} = {|{\vec{A}}_{x}|}^{2} + {|{\vec{A}}_{y}|}^{2}$

Exemplo: considere os quatro vetores da Figura 5. (a) Como poderíamos representar esses vetores utilizando versores? (b) Calcule a projeção horizontal, a vertical e o módulo para o vetor $\vec{A}$ . (c) Encontre o ângulo de inclinação do vetor $\vec{A}$ com relação à horizontal.

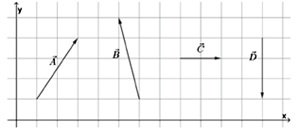
Figura 5 | Decomposição vetorial. Fonte: Oliveira (2016, p.).

(a) Podemos representar os vetores por meio de versores:

$\vec{A} = 2 \hat{i} + 3 \hat{j}$ $\vec{B} = - \hat{i} + 4 \hat{j}$ $\vec{C} = 2 \hat{i}$ $\vec{D} = - 3 \hat{j}$

(b) As componentes horizontal e vertical do vetor $\vec{A}$ são dadas por ${\vec{A}}_{x} = 2 \hat{i}$ e ${\vec{A}}_{y} = 3 \hat{j},$ e seu módulo é $A = \sqrt{2^{2} + 3^{2}} = 3,61 m$ .

(c) Desejamos $θ$ com relação à vertical, portanto $t g (θ) = A_{y} / A_{x} = 3 / 2$ . Utilizando a função inversa da tangente, obtemos o ângulo direção do vetor $A$ : $θ = a r c t g (3 / 2) \approx 56 °$ .

Siga em Frente...

Operações com vetores

Considere os vetores $\vec{A} = A_{x} \hat{i} + A_{y} \hat{j}$ , $\vec{B} = B_{x} \hat{i} + B_{y} \hat{j}$ e $\vec{C} = C_{x} \hat{i} + C_{y} \hat{j}$ . Podemos definir as seguintes operações:

Igualdade de vetores: para que $\vec{A} = \vec{B}$ , $A_{x} = B_{x}$ e $A_{y} = B_{y}$ .
Soma de vetores: $\vec{C} = \vec{A} + \vec{B} = A_{x} \hat{i} + A_{y} \hat{j} + B_{x} \hat{i} + B_{y} \hat{j} = (A_{x} + B_{x}) \hat{i} + {(A}_{y} + B_{y}) .$

A soma possui a propriedade comutativa, ou seja, a ordem da soma é irrelevante: $\vec{C} = \vec{A} + \vec{B} = \vec{B} + \vec{A}$ ; e a propriedade associativa, ou seja, é possível agrupar os vetores em qualquer ordem para somá-los: $\vec{A} + \vec{B}) + \vec{C} = \vec{A} + (\vec{B} + \vec{C}) .$

3. Multiplicação por um escalar $k$ : $\vec{C} = k \vec{A} = k A_{x} \hat{i} + k A_{y} \hat{j}$ A multiplicação por escalar não muda a orientação do vetor, mas o sentido mudará se $k < 0$ .

Exemplo: considere os vetores da Figura 5: $\vec{A} = 2 \hat{i} + 3 \hat{j}$ ; $\vec{B} = - \hat{i} + 4 \hat{j}$ ; $\vec{C} = 2 \hat{i}$ e $\vec{D} = - 3 \hat{j}$

Determine: $\vec{E} = \vec{A} + \vec{B} - \vec{C} + \vec{D}$ e $| \vec{E} |$

Resolução: $\vec{E} = (2 \hat{i} + 3 \hat{j}) + (- \hat{i} + 4 \hat{j}) - (2 \hat{i}) + (- 3 \hat{j})$

$\vec{E} = (2 - 1 - 2) \hat{i} + (3 + 4 - 3) \hat{j} = - \hat{i} + 4 \hat{j}$

$|\vec{E}| = \sqrt{{(- 1)}^{2} + 4^{2} \hat{j}} = \sqrt{17}$

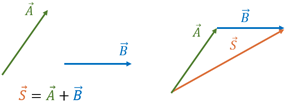
4. Regra do paralelogramo: é uma forma visual para entender a soma de vetores. O vetor resultante $\vec{S}$ é a diagonal do paralelogramo e é obtido conectando a extremidade inicial do primeiro vetor à extremidade final do segundo vetor (ou vice-versa). Tenha cuidado ao utilizar essa regra, pois a ordem dos vetores importa.

Exemplo:

Figura 6 | Regra do polígono para dois vetores

Vamos Exercitar?

Retornaremos ao exemplo proposto no início dessa seção.

Em um campeonato de golfe, um jogador consegue acertar a bola no buraco realizando somente três tacadas (veja a Figura 7a). Determine o módulo do deslocamento equivalente que poderia ser obtido com uma única tacada.

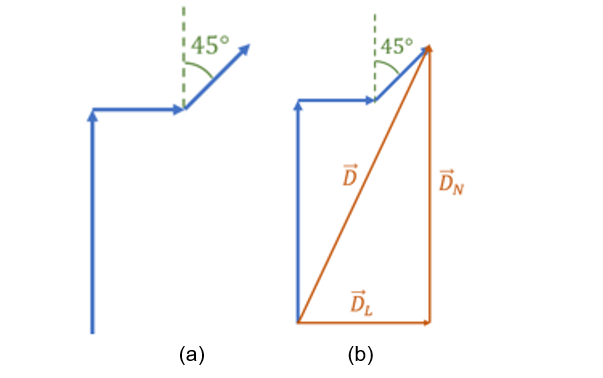
A primeira tacada desloca a bola $6 m$ para o norte; a segunda desloca a bola $2 m$ para o leste; a terceira tacada desloca a bola $2 m$ para nordeste.

O vetor da última tacada deve ser decomposto em componente para o norte e componente para o leste.

Tendo como base a Figura 7b, podemos representar o vetor deslocamento total $\vec{D}$ em função dos vetores deslocamentos para o leste ( ${\vec{D}}_{L}$ ) e para o norte ( $\vec{D}_N$ ).

Logo, o deslocamento total na direção norte: $D_{N} = (6) + (2) c o s 45 \to D_{N} = 7,4 m$ .

O deslocamento total na direção leste: $D_{L} = (2) + (2) s e n 45 \to D_{L} = 3,4 m$ .

Então, o deslocamento total será: $D = \sqrt{D_{N}^{2} + D_{L}^{2}} \to D = \sqrt{{(7,4)}^{2} + {(3,4)}^{2}} \to D ≅ 8 m$

Saiba Mais

Para que você tenha um melhor conhecimento sobre o Sistema Internacional de Unidades e as grandezas fundamentais. Para saber mais sobre padrões de comprimento, massa e tempo, análise dimensional, conversão de unidades e estimativas e cálculos de ordem de grandeza e algarismos significativos, leia o Capítulo 1 da obra indicada a seguir:

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

Veja mais operações com vetores (produto e componentes de vetores) e familiarize-se com o conceito e o uso de versores (vetores unitários). Leia o Capítulo 3 do livro:

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

Você já conhece as simulações interativas da Universidade de Colorado? As sims PhET baseiam-se em extensa pesquisa em educação e envolvem os alunos através de um ambiente intuitivo, estilo jogo, em que os alunos aprendem através da exploração e da descoberta. Acesse, em especial, o simulador Adição de Vetores.

Referências Bibliográficas

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

INSTITUTO NACIONAL DE METROLOGIA, NORMALIZAÇÃO E QUALIDADE INDUSTRIAL. Sistema internacional de unidades. 8. ed. Duque de Caxias: Inmetro/CICMA/SEPIN, 2012 Disponível em: http://www.inmetro.gov.br/inovacao/publicacoes/si_versao_final.pdf. Acesso em: 19 dez. 2023.

OLIVEIRA, P. B. Física geral e experimental: mecânica. Londrina: Editora e Distribuidora Educacional S.A., 2016.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

Aula 2

Posição, Deslocamento, Velocidade e Aceleração Médias e Instantâneas

Posição, deslocamento, velocidade e aceleração médias e instantâneas

Olá, estudante! Nesta videoaula, você conhecerá as principais grandezas da cinemática: trajetória, posição, espaço, deslocamento, velocidade média e velocidade instantânea e aceleração média e aceleração instantânea. A cinemática estuda o movimento dos corpos sem considerar as causas dele. Esse conteúdo é importante para a sua prática profissional, pois essas grandezas são relevantes na análise de movimento, seja o movimento uniforme ou uniformemente variado.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Olá, estudante! Seja bem-vindo.

Um dos objetivos da Física é estudar o movimento dos objetos: a rapidez com que se movem, ou a distância que percorrem no espaço em um determinado tempo. Você sabe, por exemplo, quantos metros um carro percorre até parar quando você pisa no freio? Quando um objeto escorrega da sua mão, quanto tempo você tem para segurá-lo antes que ele atinja o solo? Nesta seção, estudaremos as equações de movimento, velocidade e aceleração média e instantânea, e você aprenderá a responder a essas perguntas.

Para nos ajudar a entender as grandezas da cinemática, propomos este exemplo: em uma jornada interestadual, partindo de São Lourenço (MG) com destino a Campos do Jordão (SP), um ônibus percorreu $60 k m$ em $80 m i n$ . Após $10 m i n$ de parada, seguiu viagem por mais $90 k m$ à velocidade média de $60 k m / h$ . Por fim, após $13 m i n$ de parada, percorreu mais $45 k m$ em $30 m i n$ .

A afirmativa verdadeira sobre o movimento do ônibus, do início ao final da viagem, é que ele:

Percorreu uma distância total de $160 k m$ .
Gastou um tempo total igual ao triplo do tempo gasto no primeiro trecho de viagem.
Desenvolveu uma velocidade média de $60,2 k m / h$ .
Não modificou sua velocidade média em consequência das paradas.
Desenvolveu uma velocidade média de $58,6 k m / h$ , se não tivesse feito paradas.

Bons estudos!

Vamos Começar!

Posição de um ponto material

Quando nos dedicamos ao estudo do movimento de um objeto, a consideração de suas dimensões torna-se um ponto crucial. O conceito de ponto material, conhecido também como partícula, refere-se a um corpo cujas dimensões são tão pequenas que podem ser desprezadas em comparação com as distâncias envolvidas no movimento analisado. Em contraste, quando as dimensões do objeto desempenham um papel significativo, denominamos esse objeto como um corpo extenso, ou ainda, um corpo rígido.

Para ilustrar essa distinção, tomemos o exemplo de um carro em deslocamento. Se estivermos analisando uma viagem extensa, digamos de São Paulo à Bahia, as dimensões do carro podem ser consideradas desprezíveis em comparação com a vastidão da trajetória percorrida. Nesse caso, o carro pode ser tratado como um ponto material.

Trajetória e espaço

Trajetória de um ponto material é a união de todas as posições por onde o ponto material passou em um determinado tempo. Imagine um avião deixando um rastro de fumaça em um espetáculo aéreo. Sua trajetória fica marcada por ele.

Quando a trajetória do objeto é uma reta, dizemos que o movimento e retilíneo. Toda trajetória deve ter um sentido de orientação. Uma consideração importante é que a trajetória depende do referencial adotado, que pode ser entendido como o observador em relação ao qual pretendemos estudar um movimento qualquer.

Por exemplo, imagine que você está dentro de um carro em movimento e lança uma bola para cima. Para você, a bola apenas faz uma trajetória em linha reta de subida e descida. Agora, imagine a mesma situação, porém observada por uma pessoa parada na calçada. Para essa pessoa, a bola faz uma trajetória curvilínea (como uma parábola), pois, além de subir e descer, há também o movimento na horizontal do carro. Assim, a trajetória da bola é diferente em cada caso, pois depende do referencial adotado.

Denominamos espaço (representado pela letra $s$ ) a localização do objeto na sua trajetória com base em um ponto denominado de origem dos espaços ( $s_{0}$ ). Assim, o espaço ( $s$ ) é um indicador de local (posição), isto é, responde à pergunta “onde está o objeto?”. O espaço ( $s$ ) não indica a distância percorrida e pode ser um valor positivo, negativo ou nulo.

Podemos avaliar a variação de posição de um objeto através do seu deslocamento $∆ s$ . Vale ressaltar que o deslocamento é uma grandeza vetorial. Assim, é necessário adotar sentido positivo para o deslocamento, e quando o móvel se deslocar no sentido oposto, seu deslocamento será negativo. Veja a Figura 1:

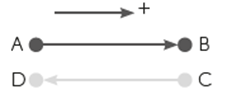
Figura 1 | Deslocamento: grandeza vetorial. Fonte: Oliveira (2016, p.)

Se adotarmos o sentido positivo para a direita, o deslocamento de A para B é positivo, enquanto o deslocamento de C para D é negativo. O deslocamento é dado por:

$∆ s = s_{f i n a l} - s_{i n i c i a l}$

A letra grega maiúscula $∆$ – delta – é usada para representar a variação de uma grandeza e corresponde à diferença entre o valor final e o valor inicial.

Siga em Frente...

Equação horária do movimento

Quando um ponto material está em movimento, sua posição ( $s$ ) varia no decorrer do tempo ( $t$ ). Assim, podemos dizer que $s = f (t)$ , e que essa é a função horária do movimento. É importante indicar as unidades das variáveis $s$ e $t$ na equação. No SI, metros e segundos, respectivamente.

Exemplo: a seguir, temos duas equações do movimento de objetos que podem ser aproximados por pontos materiais. Encontre a posição das partículas nos instantes $0 s$ . $1,0 s$ e $5,0 s$ .

(a) $s = 8,0 + 3,0 . t (S I)$

(b) $s = 3,0 {. t}^{2} (S I)$

$t$	$s = 8,0 + 3,0 . t$	$s = 3,0 {. t}^{2}$
$t = 0 s$	$s = 8,0 + 3,0.0 = 8,0 m$	$s = 3,0.0 = 0 m$
$t = 1 s$	$s = 8,0 + 3,0.1 = 8,0 + 3,0 = 11,0 m$	$s = 3,0 {. t}^{2} = {3,0.1}^{2} = 3,0 m$
$t = 5 s$	$s = 8,0 + 3,0.1 = 8,0 + 3,0 = 11,0 m$	$s = 3,0 {. t}^{2} = {3,0.5}^{2} = 75,0 m$

Tabela 1 | Posições das partículas

Velocidade

Se quisermos medir a taxa de variação da posição com o tempo, temos o conceito de velocidade. Quanto mais rápida a mudança de posição no tempo, maior a velocidade do objeto.

A velocidade é uma grandeza vetorial. Quando queremos saber apenas o módulo (o valor) da velocidade de um objeto, estudamos a velocidade escalar dele. Quando a velocidade é positiva, isso significa que o objeto se move no sentido positivo da trajetória (movimento progressivo). Quando a velocidade for negativa, significa que o objeto se move no sentido negativo da trajetória (movimento retrogrado). Se a posição de um objeto não varia no tempo, dizemos que ele está em repouso (sua velocidade é nula).

Velocidade média

Considere um carro viajando de São Paulo para o Rio de Janeiro (400 km). Durante a viagem, o painel do carro mostra velocidades diferentes. Às vezes, o carro está mais rápido (velocidade maior); em outros momentos, está mais devagar (velocidade menor). Podemos calcular uma média da velocidade do carro durante o trajeto percorrido. Chamaremos essa grandeza de velocidade média. Se o carro percorreu os 400 km em 5 horas, podemos dizer que, em média, o carro percorreu 80 km a cada hora. Assim, podemos definir que a velocidade média ( $v_{m}$ ) é dada por:

$v_{m} = \frac{s_{f} - s_{i}}{t_{f} - t_{i}} \to v_{m} = \frac{∆ s}{∆ t}$

Em que: $s_{f}$ = espaço (posição) final no tempo final considerado ( $t_{f}$ ); $s_{i}$ = espaço (posição) inicial no tempo inicial considerado ( $t_{i}$ ); $∆ s$ (delta $s$ ) = variação dos espaços (deslocamento); $∆ t$ (delta $t$ ) = variação do tempo.

No SI, a velocidade média $v_{m}$ é medida em metros por segundo (m/s).

Velocidade instantânea

Voltemos ao exemplo do carro que viaja de São Paulo para o Rio de Janeiro. A velocidade média que acabamos de definir é uma medida fictícia, como se no painel do carro, durante toda a viagem, estivesse marcando sempre 80 km/h, o que de fato não ocorre. A velocidade variável mostrada no painel do carro a cada instante da viagem é a chamada velocidade instantânea. Na linguagem da Física, dizemos que a velocidade em um dado instante é aproximada a partir da velocidade média com o intervalo de tempo $∆ t$ muito pequeno. Quanto mais próximo de zero o intervalo de tempo $∆ t$ tomado, mais nos aproximaremos de um valor limite, que é a velocidade instantânea $v$ .

Em cálculo, você estuda o processo conhecido como limite, portanto você poderá tomar o limite da velocidade média com $∆ t \to 0$ , obtendo a velocidade instantânea. Estudará, também, como fazer derivadas e saberá obter a velocidade instantânea, calculando a derivada da posição com relação ao tempo.

Exemplo: uma partícula parte do repouso e começa a se movimentar. A posição dela é dada pela equação $s = 12 t^{2} - 2 t^{3}$ (SI). Determine: (a) a posição inicial $s_{0}$ da partícula; (b) a posição da partícula quando $t = 4,0 s$ ; (c) a velocidade média da partícula entre $t = 0 s$ e $t = 4,0 s$ .

Resolução:

(a) Substituindo $t = 0 s$ na equação, temos $s_{0}$ : $s = 12 {. 0}^{2} - 2 {. 0}^{3} = 0 m$ .

(b) Substituindo $t = 4,0 s$ na equação, temos $s_{0}$ : $s = 12 {. 4,0}^{2} - 2 {. 4,0}^{3} = 64,0 m .$

$v_{m} = \frac{64 - 0}{4 - 0} = 16 m / s .$

Aceleração

Quando a velocidade de um objeto em movimento varia com o tempo, dizemos que o objeto possui aceleração. A aceleração também é uma grandeza vetorial, e ela descreve a taxa de variação da velocidade com o tempo. A aceleração também pode ser positiva ou negativa. Quando o produto entre a velocidade e a aceleração for positivo, isso significa que a aceleração é a favor do movimento e que o movimento é acelerado. Quando o produto entre a velocidade e a aceleração for negativo, isso significa que a aceleração é contrária ao movimento e que o movimento é retardado.

Se um objeto possui aceleração nula, significa que a velocidade dele não varia no tempo, ou seja, a velocidade é constante.

Aceleração média

A aceleração média $a_{m}$ é dada por:

$a_{m} = \frac{v_{f} - v_{i}}{t_{f} - t_{i}} \to a_{m} = \frac{∆ v}{∆ t}$

Em que: $v_{f}$ = velocidade final no tempo final considerado ( $t_{f}$ ); $v_{i}$ = velocidade inicial no tempo inicial considerado ( $t_{i}$ ); $∆ v$ (delta $v$ ) = variação da velocidade; $∆ t$ (delta $t$ ) = variação do tempo.

No SI, a aceleração média $a_{m}$ é medida em metros por segundo ao quadrado ( $m / s^{2}$ ).

Aceleração instantânea

A aceleração instantânea mede a taxa de variação da velocidade em um dado instante, ou seja, se o intervalo de tempo considerado tender a zero, a aceleração média tende a um valor que é denominado de aceleração instantânea. Portanto, podemos dizer que a aceleração instantânea é o limite da aceleração média, quando o intervalo de tempo considerado tende a zero.

Sinal da velocidade ( $v$ )	Sinal da aceleração ( $a$ )	Sinal de $v \times a$	Módulo da velocidade	Classificação
+	+	+	aumenta	progressivo acelerado
+	-	-	diminui	progressivo retardado
-	+	-	diminui	retrógrado e retardado
-	-	+	aumenta	retrógrado e acelerado

Tabela 2 | Classificação do movimento em relação à velocidade e à aceleração

Vamos Exercitar?

Retornaremos ao exemplo proposto no início dessa seção: em uma jornada interestadual, partindo de São Lourenço (MG) com destino a Campos do Jordão (SP), um ônibus percorreu diferentes trechos a velocidades variadas. Detalharemos cada etapa da viagem na Tabela 3. Trabalharemos com deslocamento em km, tempo em horas e velocidade em km/h.

Trecho	Deslocamento	Tempo	Velocidade
1	60 km	80/60 = 1,33 h	60/1,33 = 45,11 km/h
2	0	10/60 = 0,17 h	0
3	90 km	90/60 = 1,50 h	60 km/h
4	0	0,22 h	0
5	45 km	0,50 h	45/0,5 = 90 km/h
Soma	195 km	3,72 h

Tabela 3 | Dados da viagem

(a)O ônibus percorreu $∆ s = 195 k m$ na viagem, portanto a alternativa (a) está incorreta.

(b) No primeiro trecho da viagem, o ônibus gastou $1,33 h$ , e o tempo total da viagem foi $∆ t = 3,72 h \neq 3 (1,33) h$ , portanto a alternativa (b) está incorreta.

$v_{m} = \frac{195}{3,72} = 52,40 k m / h$

(d)A alternativa está incorreta, pois o tempo de parada diminui sua velocidade média.

(e)A alternativa está correta. Se o ônibus não tivesse parado, teríamos: $∆ t = 3,72 - 0,17 - 0,22 = 3,33 h,$ e sua velocidade média seria:

$v_{m} = \frac{195}{3,33} = 58,56 k m / h$

Saiba Mais

Você sabia que o cálculo fornece ferramentas para obter as velocidades e acelerações instantâneas? São os limites e as derivadas, que você conhecerá em seu curso de cálculo. Veja mais no Capítulo 2 do livro:

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

Você conhece o site da Khan Academy, com cursos, aulas e prática on-line gratuitos? Nele você encontra vários vídeos e artigos sobre os temas explorados nessa seção.

Aproveite!

Referências Bibliográficas

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física, volume 1: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

OLIVEIRA, P. B. Física geral e experimental: mecânica. Londrina: Editora e Distribuidora Educacional S.A., 2016.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

Aula 3

Movimento Uniforme e Variado e Queda Livre

Movimento uniforme e queda livre

Olá, estudante! Nesta videoaula, você conhecerá o movimento uniforme, o movimento uniformemente variado e o movimento em queda livre. Esse conteúdo é importante para a sua prática profissional, pois, embora o movimento uniforme seja um caso simplificado, seu estudo é necessário, pois ele é frequentemente usado na descrição de situações do mundo real e fornece uma base para compreender conceitos mais avançados.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Olá, estudante! Seja bem-vindo.

O estudo do movimento dos corpos é uma área fundamental da Física conhecida como mecânica. A mecânica clássica, desenvolvida por cientistas, como Isaac Newton, fornece um quadro teórico para entender como os corpos se movem. Existem duas partes principais na mecânica clássica: a cinemática e a dinâmica. A cinemática lida com a descrição do movimento, incluindo conceitos como posição, velocidade, aceleração e trajetória. A dinâmica, por outro lado, trata das causas do movimento, como forças e suas relações com a massa e a aceleração.

Vamos nos aprofundar na análise dos movimentos, explorando as variações da posição, da velocidade e da aceleração? Analisar tais grandezas pode revelar informações valiosas e nos permitir reconstruir o movimento de um objeto de maneira detalhada.

Para ilustrar os novos conceitos, resolveremos a seguinte situação: um automóvel trafega com velocidade constante de 12 m/s por uma avenida e se aproxima de um cruzamento onde há um semáforo com fiscalização eletrônica. Quando o automóvel se encontra a uma distância de 30 m do cruzamento, o sinal muda de verde para amarelo. O motorista deve decidir entre parar o carro antes de chegar ao cruzamento ou acelerar o carro e passar pelo cruzamento antes do sinal mudar para vermelho. Esse sinal permanece amarelo por 2,2 s. O tempo de reação do motorista (tempo decorrido entre o momento em que o motorista vê a mudança de sinal e o momento em que realiza alguma ação) é 0,5 s. (a) Determine a mínima aceleração, suposta constante, que o carro deve ter para parar antes de atingir o cruzamento e não ser multado. (b) Calcule a menor aceleração constante que o carro deve ter para passar pelo cruzamento sem ser multado.

Bons estudos!

Vamos Começar!

Movimento uniforme e variado e queda livre de corpos

Nesta seção, estudaremos os três tipos distintos de movimentos: o movimento uniforme, caracterizado por uma constante e invariável velocidade; o movimento uniformemente variado, no qual a aceleração é constante, resultando em variação uniforme da velocidade; a queda livre, um fenômeno que ocorre quando um objeto é deixado livremente em direção à Terra. Cada um desses movimentos apresenta características únicas e, ao compreendê-los, ampliaremos nossa compreensão do fascinante mundo da cinemática.

Movimento uniforme (MU)

Para prever como será o comportamento da posição como função do tempo, é necessário conhecer as equações de movimento do corpo, chamadas também de equações horárias.

Em relação a um dado referencial (sistema de coordenadas), um movimento é chamado de uniforme quando o objeto percorre distâncias iguais para intervalos de tempos iguais, ou seja, quando a velocidade é constante e, portanto, não há aceleração. Assim, podemos generalizar dizendo que o movimento é uniforme (MU) quando a função horária dos espaços é de primeiro grau, ou seja:

$s = s_{0} + v t$

Na cinemática, o parâmetro $s_{0}$ representa o espaço (posição) inicial do objeto e o parâmetro $v$ representa a velocidade média. No MU, $v$ é sempre constante e diferente de zero, portanto a aceleração é nula.

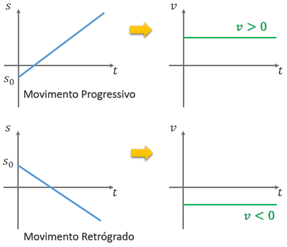
Figura 1 | Gráficos do movimento uniforme (MU)

Movimento uniformemente variado (MUV)

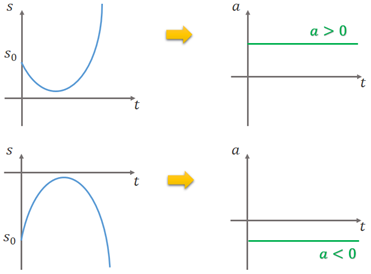
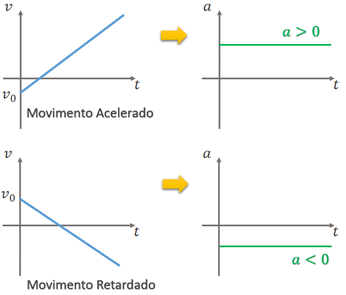
O movimento uniformemente variado (MUV) caracteriza-se pela variação da velocidade no decorrer do tempo devido à presença de uma aceleração constante e diferente de zero. O movimento é uniformemente variado (MUV) quando a função horária dos espaços é de segundo grau, ou seja,

$s = s_{0} + v_{0} t + \frac{a t^{2}}{2}$

Na cinemática, o parâmetro $s_{0}$ representa a posição (espaço) inicial do objeto, o parâmetro $v_{0}$ representa a velocidade escalar inicial, e o parâmetro $a$ representa a aceleração, que é uma constante não nula e é dada por $a = ∆ v / ∆ t$ .

No MUV, a função horária dos espaços é $s = s_{0} + v_{0} t + a t^{2} / 2$ e, como a velocidade varia com o tempo devido à aceleração constante, temos a função horária da velocidade:

$v = v_{0} + a t$

Além disso, no MUV, podemos relacionar o deslocamento com a velocidade em uma equação independente do tempo, por meio da Equação de Torricelli:

$v^{2} = v_{0}^{2} + 2 a ∆ s$

Figura 2 | Gráficos do movimento uniforme (MUV)

Figura 3 | Gráficos do movimento uniforme (MUV)

Exemplo: um avião, ao decolar, percorre 1,20 km no solo com aceleração constante, partindo do repouso, em um intervalo de tempo de 20 s. (a) Calcule a aceleração (SI) do avião durante a decolagem. (b) Calcule a velocidade (em km/h) com que o avião se desprende do solo. (c) Confirme o deslocamento total do avião no processo de decolagem usando a Equação de Torricelli.

Resolução:

(a) Como há aceleração, concluímos que se trata de MUV. Nesse movimento, temos que $s = s_{0} + v_{0} t + a t^{2} / 2$ . Como o avião parte do repouso: $v_{0} = 0$ , então:

$∆ s = \frac{a t^{2}}{2} \to 2 ∆ s = a t^{2} \to a = \frac{2 ∆ s}{t^{2}}$

Substituindo os dados fornecidos:

$a = \frac{2 (1200)}{20^{2}} = 6,0 m / s^{2}$

(b) Temos que $v = v_{0} + a t$ , como $v_{0} = 0$ , $v = a t$ :

$v = (6,0) (20) = 120 m / s = 432 k m / h$

$v^{2} = 2 a ∆ s \to ∆ s = \frac{v^{2}}{2 a}$

$∆ s = \frac{120^{2}}{2 (6)} \to ∆ s = 1200 m = 1,2 k m$

O resultado está de acordo com o enunciado.

Siga em Frente...

Queda livre

Quando um objeto se movimenta sob ação exclusiva de um campo gravitacional (aceleração da gravidade) e quando podemos desprezar o efeito do ar, dizemos que ele está em queda livre. A queda livre é um caso especial do movimento uniformemente variado (MUV).

A aceleração da gravidade, representada pela letra $g$ , é uma grandeza física vetorial com direção vertical e sentido para baixo. O módulo da aceleração da gravidade varia de um local para outro. Mesmo no planeta Terra, o módulo da aceleração da gravidade varia dependendo da altitude do local. Adotaremos o módulo da aceleração da gravidade na Terra como $g = 9,8 m / s^{2}$ .

Considere um objeto abandonado do repouso ( $v_{0} = 0$ ) de uma altura $h$ acima do solo, em um local onde a aceleração da gravidade é $g$ e o efeito do ar é desprezível. Observe que esse objeto se deslocará apenas na direção vertical e para baixo. Nesse tipo de movimento, costumamos adotar o sentido para baixo como positivo.

Temos sempre a liberdade de escolher o sentido positivo de nossos eixos $x y$ , desde que sejamos coerentes com a definição do início ao fim do cálculo. A aceleração da gravidade $g$ possui sentido para baixo, portanto, entrará positiva nas equações da queda livre.

Devido à presença da aceleração constante da gravidade, esse movimento de queda livre e um MUV. Portanto:

$s = s_{0} + v_{0} t + \frac{g t^{2}}{2} \to ∆ s = \frac{g t^{2}}{2}$

Em que utilizamos $v_{0} = 0$ (parte do repouso).

Repare que, quando tiver transcorrido o tempo de queda $t_{q}$ , o objeto terá percorrido toda a altura $h$ , ou seja, quando $t = t_{q} \to ∆ s = h$ , portanto, substituindo na equação do deslocamento, concluímos:

$h = \frac{g}{2} t_{q}^{2} \to t_{q} = \sqrt{\frac{2 h}{g}}$

A velocidade do objeto em queda livre a qualquer instante é dada por $v = v_{0} + g t$ . A velocidade do objeto em relação à distância percorrida é dada pela Equação de Torricelli:

$v^{2} = v_{0}^{2} + 2 g ∆ s$

Partindo do repouso, quando o objeto chega ao solo em queda livre, podemos concluir a velocidade de chegada, que é dada por

$v_{f}^{2} = v_{0}^{2} + 2 g h \to v_{f} = \sqrt{2 g h}$

Exemplo: um vaso de flores cai, a partir do repouso, da janela de um prédio de uma altura $h = 45 m$ acima do solo. Despreze o efeito do ar e considere $g = 9,8 m / s^{2}$ . Calcule: (a) o tempo de queda ( $t_{q}$ ) do vaso até atingir o solo e (b) o módulo da velocidade do vaso ao atingir o solo.

Resolução:

(a) No movimento de queda livre, temos que $∆ s = v_{0} t + g t^{2} / 2$ . Como o vaso parte do repouso, temos que $v_{0} = 0$ , logo $∆ s = g t^{2} / 2$ . Repare que, quando tiver transcorrido o tempo de queda $t_{q}$ , o objeto terá percorrido toda a altura $h$ , ou seja, quando $t = t_{q} \to ∆ s = h$ . Assim, substituindo na equação anterior, temos:

$h = \frac{g t_{q}^{2}}{2} \to t_{q} = \sqrt{\frac{2 h}{g}} \to t_{q} = \sqrt{\frac{2 (45)}{9,8}} \to t_{q} \approx 3,0 s$

(b) Pela Equação de Torricelli, temos $v^{2} = v_{0}^{2} + 2 g ∆ s$ , sendo $v_{0} = 0$ . Logo:

$v^{2} = 2 g h \to v = \sqrt{2 g h} \to v = \sqrt{2 (9,8) (45)} \to v \approx 29,7 m / s$

Vamos Exercitar?

Retornaremos ao exemplo proposto no início dessa seção.

O tempo de reação do motorista é de $0,5 s$ . Durante esse tempo, ele percorre:

$∆ s = v t \to ∆ s = (12) (0,5) \to ∆ s = 6 m$

(a) Utilizaremos a Equação de Torricelli para encontrar a aceleração que o carro deve ter para parar antes de atingir o cruzamento e não ser multado.

$v^{2} = v_{0}^{2} + 2 a ∆ s$

$0^{2} = 12^{2} + 2 a (30 - 6)$

$0 = 144 + 48 a$

$a = \frac{- 144}{48} \to a = - 3 m / s^{2}$

(b) Para calcular a menor aceleração constante que o carro deve ter para passar pelo cruzamento sem ser multado, utilizaremos a equação horária do MUV:

$s = s_{0} + v_{0} t + \frac{1}{2} a t^{2}$

$24 = 0 + 12 (1,7) + \frac{1}{2} a {(1,7)}^{2}$

$1,445 a = 24 - 20,4$

$a = \frac{3,6}{1,445} \to a = 2,5 m / s^{2}$

O tempo utilizado pelo motorista será de $(2,2 - 0,5) = 1,7 s$ .

Saiba Mais

Você pode aprofundar seus conhecimentos nos movimentos estudados lendo o Capítulo 3 do livro:

HEWITT, P. G. Física conceitual. 13. ed. Porto Alegre: Bookman, 2023.

Você conhece o site da Khan Academy, com cursos, aulas e prática on-line gratuitos? Nele você encontra vários vídeos e artigos sobre os temas explorados nessa seção. Aproveite!

Referências Bibliográficas

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física, volume 1: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

HEWITT, P. G. Física conceitual. 13. ed. Porto Alegre: Bookman, 2023.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

Aula 4

Movimento Bidimensional

Olá, estudante! Nesta videoaula, você conhecerá dois movimentos que acontecem no plano. O lançamento de projétil é um problema clássico em Física e Engenharia, e as suas equações são úteis para analisar e prever o comportamento de um projétil em movimento. O movimento circular uniforme é encontrado em muitos contextos, como em objetos em órbita, pêndulos em pequenos ângulos, rodas giratórias, entre outros. As equações e os conceitos associados a esse tipo de movimento são fundamentais na Física e na Engenharia.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Olá, estudante! Seja bem-vindo.

O estudo dos movimentos dos corpos é desafiador e fundamental para compreendermos os fenômenos ao nosso redor. Que tal nos aprofundarmos um pouco mais na análise dos movimentos?

Exploraremos a cinemática de uma partícula movimentando-se em duas dimensões. Saber o básico sobre o movimento bidimensional permitirá o exame de uma variedade de situações, desde o movimento de satélites em órbita até o movimento de elétrons em um campo elétrico uniforme.

Trataremos o movimento de projéteis e o movimento circular uniforme como casos especiais do movimento em duas dimensões.

Para ilustrar os novos conceitos, resolveremos a seguinte situação: um navio que protege a entrada do porto de uma ilha localiza-se a 560 m dessa ilha. Um canhão de defesa, situado ao nível do mar, dispara balas com uma velocidade inicial igual a 82 m/s. (a) Com que ângulo, medido a partir da horizontal, se deve disparar uma bala para que ela acerte o navio? (b) A que distância o navio deveria estar do canhão para estar fora do alcance máximo das balas de canhão? Considere a aceleração da gravidade como 9,8m/s². Despreze a resistência do ar.

Bons estudos!

Vamos Começar!

Movimento bidimensional

O movimento bidimensional refere-se ao deslocamento de um objeto em um plano que possui duas dimensões espaciais, geralmente representadas como eixos perpendiculares. Esses eixos são frequentemente designados como eixo $x$ e eixo $y$ , formando um sistema de coordenadas que possibilita a descrição completa da posição de um objeto no plano.

Ao analisar o movimento bidimensional, a cinemática torna-se mais complexa do que em um movimento unidimensional, pois agora precisamos considerar tanto a variação na posição ao longo do eixo $x$ quanto ao longo do eixo $y$ .

Lançamento de projéteis

O lançamento de projéteis, ou movimento balístico, é um fenômeno clássico da mecânica que descreve o movimento de um objeto que é arremessado para o ar, seguindo uma trajetória parabólica sob a influência da gravidade. Esse tipo de movimento é comumente observado em situações, como o lançamento de uma bola, um foguete ou até mesmo uma pedra.

A análise matemática do lançamento de projéteis é frequentemente dividida em dois componentes: movimento horizontal e movimento vertical.

Consideremos um projétil lançado obliquamente, sob ação da gravidade terrestre ( $g = 9,8 m / s^{2}$ ), com velocidade inicial $v_{0}$ inclinada de um ângulo $θ$ em relação ao plano horizontal de lançamento. Adotaremos o ponto de lançamento como a origem dos espaços, $x_{0} = 0$ e $y_{0} = 0,$ e os sentidos para cima e para a direita como sentidos positivos, como mostra a Figura 1.

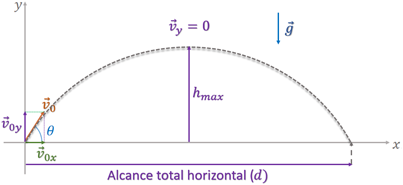
Figura 1 | Lançamento oblíquo de um projétil

Observe que, nessa situação, o objeto, lançado obliquamente, apresenta um arco de parábola como trajetória, ou seja, o objeto realiza um movimento vertical (de subida e descida) e um movimento horizontal. Assim, para analisar o movimento do projétil, precisaremos decompor o movimento em vertical e horizontal e analisá-los separadamente, de acordo com o princípio da independência dos movimentos de Galileu. As componentes horizontal e vertical do movimento de um projétil são completamente independentes uma da outra e podem ser tratadas separadamente, com o tempo sendo a variável comum para ambas as componentes (Serway; Jewett Jr., 2017).

As componentes horizontal e vertical da velocidade inicial $v_{0}$ são:

Figura 2 | Velocidade inicial do movimento

$|{\vec{v}}_{o x}| = |{\vec{v}}_{o}| c o s θ$

$|{\vec{v}}_{o y}| = |{\vec{v}}_{o}| s e n θ$

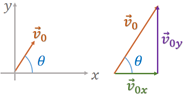
De acordo com Galileu, movimentos em direções diferentes, perpendiculares, são independentes e podem ser estudados separadamente. Assim, dividiremos o estudo do movimento do projétil em movimento vertical e horizontal. Para diferenciar, no movimento balístico, não usaremos a letra $s$ para indicar o deslocamento. Usaremos a letra $y$ para indicar o deslocamento vertical e a letra $x$ para indicar o deslocamento horizontal.

Na vertical, temos a presença da aceleração da gravidade ( $g$ ). A presença da aceleração caracteriza o movimento uniformemente variado (MUV). O movimento na vertical refere-se à subida e à descida do objeto. O deslocamento na vertical será representado pela letra $y$ . Precisamos adotar um sentido positivo para analisar o movimento vertical. Adotaremos o sentido para cima como positivo. Observe, portanto, que a aceleração da gravidade será negativa, pois seu sentido é para baixo.

O movimento no eixo vertical apresenta as seguintes características:

Função horária dos espaços:

$y = {y_{0} + v}_{0 y} t + \frac{a t^{2}}{2} \to y = v_{o} s e n θ t - \frac{g t^{2}}{2}$

Em que definimos o ponto de lançamento como a origem dos espaços $(y_{0} = 0)$ . $v_{0 y} = v_{0} s e n θ$ e $a = - g$ (pois adotamos o sentido para cima como positivo e, em relação a ele, a aceleração da gravidade é negativa, logo tem sentido para baixo).

Função horária da velocidade vertical:

$v_{y} = v_{0 y} + a t \to v_{y} = v_{o} s e n θ - g t$

Equação de Torricelli:

$v^{2} = v_{0}^{2} + 2 a ∆ s \to v_{y}^{2} = v_{0}^{2} {(s e n θ)}^{2} - 2 g ∆ y$

No eixo horizontal, não temos aceleração, portanto o movimento horizontal é uniforme (MU) e determina o alcance do objeto. O deslocamento horizontal será representado pela letra $x$ . Esse movimento apresenta as seguintes características:

Função horária dos espaços:

$x = x_{0} + v_{x} t \to x = v_{o} (c o s θ) t$

Em que $x_{0} = 0$ , pois o ponto de lançamento é a origem dos espaços e $v_{x} = v_{0 x} = v_{o} c o s θ$ , pois a componente horizontal da velocidade é sempre constante e diferente de zero no movimento balístico.

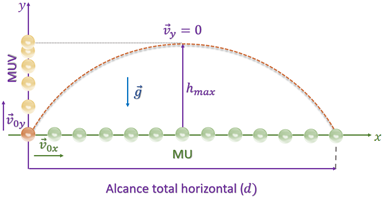
No lançamento de um projétil, é importante sabermos que, no ponto mais alto da trajetória, a componente vertical da velocidade é nula $v_{y} = 0$ . Lembre-se de que a componente horizontal da velocidade ( $v_{x}$ ) é sempre constante nesse movimento.

Utilizando as equações apresentadas anteriormente, é possível desenvolver as equações para calcular o tempo de subida $t_{s}$ (que é igual ao tempo de queda $t_{q}$ ), o tempo total da trajetória $t_{t o t a l}$ , a altura máxima $h_{m a x}$ e o alcance total horizontal $d$ .

O tempo total da trajetória é dado por:

$t_{t o t a l} = t_{s} + t_{q} \to t_{t o t a l} = \frac{2 v_{0} s e n θ}{g}$

A altura máxima $h_{m a x}$ e o alcance total horizontal $d$ são dados por:

$h_{m a x} = \frac{v_{0}^{2} {(s e n θ)}^{2}}{2 g} d = v_{0}^{2} s e n 2 θ$

Movimento circular uniforme

Movimento circular uniforme (MCU) é o movimento no qual um corpo se move em uma trajetória em formato de circunferência com velocidade de módulo constante. O movimento da hélice de um ventilador é um exemplo de um movimento em nosso dia a dia que pode ser considerado MCU.

Quando um corpo executa um MCU, sua velocidade é um vetor com valor constante, configurando-se sempre tangente à trajetória executada, variando, assim, a orientação.

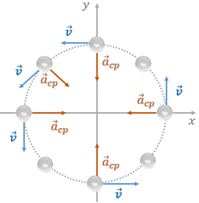
Aceleração é a grandeza física relacionada à variação da velocidade. No MCU, o valor da velocidade é constante, porém ela sofre variações em sua orientação. A aceleração relacionada com essas variações de orientações do vetor velocidade é denominada aceleração centrípeta ( ${\vec{a}}_{c p}$ ). O vetor aceleração centrípeta está sempre orientado para o centro da trajetória em formato de circunferência, sendo assim, por consequência, perpendicular ao vetor velocidade em cada instante, conforme a ilustração da Figura 2, que representa o MCU executado por um corpo.

Figura 4 | Representação dos vetores velocidade e aceleração centrípeta

Siga em Frente...

Sabendo o valor da velocidade do corpo que está executando o MCU e o raio ( $R$ ) de sua trajetória, a intensidade do vetor aceleração centrípeta é determinada por $a_{c p} = v^{2} / R$ .

Como o MCU é um movimento que se repete ao longo do tempo, podemos definir duas importantes grandezas: período e frequência. Período ( $T$ ) é o intervalo de tempo necessário para que o corpo em MCU execute uma volta completa. Sua unidade de medida no SI é o segundo. A frequência ( $f$ ) define a quantidade de voltas executadas por unidade de tempo. No SI, sua unidade de medida é repetições (ou rotações) por segundo e é chamada de hertz ( $H z$ ). O período é o inverso da frequência ( $T = 1 / f$ ).

A trajetória do MCU é uma circunferência, o que possibilita que esse movimento seja estudado utilizando-se características dessa forma geométrica, definindo, assim, algumas grandezas angulares.

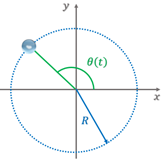
O ângulo de uma volta completa é $360 °$ ou $2 π r a d$ ( $r a d$ é a abreviatura da unidade de medida radiano). Se um ponto material executa um MCU, podemos definir para ele uma velocidade angular ( $ω$ ), que corresponde ao deslocamento angular ( $∆ θ$ ) pelo intervalo de tempo. Sua unidade de medida no SI é o $r a d / s$ :

$ω = \frac{∆ θ}{∆ t}$

Um ponto em MCU percorre o comprimento ( $C$ ) de uma circunferência a cada intervalo de tempo. Sendo $C = 2 π R$ para uma volta, podemos escrever a velocidade do ponto da seguinte forma:

$v = \frac{∆ s}{∆ t}$

Para uma volta completa:

$v = \frac{2 π R}{T} \to ω = 2 π f R$

Como $ω = 2 π / T = 2 π f$ , das relações dadas, concluímos que podemos obter a velocidade multiplicando a velocidade angular pelo raio: $v = ω R$ .

Exemplo: o ponteiro dos segundos de um relógio analógico de parede mede $12 c m$ e executa um MCU. Determine: (a) seu período e frequência; (b) sua velocidade angular; (c) a velocidade de um ponto na sua extremidade; (d) sua aceleração centrípeta.

Resolução:

(a) O ponteiro dos segundos de um relógio analógico executa uma volta completa a cada um minuto, ou 60 segundos, de forma que $T = 60 s$ . Sua frequência é dada por $f = 1 / T = 1 / 60 \approx 0,017 H z .$

(b) $ω = 2 π f \to ω = 2 π (0,017) \approx 0,105 r a d / s$ .

(d) $a_{c p} = v^{2} / R \to a_{c p} = {(0,013)}^{2} / (0,12) \approx 0,0014 m / s^{2}$ .

Vamos Exercitar?

Retornaremos ao exemplo proposto no início dessa seção: um navio que protege a entrada do porto de uma ilha localiza-se a 560 m dessa ilha. Um canhão de defesa, situado ao nível do mar, dispara balas com uma velocidade inicial igual a 82 m/s.

(a) Com que ângulo ( $θ$ ), medido a partir da horizontal, deve-se disparar uma bala para que ela acerte o navio?

O alcance ( $d$ ) da bala de canhão é dado por:

$d = \frac{v_{0}^{2}}{g} s e n 2 θ \to s e n 2 θ = \frac{d g}{v_{0}^{2}} \to s e n 2 θ = \frac{(560) (9,8)}{82^{2}} \to s e n 2 θ = 0,816$

Usando a função inversa do seno:

$2 θ = a r c s e n (0,816) \to θ = \frac{a r c s e n (0,816)}{2}$

O seno é positivo no primeiro e no segundo quadrantes, portanto:

$θ = \frac{1}{2} \{\begin{matrix} 54,7 ° (p r i m e i r o q u a d r a n t e) \\ 125,3 ° (s e g u n d o q u a d r a n t e) \end{matrix}$

Logo, tanto para $θ = 27 °$ como para $θ = 63 °,$ o navio será avariado.

(b) A que distância o navio deveria estar do canhão para estar fora do alcance máximo das balas de canhão?

O alcance será máximo se $θ = 45 °$ , logo:

$d = \frac{v_{0}^{2}}{g} s e n 2 θ \to d = \frac{82^{2}}{9,8} s e n (2.45) \to d = 686 m .$

Saiba Mais

Veja mais no Capítulo 4 do livro:

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

Você já conhece as simulações interativas da Universidade de Colorado? As sims PhET baseiam-se em extensa pesquisa em educação e envolvem os alunos através de um ambiente intuitivo, estilo jogo, em que eles aprendem através da exploração e da descoberta. Acesse, em especial, o simulador Movimento de Projétil.

Você conhece o site da Khan Academy, com cursos, aulas e prática on-line gratuitos? Nele você encontra vários vídeos e artigos sobre os temas explorados nessa seção.

Referências Bibliográficas

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física, volume 1: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

Encerramento da Unidade

Cinemática - Movimento Uniforme e Uniformemente Variado

Videoaula de Encerramento

Olá, estudante! Nesta videoaula, você verá uma síntese dos principais conceitos abordados na unidade. Esses conceitos são fundamentais para a compreensão do movimento em uma e duas dimensões. Esse conteúdo é importante para a sua prática profissional, pois o entendimento dele é essencial para a compreensão de muitos fenômenos naturais e tem aplicações em várias disciplinas científicas e tecnológicas.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Chegada

Olá, estudante!

Para desenvolver a competência desta unidade, que é compreender as grandezas fundamentais da cinemática e saber aplicar seus conceitos envolvendo práticas do cotidiano, você deverá, primeiramente, conhecer os conceitos fundamentais das grandezas da cinemática: posição, deslocamento, velocidade, aceleração, além dos movimentos uniforme e uniformemente variado, lançamento oblíquo e movimento circular uniforme. Eles são frequentemente aplicados para descrever o movimento de objetos em várias situações, proporcionando uma compreensão matemática e quantitativa do movimento.

É Hora de Praticar!

Você trabalha em uma operadora de monitoramento e rastreamento de trens e percebe a seguinte situação de perigo: um trem vermelho a 72 km/h e um trem azul a 144 km/h estão na mesma linha, retilínea e plana, movendo-se em direções opostas (um em direção ao outro). Quando a distância entre os trens é de 950 m, você percebe a gravidade da situação e avisa os dois maquinistas para acionarem imediatamente os freios, fazendo com que os dois trens sofram uma desaceleração de 1,0 m/s². Com essas informações, você precisa saber se os trens conseguem frear a tempo de evitar uma colisão para poder avisar seus superiores sobre uma possível situação de emergência.

Reflita

Testes rápidos

(1) A física envolve mais do que a resolução de problemas, mas isso é uma grande parte dela. Às vezes, enquanto você está se esforçando para fazer suas tarefas de casa, pode parecer que isso é tudo que você faz. Porém, a repetição e a prática são partes importantes da aprendizagem. Você precisa desenvolver a mesma filosofia em relação à solução de problemas de matemática e de física: é preciso praticar usando boas técnicas de resolução de problemas. Esse trabalho trará enormes dividendos, não apenas durante o restante deste curso de Física, não apenas nos exames, nem mesmo apenas nas outras aulas de ciência, mas por toda a sua carreira. O que constitui, passo a passo, uma boa estratégia de resolução de problemas?

(2) O estudo da Física é dividido em diversas partes, e uma delas é a cinemática, que é o estudo do movimento dos objetos. Esses objetos podem ser, por exemplo, carros, bolas de beisebol, planetas ou átomos. Inicialmente, desprezamos toda a estrutura interna de um objeto em movimento e o consideramos como um ponto material, ou objeto puntiforme, ou seja, para determinar as equações de movimento para um objeto, imaginamos que ele esteja localizado em um único ponto no espaço a cada instante de tempo. Que ponto de um objeto devemos escolher para representar sua localização?

(3) A resistência do ar refere-se à força que atua contra o movimento de um objeto à medida que ele se desloca através do ar. Essa força é influenciada pela velocidade do objeto, por sua forma e pela densidade do ar. A resistência do ar é um fator significativo em muitas áreas. Você saberia dizer algumas delas?

Resolução do estudo de caso

Analisaremos qual é o espaço que cada um dos trens precisa percorrer para poder parar completamente.

Para o trem vermelho: $v = 72 k m / h \to v = 20 m / s e a = - 1,0 m / s^{2}$

Para conseguir parar, a velocidade do trem deve zerar, assim, temos que:

$a = \frac{∆ v}{∆ t} = \frac{(v_{f} - v_{i})}{∆ t} \to ∆ t = \frac{(v_{f} - v_{i})}{a} \to ∆ t = \frac{0 - 20}{- 1} \to ∆ t = 20 s$

O trem vermelho vai levar 20 segundos para frear completamente. Nesse processo de frenagem, temos que o módulo da velocidade média é:

$v = \frac{(v_{i} - v_{f})}{2} \to v = \frac{20 - 0}{2} \to v = 10 m / s$

Assim, a distância percorrida durante a frenagem é:

$v = \frac{∆ s}{∆ t} \to ∆ s = v ∆ t \to ∆ s = 10.20 \to ∆ s = 200 m$

Portanto, o trem vermelho precisa percorrer 200 m até parar completamente.

Para o trem azul: $v = 144 k m / h \to v = 40 m / s e a = - 1,0 m / s^{2}$

Para conseguir parar, a velocidade do trem deve zerar, assim, temos que:

$a = \frac{∆ v}{∆ t} = \frac{(v_{f} - v_{i})}{∆ t} \to ∆ t = \frac{(v_{f} - v_{i})}{a} \to ∆ t = \frac{0 - 40}{- 1} \to ∆ t = 40 s$

O trem azul levará 40 segundos para frear completamente. Nesse processo de frenagem, temos que o módulo da velocidade média é:

$v = \frac{(v_{i} - v_{f})}{2} \to v = \frac{40 - 0}{2} \to v = 20 m / s$

Assim, a distância percorrida durante a frenagem é:

$v = \frac{∆ s}{∆ t} \to ∆ s = v ∆ t \to ∆ s = 20.40 \to ∆ s = 800 m$

Portanto, o trem azul precisa percorrer 800 m até parar completamente.

A distância total percorrida pelos dois trens até poderem parar completamente é de $∆ s_{t o t a l} = 200 + 800 = 1000 m$ .

Como a distância entre eles é de 950 m, haverá colisão e será necessário avisar os supervisores sobre a situação de emergência.

Dê o play!

Assimile

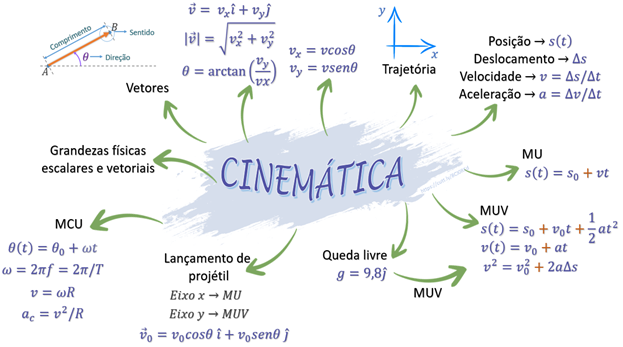Referências

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física, volume 1: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

HEWITT, P. G. Física conceitual. 13. ed. Porto Alegre: Bookman, 2023.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

TIPLER, P. A.; MOSCA, G. Física para cientistas e engenheiros: volume 1: mecânica, oscilações e ondas, termodinâmica. Rio de Janeiro: LTC, 2023.