Investimento

Valor futuro e aplicações

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você se aprofundará nos estudos relacionados a investimentos, desde sua definição, utilização e como podemos usar fórmulas matemáticas para calcular investimentos com depósitos periódicos e iguais. 
Para melhor compreender sobre o assunto, imagine que você fez uma aplicação para utilizar o dinheiro em uma viagem. Sendo assim, qual foi resultado de uma aplicação mensal de R$ 20.000,00, durante 3 anos sob regime de juros compostos e taxa de 1,20% a.m.?
Para isso, vamos dar início ao nosso estudo!

Vamos Começar!

Investimentos

Muitas pessoas acabam tendo dúvidas sobre o que é um investimento, que é considerando qualquer valor capaz de gerar um lucro, seja em um período de curto, médio ou longo prazo.
As pessoas optam por investir seu dinheiro para adquirir algo no futuro, seja uma viagem, compra um imóvel ou móvel, para ter rendimentos, rendas, entre outros. Um investimento é toda aplicação de dinheiro visando ganhos. Vejamos alguns exemplos de aplicação:

• Caderneta de poupança.
• Fundos.
• Ações.

Antes de escolher um investimento, faz-se necessário planejar e estudar os demais tipos de investimentos existentes no mercado. Para isso, alguns conceitos discutidos na Matemática Financeira podem contribuir bastante. 

Siga em Frente...

Cálculo do valor futuro

Ao trabalharmos com investimentos, podemos utilizar o cálculo do valor futuro, que está embasado no resultado de uma aplicação com depósitos iguais e periódicos. Para determinar o valor futuro, usamos a seguinte fórmula matemática:

$V\mathrm{F}=\mathrm{dep}.\left[\frac{{(1+i)}^n-1}{i}\right]$

Em que:

• VF: valor futuro; resultado da aplicação ou investimento.
• dep: refere-se ao valor do depósito.
• n: número total de depósitos periódicos e iguais.
• i: taxa de juros compostos. 

Um exemplo disso pode ser uma pessoa que queira aplicar um determinado valor sempre no mesmo dia, em uma aplicação que renda um valor x de taxa de juros compostos. Após um determinado período de depósitos, se obtém o valor final, ou seja, o valor futuro. 

Resultado de aplicações

Para encontrarmos o resultado de uma aplicação, ou seja, o valor futuro, ou valor de depósitos periódicos e iguais, ou período, fazemos uso da fórmula do valor futuro. Para melhor compreender, observe um exemplo:
Em uma determinada instituição financeira, uma aplicação que paga uma taxa de juros compostos de 1,2% a.m. após dois anos apresentou um valor futuro de R$ 8.839,27. Sendo assim, qual o valor dos depósitos mensais e iguais que foram realizados nesse período?
Primeiramente, vamos extrair os valores do problema:

$VF: R\$ 8.839,27$

$dep:?$

n: 24 depósitos periódicos e iguais.

Substituindo na fórmula:

$VF=dep\left[\frac{{\left(1+i\right)}^n-1}{i}\right]$

Temos, 

$8 \mathrm{839,27}=dep\left[\frac{{\left(1+\mathrm{0,012}\right)}^{24}-1}{\mathrm{0,012}}\right]$

$8 \mathrm{839,27}=dep\left[\frac{\mathrm{0,3315}}{\mathrm{0,012}}\right]$

$8 \mathrm{839,27}=dep·\mathrm{27,6250}$

$dep=\frac{8 \mathrm{839,27}}{\mathrm{27,6250}}=\mathrm{319,97}$

Logo, o valor de cada depósito foi de R$ 319,97.

Vamos Exercitar?

Para colocar em prática os conceitos vistos, imagine que você fez uma aplicação para realização de uma viagem. Sendo assim, qual foi resultado de uma aplicação mensal de R$ 20.000,00, durante 3 anos sob regime de juros compostos e taxa de 1,20% a.m.?
Primeiramente, vamos extrair os valores do problema:

• VF: Resultado final da aplicação.
• dep: R$ 20.000,00 por mês.
• n: 36 depósitos periódicos e iguais, pois trata-se de depósitos mensais durante três anos.

Substituindo os valores na fórmula, temos:

$VF=dep\left[\frac{{\left(1+i\right)}^n-1}{i}\right]$

Temos,

$i:\mathrm{1,20}\% a.m$

$VF=20.000\left[\frac{{\left(1+\mathrm{0,012}\right)}^{36}-1}{\mathrm{0,012}}\right]$

$VF=20.000\left[\frac{\mathrm{1,5364}-1}{\mathrm{0,012}}\right]$

$VF=20.000·\mathrm{44,70}$

$VF=R\$\mathrm{894.000,00}$

Logo, o resultado da aplicação final é de R$ 894.000,00.

Saiba Mais

Para saber mais sobre investimentos, leia o artigo Análise de investimentos de Luiz Henrique Figueira Marquezan.

Referências Bibliográficas

ASSAF NETO, A.. Matemática financeira e suas aplicações. 12 ed. São Paulo:

Editora Atlas, 2012.

CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.

MARQUEZAN, L. H. F.; BRONDANI, G. Análise de investimentos. Revista eletrônica de contabilidade, v. 3, n. 1, p. 35-35, 2006.

PADOVEZE, C. L. Contabilidade gerencial: um enfoque em sistema de informação contábil. 4 ed. São Paulo: Atlas, 2004.

Determinação da taxa de juros do valor futuro

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você aprofundará ainda mais seu conhecimento sobre os investimentos, sejam eles para compra de um veículo, um imóvel, entre outros. Você vai também compreender sobre como calcular o valor da taxa de juros imposta em um rendimento e fazer uso da calculado HP – 12C para seu cálculo. 
Para melhor compreender sobre o assunto, imagine que o dono de uma multinacional pretende fazer uma reforma, mas para isso vai aplicar R$ 10.000,00 por mês, durante seis meses. Sabendo que essa mesma aplicação resultou, num período de quatro meses, no valor de R$ 48.763,64, depositando R$ 12.000,00 por mês, qual é a taxa de juros dessa aplicação?
Para isso, vamos dar início ao nosso estudo!

Vamos Começar!

Taxa de juros no investimento

Quando estamos pensando em fazer um investimento, é necessário estar ciente da influência do cenário econômico, assim como a taxa de juros também pode impactar diretamente a sua estrutura. Além disso, a taxa de juros é bastante utilizada no mercado de crédito como um todo, por esse motivo é importante estar atento às suas variações.
Compreender e conseguir determinar a taxa de juros pode contribuir para melhores resultados nas aplicações financeiras, já que ela afeta de maneira direta a rentabilidade da maioria dos investimentos disponibilizados no mercado. 
Um exemplo disso pode ser de duas financeiras oferecendo taxas de juros distintas; mesmo que o valor da diferença entre ela seja pequeno, opte sempre pela menor e as melhores condições, pois isso pode impactar o seu rendimento futuro. 

Siga em Frente...

Métodos para o cálculo de taxa

Muitas vezes necessitamos determinar a taxa imposta em investimentos. Nesse caso, podemos fazer uso do Método de Newton-Raphson para valor futuro, o qual apresenta o menor número de iterações. Para sua aplicação, fazemos uso de uma série de funções, em que:

• VF: valor futuro
• parc: valor do depósito periódico e igual
• $i_j$: taxa de juros (chute)

 

Função da taxa de juros compostos:

$f{(i}_j)=\frac{VF}{dep}{i}_j-{\left(1+i_j\right)}^n+1$

Função marginal da taxa de juros compostos:

$f{\mathrm{\text{'}}(i}_j)=\frac{VF}{dep}-{n\left(1+i_j\right)}^{n-1}$

Função de Newton-Raphson:

$i_{j+1}=i_j-\frac{f\left(i_j\right)}{f\mathrm{\text{'}}\left(i_j\right)}$

Mecanismo do método:
1º passo: estipular uma taxa de juros compostos inicial em valor relativo $\left(i_j\right)$.
2º passo: substituir $i_j$ na função da taxa de juros compostos $f\left(i_j\right)$.

Se $\left|f\left(i_j\right)\right|\le \mathrm{0,0001}$, então $i_j$ é a taxa de juros compostos imposta na aplicação.

Se $\left|f\left(i_j\right)\right|>\mathrm{0,0001}$, então $i_j$ não é a taxa de juros compostos imposta na aplicação, vá para o 3º passo.

3º passo: usando o valor da taxa de juros compostos $i_j$, calcule o valor da função marginal da taxa de juros compostos $f\mathrm{\text{'}}\left(i_j\right)$.

4º passo: usando os valores da taxa de juros compostos $\left(i_j\right)$, da função da taxa de juros compostos $f\left(i_j\right)$ e da função marginal da taxa de juros compostos $f\mathrm{\text{'}}\left(i_j\right)$, calcule a próxima taxa de juros compostos $\left(i_{j+1}\right)$, que deverá substituir a última taxa que não deu certo.

5º passo: com a nova $(i_{(}j+1))$ determinada no passo anterior, volte ao 2º passo e refaça os cálculos como se essa fosse a taxa inicial, esquecendo-se da taxa anterior.

Os passos deverão ser repetidos até que:

$\left|f\left(i_j\right)\right|\le \mathrm{0,0001}$

Exemplo disso é quando pretende saber qual o valor dos depósitos periódicos e iguais, as quantidades das parcelas e o resultado da aplicação.

 

Utilização da calculadora HP para cálculo da taxa de investimento

Além do método de Newton-Raphson podemos calcular a taxa de um investimento com depósitos iguais e periódicas a partir da utilização da calculadora HP-12C. 
Observe o passo a passo na HP12C para cálculo da taxa de juros num financiamento.

• Digita valor futuro → Tecla CHS e Tecla FV
• Digita quantidade de depósitos → Tecla n
• Digita valor do depósito → Tecla PMT
• Tecla i

Observe um exemplo:
João Lucas depositou todos os meses, durante 15 meses, o valor de R$ 2.000,00 em um investimento. Esse investimento resultou um montante final de R$ 34.586,83. Qual é a taxa de juros compostos paga por essa aplicação?
Podemos seguir o passo a passo abaixo para resolver pela HP12C:

• Digita o valor futuro → 34 586,83 → Tecla CHS e Tecla FV
• Digita quantidade de depósitos → 15 → Tecla n
• Digita valor do depósito → 2 000→ Tecla PMT
• Tecla i

Logo, teremos o valor da taxa igual a 2% a.m.

Vamos Exercitar?

Para colocar em prática os conceitos vistos, imagine que o dono de uma multinacional pretende fazer uma reforma, mas para isso vai aplicar R$ 10.000,00 por mês, durante seis meses. Sabendo que essa mesma aplicação resultou, em um período de quatro meses, o valor de R$ 48.763,64, depositando R$ 12.000,00 por mês, qual é a taxa de juros dessa aplicação?
1ª Etapa: determinando a taxa de juros compostos da aplicação:

$VF:R\$\mathrm{48.763,64}$

$i_j$: Taxa de juros compostos que desejamos encontrar.

n: 4

dep: R$ 12.000,00/mês

Substituindo na função da taxa de juros compostos, temos?

$f\left(i_j\right)=\frac{VF}{dep}{i}_j-{\left(1+i_j\right)}^n+1$

$f\left(i_j\right)=\frac{\mathrm{48.763,64}}{12.000}{i}_j-{\left(1+i_j\right)}^4+1$

$f\left(i_j\right)=\mathrm{4,0636}{i}_j-{\left(1+i_j\right)}^4+1$

Substituindo na função da taxa de juros compostos

$f\text{'}\left(i_j\right)=\frac{VF}{dep}-n{\left(1+i_j\right)}^{n-1}$

$f\text{'}\left(i_j\right)=\mathrm{4,0636}-4{\left(1+i_j\right)}^3$

Substituindo na função da taxa de juros compostos

$i_{j+1}=i_j-\frac{f\left(i_j\right)}{f\text{'}\left(i_j\right)}$

Observe na tabela como fica as iterações:

 

	1º	2º	3º	4º
Iterações	$i_j$	$F\left(i_j\right)$	$F’\left(i_j\right)$	$i_{j+1}$
1ª	0,02	-0,0012	-0,1812	0,0134
2ª	0,0134	-0,0002	-0,0992	0,0114
3ª	0,0114	-0,0001 FIM	9,0687	0,0100

Logo, a taxa imposta nesse investimento é de 1,14% a.m.

Saiba Mais

Para saber mais sobre investimentos, leia a dissertação O efeito dos atributos dos mercados na escolha de investimentos de Simone Hilário da Silva Brasileiro.

Referências Bibliográficas

ASSAF NETO, A. Matemática financeira e suas aplicações. 12. ed. São Paulo:

Editora Atlas, 2012.

BRASILEIRO, S. H. S. et al. O efeito dos atributos dos mercados na escolha de investimentos. 2018.

CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.

PADOVEZE, C. L. Contabilidade gerencial: um enfoque em sistema de informação contábil. 4 ed. São Paulo: Atlas, 2004.

Amortização

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você conhecerá sobre os sistemas de amortização para financiamentos, seja de um imóvel, um carro, entre outros. Abordaremos suas principais características, assim como vamos aprender a realizar cálculos para o sistema SAC e PRICE.  
Para melhor compreender sobre o assunto, imagine que você vai financiar uma obra em 4 parcelas trimestrais sob regime de juros compostos e taxa de 3,66% a.t. Sabendo que o sistema de amortização é o SAC e o valor financiado é de R$ 306.000,00, qual valor das parcelas? 
Para isso, vamos dar início ao nosso estudo!

Vamos Começar!

Sistemas de amortização

É muito comum as pessoas optarem por financiamentos para compra da sua casa própria, carro, para realizar uma viagem, algum item para sua casa, entre outros. Muito se discute sobre valores abusivos de juros que podem ser cobrados em alguns financiamentos, por isso é necessário conhecer e compreender os tipos de financiamentos para optar pelo melhor cenário. 
No Brasil, para financiamentos, de uma forma geral, podemos utilizar diversos métodos, mas em específico, nesta aula, abordaremos sobre os dois métodos de amortização da dívida de compra: 

• SAC (Sistema de Amortização Constante).
• PRICE (Sistema Francês de Amortização).

Um exemplo desses métodos pode ser o financiamento de uma casa pela SAC e um carro pelo sistema PRICE.

Siga em Frente...

Sistema SAC

O SAC - Sistema de Amortização Constante tem como característica a diminuição do valor das parcelas ao longo do tempo. Para o cálculo de suas parcelas temos que primeiramente calcular o valor da amortização, pois a parcela será composta sempre pela mesma amortização, afinal ela é constante, mais o valor dos juros. 

 

• Fórmula para cálculo da Amortização $A_m$

$Am=\frac{VP}{n}$

Em que,

• Am: Amortização
• VP: Valor presente
• n: Quantidade parcelas
   
• Fórmula para cálculo da Parcela $P_k$

$P_k=Am+J_k$

Em que,

• Am: amortização
• $P_k$: valor da parcela
• $J_k$: juros
   
• Fórmula para cálculo dos Juros $J_k$

$J_k=D_{k-1}.i$

Em que,

$J_k$: juros

$D_{k-1}$: dívida anterior

i: taxa de juros

 

• Fórmula para cálculo da Dívida $D_k$

$D_{k+1}=D_k-Am$

Em que,

• $D_{(}k+1)$: dívida atual
• $D_k$: dívida
• Am: amortização

Um exemplo desse tipo de sistema é para financiamento de compra de imóveis.

 

Sistema PRICE

O PRICE – Sistema Francês de Amortização tem como característica suas parcelas serem iguais. Tem maior aplicação em financiamentos de veículos.

Fórmula para cálculo da Parcela: 

$parc=\frac{VP.i.{(1+i)}^n}{{(1+i)}^n-1}$

Em que,

• parc: valor da parcela
• VP: valor presente
• n: quantidade parcelas
• i: taxa de juros

Fórmula para cálculo da Amortização $A_m$

${Am}_k=parc-J_k$

Em que,

• Amk: amortização
• parc: valor da parcela
• $J_k$: valor dos juros
   

Fórmula para cálculo dos Juros $J_k$

$J_k=D_{k-1}.i$

Em que:

• $J_k$: juros
• $D_{k-1}$: dívida anterior
• I: taxa de juros

Fórmula para cálculo da Dívida $D_k$

$D_k=D_{k-1}-{Am}_k$

Em que,

• $D_{k-1}$: dívida anterior
• $D_k$: dívida
• Amk: amortização

Um exemplo desse tipo de método são financiamentos de veículos, em que as parcelas são constantes ao longo de todo financiamento.

Vamos Exercitar?

Para colocar em prática os conceitos vistos, imagine que você vai financiar uma obra em 4 parcelas trimestrais sob regime de juros compostos e taxa de 3,66% a.t. Sabendo que o sistema de amortização é o SAC e o valor financiado é de R$ 306.000,00, qual valor das parcelas? 

Dívida ($D_k$) $D_{k+1}=D_k-Am$	Amortização (Am) $Am=\frac{VP}{n}$	Juros ($J_k$) $J_k=D_{k-1}.i$	Parcela ($P_k$) $P_k={Am+\mathrm{ }J}_k$
306 000,00	76 500,00
229 500,00	76 500,00	11 199,60	87 699,60
153 000,00	76 500,00	8 399,70	84 899,70
76 500,00	76 500,00	5 599,80	82 099,80
0,00	76 500,00	2 799,90	79 288,90
	306 000,00		333 999,00

Para melhor compreender a nossa tabela:

• Observe que a nossa dívida inicial $D_k$=306 000.
• Para calcularmos a amortização (coluna II), dividimos o valor do financiamento por R$ 306.000,00 pela quantidade de parcelas (4).
• Na terceira coluna, temos que o cálculo dos juros será a multiplicação da dívida anterior pela taxa de juros. 
• E, por fim, na quarta coluna, somamos a amortização e valor dos juros para determinação do valor das parcelas. 

Sendo assim, o valor das parcelas será R$ 87.699,60; R$ 84.899,70; R$ 82.099,80; R$ 79.288,90; R$ 333.999,00.

Saiba Mais

Para saber mais sobre financiamentos, leia o artigo SAC ou PRICE? de Debora Borges Ferreira. 

Referências Bibliográficas

ASSAF NETO, A. Matemática financeira e suas aplicações. 12 ed. São Paulo: Editora Atlas, 2012.
CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.
FERREIRA, D. B. Sac ou PRICE? Revista do Professor de Matemática, n. 85, p. 42-45, SBM, Rio de Janeiro, 2014.
FERNANDES, N. C. C. Matemática financeira: uma abordagem sobre financiamentos. 2014. Disponível em: https://repositorio.ufc.br/handle/riufc/9588. Acesso em: 18 nov. 2023. 
PADOVEZE, C. L. Contabilidade gerencial: um enfoque em sistema de informação contábil. 4 ed. São Paulo: Atlas, 2004.
 

Método Hamburguês

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você aprenderá sobre o cheque especial, bem como utilizar o método hamburguês para calcular valor de juros do cheque especial. Para melhor compreender sobre o tema, imagine que você controla todo fluxo de caixa de uma empresa. Observe o extrato bancário:

Data	Histórico	Movimento	Saldo
01	Transporte		1.000,00 +
03	Clientes	400.000,00 +
05	Fornecedores	150.000,00 -
05	Funcionários	100.000,00 -
10	Encargos fiscais	170.000,00 -
13	Clientes	50.000,00 +
15	Pagamento de reforma	17.541,51 -
22	Pagamento de manutenção	20.000,00 -
28	Pagamento de material de construção	85.000,00 -
30	Clientes	100.000,00 +
30	Juros do cheque especial

A instituição bancária cobra uma taxa de juros simples de 0,47% a.d. e IOF de 0,07% ao dia. Qual o valor dos juros a serem cobrados pelo uso do cheque especial e o saldo bancário da empresa no último dia do mês?
Para isso, vamos dar início ao nosso estudo!

Vamos Começar!

Conta garantida

Muitas pessoas acabam tendo dúvidas sobre o que é uma conta garantida, pois trata-se de um empréstimo rotativo destinado às empresas clientes da instituição financeira. O dinheiro fica disponível da conta bancária do cliente e a empresa, de acordo com o limite contratado, pode fazer seu uso para suprir eventuais necessidades de fluxo de caixa.
Porém, quando o dinheiro é utilizado, são cobrados valores de juros que incidem somente sobre os valores utilizados nos dias úteis, sendo debitados mensalmente da conta garantida e o limite utilizado pode ser coberto a qualquer momento, por meio de créditos na conta garantida.
Podemos dizer que a conta garantida é quase a mesma coisa que cheque especial, com a diferença que conta garantida é um produto específico para pessoas jurídicas. É comum também, na pessoa jurídica, que a conta garantida seja separada da conta da pessoa física. 
Um exemplo de conta garantida é quando uma empresa faz uso do dinheiro disponibilizado pela instituição bancária para pagamentos de salários e depois de alguns dias cobre esse dinheiro e mais o adicional dos juros pelo período utilizado.

Siga em Frente...

Cheque especial

Hoje em dia, com tantos imprevistos, muitas vezes, o nosso dinheiro não é suficiente para sanar as despesas do mês, bem como podem aparecer alguns gastos de emergência. Diante desse contexto, o cheque especial é um tipo de crédito que o banco disponibiliza em sua conta corrente, como se fosse um empréstimo pré-aprovado que fica ali disponível diretamente na conta para usar a qualquer momento.  
Algumas instituições bancárias também oferecem um período no qual aquele limite disponível pode ser utilizado sem a aplicação de juros, por até 10 dias sem incidência de juros. 
A partir do cheque especial, o limite fica disponível para usar sempre que a pessoa precisar, fácil e prático, mas é necessário cautela, pois muitas pessoas cometem o erro de usar o limite do cheque especial como se fosse uma extensão da conta corrente, o que pode ocasionar num endividamento fora do controle.
 

Cálculo dos juros do cheque especial

Com intuito de contribuir para o cálculo dos juros do uso do cheque especial e da conta garantida, a serem cobrados ao final de um período de trinta dias para conta garantida ou cheque especial, podemos utilizar o método hamburguês a partir da seguinte fórmula:

$J=(i+IOF)\sum SD.d$

Em que,

• J: juros a serem cobrados pelo uso da conta garantida ou cheque especial.
• i: taxa de juros simples ao dia.
• IOF: Imposto sobre Operações Financeiras ao dia.
• SD: saldo devedor.
• d: número de dias em que o saldo devedor (SD) não se altera.
   

Vamos Exercitar?

Para colocar em prática os conceitos vistos, imagine que você controla todo fluxo de caixa de uma empresa. Observe o extrato bancário:

Data	Histórico	Movimento	Saldo
01	Transporte		1.000,00 +
03	Clientes	400.000,00 +
05	Fornecedores	150.000,00 -
05	Funcionários	100.000,00 -
10	Encargos fiscais	170.000,00 -
13	Clientes	50.000,00 +
15	Pagamento de reforma	17.541,51 -
22	Pagamento de manutenção	20.000,00 -
28	Pagamento de material de construção	85.000,00 -
30	Clientes	100.000,00 +
30	Juros do cheque especial

A instituição bancária cobra uma taxa de juros simples de 0,47% a.d. e IOF de 0,07% ao dia. Qual o valor dos juros a serem cobrados pelo uso do cheque especial e o saldo bancário da empresa no último dia do mês?
Ao analisar o extrato bancário, vamos adicionar os valores positivos, subtrair os valores negativos e quando o saldo ficar negativo multiplicar cada valor pela quantidade de dias que o saldo se manteve negativo.
Sendo assim, temos que:

$\sum \mathrm{SD}.\mathrm{d}=279 \mathrm{364,08}$
$\mathrm{i}=\mathrm{0,47}\% a.d=\mathrm{0,0047} a.d$

$\mathrm{IOF}=\mathrm{0,07}\% \mathrm{a}.\mathrm{d}=\mathrm{0,0007}\mathrm{ }\mathrm{a}.\mathrm{d}$

Substituindo os valores na fórmula:

$\mathrm{J}=(\mathrm{i}+\mathrm{IOF})\sum \mathrm{SD}.\mathrm{d}$

$\mathrm{J}=\left(\mathrm{0,0047}+\mathrm{0,000}\text{7 }\right).\mathrm{279364,08}$

$\mathrm{J}=\mathrm{0,0047.279364,08}$

$\mathrm{J}=\mathrm{R}\mathrm{\$}\mathrm{1.313,01}$

Logo, os juros a serem cobrados serão de R$ 1.313,01.

Saiba Mais

Para saber mais sobre conta garantida e cheque especial, leia o artigo Gestão do capital de giro de pequenas empresas de Valdineide Santos Araújo.

Referências Bibliográficas

ARAÚJO, V. S.; MACHADO, M. A. V. Gestão do capital de giro de pequenas empresas. Revista Ciências Administrativas, v. 13, n. 1, 2007.
ASSAF NETO, A. Matemática financeira e suas aplicações. 12 ed. São Paulo: Editora Atlas, 2012.
CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.
PADOVEZE, C. L. Contabilidade gerencial: um enfoque em sistema de informação contábil. 4 ed. São Paulo: Atlas, 2004.

Videoaula de Encerramento

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Chegada

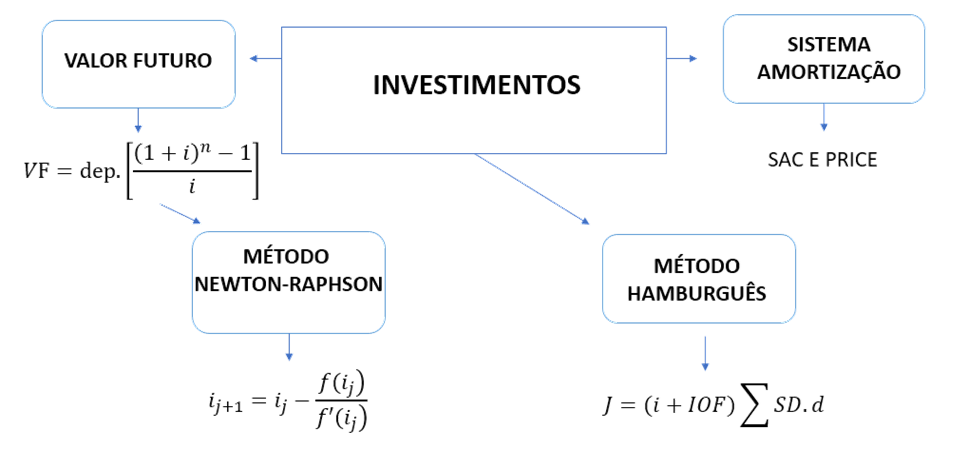
Para desenvolver a competência desta unidade, que é compreender os conceitos relacionados a investimentos e os diferentes tipos sistemas de amortização a fim de aplicá-los na resolução de problemas financeiros, é necessário abordar os seguintes conceitos:
Ao trabalharmos com investimentos com depósitos iguais e periódicos, podemos utilizar o cálculo do valor futuro, a partir da seguinte fórmula matemática:

$V\mathrm{F}=\mathrm{dep}.\left[\frac{{(1+i)}^n-1}{i}\right]$

Em que:

• VF: valor futuro; resultado da aplicação ou investimento.
• dep: refere-se ao valor do depósito.
• n: número total de depósitos periódicos e iguais.
• i: taxa de juros compostos. 
   

Além dessa fórmula do valor futuro, às vezes precisamos determinar a taxa imposta em investimentos. Nesse caso, podemos fazer uso do Método de Newton-Raphson:

• VF: valor futuro.
• parc: valor do depósito periódico e igual.
• $i_j$: taxa de juros (chute).

Função da taxa de juros compostos:

$f{(i}_j)=\frac{VF}{dep}{i}_j-{\left(1+i_j\right)}^n+1$

Função marginal da taxa de juros compostos:

$f{\mathrm{\text{'}}(i}_j)=\frac{VF}{dep}-{n\left(1+i_j\right)}^{n-1}$

Função de Newton-Raphson:

$i_{j+1}=i_j-\frac{f\left(i_j\right)}{f\mathrm{\text{'}}\left(i_j\right)}$

Mecanismo do método

• 1º passo: estipular uma taxa de juros compostos inicial em valor relativo $\left(i_j\right)$.
• 2º passo: substituir i_j  na função da taxa de juros compostos $f\left(i_j\right)$.
  • Se $\left|f\left(i_j\right)\right|\le \mathrm{0,0001}$, então $i_j$ é a taxa de juros compostos imposta na aplicação.
  • Se $\left|f\left(i_j\right)\right|>\mathrm{0,0001}$, então $i_j$ não é a taxa de juros compostos imposta na aplicação, vá para o 3º passo.
• 3º passo: usando o valor da taxa de juros compostos $i_j$, calcule o valor da função marginal da taxa de juros compostos $f\mathrm{\text{'}}\left(i_j\right)$.
• 4º passo: usando os valores da taxa de juros compostos $\left(i_j\right)$, da função da taxa de juros compostos $f\left(i_j\right)$, e da função marginal da taxa de juros compostos $f\mathrm{\text{'}}\left(i_j\right)$, calcule a próxima taxa de juros compostos (i_(j+1) ), que deverá substituir a última taxa que não deu certo.
• 5º passo: com a nova $(i_{(}j+1))$ determinada no passo anterior, volte ao 2º passo e refaça os cálculos como se essa fosse a taxa inicial, esquecendo-se da taxa anterior. 

Os passos deverão ser repetidos até que: 

$\left|f\left(i_j\right)\right|\le \mathrm{0,0001}$

Além do método de Newton-Raphson podemos calcular a taxa de um investimento com depósitos iguais e periódicas a partir da utilização da calculadora HP-12C. 
Agora, em nosso dia a dia, podemos optar por diversos tipos de financiamentos, dois deles são o SAC e o PRICE. O SAC – Sistema de Amortização Constante tem como característica ter suas parcelas num comportamento decrescente, ou seja, as parcelas diminuem ao longo do tempo. 
Já o PRICE – Sistema Francês de Amortização tem como característica suas parcelas serem iguais. Tem maior aplicação em financiamentos de veículos.
E, por fim, para o cálculo dos juros do uso do cheque especial e da conta garantida, a serem cobrados ao final de um período de trinta dias para conta garantida ou cheque especial, podemos utilizar o método hamburguês a partir da seguinte fórmula:

$J=(i+IOF)\sum SD.d$

Em que,

• J: juros a serem cobrados pelo uso da conta garantida ou cheque especial.
• i: taxa de juros simples ao dia.
• IOF: Imposto sobre operações financeiras ao dia.
• SD: Saldo devedor.
• d: número de dias em que o saldo devedor (SD) não se altera.

É Hora de Praticar!

Agora, você colocará em prática os conceitos vistos nesta unidade. Vamos lá!
Carlos pretende realizar uma viagem cujo custo é de R$ 6.400,00. Ele tem R$ 450,00 para aplicar mensalmente num investimento, que paga uma taxa de juros compostos de 1,07% a.m. Sendo assim, quantos depósitos mensais deverão ser feitos para atingir o valor da viagem? 

Reflita

Ao final dos estudos, responda:

• Você consegue identificar qual fórmula utilizar em casa situação problema?
• Você extrai as informações dos problemas de forma correta?
• Você consegue identificar situações do seu dia a dia em nossa disciplina e como ela pode te ajudar?

Dê o Play!

Clique aqui para acessar os slides do Dê o play!

Resolução do estudo de caso

Primeiramente, vamos extrair as informações do problema:
VF: R$ 6.400,00
dep: 400,00
n: ?
i: 1,07% a.m = 0,0107 a.m
Substituindo os valores na fórmula, temos:

$VF=dep\left[\frac{{\left(1+i\right)}^n-1}{i}\right]$

$6400=450\left[\frac{{\left(1+\mathrm{0,0107}\right)}^n-1}{\mathrm{0,0107}}\right]$

$\frac{6400}{450}=\left[\frac{{\left(\mathrm{1,0107}\right)}^n-1}{\mathrm{0,0107}}\right]$

$\mathrm{14,22}.\mathrm{ }\mathrm{0,0107}+1={\left(\mathrm{1,0107}\right)}^n$

$\mathrm{1,1522}={\left(\mathrm{1,0107}\right)}^n$

Para tombar expoente, vamos multiplicar por ln

$ln\mathrm{1,1522}=ln{\left(\mathrm{1,0107}\right)}^n$

$ln\mathrm{1,1522}=n.ln\mathrm{1,0107}$

$\mathrm{0,1417}=n.\mathrm{0,0106}$

$n=\frac{\mathrm{0,1417}}{\mathrm{0,0106}}=\mathrm{13,37}$

Logo, serão necessários aproximadamente 13 meses de depósitos para atingir o valor necessário para a viagem. 

Dê o play!

Assimile

Referências

ARAÚJO, V. S.; MACHADO, M. A. V. Gestão do capital de giro de pequenas empresas. Revista Ciências Administrativas, v. 13, n. 1, 2007.

ASSAF NETO, A. Matemática financeira e suas aplicações. 12 ed. São Paulo:

Editora Atlas, 2012.

CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.

MOREIRA, Fernando Ricardo et al. Juros: conceitos e aplicações. Enciclopédia Bioesfera, v. 6, n. 9, 2010.

OLIVEIRA, W. Sistema de juros compostos. Revista Processus Multidisciplinar, v. 1, n. 1, p. 11-22, 2020.