Estatística Descritiva

Introdução à estatística descritiva

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Você provavelmente já foi abordado em algum momento, seja pessoalmente ou por telefone, para participar de uma pesquisa sobre um tema específico. A disciplina matemática que se concentra na condução de pesquisas e na análise dos dados obtidos é conhecida como Estatística. Nesta aula, exploraremos o significado da Estatística e sua relevância em diversas áreas. Além disso, abordaremos os principais conceitos da Estatística Descritiva, como amostragem, população e variáveis. Esses conceitos formam a base para a compreensão de outros tópicos relacionados à Estatística.

Com o intuito de ilustrar como esses conceitos podem ser aplicados, considere o seguinte cenário: imagine que uma empresa de telefonia contratou você para conduzir uma pesquisa de satisfação entre os clientes em relação aos serviços prestados. A empresa conta com um total de 650 mil clientes, dos quais 45% são mulheres, e o restante são homens. Sua tarefa é desenvolver um guia para a coleta de dados, levando em consideração que você pretende realizar a pesquisa por meio de uma amostragem estratificada proporcional, com amostra de composta de 150 mil clientes.

Como podemos realizar essa coleta de dados? Como podemos definir quantos homens e quantas mulheres participarão da pesquisa?

Vamos começar nossos estudos!

Vamos Começar!

Você pode se indagar: o que exatamente é a Estatística? Por que é importante estudar Estatística? De que maneira a Estatística pode beneficiar minha carreira? Segundo Larson e Farber (2015, p. 3), a “Estatística é a disciplina que coleta, organiza, analisa e interpreta dados para embasar a tomada de decisões”. Esses dados representam informações que adquirimos por meio de observações, experimentos, pesquisas e outros meios. Podemos afirmar que a Estatística tem como propósito investigar fenômenos coletivos, permitindo-nos efetuar julgamentos informados e tomar decisões em face de incertezas e variações. Devore (2018) enfatiza que, na ausência dessas incertezas e variações inerentes a diversos fenômenos, haveria uma escassa necessidade de empregar métodos estatísticos.

Os métodos estatísticos são fundamentais para a determinação de diferentes indicadores, como indicadores de desenvolvimento sustentável. Estes são publicados pelo Instituto Brasileiro de Geografia e Estatística (IBGE) e fornecem informações que possibilitam o acompanhamento da sustentabilidade do padrão de desenvolvimento brasileiro em diferentes dimensões, dentre elas a ambiental. Nesse sentido, os indicadores oferecem “um panorama abrangente de informações necessárias ao conhecimento da realidade do País, ao exercício da cidadania e ao planejamento e formulação de políticas públicas para o desenvolvimento sustentável” (IBGE, 2015, p. 9). Perceba que a Estatística desempenha uma função significativa na tomada de decisões, portanto pode ser uma ferramenta valiosa para você na condução de pesquisas e na investigação de fenômenos em sua futura carreira.

Quando nos referimos à Estatística, podemos dividi-la em dois ramos: Estatística Descritiva e Estatística Inferencial. O primeiro tem como objetivo descrever os dados observados, enquanto o segundo busca obter e generalizar conclusões para a população com base em uma amostra. Inicialmente, direcionaremos nossa atenção para os princípios associados à Estatística Descritiva. Entre os conceitos essenciais incluem-se população, amostra, rol de dados, parâmetros e estimadores.

Podemos dizer que a população é o conjuntos de todos os dados que interessam no estudo e têm alguma característica em comum. Já a amostra é uma parte dessa população, é um subconjunto. Para ilustrarmos como diferenciarmos uma população de uma amostra, considere o exemplo a seguir.

Exemplo 1

Uma empresa de educação encomendou uma pesquisa de opinião para saber qual seria a área do conhecimento mais requisitada na região metropolitana de São Paulo, em 2015.

A pesquisa foi feita com jovens sem nenhuma formação universitária. A empresa de educação pediu que fossem entrevistadas pelo menos 4 mil pessoas. Dos entrevistados, 55% tinham curso universitário, por isso não responderam à pergunta. Ao restante foi feita a seguinte pergunta: Qual é a área de conhecimento que você gostaria de estudar em 2015?

(  ) Exatas      (  ) Humanas    (  ) Saúde       (  ) Gestão

Nesse exemplo, o tamanho da população são os 4 mil entrevistados, e a amostra é composta apenas daqueles que responderam à pergunta; isto é, 45% das 4 mil pessoas, o que corresponde a 1,8 mil pessoas.

Dentre os conceitos estatísticos temos que o parâmetro é uma característica numérica estabelecida para toda a população, enquanto o estimador é uma característica numérica estabelecida para a amostra. Os dados representam todas as informações coletadas. Quando se trata de um conjunto de dados numéricos não ordenados, ou seja, aqueles dados obtidos diretamente da observação de fenômenos, referimo-nos a eles como dados brutos. Por sua vez, quando ordenamos esses dados brutos de maneira crescente ou decrescente, temos o que denominamos rol de dados.

Ao realizarmos uma pesquisa, estamos interessados apenas em determinadas características da população; por exemplo, o número de filhos de uma família. A essas características da população damos o nome de variável. É importante salientar que a característica pode mudar de um objeto para outro na população. De acordo com Devore (2018), os dados são resultantes da observação de uma variável ou de duas ou mais variáveis. Chamamos de conjunto de dados univariado aquele resultante da observação de uma única variável. Quando o conjunto de dados resulta da observação de duas variáveis, é denominado bivariado.

Dependendo da natureza dessas características, é possível classificar uma variável como qualitativa ou quantitativa. As variáveis qualitativas são aquelas que fornecem dados de natureza não numérica, como cor dos olhos ou raça de um animal. Esse tipo de variável pode ser nominal ou ordinal. As variáveis qualitativas ordinais representam categorias ou grupos de dados que apresentam uma ordem intrínseca, mas a diferença entre os valores não é uniforme ou mensurável. Em outras palavras, as categorias em uma variável qualitativa ordinal têm uma relação de ordem, mas não é possível determinar com precisão a magnitude das diferenças entre elas. Um exemplo desse tipo de variável é o nível de escolaridade: ensino fundamental, ensino médio, ensino superior, pós-graduação. Já as variáveis qualitativas nominais são aquelas sem nenhuma ordenação, como cor dos olhos ou estado civil.

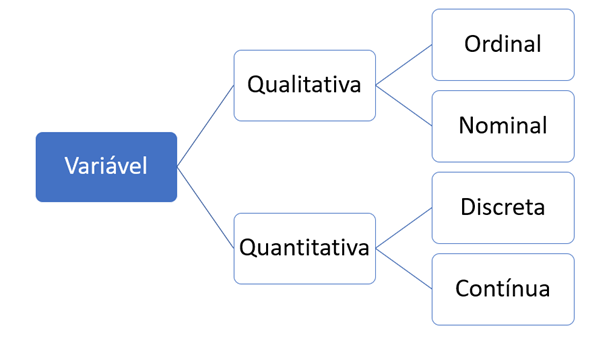
Por outro lado, as variáveis quantitativas são aquelas que podem ser mensuradas por valores numéricos; podem ser de dois tipos: contínuas ou discretas. O primeiro grupo é composto daquelas cujos possíveis valores pertencem a um intervalo de números reais e resultam de uma mensuração, como peso e altura. Já as variáveis quantitativas discretas são aquelas cujos possíveis valores formam um conjunto finito ou enumerável de números e que resultam, frequentemente, de uma contagem, como número de filhos ou número de espécies que vivem em determinado hábitat. A Figura 1 resume os tipos de variáveis.

Siga em Frente...

Um fato importante a se destacar é que grande parte das pesquisas estatísticas são feitas com base em amostras. A utilização de amostras em pesquisas estatísticas oferece algumas vantagens, como a economia de tempo e recursos, visto que coletar dados de toda a população pode ser demorado e dispendioso e usar amostras permite que os pesquisadores coletem informações representativas de maneira mais eficiente e econômica.

É crucial que a amostragem seja realizada de maneira adequada, com um método que minimize o viés e represente de forma precisa a população de interesse. Caso contrário, os resultados da pesquisa podem ser tendenciosos e pouco confiáveis.

Podemos classificar a amostragem como probabilística ou não probabilística. A amostragem é considerada probabilística quando todos os elementos da população têm uma probabilidade conhecida, não nula, de serem selecionados para a amostra. Caso contrário, quando essa probabilidade não é conhecida ou é igual a zero, a amostragem é considerada não probabilística (Costa Neto, 2006).

Dentre os métodos de amostragem probabilística, encontramos:

• Amostragem aleatória simples: realizada por meio de sorteio. Nesse tipo de amostragem, todos os elementos da população têm igual probabilidade de pertencer à amostra, e todas as possíveis amostras têm também igual probabilidade de ocorrer.
• Amostragem sistemática: quando os elementos da população estão dispostos em uma ordem específica e a seleção dos elementos da amostra é realizada de maneira periódica. Um exemplo disso é quando, em uma linha de produção, a cada dez itens fabricados, um é retirado para compor uma amostra da produção diária. Para retirar uma amostra sistemática de tamanho $n$ de uma população com elementos, ordenados de 1 até $N$, seguimos os seguintes passos:
  • Dividimos a população em  subgrupos de tamanho $k=\frac{N}{n}$.
  • No primeiro subgrupo, conduzimos um sorteio (amostragem aleatória simples) para escolher o primeiro elemento que fará parte da amostra. Vamos supor que esse elemento esteja na posição $p\le k$.
  • A partir do sorteio do passo anterior, os demais $n – 1$ elementos pertencentes à amostra ficam determinados. Serão aqueles que estiverem nas posições: $p + k$, $p + 2k$, $p + 3k$, $\dots$, $p +(n – 1)k$.
• Amostragem aleatória estratificada: a população é dividida em subgrupos distintos, chamados estratos, com base em características compartilhadas. Em seguida, uma amostra é selecionada aleatoriamente em cada estrato, de modo que todos os estratos estejam representados na amostra final. Geralmente, na amostragem aleatória estratificada, o tamanho da amostra retirada de cada estrato é correspondente ao percentual que o estrato representa em relação à população.
• Amostragem por conglomerados: divide a população em subgrupos cujos elementos sejam heterogêneos. Cada subgrupo definido nesse tipo de amostragem, denominado conglomerado (ou cluster), será semelhante à população, o que implica a semelhança entre os conglomerados. Após a identificação dos conglomerados (primeira etapa), geralmente se recorre à amostragem aleatória simples para determinar quais deles serão incluídos na amostra (segunda etapa). Posteriormente, é realizado um censo em cada conglomerado selecionado (terceira etapa).

Dentre as técnicas de amostragem não probabilística, temos:

• Amostragem a esmo: o amostrador, para tornar o processo mais simples, busca introduzir um elemento de aleatoriedade, embora não necessariamente execute um sorteio com o auxílio de algum dispositivo aleatório confiável.
• Amostragem intencional ou por conveniência: o amostrador deliberadamente escolhe certos elementos para pertencer à amostra, por julgá-los bem representativos da população.

Quando conduzimos uma pesquisa, é essencial definir se examinaremos toda a população ou uma amostra, identificar os tipos de dados analisados e reconhecer os tipos de variáveis em estudo. Ter clareza dessas informações é de suma importância, pois isso determina os métodos estatísticos aplicados na análise dos conjuntos de dados.

Vamos Exercitar?

Uma das etapas mais importantes de toda coleta de dados é o planejamento. Geralmente, ele pode ser feito por meio da determinação de um roteiro ou checklist. Para ter eficiência, esse roteiro deve ser elaborado e revisado a fim de evitar falhas. Ao final, o pesquisador deve conferir se todas as etapas previstas no roteiro foram concluídas. Veja a seguir um possível roteiro para a coleta de dados de nossa pesquisa na empresa de telefonia.

1. Definir o objetivo da pesquisa: determinar a satisfação dos clientes acerca do serviço prestado pela companhia telefônica.
2. Definir as variáveis e a população de interesse: a empresa quer saber apenas a satisfação de seus clientes (variável de interesse), sem outras informações agregadas. A população corresponde a 650 mil clientes da companhia.
3. Definir o sistema de coleta de dados: a técnica de amostragem a ser utilizada é a amostragem estratificada. Para isso, temos que determinar o número de pessoas em cada estrato. Como 45% da população são mulheres, temos que 45% da amostra devem ser mulheres; ou seja, 45% de 150 mil, que correspondem a 67,5 mil mulheres. Por sua vez, 55% da amostra devem ser homens; isto é, 55% de 150 mil, que correspondem a 82,5 mil homens. Posteriormente, retira-se uma amostra em cada estrato, procedimento que pode ser realizado por amostragem aleatória simples. Resta determinar o que será perguntado aos clientes. Assumiremos que será feita pergunta como “Em uma escala de 0 a 10, sendo 0 ruim e 10 ótimo, qual nota o(a) senhor(a) atribuiria ao serviço prestado por esta companhia?”.
4. Coletar os dados: é preciso que os funcionários sejam devidamente capacitados para conduzir os contatos por telefone. É relevante destacar que o treinamento dos entrevistadores desempenha um papel crucial, pois pode influenciar na introdução de vieses.
5. Revisar os dados coletados: se houver particularidades nos dados coletados, é possível revisá-los com base nas gravações telefônicas das entrevistas, sempre que esse recurso estiver acessível.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre os conceitos iniciais da estatística, sugerimos a leitura do capítulo 1 do livro Estatística aplicada. Não deixe de selecionar alguns exercícios desse capítulo e resolvê-los!
Para que você possa resolver exercícios relacionados ao conceito de amostragem, sugerimos a leitura da seção 2.3 (Amostragem) do livro Estatística fácil. Não deixe de selecionar alguns exercícios dessas seções e resolvê-los!

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

IBGE. Coordenação de Recursos Naturais e Estudos Ambientais [e] Coordenação de Geografia. Indicadores de desenvolvimento sustentável. Rio de Janeiro: IBGE, 2015.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

Organização dos dados

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Quando realizamos uma pesquisa estatística, coletamos um conjunto de dados que posteriormente devem ser organizados para análise.

Nesta aula, estudaremos formas de organizar um conjunto de dados; por exemplo, em tabelas e gráficos estatísticos. Veremos as tabelas de frequência, observando o que são frequências absoluta, relativa e acumulada. Além disso, discorreremos sobre como construir as tabelas de frequência (com e sem classe), bem como os diferentes tipos gráficos, explicitando suas principais características.

Para que você compreenda como podemos utilizar esses conceitos, pense na seguinte situação: suponha que uma pesquisa foi realizada para analisar a altura e a idade das árvores de determinada região. Utilizando os instrumentos adequados, foram coletados dados de 40 árvores, conforme mostra a Tabela 1.

Idade (em anos)	Altura (em metros)	Idade (em anos)	Altura (em metros)	Idade (em anos)	Altura (em metros)	Idade (em anos)	Altura (em metros)
1	1	6	5,9	10	9,9	13	13,5
1	1,2	6	6,2	10	10,2	13	13,6
2	3,2	6	6,7	10	10,9	14	14
2	3,3	7	6,9	11	11,1	15	15,3
3	3,4	7	7	11	11,4	15	15,7
3	3,5	7	7,1	12	12,5	15	15,9
4	4,3	8	7,8	12	12,7	18	17,9
4	4,7	8	7,9	12	12, 8	19	18,9
5	4,9	9	8,9	12	12,9	20	19,9
5	5,1	9	9,5	12	13	20	21

Tabela 1 | Dados referentes à altura e à idade de árvores. Fonte: elaborada pela autora.

Com base nesses dados, construa:

1. Tabela de frequência com classe para a variável altura.
2. Histograma e polígono de frequência para a variável altura.

Para resolver esse problema, precisamos entender os conceitos de frequência absoluta, frequência relativa e como podemos construir um histograma.

Bons estudos!

Vamos Começar!

Quando conduzimos uma pesquisa, estamos em busca de respostas para um problema específico. Para isso, coletamos informações, e é crucial que os dados coletados sejam organizados de maneira a facilitar sua análise e compreensão por parte do leitor. Um modo de organizar esses dados é em uma tabela. É importante destacar, ainda, que tabelas e quadros são representações distintas. As tabelas são compostas de linhas dispostas verticalmente e apresentam bordas laterais abertas; normalmente, são usadas para representar dados quantitativos. Por outro lado, os quadros têm suas bordas laterais fechadas e são mais apropriados para representar dados qualitativos.

A tabela de distribuição de frequência ou tabela de frequência é muito utilizada na Estatística e é uma representação tabular que contém as variáveis, a frequência absoluta, a frequência relativa e, em alguns casos, a frequência acumulada. A frequência absoluta ou frequência simples, denotada por $f_a$, é o número de vezes que um dado figura no conjunto de dados. Já a frequência relativa, denotada por $f_r$, é a razão entre a frequência absoluta e a quantidade total de dados. Considerando  a quantidade total de dados, a frequência relativa é dada por $f_r=\frac{f_a}{n}$. Por ser comum denotarmos essa frequência em termos de porcentagem, é necessário multiplicar o resultado por 100. A frequência acumulada, denotada por $f_{ac}$, é a medida de valores até um ponto e não mais de um único valor, isto é, mede a frequência absoluta ou relativa até certo ponto, e não apenas em um valor.

Observe que uma tabela de frequências apresenta os valores observados da variável em estudo e suas respectivas frequências, que podem representar tanto o valor individual quanto valores agrupados. Quando se trata de variáveis quantitativas discretas, geralmente utilizamos tabelas de distribuição de frequência sem agrupamentos; e, quando os dados são contínuos, utilizamos uma tabela de distribuição de frequência com classe. A Tabela 2 mostra um exemplo.

Dia 1	Dia 2	Dia 3	Dia 4	Dia 5	Dia 6	Dia 7	Dia 8	Dia 9	Dia 10
1	2	3	1	1	2	2	2	3	3

Tabela 2 | Número de acidentes em uma rodovia no período de dez dias. Fonte: elaborada pela autora.

 

Note que são dados discretos, então é possível construir uma tabela de frequência sem agrupar os dados em classes. Considerando que a variável estudada é o número de acidentes que ocorrem por dia, veja a Tabela 3.

 

Número de acidentes	Frequência absoluta ${\mathit{f}}_{\mathit{a}}$	Frequência relativa ${\mathit{f}}_{\mathit{r}}$	Frequência acumulada ${\mathit{f}}_{\mathit{a}\mathit{c}}$
1	3	$\frac{3}{10}\cdot 100=30\%$	$30\%$
2	4	$\frac{4}{10}\cdot 100=40\%$	$40\%+30\%=70\%$
3	3	$\frac{3}{10}\cdot 100=30\%$	$30\%+70\%=100\%$

Tabela 3 | Tabela de frequência para o número de acidentes na rodovia. Fonte: elaborada pela autora.

 

Por outro lado, quando temos dados contínuos, podemos utilizar uma tabela de frequência com classe. Para isso é preciso:

• Determinar o número de classes, ou intervalos $\left(k\right)$. Esse número é dado pela raiz quadrada da quantidade de dados $\left(n\right)$, isto é, $k=\sqrt{n}$. O resultado dessa raiz dificilmente dará um número inteiro, assim a quantidade de classes será o maior valor inteiro mais próximo de $\sqrt{n}.$
• Determinar a amplitude total do rol de dados $\left(AT\right)$. Essa amplitude é dada pela diferença entre o maior e o menor valor do conjunto de dados.
• Determinar a amplitude do intervalo de classe $\left(h\right)$. Esse tamanho será dado pela razão entre a amplitude total e o número de classes, isto é, $h=\frac{AT}{K}$.
• Determinar o limite das classes. O limite inferior será o valor mínimo do conjunto de dados, e o limite superior será o limite inferior mais a amplitude do intervalo de classe. Repete-se esse processo até a construção da última classe. Comumente utilizamos os seguintes símbolos para representar a classe: $⊢$ou $⊣$. O símbolo $⊢$ indica que o número à esquerda do traço está incluído no intervalo e o da direita, não. Por sua vez, o símbolo $⊣$indica que o número à direita do traço está incluído no intervalo e o da esquerda, não.
• Determinar frequência absoluta, relativa e acumulada. Para determinar a frequência absoluta, temos que contar quantos são os dados que pertencem ao intervalo de classe.

Siga em Frente...

Essas tabelas de frequência podem ser representadas graficamente por meio dos histogramas. Para sua construção, é necessário considerar se a distribuição de frequência é com ou sem classe. Se a distribuição é sem classe, o histograma é um conjunto de hastes, representadas em um sistema de coordenadas cartesianas, cuja base são os valores das variáveis e altura são valores proporcionais às frequências simples correspondentes desses dados. A Figura 1 ilustra um histograma para uma distribuição de frequência sem classe que consta na Tabela 3.

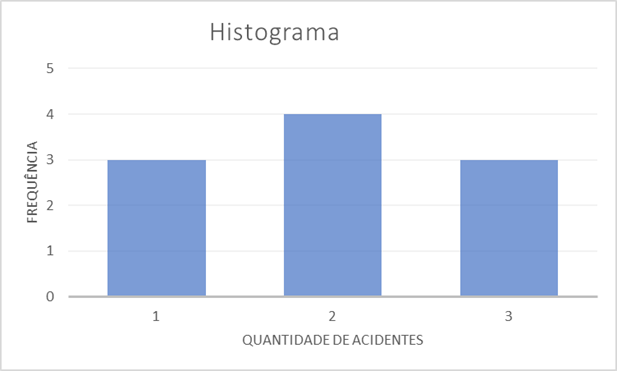
Por outro lado, quando a distribuição de frequência é com classe, as hastes do histograma são justapostas, isto é, não há espaço entre uma haste e outra. Além disso, as bases dessas hastes são os intervalos de classe e a altura, a frequência absoluta relacionada a esses intervalos. O polígono de frequência é construído a partir dos pontos médios de cada classe. Temos que considerar o espaçamento inicial e o final como sendo classes fictícias com frequência zero e unir os pontos médios das bases superiores desses retângulos, obtendo assim um polígono de frequência.

Organizar os dados em tabelas de frequências e gráficos é uma prática fundamental na análise de dados, pois torna as informações mais claras, acessíveis e úteis para a tomada de decisões e uma comunicação eficaz.

Vamos Exercitar?

Vamos retornar à nossa situação inicial e construir uma tabela de frequência com classes. Os dados encontram-se na Tabela 4.

Idade (em anos)	Altura (em metros)	Idade (em anos)	Altura (em metros)	Idade (em anos)	Altura (em metros)	Idade (em anos)	Altura (em metros)
1	1	6	5,9	10	9,9	13	13,5
1	1,2	6	6,2	10	10,2	13	13,6
2	3,2	6	6,7	10	10,9	14	14
2	3,3	7	6,9	11	11,1	15	15,3
3	3,4	7	7	11	11,4	15	15,7
3	3,5	7	7,1	12	12,5	15	15,9
4	4,3	8	7,8	12	12,7	18	17,9
4	4,7	8	7,9	12	12, 8	19	18,9
5	4,9	9	8,9	12	12,9	20	19,9
5	5,1	9	9,5	12	13	20	21

Tabela 4 | Dados referentes à altura e à idade de árvores. Fonte: elaborada pela autora.

 

Antes de começar a construir a tabela de frequência, é necessário verificar se os dados estão organizados em ordem crescente. Caso não estejam, organize-os antes de construir sua tabela de frequência.

a) A fim de elaborarmos nossa tabela de frequência, é essencial determinar o número de classes, a amplitude de cada intervalo de classe, os limites inferiores e superiores de cada intervalo e, por último, calcular as frequências absoluta, relativa e acumulada. O número de classes será definido como a raiz quadrada da quantidade total de dados. Como há 40 dados no exemplo, o número de classes será $\sqrt{40}\cong \mathrm{6,32}$. a)    Por se tratar de um valor não inteiro, consideraremos que o número de classes é o maior inteiro próximo ao valor encontrado, ou seja, sete classes.
O próximo passo é determinar a amplitude do intervalo de classe, o que requer inicialmente a amplitude total do conjunto de dados. O maior valor é 21 e o menor é 1, assim a amplitude total será $AT=21-1=20$. A amplitude do intervalo de classe será dada pela razão entre a amplitude total e o número de classes, ou seja, $h=\frac{20}{7}\cong \mathrm{2,9}$.
Quando o resultado dessa razão não for inteiro, você pode considerar apenas uma casa decimal. Agora temos que construir os limites inferiores e superiores de cada classe, como mostra a Tabela 5.

	Classe 1	Classe 2	Classe 3	Classe 4	Classe 5	Classe 6	Classe 7
Limite Inferior	$1$	$\mathrm{3,9}$	$\mathrm{6,8}$	$\mathrm{9,7}$	$\mathrm{12,6}$	$\mathrm{15,5}$	$\mathrm{18,4}$
Limite superior	$1+\mathrm{2,9}=\mathrm{3,9}$	$\mathrm{3,9}+\mathrm{2,9}=\mathrm{6,8}$	$\mathrm{6,8}+\mathrm{2,9}=\mathrm{9,7}$	$\mathrm{9,7}+\mathrm{2,9}=\mathrm{12,6}$	$\mathrm{12,6}+\mathrm{2,9}=\mathrm{15,5}$	$\mathrm{15,5}+\mathrm{2,9}=\mathrm{18,4}$	$\mathrm{18,4}+\mathrm{2,9}=\mathrm{21,3}$

Tabela 5 | Construção dos limites superiores e inferiores das classes. Fonte: elaborada pela autora.

 

Para os intervalos, utilizaremos o símbolo $⊢$, que significa que o número à esquerda pertence ao intervalo. Para determinar a frequência absoluta, devemos contar quantos dados pertencem a cada intervalo de classe, considerando a simbologia adotada. A frequência relativa será dada pela razão entre a frequência absoluta e a quantidade total de dados. Com base nessas informações, teremos a seguinte tabela de frequência (Tabela 6).

Altura	Frequência absoluta ${\mathit{f}}_{\mathit{a}}$	Frequência relativa ${\mathit{f}}_{\mathit{r}}$	Frequência acumulada ${\mathit{f}}_{\mathit{a}\mathit{c}}$
$1⊢\mathrm{3,9}$	6	$\frac{6}{40}\cdot 100=15\%$	$15\%$
$\mathrm{3,9}⊢\mathrm{6,8}$	7	$\frac{7}{40}\cdot 100=\mathrm{17,5}\%$	$\mathrm{32,5}\%$
$\mathrm{6,8}⊢\mathrm{9,7}$	7	$\frac{7}{40}\cdot 100=\mathrm{17,5}\%$	$50\%$
$\mathrm{9,7}⊢\mathrm{12,6}$	6	$\frac{6}{40}\cdot 100=15\%$	$65\%$
$\mathrm{12,6}⊢\mathrm{15,5}$	8	$\frac{8}{40}\cdot 100=20\%$	$85\%$
$\mathrm{15,5}⊢\mathrm{18,4}$	3	$\frac{3}{40}\cdot 100=\mathrm{7,5}\%$	$\mathrm{92,5}\%$
$\mathrm{18,4}⊢\mathrm{21,3}$	3	$\frac{3}{40}\cdot 100=\mathrm{7,5}\%$	$100\%$

Tabela 6 | Tabela de frequência para a variável altura. Fonte: elaborada pela autora.

 

b) Como temos uma tabela de frequência com classe, as hastes que compõem o histograma devem estar justapostas. Além disso, perceba que a altura começa a partir de 1, então a primeira haste não pode estar colada no eixo y. O histograma para essa tabela de frequência está ilustrado na Figura 2.

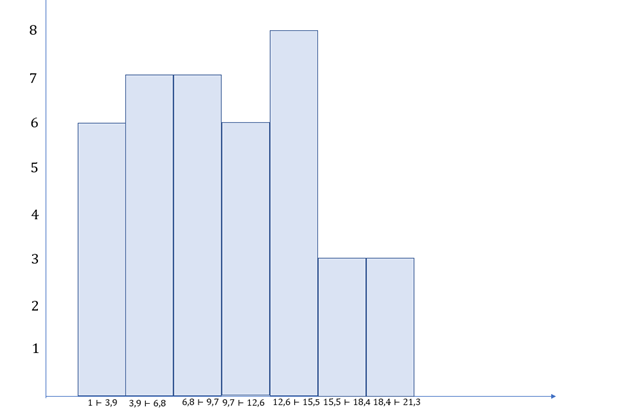
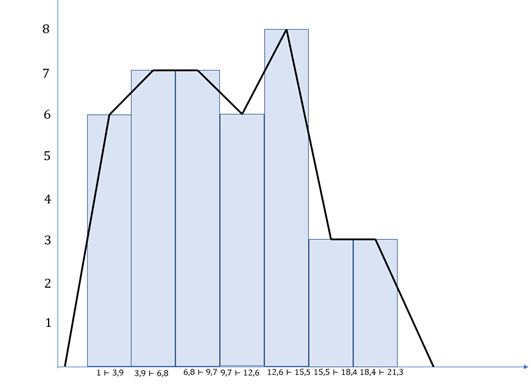
O polígono de frequência será construído a partir do ponto médio de cada classe, conforme ilustra a Figura 3. Observe que a linha que forma o polígono deve começar e finalizar no eixo x.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre a construção de tabelas de frequência e histogramas, sugerimos a leitura do capítulo 2 do livro Estatística. Ao final do capítulo, selecione alguns exercícios e os resolva!

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

Medidas de tendência central

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! A condução de um estudo estatístico exige não apenas a coleta e a estruturação dos dados, mas também a avaliação dessas informações, a qual pode ser realizada por meio da computação de medidas de tendência central.

As três medidas de tendência central mais comuns são a média (ou média aritmética), a mediana e a moda, e cada uma delas tem suas próprias aplicações e interpretações em contextos diferentes. Em resumo, essas medidas desempenham um papel fundamental na análise estatística, ajudando a extrair informações importantes dos dados e a tomar decisões informadas.

Com o intuito de ilustrar como esses conceitos podem ser aplicados, considere que você realizou uma pesquisa em sua turma da faculdade a fim de analisar a altura dos colegas. Os resultados dessa pesquisa encontram-se na Tabela 1.

164	156	165	178	165	180	155	190	167	169
168	176	175	165	166	167	155	165	170	178

Tabela 1 | Dados referentes à altura (cm). Fonte: elaborada pela autora.

 

Com base nesses dados, você quer determinar a altura média dos alunos da turma, bem como a altura mediana e a moda das alturas. Para isso, precisamos entender como calcular essas medidas.

Bons estudos!

Vamos Começar!

Sabemos que a organização de dados por meio de tabelas e gráficos é fundamental em uma pesquisa estatística. Agora, estudaremos uma forma suplementar de apresentar esses dados por meio das medidas da tendência central.

Segundo Larson e Farber (2015, p. 55), “uma medida da tendência central é um valor que representa uma entrada típica ou central do conjunto de dados”. As medidas mais utilizadas são a média, a moda e a mediana. O cálculo dessas medidas pode auxiliar o pesquisador na análise dos dados, pois permite localizar a maior concentração de valores de uma distribuição, ou seja, se os dados se concentram mais no início, no meio ou no final. Logo, essas medidas viabilizam comparações entre conjuntos de dados.

A média aritmética, ou média simples, de um conjunto de dados (não agrupados) é o quociente entre a soma de todos os dados, $x_i$, e a quantidade de dados, $n$:

 $\stackrel{-}{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$

A notação utilizada anteriormente representa a média de uma amostra. Caso estejamos trabalhando com uma população e precisemos determinar a média aritmética, utilizamos o mesmo cálculo, porém a média populacional é representada da seguinte maneira:

$\mu =\frac{1}{n}\sum _{i=1}^n{x}_i$

Agora, exploraremos o processo de cálculo da média por meio do exemplo a seguir.

 

Exemplo 1

Uma equipe de especialistas do centro meteorológico de uma cidade mediu a temperatura do ambiente, sempre no mesmo horário, durante 16 dias intercalados, a partir do primeiro dia de um mês. Esse tipo de procedimento é frequente, visto que os dados coletados servem de referência para estudos e verificação de tendências climáticas ao longo dos meses e anos. As medições desse período estão indicadas na Tabela 2.

Dia do mês	Temperatura °C
1	15,5
3	14
5	13,5
7	18
9	19,5
11	20
13	13,5
15	13,5
17	18
19	20
21	18,5
23	13,5
25	21,5
27	20
29	16
31	21

Tabela 2 | Dados referentes à temperatura do ambiente. Fonte: elaborada pela autora.

 

Vamos determinar a temperatura média. Sabendo que a média é determinada pelo quociente entre a soma de todos os valores e a quantidade total de dados, temos:

$\stackrel{-}{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$

$\stackrel{-}{x}=\frac{1}{16}\left(\mathrm{15,5}+14+\mathrm{13,5}+18+\mathrm{19,5}+20+\mathrm{13,5}+\mathrm{13,5}+18+20+\mathrm{18,5}+\mathrm{13,5}+\mathrm{21,5}+20+16+21\right)$

$\stackrel{-}{x}=\frac{1}{16}\left(276\right)=\frac{276}{16}=\mathrm{17,25}$

Logo, a temperatura média é de 17,25 °C.

Sabemos que a média aritmética de dados não agrupados pode ser calculada dividindo-se a soma de todos os valores pelo número total de dados. É relevante destacar que se houver um valor extremamente discrepante dos demais, a média simples será influenciada por esse valor atípico.

A média aritmética não é o único tipo de média que podemos calcular. Há, por exemplo, a média ponderada, que considera que cada valor tem um peso diferente. Denotando o peso por, $p$, temos que a média ponderada é dada por:

$\stackrel{-}{x_p}=\frac{\sum _{i=1}^n{(x}_i\cdot p_i)}{\sum _{i=1}^n{p}_i}$

Esse tipo de média é muito utilizada no cálculo de notas, conforme mostra o exemplo a seguir.

 

Exemplo 2

Consideremos que um professor decida que haverá dois exames parciais, valendo cada um 30% da nota, e um exame final, valendo 40%. Se um estudante obtém desempenho 70 na primeira avaliação, 65 na segunda e 80 no exame final, a média ponderada das notas será:

${\stackrel{-}{x_p}}_{pond}=\frac{70\cdot \mathrm{0,30}+65\cdot \mathrm{0,30}+80\cdot \mathrm{0,40}}{\mathrm{0,30}+\mathrm{0,30}+\mathrm{0,40}}=\frac{\mathrm{72,50}}{\mathrm{1,00}}=\mathrm{72,50}$

Siga em Frente...

A moda é o valor que aparece com maior frequência no conjunto de dados e é denominado valor modal. Um conjunto de dados pode ter mais de uma moda (multimodal) ou nenhuma moda (amodal). Para ilustrar o cálculo da moda, consideraremos os dados do exemplo 1, que constam na Tabela 2. A moda é o valor que mais se repete, logo a temperatura modal é 13,5 °C, pois essa aparece 4 vezes no conjunto de dados.

Por sua vez, a mediana é o valor que divide o conjunto de dados em duas partes iguais, ou seja, é o valor tal que se encontra no centro do conjunto de dados. É importante lembrar que, para determinar a mediana, é necessário que o conjunto de dados esteja ordenado. Se esse conjunto tem um número ímpar de dados, a mediana é o valor central; porém, se o conjunto tem um número par de dados, a mediana é a média dos dois valores centrais.

Considerando os dados do exemplo 1, vamos determinar a mediana desses dados. Para encontrarmos a mediana, é necessário primeiro que ordenemos o conjunto de dados:

13,5

13,5

13,5

13,5

14

15,5

16

18

18

18,5

19,5

20

20

20

21

21,5

Tabela 3 | Conjunto de dados. Fonte: elaborada pela autora.

 

Após ordenar os dados, temos que identificar o valor os dois valores que se encontram no meio, visto que há um número par de dados. Assim, a temperatura mediana será a média aritmética dos valores que se encontram na oitava e na nona posição, isto é $\frac{18+18}{2}=18 °C$.

Quando se trata de um conjunto de dados unimodal, ou seja, com apenas uma moda, podemos utilizar as medidas de tendência central para analisar se a distribuição de dados é assimétrica ou simétrica. Uma distribuição é simétrica se o valor da média é igual ao da moda e igual ao da mediana; caso contrário, essa distribuição é assimétrica. Se a média é maior que a mediana, e a mediana é maior que a moda, temos uma distribuição assimétrica positiva. Se a média é menor que a mediana, e a mediana é menor que a moda, temos uma distribuição assimétrica negativa, conforme ilustrado na Figura 1.

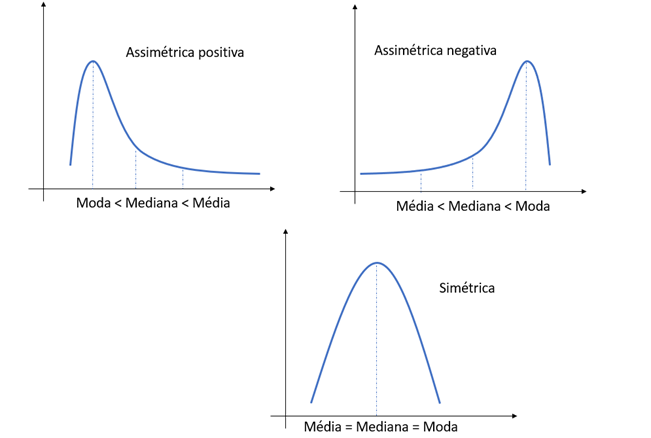
A correta determinação dessas medidas de tendência central ajuda o pesquisador a compreender os dados de modo mais preciso. Com conhecimento da média, da mediana e da moda dos dados, é possível embasar as decisões em informações concisas e pertinentes.

Vamos Exercitar?

Vamos retornar à nossa situação inicial e calcular as medidas de tendência central referentes às alturas da turma. O primeiro passo é organizar os dados da Tabela 1 em ordem crescente (Tabela 3).

155	155	156	164	165	165	165	165	166	167
167	168	169	170	175	176	178	178	180	190

Tabela 3 | Dados ordenados referentes à altura (cm). Fonte: elaborado pela autora.

 

A média aritmética será dada pelo quociente entre a soma de todos os valores e a quantidade total de dados:

$\stackrel{-}{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$

$\stackrel{-}{x}=\frac{1}{20}\left(155+155+156+164+165+165+165+165+166+167+167+168+169+170+175+176+178+178+180+190\right)$

$\stackrel{-}{x}=\frac{1}{20}\left(3374\right)=\mathrm{168,7}$

Logo, a altura média é 168,7 centímetros.

Agora, temos que determinar a mediana dos dados. Como há um número par de dados, a mediana é a média aritmética dos dois dados que dividem o conjunto de dados em duas partes de mesmo tamanho, isto é, a média aritmética entre os valores que se encontram nas posições 10 e 11:

$\frac{167+167}{2}=167$

Portanto, a mediana é 167 centímetros.

A moda é o dado que mais aparece no conjunto de dados; nesse caso, a moda é 165 centímetros, visto que esse dado aparece 4 vezes no conjunto dos dados.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre as medidas de tendência central, recomendamos que você leia o capítulo 3 do livro Estatística. Ao final do capítulo, selecione alguns exercícios e os resolva!
 

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023. 

Medidas de dispersão

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Já estudamos as medidas de tendência central, que nem sempre conseguem fornecer uma imagem completa de conjuntos de dados. Por exemplo, suponha que tenhamos três conjuntos de dados, todos com uma média de 10. A questão é: essa média é representativa para todos esses conjuntos de dados? Quando podemos considerar uma média como representativa em um conjunto de dados? Além disso, quais ferramentas podem ser empregadas para complementar as medidas de tendência central na descrição de um conjunto de dados?

Para auxiliar as medidas de tendência central na descrição de um conjunto, utilizamos também as medidas de dispersão, voltadas a analisar a variabilidade dos dados no entorno da média aritmética. Veremos mais detalhes sobre a amplitude, a variância, o desvio-padrão, o desvio médio e o coeficiente de variação.

Com o intuito de ilustrar como esses conceitos podem ser aplicados, considere que uma pesquisa foi realizada para analisar o salário anual de professores de escolas públicas e privadas. A Tabela 1 apresenta uma amostra desses salários.

Escolas privadas	$R\$ 38.600$	$R\$ 38.100$	$R\$ 38.700$	$R\$ 36.800$	$R\$ 34.800$	$R\$ 35.900$	$R\$ 39.900$	$R\$ 36.200$
Escolas públicas	$R\$ 21.800$	$R\$ 18.400$	$R\$ 20.300$	$R\$ 17.600$	$R\$ 19.700$	$R\$ 18.300$	$R\$ 19.400$	$R\$ 20.800$

Tabela 1 | Salários anuais dos professores. Fonte: elaborada pela autora.

 

Com base nesses dados, verifique a amplitude de cada uma das amostras e qual amostra de salário é mais homogênea.

Para determinarmos a amostra de salário mais homogênea, precisamos encontrar o desvio-padrão e a média aritmética.

Bons estudos!

Vamos Começar!

Você já estudou as medidas de tendência central: média aritmética, moda e mediana. Mas será que essas medidas apenas são suficientes para caracterizar um conjunto de dados? Para respondermos a essa pergunta, vamos analisar os seguintes conjuntos de dados:

Conjunto 1	1	2		5			9		10			11			15			17			20
Conjunto 2	5	5			5			7		10			10			10			10			13			13		15		17
Conjunto 3	10		10			10					10			10			10			10			10			10		10

Tabela 2 | Conjunto de dados. Fonte: elaborada pela autora.

 

Observe que esses três conjuntos de dados têm média aritmética 10, porém apresentam características diferentes no que se refere à variabilidade dos dados. No conjunto 3, não existe variabilidade dos dados, visto que ele é formado apenas pelo valor 10. No conjunto 1, há muitos elementos diferentes da média 10 e, no conjunto 2, a média 10 representa bem o conjunto de dados, mas existem elementos levemente diferenciados. Assim, podemos concluir que a média 10 representa otimamente o conjunto de dados 3, representa bem o conjunto de dados 2, porém não representa bem o conjunto de dados 1. Nesse sentido, faz-se necessário conhecermos medidas que avaliem a representatividade da média.

Para tal, estudaremos as medidas de dispersão, que analisam a variabilidade dos dados no entorno da média. Retomando nosso exemplo inicial, perceba que no conjunto 1 os dados estão dispersos em relação à média. Já no conjunto 2, os dados se encontram nas proximidades da média e, no conjunto 3, não há dados dispersos. Logo, temos conjuntos de dados com mesma média, mas com variabilidade diferentes.

As principais medidas de dispersão são a amplitude total, a variância, o desvio-padrão e o coeficiente de variação.

A amplitude, $A_t$, de um conjunto de dados é dada pela diferença entre o maior e o menor valor desse conjunto. Observe que a amplitude utiliza somente dois dados do conjunto, o que a torna uma medida não tão fidedigna para analisar a variabilidade dos dados.

Ao contrário da amplitude, as demais medidas de dispersão utilizam todos os dados do conjunto. Dentre essas medidas, temos o desvio médio e o desvio-padrão. Segundo Silva et al. (2018, p. 68), “o conceito estatístico de desvio corresponde ao conceito matemático de distância”. Podemos analisar a dispersão dos dados no entorno da média por meio dos desvios de cada elemento do conjunto de dados em relação à média desse conjunto. O desvio médio, , é definido como uma média aritmética dos desvios de cada elemento do conjunto de dados. O desvio médio é dado por:

$DMS=\frac{{\sum }_{i=0}^n\left|x_i-\stackrel{-}{x}\right|}{n}$

em que, $\stackrel{-}{x}$ é a média do conjunto de dados e  é a quantidade total de dados.

Note que o desvio médio é influenciado por todos os elementos do conjunto de dados, o que o torna uma medida estatística altamente sensível, uma vez que a alteração de um único valor no conjunto de dados resulta em uma mudança no desvio médio. Apesar disso, uma das desvantagens de trabalhar com o desvio médio é a necessidade de lidar com valores absolutos, visto que a diferença $x_i-\stackrel{-}{x}$ é interpretada como uma distância. Outra forma de garantirmos uma valor positivo para essa diferença é se elevarmos a diferença ao quadrado, isto é, ${\left(x_i-\stackrel{-}{x}\right)}^2$. Ao substituirmos $\left|x_i-\stackrel{-}{x}\right|$ por ${\left(x_i-\stackrel{-}{x}\right)}^2$ na fórmula do desvio médio, chegamos a uma nova medida de dispersão: a variância amostral, ou a variância populacional.

Siga em Frente...

A variância é uma média aritmética calculada com base nos quadrados dos desvios obtidos entre os elementos do conjunto e sua média. Ao calcular a variância, é crucial considerar se o conjunto de dados representa uma amostra ou uma população, uma vez que isso tem impacto direto no procedimento de cálculo. A variância populacional é denotada por ${\sigma }^2$ e dada por:

${\sigma }^2=\frac{{\sum }_{i=0}^n{\left(x_i-\mu \right)}^2}{n}$

Já a variância amostral é denotada por  e é dada por:

$S^2=\frac{{\sum }_{i=0}^n{\left(x_i-\stackrel{-}{x}\right)}^2}{n-1}$

Quando calculamos a variância, elevamos ao quadrado a diferença $x_i-\stackrel{-}{x}$, o que acarreta a elevação ao quadrado da unidade de medidas dos elementos que compõem o conjunto de dados. Logo, o valor da variância não pode ser interpretado, pois ele não pode ser comparado diretamente com os elementos do conjunto de dados. Para suprir essa deficiência, calcula-se o desvio-padrão, que tem a mesma unidade de medida dos elementos do conjunto de dados, uma vez que é obtido por meio da raiz quadrada da variância. Trata-se de uma das medidas de dispersão mais importantes, pois permite interpretar o conjunto de dados. O desvio-padrão é a raiz quadrada da variância, então o desvio-padrão populacional é dado por:

$\sigma =\sqrt{{\sigma }^2}=\sqrt{\frac{{\sum }_{i=0}^n{\left(x_i-\mu \right)}^2}{n}}$

E o desvio amostral é dado por:

$S=\sqrt{S^2}=\sqrt{\frac{{\sum }_{i=0}^n{\left(x_i-\stackrel{-}{x}\right)}^2}{n-1}}$

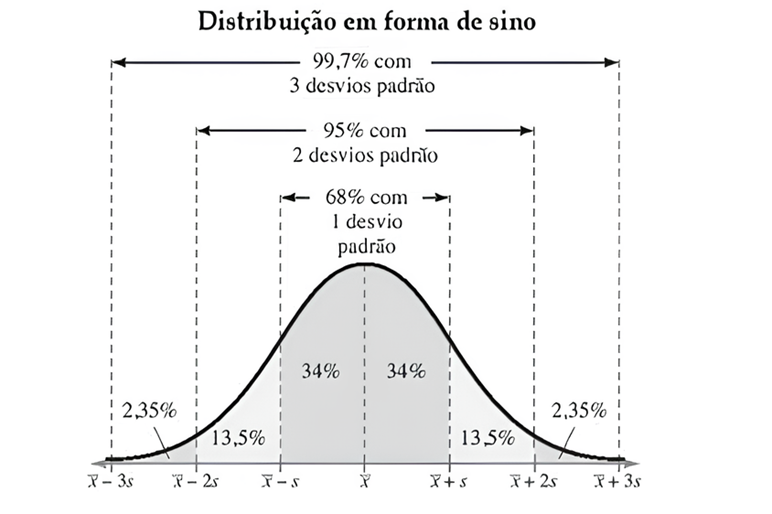
Podemos dizer que quanto maior o desvio-padrão, maior a dispersão dos dados. Segundo Larson e Farber (2015), a regra empírica nos mostra a importância do desvio-padrão, visto que com ele podemos analisar distribuições aproximadamente simétricas e com curva em forma de sino. No caso de distribuições simétricas com formato de curva de sino, o desvio-padrão apresenta as seguintes características:

• Em torno de  dos dados estão dentro de um desvio-padrão em relação à média.
• Em torno de  dos dados estão dentro de dois desvios-padrão em relação à média.
• Em torno de  dos dados estão dentro de três desvios-padrão em relação à média.

A Figura 1 ilustra as características citadas anteriormente.

Outra medida de dispersão é o coeficiente de variação, que pode ser interpretado como a variabilidade dos dados em relação à média e permite expressar a variabilidade dos dados sem a influência da ordem de grandeza da variável. O coeficiente de variação, $CV$, é dado por

$CV=\frac{S}{\stackrel{-}{x}}\cdot 100$

No caso de lidarmos com uma população, ele será dado por:

$CV=\frac{\sigma }{\mu }\cdot 100$

O coeficiente de variação é considerado uma medida de dispersão relativa, pois permite que se compare a dispersão de diferentes distribuições, como diferentes médias e desvio-padrão. Quanto menor for o valor do coeficiente de variação, mais homogêneo é o conjunto de dados, isto é, os dados estão mais concentrados em torno da média. Podemos dizer que se o coeficiente de variação for menor que $15\%$, o conjunto de dados tem baixa dispersão; se o coeficiente estiver entre $15\%$ e $30\%$, o conjunto de dados tem média dispersão; e se o coeficiente for maior que $30\%$, o conjunto de dados tem alta dispersão.

As medidas estudadas nesta aula têm aplicações específicas e são úteis em diferentes situações, ajudando a complementar as medidas de tendência central na análise estatística completa de um conjunto de dados. Em resumo, as medidas de dispersão desempenham um papel fundamental na descrição e na interpretação de dados estatísticos. 

Vamos Exercitar?

Vamos retornar à nossa situação inicial, calcular a amplitude de cada amostra da Tabela 1 (Tabela 3) e analisar qual delas é mais homogênea.

Escolas privadas	$R\$ 38.600$	$R\$ 38.100$	$R\$ 38.700$	$R\$ 36.800$	$R\$ 34.800$	$R\$ 35.900$	$R\$ 39.900$	$R\$ 36.200$
Escolas públicas	$R\$ 21.800$	$R\$ 18.400$	$R\$ 20.300$	$R\$ 17.600$	$R\$ 19.700$	$R\$ 18.300$	$R\$ 19.400$	$R\$ 20.800$

Tabela 3 – Salários anuais dos professores. Fonte: elaborada pela autora.

 

Denominaremos a amostra das escolas privadas AM1 e a das escolas públicas, AM2. A amplitude total de cada amostra será dada pela diferença entre o menor e o maior valor. Assim teremos:

$A_{AM1}=39900-34800=5100$

$A_{AM2}=21800-17600=4200$

A fim de determinarmos qual amostra de dados é mais homogênea, temos que calcular o coeficiente de variação. Para tal, será necessário calcular o desvio-padrão amostral e a média amostral.

Passo 1: calcular a média aritmética de cada amostra.

$\stackrel{ }{\overline{)x_{AM1}}}=\frac{\sum x_i}{n}=\frac{38600+38100+38700+36800+34800+35900+39900+36200}{8}$

$\frac{ }{x_{AM1}}=\frac{299000}{8}=37375$

$\stackrel{ }{\overline{)x_{AM2}}}=\frac{\sum x_i}{n}=\frac{21800+18400+20300+17600+19700+18300+19400+20800}{8}$

$\stackrel{ }{\overline{)x_{AM2}}}=\frac{156300}{8}=\mathrm{19537,50}$

 

Passo 2 e 3: encontrar o quadrado dos desvios.

Para a amostra 1, temos:

AM1	$x_i-\stackrel{ }{\overline{)x_{AM1}}}$	${\left(x_i-\stackrel{ }{\overline{)x_{AM1}}}\right)}^2$
R$ 38.600,00	R$ 1.225,00	1500625
R$ 38.100,00	R$ 725,00	525625
R$ 38.700,00	R$ 1.325,00	1755625
R$ 36.800,00	-R$ 575,00	330625
R$ 34.800,00	-R$ 2.575,00	6630625
R$ 35.900,00	-R$ 1.475,00	2175625
R$ 39.900,00	R$ 2.525,00	6375625
R$ 36.200,00	-R$ 1.175,00	1380625

Tabela 4 | Amostra 1. Fonte: elaborada pela autora.

 

Para a amostra 2, temos:

AM2	$x_i-\stackrel{ }{\overline{)x_{AM2}}}$	${\left(x_i-\stackrel{ }{\overline{)x_{AM2}}}\right)}^2$
R$ 21.800,00	R$ 2.262,50	5118906
R$ 18.400,00	-R$ 1.137,50	1293906
R$ 20.300,00	R$ 762,50	581406,3
R$ 17.600,00	-R$ 1.937,50	3753906
R$ 19.700,00	R$ 162,50	26406,25
R$ 18.300,00	-R$ 1.237,50	1531406
R$ 19.400,00	-R$ 137,50	18906,25
R$ 20.800,00	R$ 1.262,50	1593906

 

 

 

 

 

 

 

 

 

 

 

Tabela 5 | Amostra 2. Fonte: elaborada pela autora.

 

Passo 4: determinar o somatório dos quadrados dos desvios.

Para a amostra 1, temos:

$\sum {\left(x_i-\stackrel{ }{\overline{)x_{AM1}}}\right)}^2=1500625+525625+1755625+330625+6630625+2175625+6375625+1380625=20675000$

Para a amostra 2, temos:

$\sum {\left(x_i-\stackrel{ }{\overline{)x_{AM2}}}\right)}^2=5118906+1293906+\mathrm{581406,3}+3753906+\mathrm{26406,25}+1531406+\mathrm{18906,25}+1593906=13918750$

Passo 5: determinar a variância amostral.

$S_{AM1}^2=\frac{\sum {\left(x_i-\stackrel{ }{\overline{)x_{AM1}}}\right)}^2}{8-1}=\frac{20675000}{7}=\mathrm{2953571,43}$

$S_{AM2}^2=\frac{\sum {\left(x_i-\stackrel{ }{\overline{)x_{AM2}}}\right)}^2}{8-1}=\frac{13918550}{7}=\mathrm{1988392,86}$

Passo 6: determinar o desvio padrão amostral.

$S_{AM1}=\sqrt{S_{AM1}^2}=\sqrt{\mathrm{2953571,43}}=\mathrm{1718,60}$

$S_{AM2}=\sqrt{S_{AM2}^2}=\sqrt{\mathrm{1988392,86}}=\mathrm{1410,10}$

Agora temos que encontrar o coeficiente de variação de cada amostra.

$C{V}_{AM1}=\frac{S_{AM1}}{\stackrel{ }{\overline{)x_{AM1}}}}\cdot 100=\frac{\mathrm{1718,60}}{37375}\cdot 100=\mathrm{4,60}\%$

$C{V}_{AM2}=\frac{S_{AM2}}{\stackrel{ }{\overline{)x_{AM2}}}}\cdot 100=\frac{\mathrm{1410,1}}{\mathrm{19537,50}}\cdot 100=\mathrm{7,22}\%$

Observe que as duas amostras reúnem dados homogêneos, uma vez que os coeficientes de variação são menores do que $15\%$. Ao compararmos os coeficientes de variação, podemos dizer que os salários dos professores das escolas privadas são mais homogêneos do que os dos professores das escolas públicas, visto que $C{V}_{AM1}<C{V}_{AM2}$.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre as medidas de dispersão, recomendamos que você leia o capítulo 5 do livro Estatística. Ao final do capítulo, selecione alguns exercícios e os resolva!

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

Estatística descritiva

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Chegada

Olá, estudante!

Para desenvolver a competência desta unidade, que é compreender os princípios básicos da estatística descritiva a fim de empregá-los na análise e na intepretação de problemas que envolvam pesquisas estatísticas, você deve primeiramente reconhecer quais são esses princípios.

É essencial identificar a que grupo de dados se refere uma pesquisa, assim como quais informações e características estão sendo analisadas. É importante lembrar que, para considerar algo como uma população, é necessário que os dados compartilhem pelo menos uma característica em comum. Uma amostra, por sua vez, é uma parte representativa dessa população.

As variáveis representam as diferentes características dos dados e podem ser quantitativas ou qualitativas. As variáveis qualitativas não podem ser medidas numericamente e podem ser ordinais, quando é possível estabelecer uma ordem entre elas, ou nominais, quando essa ordem não é aplicável. Por outro lado, as variáveis quantitativas são aquelas que podem ser medidas numericamente e podem ser discretas, quando seus valores possíveis são finitos ou contáveis, ou contínuas, quando os valores possíveis pertencem a um intervalo de números reais.

Outro elemento fundamental na abordagem de problemas estatísticos diz respeito à organização dos dados de uma pesquisa, a qual pode ser realizada mediante a criação de tabelas e gráficos. Quando se pretende construir uma tabela de frequência, o primeiro passo consiste em avaliar se os dados serão organizados em classes ou não. Em seguida, é preciso calcular as frequências absoluta, relativa e acumulada. A frequência absoluta representa o número de vezes que um dado específico ocorre, enquanto a frequência relativa corresponde à proporção entre a frequência absoluta e o total de dados, geralmente expressa em forma de porcentagem. Já a frequência acumulada quantifica os valores até determinado ponto, não se limitando a um valor único. Quando se opta por uma tabela de frequência com classes, é necessário estabelecer o número de classes e, em seguida, definir a amplitude de cada classe.

A organização dos dados facilita a interpretação deles; e, para aprimorar essa interpretação, dispomos de medidas de tendência central e medidas de dispersão. As medidas de tendência central incluem a média aritmética, a moda e a mediana. A média aritmética é obtida ao dividir a soma de todos os dados pela quantidade total de dados. Já a moda representa o elemento com a maior frequência no conjunto de dados — lembrando que um conjunto pode não ter moda ou apresentar mais de uma moda. E a mediana é o valor que divide igualmente o conjunto de dados ordenados em duas partes.

As medidas de dispersão estão diretamente ligadas à variação dos dados. A amplitude corresponde à diferença entre o valor máximo e o valor mínimo do conjunto. Para calcular a variância e o desvio-padrão, é preciso determinar se os dados pertencem a uma amostra ou a uma população. Já o coeficiente de variação é uma medida que fornece uma interpretação da variação dos dados em relação à média.

Compreender esses conceitos é essencial para a análise e a interpretação de problemas que envolvem pesquisas estatísticas.

É Hora de Praticar!

A estatística desempenha um papel crucial em nossa compreensão do mundo, auxiliando na coleta, na organização e na interpretação de dados para embasar decisões e descobertas em uma ampla gama de campos. Trata-se de uma ferramenta poderosa para lidar com a incerteza e extrair conhecimento significativo de informações complexas. Vamos examinar uma situação para demonstrar como os conceitos vistos nesta unidade podem ser aplicados.

Consideremos que você faça parte de uma startup especializada na elaboração de relatórios estatísticos. Um de seus clientes é um pesquisador que conduziu um experimento para avaliar o impacto de um composto químico no crescimento de plantas de tamanho médio. O pesquisador forneceu duas amostras, cada uma contendo 30 medições da altura das plantas. Ambas as amostras são formadas por plantas cultivadas simultaneamente; a única diferença entre elas é o fato de que um grupo recebeu regularmente o composto químico, enquanto o outro grupo não o recebeu. A primeira amostra compreende as medições de altura das plantas não expostas ao composto químico, enquanto a segunda amostra compreende as medições de altura das plantas submetidas regularmente ao referido composto. A Tabela 1 apresenta os valores da primeira amostra.

120	120	125	126	129
130	135	145	145	150
150	150	155	158	159
160	170	189	200	201
210	210	215	218	219
230	235	240	250	270

Tabela 1 | Valores da amostra 1 (cm). Fonte: elaborada pela autora.

 

A Tabela 2 apresenta os valores da segunda amostra.

125	130	131	132	132
135	138	138	146	155
155	160	165	168	169
170	175	180	195	210
215	215	220	225	230
235	240	245	255	260

Tabela 2 | Valores da amostra 2 (cm). Fonte: elaborado pela autora.

 

Seu trabalho é elaborar um relatório preliminar sobre esses dados. É importante que você apresente os dados de forma organizada e forneça medidas estatísticas a fim de embasar alguns resultados iniciais sobre o experimento. Pensando nisso, você decidiu que seu relatório deveria conter:

• Tabelas de distribuição de frequência com classe das duas amostras.
• Histogramas das tabelas de distribuição de frequência.
• Medidas de tendência central das amostras sem agrupar os dados.
• Medidas de dispersão das amostras sem agrupar os dados.
• Determinação de qual amostra apresenta a maior variabilidade dos dados.

A elaboração desse relatório demandará a utilização de diferentes conceitos estatísticos; então, antes de começar, reflita sobre quais conceitos você utilizará.

Reflita

Considerando a ampla variedade de situações em que os conceitos abordados nesta unidade podem ser aplicados, convidamos você a refletir sobre duas questões:

1. De que maneira a estatística descritiva pode ser benéfica para solucionar desafios em seu campo de atuação?
2. De que forma a análise e a interpretação de dados provenientes de pesquisas estatísticas podem contribuir para o processo de tomada de decisão?

Resolução do estudo de caso

Vamos iniciar a elaboração do relatório construindo a tabela de distribuição de frequência com classe, o histograma e as medidas de tendência central e as medidas de dispersão para cada uma das amostras.

 

Amostra 1

Para a construção da tabela de distribuição de frequência, precisamos encontrar a quantidade de classes, a amplitude de cada intervalo de classe, os limites inferiores e superiores de cada intervalo e, por fim, as frequências absoluta, relativa e acumulada.

Ambas as tabelas terão 6 classes, visto que $\sqrt{30}\cong \mathrm{5,5}$. Considerando esse número de classes e que a amplitude total da amostra 1 é $270-120=150$, a amplitude de cada classe para a amostra 1 será $h=\frac{150}{6}=25$. A Tabela 3 mostra a distribuição de frequência para a amostra 1.

Altura	Frequência absoluta ${\mathit{f}}_{\mathit{a}}$	Frequência relativa ${\mathit{f}}_{\mathit{r}}$	Frequência acumulada ${\mathit{f}}_{\mathit{a}\mathit{c}}$
$120⊢145$	7	$\mathrm{23,3}\%$	$\mathrm{23,3}\%$
$145⊢170$	9	$30\%$	$\mathrm{53,3}\%$
$170⊢195$	2	$\mathrm{6,7}\%$	$60\%$
$195⊢220$	7	$\mathrm{23,3}\%$	$\mathrm{83,3}\%$
$220⊢245$	3	$10\%$	$\mathrm{93,3}\%$
$245-270$	2	$\mathrm{6,7}\%$	$100\%$

Tabela 3 | Tabela de frequência para a amostra 1. Fonte: elaborada pela autora.

 

A Figura 1 mostra o histograma para a amostra 1.

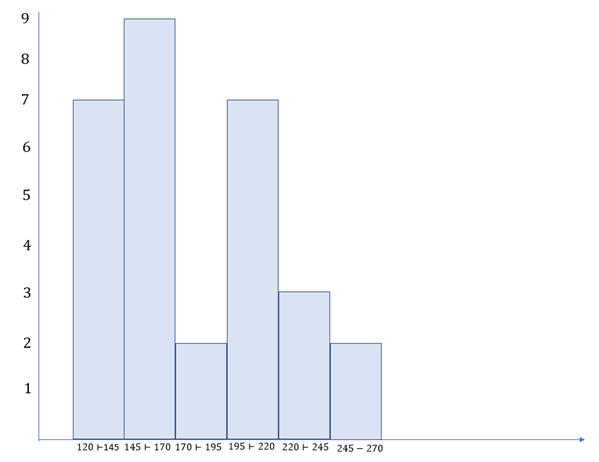
Agora, é necessário calcular as medidas de tendência central. A média aritmética será determinada pela divisão da soma das alturas, de acordo com a Tabela 1, pela quantidade total de dados, que, nesse caso, corresponde a 30. Logo, a média será:

$\stackrel{-}{x_1}=\frac{\sum x_i}{n}=\frac{5314}{30}=\mathrm{177,14}$

A moda da amostra 1 é a altura de 150 centímetros, visto que essa altura aparece 3 vezes no conjunto de dados. Como temos uma quantidade par de dados, a mediana será a média aritmética entre os valores que ocupam as posições 15 e 16:

$m_d=\frac{159+160}{2}=\frac{319}{2}=\mathrm{159,5}$

Falta calcularmos as medidas de dispersão. Para isso, precisamos do quadrado dos desvios (Tabela 4).

Altura
120	-57,13	3264,22
120	-57,13	3264,22
125	-52,13	2717,88
126	-51,13	2614,62
129	-48,13	2316,82
130	-47,13	2221,55
135	-42,13	1775,22
145	-32,13	1032,55
145	-32,13	1032,55
150	-27,13	736,22
150	-27,13	736,22
150	-27,13	736,22
155	-22,13	489,88
158	-19,13	366,08
159	-18,13	328,82
160	-17,13	293,55
170	-7,13	50,88
189	11,87	140,82
200	22,87	522,88
201	23,87	569,62
210	32,87	1080,22
210	32,87	1080,22
215	37,87	1433,88
218	40,87	1670,08
219	41,87	1752,82
230	52,87	2794,88
235	57,87	3348,55
240	62,87	3952,22
250	72,87	5309,55
270	92,87	8624,22

Tabela 4 | Quadrado dos desvios da amostra 1. Fonte: elaborada pela autora.

 

A variância amostral será dada por:

$S_1^2=\frac{\sum {\left(x_i-\stackrel{-}{x_1}\right)}^2}{30-1}=\frac{\mathrm{562257,47}}{29}=\mathrm{1939,91}$

O desvio-padrão amostral será:

$S_1=\sqrt{S_1^2}=\sqrt{\mathrm{1939,91}}=\mathrm{44,04}$

O coeficiente de variação será:

$C{V}_1=\frac{S_1}{\stackrel{-}{x_1}}\cdot 100=\frac{\mathrm{44,04}}{177.14}\cdot 100=\mathrm{37,60}\%$

Amostra 2

A tabela de distribuição de frequência da amostra 2 tem 6 classes, e sua amplitude total é $260-125=135$. A amplitude de cada classe para a amostra 1 será $h=\frac{135}{6}=\mathrm{22,5}$. Assim, a Tabela 5 mostra a distribuição de frequência para a amostra 2.

Altura	Frequência absoluta ${\mathit{f}}_{\mathit{a}}$	Frequência relativa ${\mathit{f}}_{\mathit{r}}$	Frequência acumulada ${\mathit{f}}_{\mathit{a}\mathit{c}}$
$125⊢\mathrm{147,5}$	9	$30\%$	$30\%$
$\mathrm{147,5}⊢170$	6	$20\%$	$50\%$
$170⊢\mathrm{192,5}$	3	$10\%$	$60\%$
$\mathrm{192,5}⊢215$	2	$\mathrm{6,7}\%$	$\mathrm{66,7}\%$
$215⊢\mathrm{237,5}$	6	$20\%$	$\mathrm{86,7}\%$
$\mathrm{237,5}-260$	4	$\mathrm{13,3}\%$	$100\%$

Tabela 5 | Tabela de frequência para a amostra 2. Fonte: elaborada pela autora.

 

 

A Figura 2 mostra o histograma para a amostra 2.

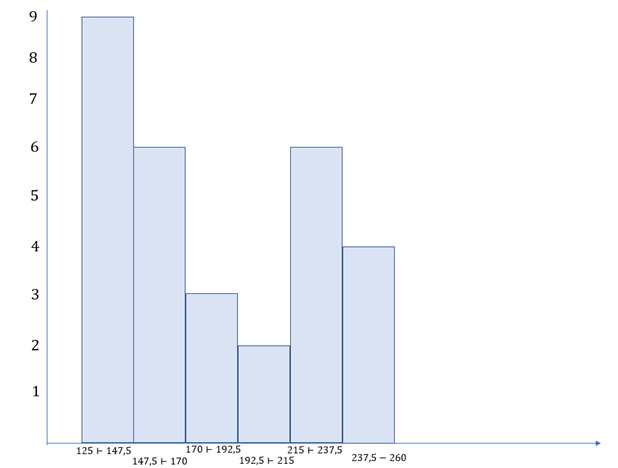
Agora, é necessário calcular as medidas de tendência central. A média aritmética será determinada pela divisão da soma das alturas, de acordo com a Tabela 2, pela quantidade total de dados, que, nesse caso, corresponde a 30. Logo, a média será:

$\stackrel{-}{x_2}=\frac{\sum x_i}{n}=\frac{5449}{30}=\mathrm{181,63}$

A amostra 2 tem mais de uma moda, visto que os valores aparecem duas vezes no conjunto de dados. As modas são 132 centímetros, 138 centímetros, 155 centímetros e 215 centímetros. Como temos uma quantidade par de dados, a mediana será a média aritmética entre os valores que ocupam as posições 15 e 16:

$m_d=\frac{169+170}{2}=\frac{339}{2}=\mathrm{169,5}$

Falta calcularmos as medidas de dispersão. Para isso, precisamos do quadrado dos desvios (Tabela 6).

Altura
125	-56,63	3207,33
130	-51,63	2666,00
131	-50,63	2563,73
132	-49,63	2463,47
132	-49,63	2463,47
135	-46,63	2174,67
138	-43,63	1903,87
138	-43,63	1903,87
146	-35,63	1269,73
155	-26,63	709,33
155	-26,63	709,33
160	-21,63	468,00
165	-16,63	276,67
168	-13,63	185,87
169	-12,63	159,60
170	-11,63	135,33
175	-6,63	44,00
180	-1,63	2,67
195	13,37	178,67
210	28,37	804,67
215	33,37	1113,33
215	33,37	1113,33
220	38,37	1472,00
225	43,37	1880,67
230	48,37	2339,33
235	53,37	2848,00
240	58,37	3406,67
245	63,37	4015,33
255	73,37	5382,67
260	78,37	6141,33

Tabela 6 | Quadrado dos desvios da amostra 2. Fonte: elaborada pela autora.

 

A variância amostral será dada por:

$S_2^2=\frac{\sum {\left(x_i-\stackrel{-}{x_2}\right)}^2}{30-1}=\frac{\mathrm{54002,97}}{29}=\mathrm{1862,17}$

O desvio-padrão amostral será:

$S_2=\sqrt{S_2^2}=\sqrt{\mathrm{1862,17}}=\mathrm{43,15}$

O coeficiente de variação será:

$C{V}_2=\frac{S_2}{\stackrel{-}{x_2}}\cdot 100=\frac{\mathrm{43,15}}{\mathrm{181,63}}\cdot 100=\mathrm{23,76}\%$

Comparando os coeficientes de variação, temos que os dados da amostra 1 são mais dispersos que os da amostra 2, visto que, $C{V}_1>C{V}_2$; ou seja, os dados da amostra 2 são mais homogêneos do que os da amostra 1.

Com base na análise das médias das duas amostras, podemos dizer que as plantas cultivadas com o componente químico apresentam uma altura média maior do que as plantas que não receberam esse componente.

Dê o play!

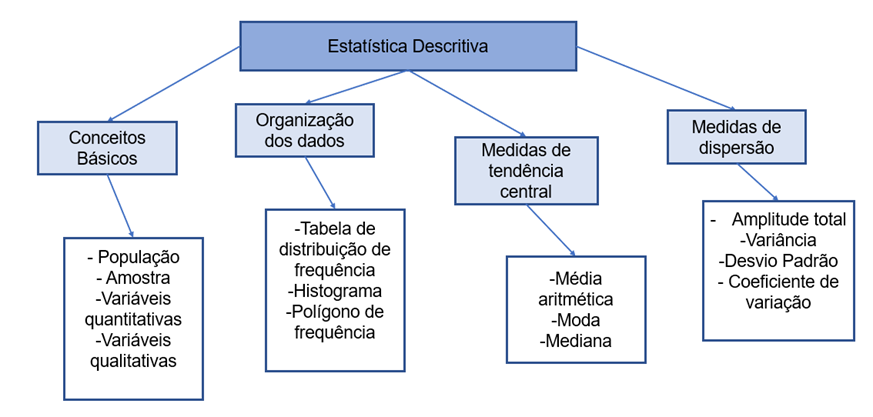
Assimile

Ao explorar o campo da estatística descritiva, é essencial que você tenha um domínio dos principais conceitos envolvidos. A Figura 3 ilustra quais são esses conceitos.

Referências

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.