Probabilidade

Introdução à probabilidade

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Qual é a probabilidade de ser atingido por um raio em comparação com a de ganhar na Mega Sena? Embora possa soar como uma piada, a realidade é que o primeiro evento é mais provável do que o segundo. As chances de acertar as seis dezenas na Mega Sena são aproximadamente uma em 50 milhões, enquanto as chances de ser atingido por um raio ao longo da vida são uma em 1 milhão, de acordo com o Grupo de Eletricidade Atmosférica (ELAT).

A chance de ocorrência de determinado evento é mensurada pela probabilidade. Trata-se de uma área fundamental da matemática e da estatística que se concentra em quantificar e entender a incerteza em situações que envolvem aleatoriedade. A teoria da probabilidade é amplamente usada em diversas áreas, como estatística, ciências naturais, engenharia, economia, jogos de azar, previsão do tempo e muito mais, para tomar decisões informadas em face de incertezas. Ela fornece uma estrutura matemática para lidar com a aleatoriedade e é essencial para a modelagem e a análise de eventos e processos estocásticos.

Nesta aula, estudaremos as noções básicas que envolvem a probabilidade. A fim de entender como podemos aplicar esse conceito, suponha uma empresa de peças automobilística esteja realizando um teste de qualidade; para isso, selecionou um lote formado por 100 peças boas, 8 com defeitos e 3 com defeitos graves. Sabendo que uma peça é escolhida aleatoriamente, indique a probabilidade de que:

1. Ela não tenha defeitos graves.
2. Ela não tenha defeitos.
3. Ela seja boa ou tenha defeitos graves.

Se retirarmos duas peças ao acaso, indique a probabilidade de que:

1. Ambas sejam perfeitas.
2. Pelo menos uma seja perfeita.
3. Nenhuma tenha defeito grave.
4. Nenhuma seja perfeita.

Para estabelecer essas probabilidades, é necessário examinar como calcular a probabilidade da ocorrência de um evento específico.

Bons estudos!

Vamos Começar!

O estudo da probabilidade como ramo da matemática tem raízes que remontam a mais de três séculos, e sua origem está ligada a problemas relacionados a jogos de azar. O conceito de probabilidade diz respeito à análise da aleatoriedade e da incerteza. Sempre que estamos diante de uma situação que envolve múltiplos desfechos, a teoria de probabilidade fornece ferramentas para quantificar as probabilidades ou as possibilidades ligadas a esses diferentes desfechos (Devore, 2018).

Por exemplo, ao jogar um dado não viciado, a probabilidade de cair a face com o número 2 é de aproximadamente 0,17%. Como podemos determinar esse valor? Antes precisamos entender alguns conceitos. A ação de jogar o dado é denominada experimento. Segundo Larson e Farber (2015, p. 125, grifo nosso), “um experimento probabilístico é uma ação, ou tentativa sujeita à lei do acaso, pela qual resultados específicos (contagens, medições ou respostas) são obtidos”.

Ao lançar um dado não viciado, as opções para as faces que ficarão voltadas para cima são: a face com o número 1, a face com o número 2, a face com o número 3, a face com o número 4, a face com o número 5 e a face com o número 6. Em outras palavras, ao lançar um dado, temos 6 possibilidades de faces voltadas para cima. A todas essas possibilidades damos o nome de espaço amostral, descrito por Larson e Farber (2015, p. 125) como “o conjunto de todos os resultados possíveis de um experimento probabilístico”. Geralmente denotamos o espaço amostral pela letra grega $\mathbf{\Omega }$.

Quando expressamos o desejo de calcular a probabilidade de que a face com o número 2 seja a que apareça, estamos examinando uma das seis possibilidades existentes no espaço amostral. Nesse contexto, consideramos que a ocorrência da face com o número 2 constitui um evento. “Um evento é um subconjunto do espaço amostral. Ele pode consistir em um ou mais resultados” (Larson; Farber, 2015, p. 125, grifo nosso).

A abordagem empregada para calcular uma probabilidade está relacionada ao tipo específico de probabilidade em questão. Existem três categorias principais: probabilidade clássica, probabilidade empírica e probabilidade subjetiva. A probabilidade de um evento A é representada como P(A) e pronunciada como “probabilidade do evento A” (Larson; Farber, 2015). Vamos direcionar nossa atenção para a probabilidade clássica, também conhecida como probabilidade teórica, aplicada quando todos os resultados em um espaço amostral têm a mesma probabilidade de ocorrência. A probabilidade clássica para um evento A é dada por:

$P\left(A\right)=\frac{\mathrm{número}\mathrm{ }\mathrm{de}\mathrm{ }\mathrm{resultado}\mathrm{ }\mathrm{do}\mathrm{ }\mathrm{evento}\mathrm{ }\mathrm{A}}{\mathrm{número}\mathrm{ }\mathrm{total}\mathrm{ }\mathrm{de}\mathrm{ }\mathrm{resultados}\mathrm{ }\mathrm{do}\mathrm{ }\mathrm{espaço}\mathrm{ }\mathrm{amostral}}=\frac{n\left(A\right)}{n\left(\mathrm{\Omega }\right)}$

No caso do exemplo do dado, temos que $n\left(\mathrm{\Omega }\right)=6$ e que $n\left(A\right)=1$, em que A é o evento cair a face 2; logo, a probabilidade será:

$P\left(A\right)=\frac{1}{6}\approx \mathrm{0,17}$

Ou, em porcentagem, 17%.

É importante notar que a probabilidade não pode assumir valores negativos nem superar 1. Em outras palavras, a probabilidade de ocorrência de um evento A deve estar no intervalo de 0 a 1, $0\le P\left(A\right)\le 1$, podendo ser representada em porcentagem, ou seja, $0\le P\left(A\right)\le 100\%$.

A soma das probabilidades de todos os eventos em um espaço amostral resulta em 1 ou 100%. Um aspecto relevante disso é que, quando temos a probabilidade de um evento A, podemos calcular a probabilidade do complemento desse evento. O complemento do evento A corresponde ao conjunto de todos os resultados no espaço amostral que não fazem parte do evento A.

Por exemplo, se jogarmos um dado e o evento A for “o número é menor que 5”, o complemento desse evento será “o número é maior ou igual a 5”. Em símbolos, temos: $A=\left\{\mathrm{1,2},\mathrm{3,4}\right\}$ e seu complemento $A^{\text{'}}=\left\{\mathrm{5,6}\right\}$.

Utilizando o fato de que a soma das probabilidades de todos os eventos é 1, podemos determinar a probabilidade de $A^{\text{'}}$:

$P\left(A\right)+P\left(A^{\text{'}}\right)=1$

$P\left(A^{\text{'}}\right)=1-P\left(A\right)$

$P\left(A^{\text{'}}\right)=1-\frac{4}{6}=\frac{2}{6}=\frac{1}{3}$

Siga em Frente...

Com base nos conceitos vistos até o momento, vamos resolver o exemplo 1.

 

Exemplo 1

Três cavalos (A, B e C) estão em uma corrida. A tem duas vezes mais probabilidades de ganhar que B, e B tem duas vezes mais probabilidades de ganhar que C. Quais são as probabilidades de vitória de cada um?

Temos os seguintes eventos:

• A = o cavalo A vencer.
• B = o cavalo B vencer.
• C = o cavalo C vencer.

Sabemos que A tem duas vezes mais probabilidades de ganhar que B, isto é, $P\left(A\right)=2P\left(B\right)$, e que B tem duas vezes mais probabilidades de ganhar que C, ou seja, $P\left(B\right)=2P\left(C\right)$.  Como não sabemos o valor de $P\left(C\right)$, vamos considerar que $P\left(C\right)=x$, assim temos que $P\left(B\right)=2P\left(C\right)=2x$ e que $P\left(A\right)=2P\left(B\right)=2\cdot 2x=4x$. Sabemos que a soma das probabilidades de todos os eventos de um espaço amostral é 1, logo: 

$P\left(A\right)+P\left(B\right)+P\left(C\right)=1$

$4x+2x+x=1$

$7x=1$

$x=\frac{1}{x}$

Logo, $P\left(C\right)=\frac{1}{7}$, $P\left(B\right)=\frac{2}{7}$ e $P\left(A\right)=\frac{4}{7}$.

No contexto da probabilidade, existem axiomas fundamentais que desempenham um papel crucial quando se trata de assegurar a coerência e o respeito às propriedades matemáticas fundamentais das probabilidades calculadas. Esses axiomas estabelecem o alicerce teórico indispensável para a aplicação da teoria da probabilidade em contextos práticos, tais como previsões de eventos, avaliação de riscos e processos decisórios. São axiomas da probabilidade:

• $0\le P\left(A\right)\le 1$
• $P\left(\mathrm{\Omega }\right)=1$
• Se dois eventos são mutuamente exclusivos, ou seja, não apresentam nenhuma dependência, então a probabilidade de um ou outro acontecer é a soma de suas probabilidades individuais: $P(A\cup B)=P\left(A\right)+P\left(B\right)$.

Com base nesses axiomas, podemos estabelecer os seguintes teoremas:

• A probabilidade do conjunto vazio é zero: $P\left(\varnothing \right)=0$
• A probabilidade do complementar é dada por $P\left(A^{\text{'}}\right)=1-P\left(A\right)$
• A probabilidade da reunião de dois eventos é dada por $\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P(A\cap B)$

Quando lidamos com dois eventos, eles podem ser categorizados como independentes ou dependentes. Eventos são considerados independentes quando a ocorrência de um deles não tem impacto na ocorrência do outro. Por exemplo, lançar uma moeda ao ar pode resultar em cara em uma ocasião, e esse resultado não está relacionado ao resultado anterior. Dois eventos, quando são mutuamente exclusivos, dependem um do outro para ocorrer, portanto são denominados eventos dependentes. Tomando como exemplo um jogo de cartas de baralho, se você retirar um rei de espadas na primeira tentativa, a probabilidade de retirar um rei de espadas na segunda tentativa será nula, uma vez que não há mais reis de espadas no baralho. Portanto, a probabilidade de retirar uma carta específica na segunda tentativa está condicionada à carta retirada na primeira tentativa, tornando esses eventos dependentes.

A probabilidade condicional é frequentemente confundida com a probabilidade de ocorrência de eventos dependentes. A diferença é que nos eventos dependentes estuda-se a probabilidade de ocorrências de ambos e os eventos são mutuamente exclusivos, como no exemplo anterior (Virgillito, 2017). A probabilidade condicional também estuda a ocorrência de ambos os eventos, mas desde que um deles tenha ocorrido e será dada por:

$P\left(A/B\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)} \mathrm{ou} P\left(A\cap B\right)=P\left(A/B\right)\cdot P\left(B\right)$

Lê-se: a probabilidade de o evento A acontecer se o evento B já tiver ocorrido. Quando lidamos com dois eventos independentes e desejamos calcular a probabilidade de ambos ocorrerem simultaneamente, podemos aplicar a regra da multiplicação, que estabelece que $\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)$.

Vamos analisar um problema em que é necessário empregar a probabilidade condicional.

 

Exemplo 2

Consideremos 250 alunos que cursam o primeiro ciclo de uma faculdade. Desses alunos, 100 são homens e 150 são mulheres, 110 cursam Física e 140 cursam Química. A Tabela 1 sintetiza a distribuição dos alunos.

Sexo	Física	Química	Total
Homem	40	60	100
Mulher	70	80	150
Total	110	140	250

Tabela 1 | Informações dos alunos. Fonte: elaborada pela autora.

 

Considerando que um aluno é sorteado ao acaso, qual é a probabilidade de que esteja cursando Física e seja mulher?

Vamos considerar que A seja o evento “cursar Física” e B seja o evento “ser mulher”. Assim, para encontrar a probabilidade de que um aluno esteja cursando Física e seja uma mulher, você pode usar a fórmula da probabilidade condicional:

$P\left(A/B\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}$

Primeiramente temos que determinar a probabilidade de cursar Física e ser mulher. De acordo com a Tabela 1, há 70 mulheres cursando Física. Agora, precisamos analisar a probabilidade de um aluno ser mulher, que é 150. Assim, a probabilidade de escolher um aluno que cursa Física e seja mulher é:

$P\left(A/B\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}=\frac{70}{150}=\frac{7}{15}\approx \mathrm{0,47} \mathrm{ou}\mathrm{ } 47\%$

Observe que o estudo da probabilidade condicional é crucial para lidar com a incerteza e a dependência entre eventos em uma ampla variedade de contextos, desde a ciência até a vida cotidiana, e é uma ferramenta fundamental para a tomada de decisões informadas.

Vamos Exercitar?

Agora que você já conheceu os princípios básicos da probabilidade e da probabilidade condicional, vamos retomar nossa situação inicial. Considerando um lote de peças formado por 111 peças — 100 boas, 8 com defeitos e 3 com defeitos graves —, temos que determinar a probabilidade de alguns eventos. Sabendo que uma peça é escolhida aleatoriamente, vamos determinar a probabilidade de que:

a) Ela não tenha defeitos graves.

Queremos determinar a probabilidade de que uma peça não tenha defeito grave (evento A), ou seja, a peça pode ser boa ou ter defeitos, logo são 108 peças possíveis dentre as 111 peças do lote. Assim, a probabilidade será:

$P\left(A\right)=\frac{108}{111}=\frac{36}{37}$

Ou seja, a probabilidade de que a peça não tenha defeitos graves é de aproximadamente 97%.

b) Ela não tenha defeitos.

Queremos determinar a probabilidade de que uma peça não tenha defeito (evento B), ou seja, a peça deve ser boa, logo são 100 peças possíveis dentre as 111 peças do lote. Assim, a probabilidade será:

$P\left(B\right)=\frac{100}{111}$

Ou seja, a probabilidade de que a peça não tenha defeitos é de aproximadamente 90%.

c) Ela seja boa ou tenha defeitos graves.

Nesse caso, temos duas opções: a peça ser boa (evento B) ou ter defeitos graves (evento C). A probabilidade de um dos dois eventos ocorrer será dada pela soma de cada um dos eventos, visto que são eventos mutuamente exclusivos.

$P\left(B\cup C\right)=P\left(B\right)+P\left(C\right)=\frac{100}{111}+\frac{3}{111}=\frac{103}{111}$

Ou seja, a probabilidade de que a peça seja boa ou tenha defeitos graves é de aproximadamente 93%.

Agora vamos considerar que sejam retiradas duas peças ao acaso, para determinar a probabilidade de que:

a) Ambas sejam perfeitas.

Temos que determinar a probabilidade de que tanto a primeira peça quanto a segunda sejam perfeitas. Um ponto importante que devemos considerar é que ao, retirarmos a primeira peça, nosso espaço amostral diminui uma unidade, visto que não há reposição de peças. Sabemos que a probabilidade de a peça ser perfeita, ou seja, ser boa, é $P\left(B\right)=\frac{100}{111}$. A segunda peça também deve ser boa, logo temos que diminuir uma unidade na quantidade de peças boas:

$P\left(B e B\right)=\frac{100}{111}\cdot \frac{99}{110}=\frac{9900}{12210}=\frac{30}{37}$

Ou seja, a probabilidade de que ambas as peças sejam perfeitas é de aproximadamente 81%.

b) Pelo menos uma seja perfeita.

Queremos a probabilidade de que pelo menos uma peça seja perfeita, o que nos leva às seguintes possibilidades:

• A primeira peça é boa e a segunda peça é boa:

$P\left(B e B\right)=\frac{100}{111}\cdot \frac{99}{110}=\frac{9900}{12210}=\frac{30}{37}$

• A primeira peça é boa e a segunda peça tem defeito (evento D): 

$P\left(B e D\right)=\frac{100}{111}\cdot \frac{8}{110}=\frac{800}{12210}=\frac{80}{1221}$

• A primeira peça é boa e a segunda tem defeito grave:

$P\left(B e C\right)=\frac{100}{111}\cdot \frac{3}{110}=\frac{300}{12210}=\frac{10}{407}$

• A primeira peça tem defeito grave e a segunda peça é boa:

$P\left(C e B\right)=\frac{3}{111}\cdot \frac{100}{110}=\frac{300}{12210}=\frac{10}{407}$

• A primeira peça tem defeito e a segunda peça é boa: 

$P\left(D e B\right)=\frac{8}{111}\cdot \frac{100}{110}=\frac{800}{12210}=\frac{80}{1221}$

Somando essas probabilidades, teremos a probabilidade de que pelo menos uma seja perfeita:

$\frac{30}{37}+\frac{80}{1221}+\frac{10}{407}+\frac{10}{407}+\frac{80}{1221}=\frac{110}{111}$

Ou seja, a probabilidade que pelo menos uma peça seja perfeita é de aproximadamente 99%.

c) Nenhuma tenha defeito grave.

Queremos a probabilidade de que nenhuma peça tenha defeito grave, o que nos leva às seguintes possibilidades:

• A primeira peça é boa e a segunda peça é boa:

$P\left(B e B\right)=\frac{100}{111}\cdot \frac{99}{110}=\frac{9900}{12210}=\frac{30}{37}$

• A primeira peça é boa e a segunda peça tem defeito (evento D):

$P\left(B e D\right)=\frac{100}{111}\cdot \frac{8}{110}=\frac{800}{12210}=\frac{80}{1221}$

• A primeira peça tem defeito e a segunda peça é boa:

$P\left(D e B\right)=\frac{8}{111}\cdot \frac{100}{110}=\frac{800}{12210}=\frac{80}{1221}$

• A primeira peça tem defeito e a segunda peça tem defeito: 

$P\left(D e D\right)=\frac{8}{111}\cdot \frac{7}{110}=\frac{56}{12210}=\frac{28}{6105}$

Somando essas probabilidades teremos a probabilidade de nenhuma peça ter defeito grave:

$\frac{30}{37}+\frac{80}{1221}+\frac{80}{1221}+\frac{28}{6105}=\frac{1926}{2035}$

Ou seja, a probabilidade de que nenhuma peça tenha defeito grave é de aproximadamente 95%.

d) Nenhuma seja perfeita.

Queremos a probabilidade de que nenhuma peça seja boa, o que nos leva às seguintes possibilidades:

• A primeira peça tem defeito a segunda peça tem defeito (evento D): 

$P\left(D e D\right)=\frac{8}{111}\cdot \frac{7}{110}=\frac{56}{12210}=\frac{28}{6105}$

• A primeira peça tem defeito e a segunda peça tem defeito grave: 

$P\left(D e C\right)=\frac{8}{111}\cdot \frac{3}{110}=\frac{24}{12210}=\frac{4}{2035}$

• A primeira peça tem defeito grave e a segunda peça tem defeito:

$P\left(C e D\right)=\frac{3}{111}\cdot \frac{8}{110}=\frac{24}{12210}=\frac{4}{2035}$

• A primeira peça tem defeito grave a segunda peça tem defeito grave:

$P\left(C e C\right)=\frac{3}{111}\cdot \frac{2}{110}=\frac{6}{12210}=\frac{1}{2035}$

Somando essas probabilidades, teremos a probabilidade de nenhuma peça ser perfeita:

$\frac{28}{6105}+\frac{4}{2035}+\frac{4}{2035}+\frac{1}{2035}=\frac{1}{111}$

Ou seja, a probabilidade de que nenhuma peça seja perfeita é de aproximadamente 0,90%.

É importante notar que os problemas de probabilidade frequentemente requerem uma interpretação cuidadosa. Portanto, ao enfrentar esses problemas, é fundamental ler com atenção as informações apresentadas e ser cauteloso ao efetuar os cálculos.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre o cálculo de probabilidades, recomendamos que você leia o capítulo 8 do livro Estatística. Em seguida, escolha alguns exercícios para resolver. Fique tranquilo, pois as respostas para esses exercícios estão disponíveis ao final de cada lista de problemas.

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023. 

Distribuição binomial

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! A aplicação das distribuições de probabilidade desempenha um papel fundamental em estatística, probabilidade e uma variedade de disciplinas científicas e de engenharia por várias razões. Por exemplo, as distribuições de probabilidade são essenciais para conduzir a inferência estatística, que compreende a estimativa de parâmetros desconhecidos, a realização de testes de hipóteses e a construção de intervalos de confiança com base em amostras de dados. Em muitos casos, a forma da distribuição da estatística de amostra é conhecida, o que permite realizar inferências precisas.

Em resumo, as distribuições de probabilidade são ferramentas poderosas para compreender, modelar e enfrentar a incerteza e a variabilidade em uma ampla gama de aplicações, abrangendo desde análises estatísticas até previsões e o processo de tomada de decisões.

Nesta aula, estudaremos o que é uma distribuição de probabilidade e exploraremos as características da distribuição binomial. Para entender melhor como podemos aplicar esse conceito, imagine um experimento com uma moeda não viciada. Considerando que ela seja jogada 10 vezes, vamos determinar a probabilidade:

1. De ocorrerem 6 caras.
2. De ocorrerem pelo menos 2 caras.
3. De não ocorrer coroa.
4. De ocorrerem pelo menos uma coroa.

Para isso, é fundamental compreender o conceito de variável aleatória e saber calcular uma distribuição binomial.

Bons estudos!

Vamos Começar!

Considere o espaço amostral de um lançamento de um dado e a observação da face superior, representado por S = {1, 2, 3, 4, 5, 6}. Esse espaço amostral é composto de números reais. Agora, considere o espaço amostral de um lançamento de uma moeda e a observação da face superior, representado por S = {cara, coroa}. Nesse caso, o espaço amostral não é composto de números reais.

Observe que, no espaço amostral do lançamento de um dado, podemos aplicar recursos estatísticos, como média, variância e desvio-padrão, conceitos da Estatística Descritiva. No entanto, no caso do lançamento de uma moeda, não faz sentido estabelecer média, variância e desvio-padrão, uma vez que os elementos do espaço amostral não são valores numéricos. De maneira geral, quando o espaço amostral de um experimento não é composto de números reais, não é possível utilizar diretamente os recursos da Estatística Descritiva. Para que esses recursos possam ser aplicados, é necessário definir uma função que mapeie o espaço amostral não numérico em um espaço amostral numérico. Esse é o objetivo da definição de variável aleatória (Silva et al., 2018).

Seja em um experimento cujo espaço amostral é dado por $\mathrm{\Omega }=\{a_1, a_2, a_3\dots , a_n\}$, “qualquer função x que transforma os valores $a_1, a_2, a_3\dots , a_n$ em números reais é chamada variável aleatória discreta” (Silva et al., 2018, p. 137). Por exemplo, no lançamento de uma moeda, a variável aleatória $X$ retorna o número de caras que pode ser obtido no lançamento da moeda, ou seja, $X=0$, quando se obtém coroa e $X=1$ quando se obtém cara.

As probabilidades relacionadas a diferentes resultados em um espaço amostral se traduzem em probabilidades específicas associadas aos valores de qualquer instância particular da variável aleatória $X$. A distribuição de probabilidade de $X$ revela como a probabilidade total de 1 se divide entre os diferentes valores potenciais de $X$ (Devore, 2018). Por exemplo, vamos considerar o lançamento de duas moedas. Se definirmos que a variável aleatória $X$ é a quantidade possível de caras nesse lançamento, temos que $X$ pode ser igual a 0, 1 e 2. A distribuição de probabilidade nos fornecerá informações sobre como a probabilidade total de 1 é distribuída entre os três valores possíveis. Utilizaremos a seguinte notação para as probabilidades na distribuição:

$p\left(0\right)=\mathrm{probabilidade}\mathrm{ }\mathrm{de}\mathrm{ }X\mathrm{ }\mathrm{valer}\mathrm{ }0=P(X=0)$

$p\left(1\right)=\mathrm{probabilidade}\mathrm{ }\mathrm{de}\mathrm{ }X\mathrm{ }\mathrm{valer}\mathrm{ }1=P(X=1)$

$p\left(2\right)=\mathrm{probabilidade}\mathrm{ }\mathrm{de}\mathrm{ }X\mathrm{ }\mathrm{valer}\mathrm{ }2=P(X=2)$

$⋮$

$p\left(x\right)=\mathrm{probabilidade}\mathrm{ }\mathrm{de}\mathrm{ }X\mathrm{ }\mathrm{valer}\mathrm{ }x=P(X=x)$

De acordo com o tipo de variável aleatória, existem diferentes distribuições de probabilidade. Quando a variável aleatória é discreta, temos as distribuições discretas de probabilidade, e quando as variáveis aleatórias são contínuas, temos as distribuições contínuas de probabilidade. Neste momento, nosso foco é a distribuição binomial, um exemplo de distribuição discreta.

Siga em Frente...

A distribuição binomial é provavelmente a distribuição teórica mais simples possível. É aplicada a cenários em que pode haver dois resultados. Tradicionalmente, esses dois resultados são rotulados como “sucesso” e “fracasso”, embora essa designação seja arbitrária. De forma mais ampla, um dos eventos, chamado “sucesso”, é representado pelo número 1, enquanto o outro evento, chamado “fracasso”, é representado pelo número zero. A variável aleatória de interesse, denotada como $X$, corresponde ao número de ocorrências do evento em determinado número de tentativas. O número de tentativas, $n$, pode ser qualquer inteiro positivo, e a variável $X$ pode assumir valores não negativos inteiros, variando de 0 (se o evento de interesse não ocorrer em nenhuma das $n$ tentativas) a $n$ (se ocorrer em todas as ocasiões). A distribuição binomial pode ser utilizada para calcular probabilidades para cada um desses $n+1$ possíveis valores de $X$, desde que as seguintes condições sejam atendidas:

• A probabilidade de o evento ocorrer não mudar de tentativa para tentativa.
• As saídas ou os resultados das n tentativas serem mutuamente independentes.

A distribuição de probabilidade binomial será dada por:

$\mathit{P}\left(\mathit{x}\right)=\mathit{P}\left(\mathit{X}=\mathit{x}\right)={\mathit{C}}_{\mathit{n}}^{\mathit{x}}\cdot {\mathit{p}}^{\mathit{x}}\cdot {\mathit{q}}^{\mathit{n}-\mathit{x}}$

em que:

$P\left(x\right)$ é a probabilidade de que o evento se realize  vezes em tentativas.

$C_n^x=\frac{n!}{x!\left(n-x\right)!}$

$p$ é a probabilidade de que o evento se realize em uma só tentativa, ou seja, a probabilidade de se ter sucesso.

$q=1-p$é a probabilidade de que o evento não se realize, ou seja, a probabilidade de se ter fracasso.

Quando lidamos com uma distribuição discreta de probabilidade, é possível calcular a média (esperança) e o desvio-padrão da distribuição. No contexto da distribuição binomial, temos o seguinte:

$\mu \left(x\right)=n\cdot p$

$\sigma =\sqrt{n\cdot p\cdot q}$

Com base nos conceitos que discutimos até agora, vamos explorar um exemplo.

 

Exemplo

Consideremos que certo time de voleibol tem 2/3 de probabilidade de vitória sempre que joga. Se esse time jogar 5 partidas, qual é a probabilidade de esse time vencer pelo menos duas partidas?

Observe que são realizadas 5 tentativas, em cada uma das quais apenas um sucesso ou fracasso é possível, e essas tentativas são independentes umas das outras. Dadas essas características, podemos aplicar a distribuição binomial. É importante destacar que a questão requer a probabilidade de vencer pelo menos duas partidas, o que implica vencer 2, 3, 4 ou 5 partidas. Portanto, precisamos calcular a probabilidade para cada uma dessas situações e, em seguida, somar essas probabilidades.

A variável aleatória “vencer a partida” será denotada por $X$. Sabemos que $n=5$, e que a probabilidade de vencer é 2/3, ou seja, $p=\frac{2}{3}$. Logo, a probabilidade de não vencer é $q=1-p=1-\frac{2}{3}=\frac{1}{3}$. Com base nessas informações, temos:

$\mathit{P}\left(\mathit{x}\right)=\mathit{P}\left(\mathit{X}=\mathit{x}\right)={\mathit{C}}_{\mathit{n}}^{\mathit{x}}\cdot {\mathit{p}}^{\mathit{x}}\cdot {\mathit{q}}^{\mathit{n}-\mathit{x}}$

$P\left(2\right)=P\left(X=2\right)=C_5^2\cdot {\left(\frac{2}{3}\right)}^2\cdot {\left(\frac{1}{3}\right)}^{5-2}=\frac{5!}{2!\left(5-2\right)!}\cdot {\left(\frac{2}{3}\right)}^2\cdot {\left(\frac{1}{3}\right)}^3=10\cdot \frac{4}{9}\cdot \frac{1}{27}=\frac{40}{243}$

$P\left(3\right)=P\left(X=3\right)=C_5^3\cdot {\left(\frac{2}{3}\right)}^3\cdot {\left(\frac{1}{3}\right)}^{5-3}=\frac{5!}{3!\left(5-3\right)!}\cdot {\left(\frac{2}{3}\right)}^3\cdot {\left(\frac{1}{3}\right)}^2=10\cdot \frac{8}{27}\cdot \frac{1}{9}=\frac{80}{243}$

$P\left(4\right)=P\left(X=4\right)=C_5^4\cdot {\left(\frac{2}{3}\right)}^4\cdot {\left(\frac{1}{3}\right)}^{5-4}=\frac{5!}{4!\left(5-4\right)!}\cdot {\left(\frac{2}{3}\right)}^4\cdot {\left(\frac{1}{3}\right)}^1=5\cdot \frac{16}{81}\cdot \frac{1}{3}=\frac{80}{243}$

$P\left(5\right)=P\left(X=5\right)=C_5^5\cdot {\left(\frac{2}{3}\right)}^5\cdot {\left(\frac{1}{3}\right)}^{5-5}=\frac{5!}{5!\left(5-5\right)!}\cdot {\left(\frac{2}{3}\right)}^5\cdot {\left(\frac{1}{3}\right)}^0=1\cdot \frac{32}{243}\cdot 1=\frac{32}{243}$

A probabilidade de vencer ao menos 2 partidas será:

$P\left(X\ge 2\right)=P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)$

$P\left(X\ge 2\right)=\frac{40}{243}+\frac{80}{243}+\frac{80}{243}+\frac{32}{243}=\frac{232}{243}\approx \mathrm{0,95}$

Ou seja, aproximadamente 95%.

Esse problema pode ser abordado considerando o princípio de que a soma total das probabilidades é igual a 1. Se desejamos calcular a probabilidade de vencer pelo menos duas partidas, isso significa que não estamos interessados na probabilidade de vencer nenhuma partida ou apenas uma partida. Subtraindo a soma das probabilidades de vencer nenhuma partida ou uma partida de 1, obteremos a probabilidade de vencer pelo menos duas partidas, ou seja, $P\left(X\ge 2\right)=1-[P\left(X=0\right)+P\left(X=1\right)]$. Explore essa abordagem e você verá que chegará ao mesmo resultado obtido anteriormente.

Vamos Exercitar?

Agora que você já conheceu os princípios relacionados à distribuição de probabilidade binomial, vamos retomar nossa situação inicial. Nela, jogamos uma moeda 10 vezes e queremos determinar algumas probabilidades. Se considerarmos a variável aleatória “ocorrer cara”, há apenas duas possibilidades: ou ocorre cara ou ocorre coroa. Além disso, o experimento foi realizado em 10 tentativas, e essas tentativas são independentes umas das outras. Dadas essas características, podemos aplicar a distribuição binomial. Considerando que a variável aleatória seja $X=$“ocorrer cara”, temos as seguintes informações:

$P\left(X=x\right)={\mathit{C}}_{\mathit{n}}^{\mathit{x}}\cdot {\mathit{p}}^{\mathit{x}}\cdot {\mathit{q}}^{\mathit{n}-\mathit{x}} \left\{\begin{array}{c}p=\frac{1}{2} \\ q=1-p=\frac{1}{2}\\ n=10\end{array}\right.$

Com base nessas informações, vamos calcular as probabilidades solicitadas:

a) De ocorrerem 6 caras.

Queremos a probabilidade de que ocorram 6 caras:

$P\left(6\right)=P\left(X=6\right)=C_{10}^6\cdot {\left(\frac{1}{2}\right)}^6\cdot {\left(\frac{1}{2}\right)}^{10-6}=\frac{10!}{6!\left(10-6\right)!}\cdot {\left(\frac{1}{2}\right)}^6\cdot {\left(\frac{1}{2}\right)}^4=210\cdot \frac{1}{64}\cdot \frac{1}{16}=\frac{210}{1024}\approx \mathrm{0,21}$

Ou seja, aproximadamente 21%.

b) De ocorrerem pelo menos 2 caras.

A probabilidade de ocorrerem menos duas caras requer o cálculo da probabilidade de ocorrerem 2, 3, 4, 5, 6, 7, 8, 9 ou 10 caras. Uma opção é calcular a probabilidade para cada uma das possibilidades e depois somar. Mas perceba que isso seria trabalhoso. Esse problema pode ser abordado considerando-se o princípio de que a soma total das probabilidades é igual a 1. Se desejamos calcular a probabilidade de ocorrerem pelo menos duas caras, isso significa que não estamos interessados na probabilidade de não ocorrer nenhuma cara ou de ocorrer apenas uma cara. Subtraindo a soma das probabilidades de não ocorrer cara e ocorrer uma cara de 1, obteremos a probabilidade de ocorrerem pelo menos duas caras, ou seja, $\left(X\ge 2\right)=1-[P\left(X=0\right)+P\left(X=1\right)]$. Vamos calcular essas probabilidades:

$P\left(0\right)=P\left(X=0\right)=C_{10}^0\cdot {\left(\frac{1}{2}\right)}^0\cdot {\left(\frac{1}{2}\right)}^{10-0}=\frac{10!}{0!\left(10-0\right)!}\cdot {\left(\frac{1}{2}\right)}^0\cdot {\left(\frac{1}{2}\right)}^{10}=1\cdot 1\cdot \frac{1}{1024}=\frac{1}{1024}$

$P\left(1\right)=P\left(X=1\right)=C_{10}^1\cdot {\left(\frac{1}{2}\right)}^1\cdot {\left(\frac{1}{2}\right)}^{10-1}=\frac{10!}{1!\left(10-1\right)!}\cdot {\left(\frac{1}{2}\right)}^1\cdot {\left(\frac{1}{2}\right)}^9=10\cdot \frac{1}{2}\cdot \frac{1}{512}=\frac{10}{1024}$

$P\left(X\ge 2\right)=1-\left[\frac{1}{1024}+\frac{10}{1024}\right]=1-\frac{11}{1024}=\frac{1013}{1024}\approx \mathrm{0,99}$

Ou seja, aproximadamente 99%.

c) De não ocorrer coroa.

Nossa variável aleatória é a “ocorrência de cara", portanto a ausência de coroa só ocorrerá quando obtivermos 10 caras.

$P\left(10\right)=P\left(X=10\right)=C_{10}^{10}\cdot {\left(\frac{1}{2}\right)}^{10}\cdot {\left(\frac{1}{2}\right)}^{10-10}=\frac{10!}{0!\left(10-0\right)!}\cdot {\left(\frac{1}{2}\right)}^{10}\cdot {\left(\frac{1}{2}\right)}^0=1\cdot \frac{1}{1024}\cdot 1=\frac{1}{1024}\approx \mathrm{0,00098}$

Ou seja, aproximadamente 0,098%.

d) De ocorrer pelo menos uma coroa.

Nossa variável aleatória é a “ocorrência de cara”. Logo, para ocorrer pelo menos uma coroa, temos que excluir a possibilidade de não ocorrer nenhuma coroa, que nesse caso é a ocorrência de 10 caras. Assim, a probabilidade de ocorrer pelo menos uma coroa será:

$P\left(X\le 9\right)=1-P(X=10)$

$=1-\frac{1}{1024}=\frac{1023}{1024}\approx \mathrm{0,99}$

Ou seja, aproximadamente 99%.

Para resolver problemas que envolvem a distribuição binomial, é possível empregar diferentes estratégias, dependendo da interpretação do problema. Leia as questões com cuidado e tenha em mente que a soma de todas as probabilidades sempre será igual a 1.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre as distribuições discretas de probabilidade, mais especificamente, a distribuição binomial, sugerimos a leitura da seção 4.2 do livro $https://plataforma.bvirtual.com.br/Acervo/Publicacao/36874$. Após concluir a leitura do capítulo, escolha alguns exercícios para resolver!

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023.

Distribuição de Poisson

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Você já estudou a distribuição de probabilidade binominal, utilizada quando um experimento envolve eventos independentes que podem ser classificados como sucesso ou fracasso e estamos interessados em calcular a probabilidade de certo número de sucessos em um número fixo de tentativas.

Nesta aula, exploraremos outro tipo de distribuição discreta de probabilidade: a distribuição de Poisson. Essa distribuição é utilizada em experimentos nos quais estamos interessados não no número de sucessos em certo número de tentativas, mas sim no número de sucessos ao longo de um intervalo contínuo, que pode ser definido em termos de tempo, espaço ou outros parâmetros.

Para ilustrar como podemos aplicar esse conceito, suponha que o engenheiro encarregado da produção em uma fábrica de pneus decidiu testar a qualidade dos pneus fabricados. Para esse fim, conduziu testes na pista e constatou que, em média, um pneu estourava a cada 5 mil quilômetros. Com base nesses dados, responda:

1. Qual é a probabilidade de que um carro ande 5 mil quilômetros sem nenhum pneu estourar?
2. Qual é a probabilidade de que, em um teste de 3 mil quilômetros, haja dois pneus estourados?

Para isso, é essencial compreender as características da distribuição de Poisson e saber como realizar seu cálculo.

Bons estudos!

Vamos Começar!

Imagine que você tenha acabado de chegar em uma parada de ônibus e ser informado de que os ônibus para o destino que você deseja passam a cada intervalo de 15 minutos. Agora, você se pergunta sobre a probabilidade de um ônibus se aproximar nos próximos 10 minutos. Se alguém lhe disser que o último ônibus passou há apenas um minuto, suas expectativas são baixas, mas se o último ônibus passou há mais de 12 minutos, suas expectativas são consideravelmente mais elevadas. À medida que o tempo decorrido desde a última ocorrência aumenta, a expectativa de uma nova ocorrência também aumenta.

A variável aleatória que permite calcular a probabilidade desse tipo de ocorrência tem distribuição de Poisson. A distribuição de Poisson é utilizada em estudos nos quais o enfoque não reside na contagem de sucessos em um número específico de tentativas, como é o caso da distribuição binomial, mas sim na quantificação dos sucessos ocorridos durante um período contínuo, que pode ser um intervalo de tempo, espaço, entre outros. É uma distribuição de probabilidade discreta utilizada para descrever a ocorrência de eventos em intervalos específicos. A variável aleatória representa o número de vezes que o evento ocorre nesse intervalo (Silva et al., 2018). A distribuição de Poisson é dada por:

$\mathit{P}\left(\mathit{x}\right)=\mathit{P}\left(\mathit{X}=\mathit{x}\right)=\frac{{\mathit{e}}^{-\mathit{\lambda }}\cdot {\mathit{\lambda }}^{\mathit{x}}}{\mathit{x}!}$

em que $\lambda$ é o número médio de ocorrências por intervalo unitário de referência.

No caso da distribuição de Poisson, a média (esperança) e o desvio-padrão são dados por:

$\mu \left(X\right)=\lambda$

$\sigma \left(X\right)=\sqrt{\lambda }$

Com base nos conceitos que discutimos até agora, vamos abordar um exemplo.

 

Exemplo

Considere que uma máquina apresenta, em média, uma peça com defeito a cada 100 peças fabricadas. Com base nessas informações, determine:

1. A probabilidade de, em um lote de 100 peças fabricadas por essa máquina, não existir nenhuma peça defeituosa.
2. A probabilidade de, em um lote de 200 peças fabricadas por essa máquina, não existir nenhuma peça defeituosa.
3. A probabilidade de, em um lote de 50 peças fabricadas por essa máquina, não existir nenhuma peça defeituosa.
4. A probabilidade de, em um lote de 100 peças fabricadas por essa máquina, existirem 3 ou mais peças defeituosas.

 

Solução

a) Inicialmente, é necessário determinar a média de ocorrências por unidade de referência, que, nesse caso, é de 1 peça defeituosa a cada 100 peças. É importante notar que o problema busca a probabilidade de não haver nenhuma peça defeituosa em um lote de 100 peças e, como o intervalo de referência é igual ao apresentado no problema, temos que $\lambda =1$. Logo:

$P\left(x\right)=P\left(X=x\right)=\frac{e^{-\lambda }\cdot {\lambda }^x}{x!}$

$P\left(0\right)=P\left(X=0\right)=\frac{e^{-1}\cdot {\left(1\right)}^0}{0!}=\frac{e^{-1}\cdot 1}{1}\approx \mathrm{0,37}$

Ou seja, aproximadamente 37%.

b) O desafio consiste em calcular a probabilidade de que, em um lote de 200 peças, nenhuma delas seja defeituosa. É importante notar que o intervalo de referência difere do intervalo mencionado no enunciado. Para encontrar a média de peças defeituosas no novo intervalo, podemos empregar uma regra de três:

$1 peça---------100 peças$

$z peças--------200 peças$

$z\cdot 100=1\cdot 200$

$z=\frac{200}{100}=2$

Portanto, $\lambda =2$. Agora, vamos calcular a probabilidade de, em um lote de 200 peças, nenhuma ser defeituosa:

$P\left(x\right)=P\left(X=x\right)=\frac{e^{-\lambda }\cdot {\lambda }^x}{x!}$

$P\left(0\right)=P\left(X=0\right)=\frac{e^{-2}\cdot {\left(2\right)}^0}{0!}=\frac{e^{-2}\cdot 1}{1}\approx \mathrm{0,14}$

Ou seja, aproximadamente 14%.

c) Temos que determinar a probabilidade de que, em um lote de 50 peças, nenhuma seja defeituosa. Nesse exemplo, o intervalo de referência também difere do intervalo mencionado no enunciado, então primeiro temos que determinar o número médio de peças defeituosas nesse intervalo.

$1 peça---------100 peças$

$z peças--------50 peças$

$z\cdot 100=1\cdot 50$

$z=\frac{50}{100}=\mathrm{0,5}$

Logo, $\lambda =\mathrm{0,5}$. A probabilidade será:

$P\left(x\right)=P\left(X=x\right)=\frac{e^{-\lambda }\cdot {\lambda }^x}{x!}$

$P\left(0\right)=P\left(X=0\right)=\frac{e^{-\mathrm{0,5}}\cdot {\left(\mathrm{0,5}\right)}^0}{0!}=\frac{e^{-\mathrm{0,5}}\cdot 1}{1}\approx \mathrm{0,61}$

Ou seja, aproximadamente 61%.

d) É necessário calcular a probabilidade de que, em um lote de 100 peças, existam 3 ou mais peças defeituosas. Não é prático calcular a probabilidade de exatamente 3, 4, ..., 100 peças defeituosas e somá-las. Em vez disso, podemos adotar a abordagem de que a probabilidade de existirem 3 ou mais peças defeituosas é igual a 1 menos a probabilidade de existirem menos de 3 peças defeituosas. Portanto:

$P\left(X\ge 3\right)=1-\left(P\left(X=2\right)+P\left(X=1\right)+P\left(X=0\right)\right)$

$P\left(X\ge 3\right)=1-\left[\frac{e^{-1}\cdot {\left(1\right)}^2}{2!}+\frac{e^{-1}\cdot {\left(1\right)}^1}{1!}+\frac{e^{-1}\cdot {\left(1\right)}^0}{0!}\right]$

$P\left(X\ge 3\right)=1-\left[\mathrm{0,18}+\mathrm{0,37}+\mathrm{0,37}\right]$

$P\left(X\ge 3\right)=1-\mathrm{0,92}=\mathrm{0,08}$

Ou seja, aproximadamente 8%.

Siga em Frente...

Você já foi apresentado às duas distribuições discretas de probabilidade mais importantes. Saberia destacar as diferenças fundamentais entre essas distribuições?

• Na distribuição de Poisson, a variável aleatória representa o número de eventos em um intervalo de tempo ou espaço contínuo. Na distribuição binomial, a variável aleatória representa o número de sucessos (ou fracassos) em um número fixo de tentativas independentes.
• Na distribuição de Poisson, é definida apenas uma taxa média $\left(\lambda \right)$ que representa a taxa de ocorrência média do evento no intervalo de interesse. Na distribuição binomial, são necessários dois parâmetros: o número de tentativas $\left(n\right)$ e a probabilidade de sucesso em cada tentativa $\left(p\right)$.
• Na distribuição binomial, os valores possíveis da variável aleatória $X$ compreendem $0, 1, 2,\cdots , n$, enquanto a distribuição de Poisson inclui os valores de $X$ a partir de $0, 1, 2, \dots$ sem um limite superior específico.
• Na distribuição de Poisson, o número de ensaios (ou tentativas) não é fixo e pode ser qualquer número positivo, enquanto na distribuição binomial o número de ensaios é fixo e predefinido.
• A distribuição de Poisson é frequentemente usada para modelar eventos raros, como acidentes de trânsito em uma cidade. A distribuição binomial é aplicada quando se deseja calcular a probabilidade de um número específico de sucessos em um número fixo de ensaios independentes, como lançar uma moeda várias vezes.

Em resumo, as principais diferenças entre as distribuições de Poisson e binomial estão relacionadas à natureza das variáveis aleatórias, aos parâmetros envolvidos e à aplicação em diferentes cenários.

Vamos Exercitar?

Agora que você já conheceu os princípios relacionados à distribuição de probabilidade de Poisson, vamos retomar nossa situação inicial. Esta consiste em determinar a probabilidade de estouro de pneus considerando-se que, em um teste, contatou-se que, em média, um pneu estoura a cada 5 mil quilômetros. É importante notar que o problema nos fornece a taxa média de ocorrência do evento no intervalo de 5 mil quilômetros, um parâmetro fundamental na caracterização da distribuição de Poisson.

a) O primeiro item solicita que determinemos a probabilidade de que um carro ande 5 mil quilômetros sem nenhum pneu estourar. Observe que o intervalo de referência é o mesmo informado no enunciado do problema. Sabemos que um pneu estourava a cada 5 mil quilômetros, assim $\lambda =1$, e a probabilidade será:

$P\left(x\right)=P\left(X=x\right)=\frac{e^{-\lambda }\cdot {\lambda }^x}{x!}$

$P\left(0\right)=P\left(X=0\right)=\frac{e^{-1}\cdot {\left(1\right)}^0}{0!}=\frac{e^{-1}\cdot 1}{1}\approx \mathrm{0,37}$

Ou seja, a probabilidade de que, em 5 mil quilômetros, nenhum pneu estoure é de aproximadamente 37%.

b) No segundo item, temos que calcular a probabilidade de que, em um teste de 3 mil quilômetros, haja dois pneus estourados. Observe que o intervalo de referência difere do intervalo do enunciado. Para encontrar a média de pneus estourados no novo intervalo, podemos empregar uma regra de três:

$1 pneu---------5000 km$

$z pneus--------3000 km$

$z\cdot 5000=1\cdot 3000$

$z=\frac{3000}{5000}=\mathrm{0,6}$

Portanto, $\lambda =\mathrm{0,6}$. Agora, vamos calcular a probabilidade de que, em um teste de 3 mil quilômetros, haja dois pneus estourados:

$P\left(x\right)=P\left(X=x\right)=\frac{e^{-\lambda }\cdot {\lambda }^x}{x!}$

$P\left(2\right)=P\left(X=2\right)=\frac{e^{-\mathrm{0,6}}\cdot {\left(\mathrm{0,6}\right)}^2}{2!}\approx \mathrm{0,099}$

Ou seja, a probabilidade é de aproximadamente 9,9%.

Ao resolver problemas que envolvem a distribuição de Poisson, é importante ter cuidado com a ordem das operações. Lembre-se de que a potenciação deve ser resolvida primeiro, seguida pela multiplicação e, por fim, a divisão. Isso é fundamental para garantir cálculos precisos e corretos ao lidar com essa distribuição de probabilidade.

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre a distribuição de Poisson, sugerimos que leia a seção 10.4 do livro Estatística. Após concluir a leitura do capítulo, escolha alguns exercícios para resolver. Fique tranquilo, pois as respectivas respostas estão disponíveis ao final de cada lista de problemas.

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023. 

Distribuição normal

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante!

Esperamos que esteja bem! Você já teve a oportunidade de explorar duas distribuições de probabilidade cruciais: a distribuição binomial e a distribuição de Poisson, ambas caracterizadas por variáveis aleatórias discretas. Agora, é o momento de se familiarizar com outra distribuição igualmente relevante, porém contínua: a distribuição normal.

Também conhecida como distribuição gaussiana, a distribuição normal é, incontestavelmente, a distribuição contínua mais fundamental. Por esse motivo, dedicaremos tempo a seu estudo. Sua importância advém de diversos fatores; um deles é o Teorema Central do Limite. Esse teorema é um resultado fundamental em aplicações práticas e teóricas, pois estabelece que, mesmo quando os dados não seguem uma distribuição normal, a média deles tende a convergir para uma distribuição normal à medida que o tamanho da amostra aumenta.

Para visualizar como podemos aplicar esse conceito, suponha que certa empresa de celulares fez um estudo a respeito da vida útil de suas baterias e constatou uma duração com distribuição normal com média de 8 horas e desvio-padrão de 2 horas. Escolhendo aleatoriamente um celular produzido por essa empresa, determine:

1. A probabilidade de a bateria durar menos que 7 horas.
2. A probabilidade de a bateria durar mais que 7 horas.
3. A probabilidade de a bateria durar entre 7 e 10 horas.

Para calcular essas probabilidades, é essencial compreender as características da distribuição normal padrão e saber como realizar seu cálculo.

Bons estudos!

Vamos Começar!

Uma variável aleatória discreta é aquela cujo conjunto de valores possíveis é finito ou infinito, o que significa que a variável pode assumir apenas um número específico de valores distintos. Por outro lado, uma variável aleatória contínua é aquela cujo conjunto de valores possíveis forma um intervalo contínuo de números reais. Os valores possíveis de uma variável aleatória contínua podem assumir qualquer valor em um intervalo específico e geralmente incluem números decimais. Por exemplo, a altura de indivíduos em uma população, o tempo para concluir uma tarefa e a temperatura em determinado local em dado momento.

Uma distribuição contínua de probabilidade, ou simplesmente uma distribuição contínua, descreve o comportamento de uma variável aleatória contínua. Uma distribuição contínua é caracterizada por sua função de densidade de probabilidade (FDP), uma função matemática que atribui probabilidades a diferentes valores da variável aleatória contínua. A função de densidade de probabilidade é definida de modo que a área sob a curva da função em um intervalo específico corresponde à probabilidade de que a variável aleatória esteja nesse intervalo.

Dentro da variedade de distribuições contínuas, encontramos a distribuição normal. A distribuição normal é uma distribuição de probabilidade contínua aplicada a uma variável aleatória cuja representação gráfica é caracterizada por uma curva normal, satisfazendo as propriedades listadas a seguir:

• A média, a mediana e a moda são iguais.
• Uma curva normal tem forma de sino e é simétrica em torno da média (Figura 1).
• A área total sob a curva normal é igual a 1.
• A variável aleatória $X$ pode assumir todo e qualquer valor real.
• A probabilidade de a variável aleatória $X$ ter valores maiores que a média é igual à probabilidade de ter valores menores que a média (ambas as probabilidades são 0,5).
• À medida que a curva normal se distancia da média, ela se aproxima do eixo $x$, mas sem o tocar (Larson; Farber, 2015).

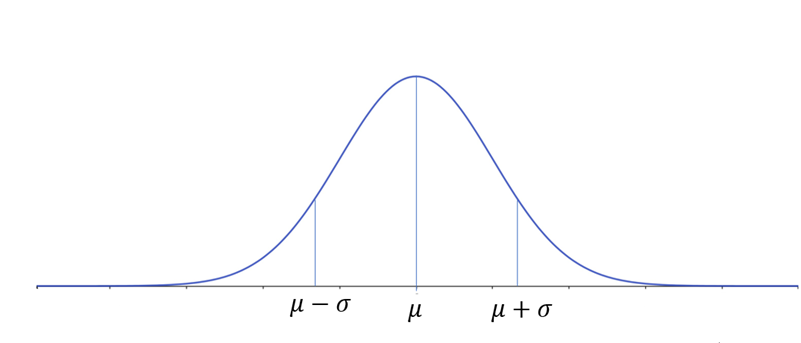
A probabilidade de uma variável aleatória assumir um valor em determinado intervalo é dada por:

$P\left(x_1\le X\le x_2\right)={\int }_{x_1}^{x_2}\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2}dx$

Em que a função densidade de probabilidade é $\frac{1}{\sigma \sqrt{2\pi {\sigma }^2}}{e}^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2}$.

Com o objetivo de simplificar o cálculo dessa integral, foi desenvolvida uma abordagem que a transforma um único caso de uma função de distribuição normal $N(\mu ,\sigma )$ em uma função de distribuição normal padrão, na qual $\mu =0$ e o desvio-padrão $\sigma =1$. Essa função de distribuição normal padronizada é denotada como $N\left(\mathrm{0,1}\right)$.

Uma vez que é possível padronizar qualquer distribuição normal, você pode empregar o z-escore e a curva normal padrão para calcular áreas (e, por consequência, probabilidades) sob qualquer curva normal (Larson; Farber, 2015). O z-escore será dado pela fórmula:

$\mathit{z}=\frac{\mathbf{valor}-\mathbf{m}\mathit{é}\mathbf{dia}}{\mathbf{desvio}\mathbf{ }\mathbf{padrão}}$

$\mathit{z}=\frac{\mathit{x}-\mathit{\mu }}{\mathit{\sigma }}$

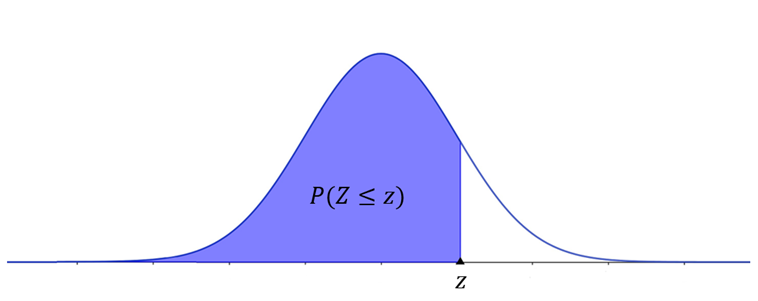
Após encontrar o z-escore, você deve encontrar a área referente a esse valor; para isso, você pode utilizar uma Tabela da Distribuição Normal Padrão (ou tabela Z – Tabela 1). Vamos apresentar a tabela z acumulada, isto é, a tabela fornece a área menor que o z-escore encontrado, conforme ilustra a Figura 2.

z	0,0	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199	0,5239	0,5279	0,5319	0,5359
0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596	0,5636	0,5675	0,5714	0,5753
0,2	0,5793	0,5832	0,5871	0,5910	0,5948	0,5987	0,6026	0,6064	0,6103	0,6141
0,3	0,6179	0,6217	0,6255	0,6293	0,6331	0,6368	0,6406	0,6443	0,6480	0,6517
0,4	0,6554	0,6591	0,6628	0,6664	0,6700	0,6736	0,6772	0,6808	0,6844	0,6879
0,5	0,6915	0,6950	0,6985	0,7019	0,7054	0,7088	0,7123	0,7157	0,7190	0,7224
0,6	0,7257	0,7291	0,7324	0,7357	0,7389	0,7422	0,7454	0,7486	0,7517	0,7549
0,7	0,7580	0,7611	0,7642	0,7673	0,7704	0,7734	0,7764	0,7794	0,7823	0,7852
0,8	0,7881	0,7910	0,7939	0,7967	0,7995	0,8023	0,8051	0,8078	0,8106	0,8133
0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289	0,8315	0,8340	0,8365	0,8389
1,0	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621
1,1	0,8643	0,8665	0,8686	0,8708	0,8729	0,8749	0,8770	0,8790	0,8810	0,8830
1,2	0,8849	0,8869	0,8888	0,8907	0,8925	0,8944	0,8962	0,8980	0,8997	0,9015
1,3	0,9032	0,9049	0,9066	0,9082	0,9099	0,9115	0,9131	0,9147	0,9162	0,9177
1,4	0,9192	0,9207	0,9222	0,9236	0,9251	0,9265	0,9279	0,9292	0,9306	0,9319
1,5	0,9332	0,9345	0,9357	0,9370	0,9382	0,9394	0,9406	0,9418	0,9429	0,9441
1,6	0,9452	0,9463	0,9474	0,9484	0,9495	0,9505	0,9515	0,9525	0,9535	0,9545
1,7	0,9554	0,9564	0,9573	0,9582	0,9591	0,9599	0,9608	0,9616	0,9625	0,9633
1,8	0,9641	0,9649	0,9656	0,9664	0,9671	0,9678	0,9686	0,9693	0,9699	0,9706
1,9	0,9713	0,9719	0,9726	0,9732	0,9738	0,9744	0,9750	0,9756	0,9761	0,9767
2,0	0,9772	0,9778	0,9783	0,9788	0,9793	0,9798	0,9803	0,9808	0,9812	0,9817
2,1	0,9821	0,9826	0,9830	0,9834	0,9838	0,9842	0,9846	0,9850	0,9854	0,9857
2,2	0,9861	0,9864	0,9868	0,9871	0,9875	0,9878	0,9881	0,9884	0,9887	0,9890
2,3	0,9893	0,9896	0,9898	0,9901	0,9904	0,9906	0,9909	0,9911	0,9913	0,9916
2,4	0,9918	0,9920	0,9922	0,9925	0,9927	0,9929	0,9931	0,9932	0,9934	0,9936
2,5	0,9938	0,9940	0,9941	0,9943	0,9945	0,9946	0,9948	0,9949	0,9951	0,9952
2,6	0,9953	0,9955	0,9956	0,9957	0,9959	0,9960	0,9961	0,9962	0,9963	0,9964
2,7	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972	0,9973	0,9974
2,8	0,9974	0,9975	0,9976	0,9977	0,9977	0,9978	0,9979	0,9979	0,9980	0,9981
2,9	0,9981	0,9982	0,9982	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986	0,9986
3,0	0,9987	0,9987	0,9987	0,9988	0,9988	0,9989	0,9989	0,9989	0,9990	0,9990
3,1	0,9990	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993
3,2	0,9993	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995
3,3	0,9995	0,9995	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997
3,4	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9998
3,5	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998
3,6	0,9998	0,9998	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
3,7	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
3,8	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
3,9	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000

Tabela 1 | Tabela da distribuição normal padrão acumulada (valores positivos do z-escore). Fonte: adaptada de Larson e Farber (2015).

 

z	0,0	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,5000	0,4960	0,4920	0,4880	0,4840	0,4801	0,4761	0,4721	0,4681	0,4641
-0,1	0,4602	0,4562	0,4522	0,4483	0,4443	0,4404	0,4364	0,4325	0,4286	0,4247
-0,2	0,4207	0,4168	0,4129	0,4090	0,4052	0,4013	0,3974	0,3936	0,3897	0,3859
-0,3	0,3821	0,3783	0,3745	0,3707	0,3669	0,3632	0,3594	0,3557	0,3520	0,3483
-0,4	0,3446	0,3409	0,3372	0,3336	0,3300	0,3264	0,3228	0,3192	0,3156	0,3121
-0,5	0,3085	0,3050	0,3015	0,2981	0,2946	0,2912	0,2877	0,2843	0,2810	0,2776
-0,6	0,2743	0,2709	0,2676	0,2643	0,2611	0,2578	0,2546	0,2514	0,2483	0,2451
-0,7	0,2420	0,2389	0,2358	0,2327	0,2296	0,2266	0,2236	0,2206	0,2177	0,2148
-0,8	0,2119	0,2090	0,2061	0,2033	0,2005	0,1977	0,1949	0,1922	0,1894	0,1867
-0,9	0,1841	0,1814	0,1788	0,1762	0,1736	0,1711	0,1685	0,1660	0,1635	0,1611
-1,0	0,1587	0,1562	0,1539	0,1515	0,1492	0,1469	0,1446	0,1423	0,1401	0,1379
-1,1	0,1357	0,1335	0,1314	0,1292	0,1271	0,1251	0,1230	0,1210	0,1190	0,1170
-1,2	0,1151	0,1131	0,1112	0,1093	0,1075	0,1056	0,1038	0,1020	0,1003	0,0985
-1,3	0,0968	0,0951	0,0934	0,0918	0,0901	0,0885	0,0869	0,0853	0,0838	0,0823
-1,4	0,0808	0,0793	0,0778	0,0764	0,0749	0,0735	0,0721	0,0708	0,0694	0,0681
-1,5	0,0668	0,0655	0,0643	0,0630	0,0618	0,0606	0,0594	0,0582	0,0571	0,0559
-1,6	0,0548	0,0537	0,0526	0,0516	0,0505	0,0495	0,0485	0,0475	0,0465	0,0455
-1,7	0,0446	0,0436	0,0427	0,0418	0,0409	0,0401	0,0392	0,0384	0,0375	0,0367
-1,8	0,0359	0,0351	0,0344	0,0336	0,0329	0,0322	0,0314	0,0307	0,0301	0,0294
-1,9	0,0287	0,0281	0,0274	0,0268	0,0262	0,0256	0,0250	0,0244	0,0239	0,0233
-2,0	0,0228	0,0222	0,0217	0,0212	0,0207	0,0202	0,0197	0,0192	0,0188	0,0183
-2,1	0,0179	0,0174	0,0170	0,0166	0,0162	0,0158	0,0154	0,0150	0,0146	0,0143
-2,2	0,0139	0,0136	0,0132	0,0129	0,0125	0,0122	0,0119	0,0116	0,0113	0,0110
-2,3	0,0107	0,0104	0,0102	0,0099	0,0096	0,0094	0,0091	0,0089	0,0087	0,0084
-2,4	0,0082	0,0080	0,0078	0,0075	0,0073	0,0071	0,0069	0,0068	0,0066	0,0064
-2,5	0,0062	0,0060	0,0059	0,0057	0,0055	0,0054	0,0052	0,0051	0,0049	0,0048
-2,6	0,0047	0,0045	0,0044	0,0043	0,0041	0,0040	0,0039	0,0038	0,0037	0,0036
-2,7	0,0035	0,0034	0,0033	0,0032	0,0031	0,0030	0,0029	0,0028	0,0027	0,0026
-2,8	0,0026	0,0025	0,0024	0,0023	0,0023	0,0022	0,0021	0,0021	0,0020	0,0019
-2,9	0,0019	0,0018	0,0018	0,0017	0,0016	0,0016	0,0015	0,0015	0,0014	0,0014
-3,0	0,0013	0,0013	0,0013	0,0012	0,0012	0,0011	0,0011	0,0011	0,0010	0,0010
-3,1	0,0010	0,0009	0,0009	0,0009	0,0008	0,0008	0,0008	0,0008	0,0007	0,0007
-3,2	0,0007	0,0007	0,0006	0,0006	0,0006	0,0006	0,0006	0,0005	0,0005	0,0005
-3,3	0,0005	0,0005	0,0005	0,0004	0,0004	0,0004	0,0004	0,0004	0,0004	0,0003
-3,4	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0002
-3,5	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002
-3,6	0,0002	0,0002	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001
-3,7	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001
-3,8	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001
-3,9	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000

Tabela 2 | Tabela da distribuição normal padrão acumulada (valores negativos do z-escore). Fonte: adaptada de Larson e Farber (2015).

 

Quando utilizamos essas tabelas para calcular a probabilidade, é importante observar que, se desejamos uma probabilidade maior do que o valor do z-escore, então devemos subtrair o valor encontrado na tabela da probabilidade total, ou seja, $P\left(Z\ge z\right)=1-P\left(P\le z\right).$

Siga em Frente...

Com base nos conceitos que discutimos até agora, vamos abordar um exemplo.

 

Exemplo

O tempo gasto no exame vestibular de certa universidade tem distribuição normal com média de 120 minutos e desvio-padrão de 15 minutos.

1. Qual é a probabilidade de que o tempo gasto seja menor que 90 minutos?
2. Qual é a probabilidade de que o tempo gasto seja maior que 130 minutos?

Para determinarmos a probabilidade de que o tempo gasto seja menor que 90 minutos, o primeiro passo é encontrar o z-escore.

$\mathit{z}=\frac{\mathit{x}-\mathit{\mu }}{\mathit{\sigma }}$

$z=\frac{90-120}{15}=-2$

Nesse sentido, temos que $P\left(X\le 90\right)=P(Z\le -2)$, conforme ilustra a Figura 3.

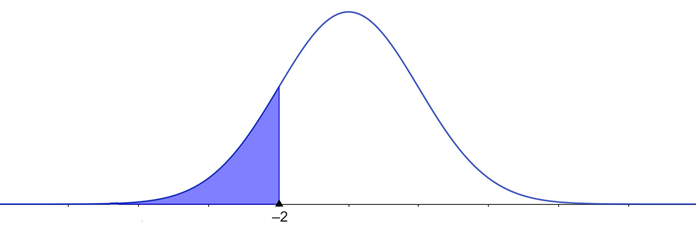
Utilizando a Tabela 2, encontre a área que corresponde $z=-2$ buscando -2,0 na coluna à esquerda e, depois, seguindo a linha até a coluna sob 0,0. O número naquela linha e coluna é 0,0228. Então, a área à esquerda de $z = -2$é 0,0228, conforme a Tabela 3.

z	0,0	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,5000	0,4960	0,4920	0,4880	0,4840	0,4801	0,4761	0,4721	0,4681	0,4641
-0,1	0,4602	0,4562	0,4522	0,4483	0,4443	0,4404	0,4364	0,4325	0,4286	0,4247
-0,2	0,4207	0,4168	0,4129	0,4090	0,4052	0,4013	0,3974	0,3936	0,3897	0,3859
-0,3	0,3821	0,3783	0,3745	0,3707	0,3669	0,3632	0,3594	0,3557	0,3520	0,3483
-0,4	0,3446	0,3409	0,3372	0,3336	0,3300	0,3264	0,3228	0,3192	0,3156	0,3121
-0,5	0,3085	0,3050	0,3015	0,2981	0,2946	0,2912	0,2877	0,2843	0,2810	0,2776
-0,6	0,2743	0,2709	0,2676	0,2643	0,2611	0,2578	0,2546	0,2514	0,2483	0,2451
-0,7	0,2420	0,2389	0,2358	0,2327	0,2296	0,2266	0,2236	0,2206	0,2177	0,2148
-0,8	0,2119	0,2090	0,2061	0,2033	0,2005	0,1977	0,1949	0,1922	0,1894	0,1867
-0,9	0,1841	0,1814	0,1788	0,1762	0,1736	0,1711	0,1685	0,1660	0,1635	0,1611
-1,0	0,1587	0,1562	0,1539	0,1515	0,1492	0,1469	0,1446	0,1423	0,1401	0,1379
-1,1	0,1357	0,1335	0,1314	0,1292	0,1271	0,1251	0,1230	0,1210	0,1190	0,1170
-1,2	0,1151	0,1131	0,1112	0,1093	0,1075	0,1056	0,1038	0,1020	0,1003	0,0985
-1,3	0,0968	0,0951	0,0934	0,0918	0,0901	0,0885	0,0869	0,0853	0,0838	0,0823
-1,4	0,0808	0,0793	0,0778	0,0764	0,0749	0,0735	0,0721	0,0708	0,0694	0,0681
-1,5	0,0668	0,0655	0,0643	0,0630	0,0618	0,0606	0,0594	0,0582	0,0571	0,0559
-1,6	0,0548	0,0537	0,0526	0,0516	0,0505	0,0495	0,0485	0,0475	0,0465	0,0455
-1,7	0,0446	0,0436	0,0427	0,0418	0,0409	0,0401	0,0392	0,0384	0,0375	0,0367
-1,8	0,0359	0,0351	0,0344	0,0336	0,0329	0,0322	0,0314	0,0307	0,0301	0,0294
-1,9	0,0287	0,0281	0,0274	0,0268	0,0262	0,0256	0,0250	0,0244	0,0239	0,0233
-2,0	0,0228	0,0222	0,0217	0,0212	0,0207	0,0202	0,0197	0,0192	0,0188	0,0183
-2,1	0,0179	0,0174	0,0170	0,0166	0,0162	0,0158	0,0154	0,0150	0,0146	0,0143
-2,2	0,0139	0,0136	0,0132	0,0129	0,0125	0,0122	0,0119	0,0116	0,0113	0,0110
-2,3	0,0107	0,0104	0,0102	0,0099	0,0096	0,0094	0,0091	0,0089	0,0087	0,0084

Tabela 3 | z-escore para z ≤ -2. Fonte: elaborada pela autora.

 

Portanto, a probabilidade de que o tempo gasto seja menor que 90 minutos é 0,0228, ou seja, 2,28%.

Agora vamos determinar a probabilidade de que o tempo gasto seja maior que 130 minutos. O z-escore será:

$\mathit{z}=\frac{\mathit{x}-\mathit{\mu }}{\mathit{\sigma }}$

$z=\frac{130-120}{15}=\mathrm{0,67}$

Nesse sentido, temos que $P\left(X\ge 130\right)=P(Z\ge \mathrm{0,67})$, conforme ilustra a Figura 4.

Utilizando a Tabela 1, encontre a área que corresponde $z=\mathrm{0,67}$ buscando 0,6 na coluna à esquerda e, depois, seguindo a linha até a coluna sob 0,07. O número naquela linha e coluna é 0,7486. Então, a área à esquerda de $z = \mathrm{0,67}$ é 0,7486, conforme a Tabela 4.

z	0,0	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199	0,5239	0,5279	0,5319	0,5359
0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596	0,5636	0,5675	0,5714	0,5753
0,2	0,5793	0,5832	0,5871	0,5910	0,5948	0,5987	0,6026	0,6064	0,6103	0,6141
0,3	0,6179	0,6217	0,6255	0,6293	0,6331	0,6368	0,6406	0,6443	0,6480	0,6517
0,4	0,6554	0,6591	0,6628	0,6664	0,6700	0,6736	0,6772	0,6808	0,6844	0,6879
0,5	0,6915	0,6950	0,6985	0,7019	0,7054	0,7088	0,7123	0,7157	0,7190	0,7224
0,6	0,7257	0,7291	0,7324	0,7357	0,7389	0,7422	0,7454	0,7486	0,7517	0,7549
0,7	0,7580	0,7611	0,7642	0,7673	0,7704	0,7734	0,7764	0,7794	0,7823	0,7852
0,8	0,7881	0,7910	0,7939	0,7967	0,7995	0,8023	0,8051	0,8078	0,8106	0,8133
0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289	0,8315	0,8340	0,8365	0,8389
1,0	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621
1,1	0,8643	0,8665	0,8686	0,8708	0,8729	0,8749	0,8770	0,8790	0,8810	0,8830

Tabela 4 | z-escore para z ≤ 0,67. Fonte: elaborada pela autora.

 

Essa não é a probabilidade que queremos. Queremos a área à direita de $z=\mathrm{0,67}$ então temos que diminuir o valor encontrado de 1:

$P\left(Z\ge \mathrm{0,67}\right)=1-P\left(Z\le \mathrm{0,67}\right)=1-\mathrm{0,7486}=\mathrm{0,2514}$

Logo, a probabilidade de que o tempo gasto seja maior que 130 minutos é 0,2514, ou seja, 25,14%.

Vale destacar que existem várias tabelas disponíveis, e, ao resolver um problema de distribuição normal, é crucial estar ciente de qual tabela está sendo utilizada. Uma interpretação equivocada da tabela pode resultar em erros na resolução do problema.

Vamos Exercitar?

Agora que você já conheceu os princípios relacionados à distribuição de probabilidade normal padronizada, vamos retomar nossa situação inicial. Nessa situação, certa empresa de celulares fez um estudo a respeito da vida útil das baterias dos celulares e constatou que elas têm uma duração com distribuição normal com média de 8 horas e desvio-padrão de 2 horas. Com base nessas informações, temos que determinar algumas probabilidades:

a) Para determinarmos a probabilidade de a bateria durar menos que 7 horas, primeiro devemos encontrar o z-escore:

$\mathit{z}=\frac{\mathit{x}-\mathit{\mu }}{\mathit{\sigma }}$

$z=\frac{7-8}{2}=-\mathrm{0,5}$

Nesse sentido, temos que $P\left(X\le 7\right)=P(Z\le -\mathrm{0,5})$, conforme ilustra a Figura 5.

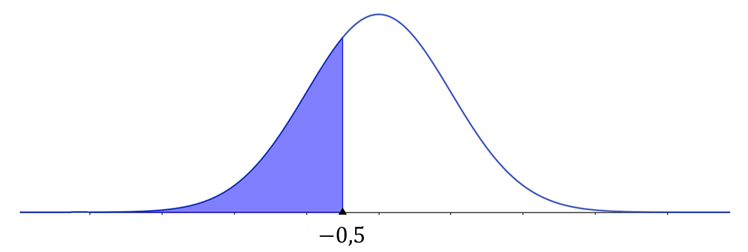
Utilizando a Tabela 2, encontre a área que corresponde $z=-\mathrm{0,5}$ buscando -0,5 na coluna à esquerda e, depois, seguindo a linha até a coluna sob 0,0. O número naquela linha e coluna é 0,3085. Então, a área à esquerda de $z = -\mathrm{0,5}$ é 0,3085, conforme a Tabela 5.

z	0,0	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,5000	0,4960	0,4920	0,4880	0,4840	0,4801	0,4761	0,4721	0,4681	0,4641
-0,1	0,4602	0,4562	0,4522	0,4483	0,4443	0,4404	0,4364	0,4325	0,4286	0,4247
-0,2	0,4207	0,4168	0,4129	0,4090	0,4052	0,4013	0,3974	0,3936	0,3897	0,3859
-0,3	0,3821	0,3783	0,3745	0,3707	0,3669	0,3632	0,3594	0,3557	0,3520	0,3483
-0,4	0,3446	0,3409	0,3372	0,3336	0,3300	0,3264	0,3228	0,3192	0,3156	0,3121
-0,5	0,3085	0,3050	0,3015	0,2981	0,2946	0,2912	0,2877	0,2843	0,2810	0,2776
-0,6	0,2743	0,2709	0,2676	0,2643	0,2611	0,2578	0,2546	0,2514	0,2483	0,2451

Tabela 5 | z-escore para z ≤ -0,5. Fonte: elaborada pela autora.

 

Portanto, a probabilidade de que a bateria dure menos que 7 horas é de $\mathrm{0,3085}$ ou seja, 30,85%.

Caso você não tenha acesso à tabela com valores negativos do z-escore, você pode utilizar o fato de que a curva normal é simétrica. Assim, a probabilidade de z ser menor que -0,5 é a mesma de que z seja maior que 0,5, ou seja $P\left(Z\le -\mathrm{0,5}\right)=P\left(Z\ge \mathrm{0,5}\right)=1-P\left(Z\le \mathrm{0,5}\right)=1-\mathrm{0,6915}=\mathrm{0,3085}$.

b) Como já encontramos o z-escore considerando a duração da bateria de 7 horas, só precisamos interpretar o problema. Foi solicitado que determinemos a probabilidade de a bateria durar mais que 7 horas, ou seja $P\left(Z\ge -\mathrm{0,5}\right)=1-P\left(Z\le -\mathrm{0,5}\right)=1-\mathrm{0,3085}=\mathrm{0,6915}$. Portanto, a probabilidade de que a bateria dure mais que 7 horas é de 69,15%.

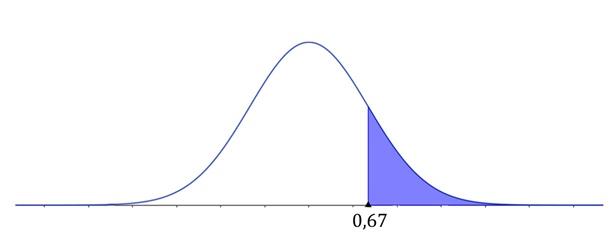
c) Para calcular a probabilidade de que a bateria dure entre 7 e 10 horas, inicialmente devemos calcular os z-escores associados aos valores 7 e 10. Como já sabemos o z-escore relacionado a 7, vamos calcular o z-escore de 10.

$\mathit{z}=\frac{\mathit{x}-\mathit{\mu }}{\mathit{\sigma }}$

$z=\frac{10-8}{2}=1$

 

Nesse sentido, temos que $P\left(7\le X\le 10\right)=P(-\mathrm{0,5}\le Z\le 1)$, conforme ilustra a Figura 6.

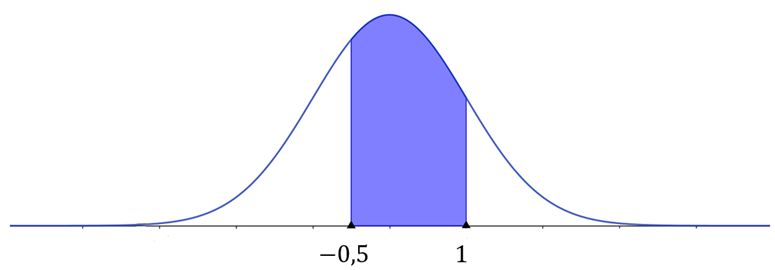
Observe que, para determinarmos a área da região colorida, primeiro devemos encontrar a área correspondente a cada z-escore nas tabelas e, depois, realizar uma subtração entre a área maior e a área menor. Portanto,

$P\left(7\le X\le 10\right)=P\left(-\mathrm{0,5}\le Z\le 1\right)=P\left(Z\le 1\right)-P\left(Z\le -,05\right)=\mathrm{0,8413}-\mathrm{0,3085}=\mathrm{0,5328}$

Assim, a probabilidade de que a bateria dure entre 7 e 10 horas é de $0,5328$, isto é, de 53,28%. 

Saiba Mais

Uma estratégia fundamental de aprendizado em matemática envolve a resolução de exercícios, pois essa abordagem permite a aplicação das diversas propriedades ligadas aos conteúdos discutidos. Portanto, recomendamos a leitura e a realização de alguns exercícios com os temas abordados durante a aula. 
Com o objetivo de aprimorar seus conhecimentos sobre a distribuição normal padronizada, sugerimos que leia as seções 5.1 e 5.2 do livro Estatística aplicada. Após concluir a leitura do capítulo, escolha alguns exercícios para resolver!

Referências Bibliográficas

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023. 

Métodos quantitativos

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Chegada

Olá, estudante!

Para desenvolver a competência desta unidade, que é compreender os princípios básicos da probabilidade e identificar as características dos diferentes tipos de distribuição de probabilidade, você precisa saber reconhecer quais são esses princípios.

A probabilidade é uma medida numérica que descreve a chance de um evento acontecer. Ela é usada para quantificar a incerteza em situações em que múltiplos resultados possíveis são possíveis. A probabilidade é expressa como um número entre 0 e 1, onde 0 indica a certeza de que um evento não ocorrerá, e 1 indica a certeza de que um evento ocorrerá. A probabilidade de que um evento A ocorra será dada por:

$P\left(A\right)=\frac{\mathrm{número}\mathrm{ }\mathrm{de}\mathrm{ }\mathrm{resultado}\mathrm{ }\mathrm{do}\mathrm{ }\mathrm{evento}\mathrm{ }\mathrm{A}}{\mathrm{número}\mathrm{ }\mathrm{total}\mathrm{ }\mathrm{de}\mathrm{ }\mathrm{resultados}\mathrm{ }\mathrm{do}\mathrm{ }\mathrm{espaço}\mathrm{ }\mathrm{amostral}}=\frac{n\left(A\right)}{n\left(\mathrm{\Omega }\right)}$

 

Normalmente empregamos porcentagem para representar probabilidades, de modo que, após efetuar o cálculo, é suficiente multiplicar o valor obtido por 100 para obter a probabilidade em forma percentual.

Um conceito fundamental é o da probabilidade condicional, que consiste em uma medida de probabilidade com enfoque na ocorrência de um evento, levando em consideração que outro evento já aconteceu. Em termos simples, ela representa a probabilidade de um evento A acontecer, levando em consideração que um evento B já se concretizou. A probabilidade condicional desempenha um papel crucial na estatística e na teoria da probabilidade, sendo aplicada em diversas áreas, tais como análise de risco, inferência estatística, tomada de decisões e modelagem estatística. Ela permite que avaliemos a probabilidade de um evento com base em informações anteriores ou condicionantes, tornando-se uma ferramenta valiosa para lidar com cenários de incerteza.

É importante lembrar que uma variável aleatória pode ser categorizada como discreta quando seus valores possíveis formam um conjunto finito ou contável. Por outro lado, ela será considerada contínua quando abranger um conjunto infinito e incontável de valores em um intervalo contínuo. Saber diferenciar o tipo de variável aleatória que o problema trata é fundamental para nos direcionar ao tipo de distribuição de probabilidade que podemos utilizar. Na distribuição de probabilidade, as probabilidades associadas a diferentes resultados em um espaço amostral são transformadas em probabilidades específicas relacionadas aos valores individuais da variável aleatória $X$. A distribuição de probabilidade de $X$ descreve como a probabilidade total de 1 se distribui entre os diversos valores potenciais de $X$.

A distribuição binomial é uma distribuição discreta de probabilidade que apresenta as seguintes características:

• Cada tentativa ou ensaio é considerado independente, com apenas dois resultados possíveis: sucesso (S) e fracasso (F).
• Pressupõe um número fixo de tentativas ou ensaios, geralmente denotado como .
• A probabilidade de sucesso em cada tentativa é constante e denotada como 
• Cada tentativa é independente das outras, o que significa que o resultado de uma tentativa não afeta o resultado das tentativas subsequentes.
• A variável aleatória associada à distribuição binomial é o número de sucessos  em  tentativas.
• A probabilidade binomial é dada por:

$\mathit{P}\left(\mathit{x}\right)=\mathit{P}\left(\mathit{X}=\mathit{x}\right)={\mathit{C}}_{\mathit{n}}^{\mathit{x}}\cdot {\mathit{p}}^{\mathit{x}}\cdot {\mathit{q}}^{\mathit{n}-\mathit{x}}$

A distribuição de Poisson também é uma distribuição discreta e apresenta as seguintes características:

• É aplicada a situações em que os eventos ocorrem em um contexto discreto.
• Assume que os eventos são independentes uns dos outros, o que significa que a ocorrência de um evento não afeta a probabilidade de ocorrência de outros eventos.
• É definida por um único parâmetro, $\lambda$ (lambda), que representa a taxa média de ocorrência dos eventos no intervalo considerado.
• A probabilidade será dada por:

$\mathit{P}\left(\mathit{x}\right)=\mathit{P}\left(\mathit{X}=\mathit{x}\right)=\frac{{\mathit{e}}^{-\mathit{\lambda }}\cdot {\mathit{\lambda }}^{\mathit{x}}}{\mathit{x}!}$

A distribuição normal padronizada é uma distribuição contínua de probabilidade e tem papel fundamental na estatística inferencial. São características dessa distribuição:

• É contínua e abrange todos os números reais de menos infinito a mais infinito. Não há valores específicos de $x$ que sejam impossíveis na distribuição normal.
• Tem uma forma de sino, com uma curva simétrica em relação a seu ponto médio. Isso significa que a maioria dos valores está próxima da média, e os valores extremos são menos frequentes.
• A distribuição normal é completamente caracterizada por dois parâmetros: a média $\left(\mu \right)$ e o desvio-padrão $\left(\sigma \right)$. A média determina o centro da distribuição, enquanto o desvio-padrão controla a dispersão dos valores em relação à média.
• A distribuição normal padronizada tem média zero e desvio padrão 1, e a representamos como $N\left(\mathrm{0,1}\right)$.
• Para padronizarmos nossa variável aleatória, é necessário determinar o z-escore, dado por:

$\mathit{z}=\frac{\mathit{x}-\mathit{\mu }}{\mathit{\sigma }}$

• A probabilidade será definida ao encontrar a área referente ao z-escore. Para isso, utilizamos uma tabela de distribuição normal acumulada.

Compreender esses conceitos é muito importante, uma vez que eles desempenham um papel fundamental na probabilidade e na estatística inferencial.

É Hora de Praticar!

Para contextualizar sua aprendizagem, suponha que você esteja participando de um processo seletivo para ingressar em um programa de iniciação científica. Esse programa tem como objetivo estudar o papel da estatística no campo profissional. A primeira parte do processo seletivo consiste em uma prova de conhecimentos gerais, que englobam os conceitos relacionados às diferentes disciplinas de seu curso. Com o objetivo de se preparar para essa primeira etapa, você decidiu realizar uma pesquisa sobre os conceitos mais recorrentes nas provas anteriores. Como resultado, constatou que conceitos relacionados à probabilidade eram recorrentes em todas as provas. Após analisar as provas, você selecionou algumas questões com o objetivo de realizar um simulado para essa primeira etapa do processo seletivo. Sua tarefa, então, é resolver as questões que compõem esse simulado, conforme apresentado a seguir.

 

Questão 1

Com o objetivo de avaliar a eficácia de um medicamento específico na redução dos níveis de colesterol na corrente sanguínea, conduziu-se um ensaio clínico envolvendo 100 participantes que passaram a utilizar esse medicamento. Após a conclusão do teste, observou-se que os dados se distribuem normalmente e que a média de colesterol desses indivíduos foi de 120 mg/dl, com um desvio-padrão de 4 mg/dl. Qual é a probabilidade de que uma pessoa tenha o colesterol superior a 125 mg/dl?

 

Questão 2

Considera-se que 30% dos residentes nas proximidades de uma extensa indústria siderúrgica são afetados por alergias devido aos poluentes liberados na atmosfera. Supondo que essa taxa de alergia seja precisa (verídica), qual é a probabilidade de que, ao selecionar 10 moradores ao acaso, pelo menos 3 tenham alergia?

 

Questão 3

Uma estação de rádio recebe, em média, 15 pedidos de músicas clássicas por hora. Qual é a probabilidade de receber exatamente 5 pedidos de músicas clássicas em um período de 30 minutos?

Reflita

Considerando a ampla variedade de situações em que os conceitos abordados na unidade podem ser aplicados, convidamos à reflexão sobre estas duas questões:

1. De que maneira os conceitos relacionados à probabilidade podem ser utilizados em sua área de atuação?
2. De que forma os conceitos probabilísticos podem auxiliar na tomada de decisão? 

Resolução do estudo de caso

Solução da questão 1

Observe que, nesse problema, os dados são distribuídos normalmente e sabemos dois parâmetros: a média de 120 mg/dl e o desvio-padrão de 4 mg/dl. Para determinarmos a probabilidade de que uma pessoa tenha o colesterol superior a 125 mg/dl, vamos utilizar a distribuição normal padrão. O primeiro passo é determinarmos o z-escore:

$\mathit{z}=\frac{\mathit{x}-\mathit{\mu }}{\mathit{\sigma }}$

$z=\frac{125-120}{4}=\mathrm{1,25}$

Nesse sentido, temos que $P\left(X\ge 1250\right)=P(Z\ge \mathrm{1,25})$, conforme a Figura 1.

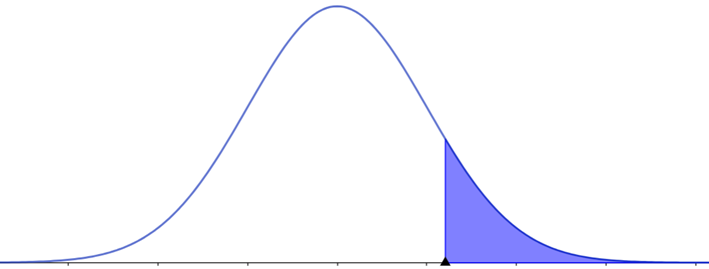
Utilizando a uma tabela da distribuição normal padrão acumulada, encontraremos a área que corresponde $z=1,25$buscando 1,2 na coluna à esquerda e, depois, seguindo a linha até a coluna sob 0,05. O número naquela linha e coluna é 0,8944. Então, a área à esquerda de $z = 1,25$0,8944 (Tabela 1).

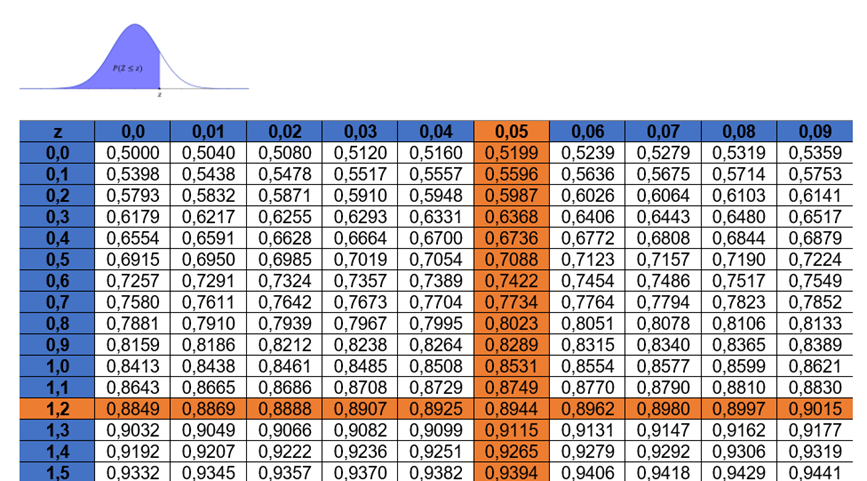
Essa não é a probabilidade que queremos. Queremos a área à direita de $z=\mathrm{1,25}$, então temos que diminuir o valor encontrado de 1:

$P\left(Z\ge \mathrm{01,25}\right)=1-P\left(Z\le \mathrm{1,25}\right)=1-\mathrm{0,8944}=\mathrm{0,1056}$

Logo, a probabilidade de que uma pessoa tenha o colesterol superior a 125 mg/dl é de 0,1056, ou seja, 10,56%.

 

Solução da questão 2

No problema foi informado que 30% dos residentes nas proximidades de uma extensa indústria siderúrgica são afetados por alergias. Devemos determinar a probabilidade de que, ao selecionar 10 moradores ao acaso, pelo menos 3 tenham alergia.

Podemos utilizar a distribuição binomial, uma vez que só temos dois resultados possíveis: ou a pessoa tem alergia ou não tem. Além disso, foi selecionado um número fixo de pessoas. É importante destacar que a questão requer a probabilidade de que pelo menos 3 moradores tenham alergia, então precisamos calcular a probabilidade de que 3, 4, …, 10 moradores tenham alergia e depois somá-la. Mas perceba que teríamos que fazer muitos cálculos. Esse problema pode ser abordado considerando-se o princípio de que a soma total das probabilidades é igual a 1. Se desejamos calcular a probabilidade de que pelo menos 3 pessoas tenham alergia, isso significa que não estamos interessados na probabilidade de que nenhuma pessoa tenha alergia ou de que apenas uma pessoa tenha ou de que duas pessoas tenham alergia. Subtraindo a soma das probabilidades de não ter alergia, de ter 1 pessoa com alergia e ter 2 pessoas com alergia de 1, obteremos a probabilidade de que pelo menos 3 pessoas tenham alergia, ou seja, $P\left(X\ge 2\right)=1-[P\left(X=0\right)+P\left(X=1\right)+P(X=2\left)\right]$. Vamos calcular essas probabilidades:

$P\left(x\right)=P(X=x)=C_n^x\cdot p^x\cdot q^{n-x} \left\{\begin{array}{c}p=30\%=\mathrm{0,3} \\ q=1-p=1-\mathrm{0,3}=\mathrm{0,7}\end{array}\right.$

$P\left(0\right)=P\left(X=0\right)=C_{10}^0\cdot {\left(\mathrm{0,3}\right)}^0\cdot {\left(\mathrm{0,7}\right)}^{10-0}=\frac{10!}{0!\left(10-0\right)!}\cdot {\left(\mathrm{0,3}\right)}^0\cdot {\left(\mathrm{0,7}\right)}^{10}\approx \mathrm{0,028}$

$P\left(1\right)=P\left(X=1\right)=C_{10}^1\cdot {\left(\mathrm{0,3}\right)}^1\cdot {\left(\mathrm{0,7}\right)}^{10-1}=\frac{10!}{1!\left(10-1\right)!}\cdot {\left(\mathrm{0,3}\right)}^1\cdot {\left(\mathrm{0,7}\right)}^9\approx \mathrm{0,121}$

$P\left(2\right)=P\left(X=2\right)=C_{10}^2\cdot {\left(\mathrm{0,3}\right)}^2\cdot {\left(\mathrm{0,7}\right)}^{10-2}=\frac{10!}{2!\left(10-2\right)!}\cdot {\left(\mathrm{0,3}\right)}^2\cdot {\left(\mathrm{0,7}\right)}^8\approx \mathrm{0,233}$

$P\left(X\ge 2\right)=1-\left[\mathrm{0,028}+\mathrm{0,121}+\mathrm{0,233}\right]=1-\mathrm{0,382}\approx \mathrm{0,618}$

Portanto, a probabilidade de que, ao selecionar 10 moradores ao acaso, pelo menos 3 moradores tenham alergia é de aproximadamente 61,8%.

 

Solução da questão 3

Inicialmente, é necessário determinar a média de pedidos de músicas por unidade de referência, que, nesse caso, é de 15 pedidos de músicas clássicas por hora. O problema busca a probabilidade de receber exatamente 5 pedidos de músicas clássicas em um período de 30 minutos; observe que o intervalo de referência difere da informação inicial do problema. Para encontrar o número de pedidos no novo intervalo, podemos empregar uma regra de três:

$15 pedidos---------1 hora$

$z pedidos--------\mathrm{0,5} hora$

$z\cdot 1=\mathrm{0,5}\cdot 15$

$z=\mathrm{7,5} pedidos$

Portanto, $\lambda =\mathrm{7,5}$. Agora vamos calcular a probabilidade de que sejam pedidas exatamente 5 músicas:

$P\left(x\right)=P\left(X=x\right)=\frac{e^{-\lambda }\cdot {\lambda }^x}{x!}$

$P\left(5\right)=P\left(X=5\right)=\frac{e^{-\mathrm{7,5}}\cdot {\left(\mathrm{7,5}\right)}^5}{5!}\approx \mathrm{0,109}$

Portanto, a probabilidade de a rádio receber exatamente 5 pedidos de músicas clássicas em um período de 30 minutos é de aproximadamente 10,9%.

Dê o play!

Assimile

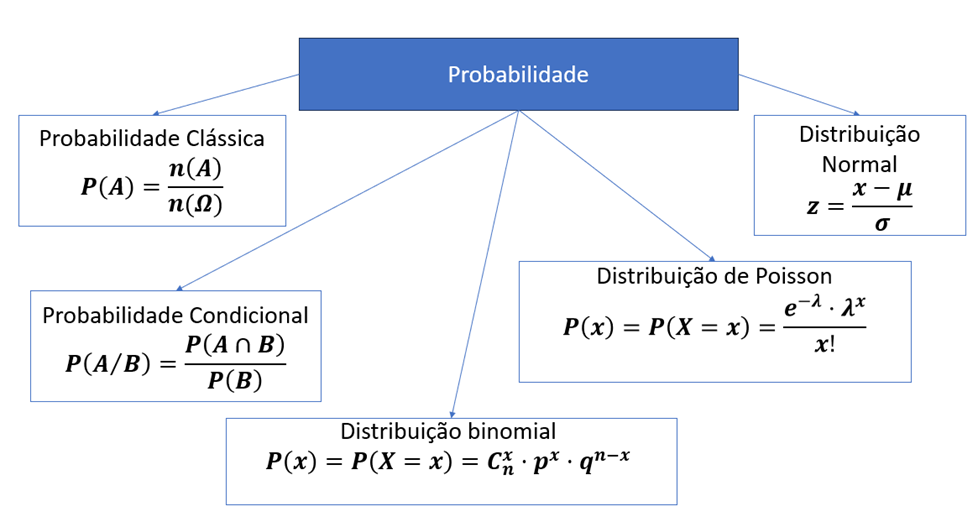
Ao se aventurar no campo da probabilidade, é fundamental ter o conhecimento dos variados métodos disponíveis para abordar problemas, escolhendo aquele mais adequado de acordo com as características específicas de cada situação. A Figura 2 ilustra os principais conceitos da probabilidade.

Referências

COSTA NETO, P. L. de O. Estatística. São Paulo: Blucher, 2006. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521215226/ . Acesso em: 24 out. 2023.

CRESPO, A. A. Estatística fácil. São Paulo: Saraiva, 2009. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788502122345/ . Acesso em: 24 out. 2023.

DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo: Cengage Learning, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128044/ . Acesso em: 24 out. 2023.

LARSON, R.; FARBER, B. Estatística aplicada. 6. ed. São Paulo: Pearson, 2015. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 24 out. 2023.

SILVA, E. M. da et al. Estatística. 5. ed. São Paulo: Atlas, 2018. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788597014273/. Acesso em: 24 out. 2023.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788547214753/ . Acesso em: 1º nov. 2023.