Dinâmica - Leis de Newton do Movimento e suas Aplicações

Leis de Newton

Olá, estudante! Nesta videoaula, você conhecerá as leis de Newton. As leis de Newton, formuladas por Sir Isaac Newton no século XVII, são princípios fundamentais da mecânica clássica que descrevem o movimento de objetos e as forças que atuam sobre eles. Elas são essenciais para entender o comportamento de corpos em movimento e estão entre as bases da física clássica.

Esse conteúdo é importante para a sua prática profissional, pois essas leis formam a base para compreender uma ampla variedade de fenômenos físicos, desde o movimento de planetas até o funcionamento de máquinas e veículos.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Olá, estudante! Seja bem-vindo.

A mecânica é uma área fundamental da física que estuda o movimento e o comportamento dos corpos físicos sob a influência de forças. Ela está dividida em duas partes principais: a cinemática e a dinâmica. A cinemática é responsável pela descrição do movimento, sem considerar as causas que o geram. Isso inclui conceitos, como posição, velocidade e aceleração. Já a dinâmica está preocupada com as forças que causam movimento e como elas estão relacionadas ao movimento dos corpos. As leis de Newton são fundamentais para a compreensão da dinâmica. A dinâmica é essencial para entender e prever o movimento dos corpos e para diversas áreas, incluindo engenharia, astronomia, biologia e muitas outras disciplinas científicas.

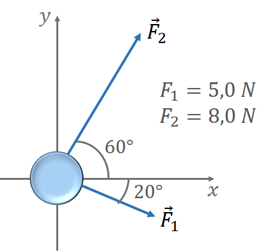
Para ilustrar os novos conhecimentos, consideraremos a seguinte situação-problema: um disco de hóquei com massa de 0,30 kg desliza sobre a superfície horizontal sem atrito de uma pista de gelo. Dois bastões de hóquei batem no disco ao mesmo tempo, exercendo forças sobre ele, como mostra a Figura 1. A força ${\overrightarrow{F}}_1$ tem módulo de 5,0 N e é dirigida a $\theta$ = 20° abaixo do eixo $x$. A força ${\overrightarrow{F}}_2$ tem módulo de 8,0 N e sua direção é $\varphi$ = 60° acima do eixo $x$. Determine o módulo da aceleração do disco.

Aproveite ao máximo as etapas que serão apresentadas a você, assumindo um compromisso especial com os estudos propostos. Encare o estudo como algo prazeroso, que lhe trará apenas enriquecimentos.

Vamos começar? Bons estudos!

Vamos Começar!

Uma das bases daquilo que chamamos de mecânica clássica são as três leis de Newton, apresentadas como princípios no livro Philosophiae Naturalis Principia Mathematica, comumente conhecido por Principia, escrito pelo físico e matemático Isaac Newton (1643-1727). Esses escritos estabelecem uma estrutura básica para se estudar o movimento dos corpos, especialmente no que diz respeito à causa de um movimento. O ramo da mecânica que engloba esses conhecimentos denomina-se dinâmica.

Primeira lei de Newton

A primeira lei de Newton também é conhecida como lei da inércia e indica que:

“Todo corpo permanece em estado de repouso, ou de movimento uniforme em linha reta, a menos que seja compelido a mudar esse estado de movimento em virtude de forças exercidas sobre ele” (Keller; Gettys; Skove, 1997, p. 99).

Então, a única forma de alterar o estado de movimento de um objeto é se alguma grandeza física provocar isso. A essa grandeza física vetorial damos o nome de força $\overrightarrow{F}$. A força pode ser traduzida na prática como o empurrão ou puxão que damos nos objetos, que tem sempre uma direção e um sentido, além de uma intensidade, mas precisamos ter um cuidado: nem sempre é necessário o contato direto entre dois corpos para que atue uma força.

A primeira lei de Newton também é chamada de lei da inércia em alguns livros, pois a propriedade da inércia está relacionada com a dificuldade ou facilidade de um corpo em ter seu vetor velocidade alterado. A medida numérica relacionada ao conceito da inércia é o que chamamos de massa ($\mathit{m}$). Assim, um objeto de maior massa oferece mais resistência ao entrar em movimento ou voltar para o estado de repouso.

Entretanto, só podemos dizer que um objeto está em um estado de inércia se podemos especificar o referencial para o qual sua velocidade é constante. Imaginaremos uma situação em que a pessoa 1 está dentro de um ônibus que viaja com velocidade $\overrightarrow{v}$ constante, observando a pessoa 2 na calçada. No referencial da pessoa 1, o ônibus está em repouso e a pessoa 2 está em movimento, enquanto no referencial da pessoa 2, o ônibus e a pessoa 1 estão em movimento. Note que ambas estão corretas no que diz respeito ao seu próprio referencial.

As leis de Newton são válidas para referenciais inerciais, o que quer dizer referenciais que não estão sofrendo uma aceleração.

Outra maneira de enunciar a primeira lei de Newton é a seguinte:

“Na ausência de forças externas e quando visualizado a partir de um referencial inercial, um corpo em repouso permanece em repouso e um corpo em movimento continua em movimento com uma velocidade constante (isto é, com velocidade constante em linha reta)” (Serway; Jewett, 2017, p. 109).

Em outras palavras, quando nenhuma força age sobre um corpo, a aceleração do objeto é zero. Da primeira lei, concluímos que qualquer corpo isolado (que não interage com seu ambiente) ou está em repouso, ou em movimento com velocidade constante. A tendência de um corpo de resistir a qualquer tentativa de mudança de sua velocidade é chamada inércia.

Dado o enunciado da primeira lei, podemos concluir que um corpo que está acelerando deve estar sofrendo uma força. Por sua vez, pela primeira lei, podemos definir força como o que causa uma mudança no movimento de um corpo.

Segunda lei de Newton

A primeira lei de Newton explica o que acontece com um corpo quando nenhuma força age sobre ele: mantém seu movimento original, ou permanece em repouso, ou move-se em linha reta com velocidade constante. Também, temos como resultado imediato que a força $\overrightarrow{F}$ agindo no objeto alterará seu estado de movimento, com o surgimento de uma aceleração $\overrightarrow{a}$. A segunda lei oferece uma forma de relacionar essas duas grandezas:

“Quando uma força resultante externa atua sobre um corpo, ele se acelera. A aceleração possui a mesma direção e sentido da força resultante. O vetor força resultante é igual ao produto da massa do corpo pelo vetor aceleração do corpo” (Young; Freedman, 2016, p. 119).

Em linguagem matemática, a segunda lei de Newton pode ser escrita como: ${\overrightarrow{F}}_R=m\overrightarrow{a}$, em que $m$ representa a massa do corpo, e o vetor ${\overrightarrow{F}}_R$ é a força resultante atuante no sistema. A força resultante é a soma vetorial de todas as forças atuando no corpo em um determinado instante:

${\overrightarrow{F}}_R={\overrightarrow{F}}_1+{\overrightarrow{F}}_2+{\overrightarrow{F}}_3+\dots =\sum _n{\overrightarrow{F}}_n$

Nos casos em que é necessário somar forças em diferentes direções, podemos utilizar o princípio de independência de Galileu para obter as componentes do vetor aceleração separadamente:

${\overrightarrow{F}}_x=m{\overrightarrow{a}}_x {\overrightarrow{F}}_y=m{\overrightarrow{a}}_y {\overrightarrow{F}}_z=m{\overrightarrow{a}}_z$

A unidade de força pode ser obtida pela análise dimensional da equação apresentada, lembrando que a unidade padrão de massa é o quilograma ($kg$) e de aceleração é metro por segundo ao quadrado ($m/s^2$). Essa combinação de unidades fundamentais do SI foi chamada de Newton ($N$).

Exemplo: para empurrar uma caixa muito pesada de $150 kg$, duas pessoas aplicam as forças ${\overrightarrow{F}}_1=15 N \hat{i} e {\overrightarrow{F}}_2=10 N \hat{i}$. Como resistência de contato entre o solo e a caixa, há uma força contrária (mesma direção e sentido contrário) de módulo $5 N$. Com essas informações, responda:

(a) Qual será o módulo e a orientação do vetor força resultante?

(b) E do vetor aceleração?

Resolução:

(a) A soma vetorial das forças resulta em:

${\overrightarrow{F}}_R={\overrightarrow{F}}_1+{\overrightarrow{F}}_2+{\overrightarrow{F}}_3$

${\overrightarrow{F}}_R=15\hat{i}+10\hat{i}-5\hat{i}$

${\overrightarrow{F}}_R=20 N \hat{i}$

A força resultante está orientada na direção horizontal, da esquerda para a direita.

(b) Com o valor do módulo força resultante obtido no item (a), podemos aplicar a segunda lei de Newton para obter o valor do módulo da aceleração:

${|\overrightarrow{F}}_R\left|=m\right|\overrightarrow{a}| \to \left|\overrightarrow{a}\right|=\frac{\left|{\overrightarrow{F}}_R\right|}{m}$

Substituindo os valores numéricos, temos que:

$\left|\overrightarrow{a}\right|=\frac{20}{150}=\mathrm{0,16} m/s^2$

De acordo com a lei de Newton, a orientação do vetor aceleração é a mesma do vetor força resultante. Então, o vetor aceleração está orientado na direção horizontal da esquerda para direta.

Força gravitacional: um caso especial da segunda Lei de Newton

As contribuições de Isaac Newton foram além do estabelecimento das bases da mecânica clássica, com os princípios que estamos estudando e que se estenderam para outras áreas do conhecimento, como a Matemática, a Óptica e a Astronomia.

Uma contribuição muito importante de Newton foi associar a queda de um objeto na superfície da Terra com a força que mantém os corpos celestes em suas órbitas. A lei encontrada por Newton para descrever essa força é denominada Lei da Gravitação Universal, dada pela seguinte expressão:

${\overrightarrow{F}}_g=-G\frac{m_1{m}_2}{R^2} \hat{r}$

Em que $m_1$ e $m_2$ são as massas dos corpos, $R$ é a distância entre os corpos, $G$ é constante de gravitação universal, com o valor $G=\mathrm{6,67}\times {10}^{-11} N{m}^2/k{g}^2$ e $\hat{r}$ é um versor sobre o eixo que liga os dois corpos, de modo que o sinal negativo da expressão indica a ação atrativa dessa força, em que $-\hat{r}$ aponta no sentido do corpo que atrai.

Então, a força responsável pela queda de um corpo nas proximidades da superfície da Terra será a força atrativa entre a massa da Terra e a massa do corpo.

Nas proximidades da superfície da Terra, o campo gravitacional é, aproximadamente, constante, com módulo $\left|\overrightarrow{g}\right|=\mathrm{9,8} m/s^2$. A força gravitacional que a Terra impõe aos corpos próximos à superfície é chamada de peso $\overrightarrow{P}=m\overrightarrow{g}$.

Siga em Frente...

Terceira lei de Newton: ação e reação

Esta lei de Newton nos auxilia no tratamento das forças que atuam entre dois corpos:

“Quando um corpo A exerce uma força sobre um corpo B (uma “ação”), o corpo B exerce uma força sobre o corpo A (uma ‘reação’). Essas duas forças têm o mesmo módulo e mesma direção, mas possuem sentidos opostos. Essas duas forças atuam em corpos diferentes” (Young; Freedman, 2016, p. 128).

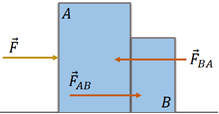
A Figura 2 ilustra o princípio da terceira lei, quando temos o contato dos corpos A e B. Ao empurrarmos um contra o outro, surgirá uma força ${\overrightarrow{F}}_{AB}$ que expressa a força que o bloco A aplica em B. Simultaneamente, o corpo B aplica uma força ${\overrightarrow{F}}_{BA}$ no corpo A como resposta. Então, essas forças configuram-se como um par ação-reação. Para esse par de forças, portanto, a terceira lei de Newton prevê que ambas as forças tenham o mesmo módulo, porém que sejam orientadas em sentidos contrários, ou seja, ${\overrightarrow{F}}_{AB}=-{\overrightarrow{F}}_{BA}$.

Exemplo: no sistema ilustrado na Figura 2, os corpos de massa $m_A=5 kg$ e $m_B=2 kg$ são empurrados por uma força de módulo $\left|\overrightarrow{F}\right|=20N$, aplicada no corpo de maior massa. Considere que as caixas podem se mover sem resistência do solo. De acordo com as leis de Newton, responda:

(a) Qual será o módulo da aceleração do sistema?

(b) Qual será a intensidade da força de contato entre os corpos?

Resolução:

(a) As forças que agem no bloco A é $\overrightarrow{F}$ e ${\overrightarrow{F}}_{BA}$, enquanto no bloco B age somente a força ${\overrightarrow{F}}_{AB}$. Observe que a força $\overrightarrow{F}$ atua apenas no primeiro bloco empurrando o bloco contra o bloco B. O corpo B se desloca pela ação do bloco A em B ${\overrightarrow{F}}_{AB}$, em contrapartida o bloco A recebe a reação ${\overrightarrow{F}}_{BA}$. Logo:

$\left\{\begin{array}{c}\left|\overrightarrow{F}\right|-{|\overrightarrow{F}}_{BA}|=m_A|\overrightarrow{a}| \\ {|\overrightarrow{F}}_{AB}|=m_B\left|\overrightarrow{a}\right| \end{array}\right.$

Mas ${|\overrightarrow{F}}_{AB}|={|\overrightarrow{F}}_{BA}|$, logo:

$\left|\overrightarrow{F}\right|-m_B\left|\overrightarrow{a}\right|=m_A\left|\overrightarrow{a}\right|$

$\left|\overrightarrow{F}\right|=m_A\left|\overrightarrow{a}\right|+m_B\left|\overrightarrow{a}\right|$

$\left|\overrightarrow{F}\right|={(m}_A+m_B) \left|\overrightarrow{a}\right|$

$\left|\overrightarrow{a}\right|=\frac{\left|\overrightarrow{F}\right|}{m_A+m_B}$

$\left|\overrightarrow{a}\right|=\frac{21}{5+2}$

$\left|\overrightarrow{a}\right|=3 m/s^2$

(b) ${|\overrightarrow{F}}_{AB}|=m_B\left|\overrightarrow{a}\right|$

${|\overrightarrow{F}}_{AB}|=2.3$

${|\overrightarrow{F}}_{AB}\left|={|\overrightarrow{F}}_{BA}\right|=6 N$

Vamos Exercitar?

Retomaremos a situação-problema apresentada no item Ponto de Partida: um disco de hóquei com massa de 0,30 kg desliza sobre a superfície horizontal sem atrito de uma pista de gelo. Dois bastões de hóquei batem no disco ao mesmo tempo, exercendo forças sobre ele, como mostrou a Figura 1. Como podemos determinar uma força resultante e queremos uma aceleração, esse problema é categorizado como um que pode ser resolvido usando a segunda lei de Newton.

Primeiro, precisamos encontrar a força resultante que age no disco de hóquei:

$\sum F_x=F_{1x}+F_{2x}=F_{1}cos\theta +F_2\cos \varphi = \mathrm{5,0}\cos \left(-20°\right)+\mathrm{8,0}\cos 60°=\mathrm{8,70} N$

$\sum F_y=F_{1y}+F_{2y}=F_{1}sen\theta +F_2\mathrm{sen}\varphi =\mathrm{5,0}sen\left(-20°\right)+\mathrm{8,0}\mathrm{sen}60°=\mathrm{5,22} N$

Podemos escrever a força resultante: ${\overrightarrow{F}}_R=\mathrm{8,70}\hat{i}+\mathrm{5,22}\hat{j}$

O módulo da força resultante é:

$F_R =\sqrt{F_x^2+F_y^2}=\sqrt{{\mathrm{8,70}}^2+{\mathrm{5,22}}^2} \to F_R =\mathrm{10,15} N$

Pela segunda lei de Newton:

$F_R=ma \to a=\frac{F_R}{m} \to a=\frac{\mathrm{10,15}}{\mathrm{0,30}} \to a=\mathrm{33,82} m/s^2$

Saiba Mais

Aprofunde seus conhecimentos!

A revolução provocada pelos trabalhos de Isaac Newton é descrita no texto do professor João Zanetic, da Universidade de São Paulo:

ZANETIC, J. Dos "Principia" da mecânica aos "Principia" de Newton. Caderno Catarinense de Ensino de Física, Florianópolis, n. 5, p. 23-25, jun. 1998.

Você já conhece as simulações interativas da Universidade de Colorado? As sims PhET baseiam-se em extensa pesquisa em educação e envolvem os alunos através de um ambiente intuitivo, estilo jogo, em que os alunos aprendem através da exploração e da descoberta. Acesse, em especial, os simuladores Forças e movimento: noções básicas, Laboratório de força gravitacional.

Referências Bibliográficas

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

KELLER, F. J.; GETTYS, W.; SKOVE, M. J. Física. São Paulo: Makron Books, 1997. v. 2.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

YOUNG, H. D.; FREEDMAN, R. A. Física I: mecânica. 14. ed. São Paulo: Person Education Brasil, 2016.

ZANETIC, J. Dos "Principia" da mecânica aos "Principia" de Newton. Caderno Catarinense de Ensino de Física, Florianópolis, n. 5, p. 23-25, jun. 1998. Disponível em: https://periodicos.ufsc.br/index.php/fisica/article/view/10072/9297. Acesso em: 25 jan. 2024.

Forças na natureza

Olá, estudante! Nesta videoaula, você trabalhará com a segunda lei de Newton. Essa lei é uma das três leis fundamentais formuladas por Sir Isaac Newton, que são a base da mecânica clássica. Ela descreve a relação entre a força resultante aplicada a um objeto, a massa desse objeto e a aceleração resultante. Isso significa que, se uma força externa agir sobre um objeto, ela causará uma aceleração proporcional à magnitude da força e inversamente proporcional à massa do objeto. Para encontrar a força resultante, torna-se necessário conhecer as forças que agem no objeto. Exemplos: força peso, força normal, força de tração, força elástica, força de atrito, entre outras.

Esse conteúdo é importante para a sua prática profissional, pois a segunda lei de Newton é fundamental para entender o movimento de objetos e é especialmente útil quando se trata de analisar sistemas sujeitos a forças externas. Ela permite prever o comportamento de um objeto sob a influência de forças conhecidas, ou calcular a força necessária para produzir uma certa aceleração.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Olá, estudante! Seja bem-vindo.

As forças são interações que podem causar uma mudança no movimento ou na forma de um objeto. Elas são fundamentais para a compreensão da física e são descritas pelas leis do movimento de Newton.

Existem várias formas de classificar as forças, dependendo do contexto em que estão sendo analisadas. As leis de Newton são frequentemente utilizadas para analisar e prever o comportamento dessas forças em diferentes situações.

Nesta seção, veremos apenas algumas categorias gerais, pois a variedade de forças na natureza é vasta. Cada tipo de força desempenha um papel específico em diferentes fenômenos físicos.

A fim de contribuir para compreensão dos conteúdos, propomos o seguinte problema: um semáforo pesando 122 N pende de um cabo ligado a dois outros presos a um suporte, como na Figura 1. Os cabos superiores formam ângulos de  ${\theta }_1$= 37,0° e  ${\theta }_2$= 53,0° com a horizontal. Esses cabos não são tão fortes quanto o cabo vertical e se quebrarão se a tensão neles for maior que 100 N. O semáforo permanecerá pendurado nesta situação, ou um dos cabos quebrará?

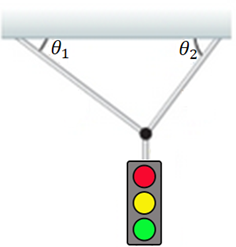
Para que você consiga resolver esse e outros problemas, é necessário que veja alguns conceitos sobre tipos de forças e, mais especificamente, sobre algumas regras que lhe permitirão calculá-las.

Então, vamos lá? Bons estudos!

Vamos Começar!

Na seção anterior, estudamos as leis de Newton, as quais nos permitem investigar diferentes tipos de sistemas mecânicos. Na presente seção, veremos que há casos especiais de forças que merecem destaque, pois são característicos de alguns sistemas, como a força elástica de molas ou a interferência da força de atrito entre objetos em contato.

Força peso

O planeta Terra exerce uma força de atração gravitacional em todos os corpos que possuem massa e que estejam no campo gravitacional dela. É essa força que faz os corpos caírem. Denominamos essa força de atração como peso ($\overrightarrow{P}$). A força peso sempre terá direção vertical e sentido para baixo, sendo perpendicular ao solo.

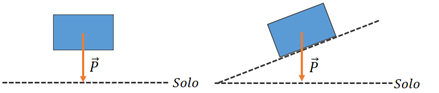
O peso de um corpo é dado por: $\overrightarrow{P}=m\overrightarrow{g}$, em que $m$ é a massa do objeto em kg e $\overrightarrow{g}$ é a aceleração da gravidade ($g\approx \mathrm{9,8} m/s^2$). O peso é uma força e, portanto, é medido na unidade newton (N). Observe que massa e peso são conceitos distintos, apesar de usarmos erroneamente no nosso dia a dia. O peso de um corpo não é a mesma coisa que a massa. A massa de um corpo é medida na unidade quilograma. O peso é uma força gravitacional, medido na unidade Newton. Portanto, se um objeto tem massa de $50 kg$, o módulo do peso, no planeta Terra, será: $P=50 . \mathrm{9,8}=490 N$.

Força normal

Quando um corpo exerce uma força sobre uma superfície qualquer, a superfície reage e empurra o corpo com uma força que é perpendicular à superfície. Essa força recebe o nome de força normal ($\overrightarrow{N}$). Assim sendo, sempre que um corpo estiver apoiado, a superfície de apoio exercerá uma força normal no corpo, sendo essa força sempre perpendicular à superfície de apoio.

A força normal recebe esse nome por causa de sua orientação vetorial sempre perpendicular à superfície de contato.

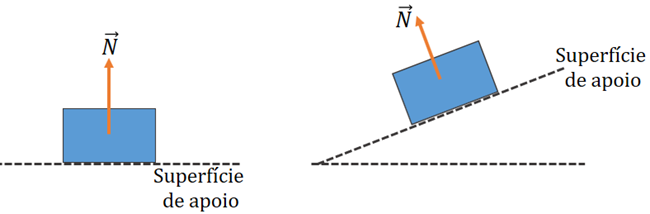
Para exemplificarmos a ação da força normal, podemos analisar a situação de uma pessoa que utiliza uma balança para medir sua massa. Ao subir, aplicará sobre ela uma força de mesma intensidade que a força peso. Em contrapartida, a balança devolverá essa ação com uma força de reação.

A força normal é resultado de uma característica intrínseca da matéria, a impenetrabilidade, uma vez que é impossível dois corpos ocuparem o mesmo espaço ao mesmo tempo. A pessoa, ao exercer força sobre a balança, será por ela empurrada para cima, e essa força de reação é a força que chamamos de normal. Assim, as forças normais aparecem na situação em que há o contato entre os corpos.

Força de tração

Outra forma comum de interação indireta entre os corpos é a conexão através de fios, cordas e cabos.

Quando o corpo está preso a uma corda (fio ou cabo) esticada, essa corda aplica ao corpo uma força denominada de tração ($\overrightarrow{T }$), que sempre estará orientada ao longo da corda, ou seja, terá a mesma direção dela. Trabalhamos aqui com cabos ideais, em que a massa do cabo e sua elasticidade são desprezíveis para o problema, de modo que todos os pontos apresentam uma tração orientada na direção do cabo tensionado, ou seja, a tração ao longo de um mesmo cabo ideal é constante.

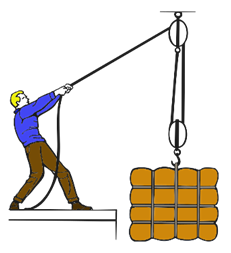
Observe, na imagem anterior, que uma pessoa puxa a corda. A corda resiste à deformação, puxando a extremidade oposta. Assim, como reação, a corda puxa o objeto ao qual está ligada.

Força elástica (mola)

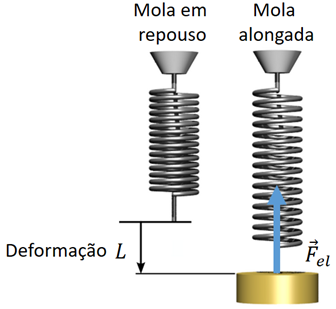
Quando um corpo está preso a um objeto elástico (mola, corda elástica ou outro objeto semelhante com propriedades elásticas), vale a Lei de Hooke, ou seja, o objeto elástico exerce uma força (${\overrightarrow{F}}_{el}$) sobre o corpo, proporcional à sua deformação ($\overrightarrow{L}$) e à sua constante elástica ($k$). Assim: ${\overrightarrow{F}}_{el}=-k\overrightarrow{L}$. A capacidade que um corpo apresenta de deformar-se quando submetido a uma força é expressa pela constante elástica.

A força elástica possui a mesma direção da deformação sofrida pelo objeto elástico, e o sentido dessa força é o da tendência de fazer o objeto elástico retornar à sua posição de repouso, ou seja, o sentido da força elástica é contrário ao sentido da deformação.

Siga em Frente...

Diagrama de corpo livre

Um diagrama de corpo livre (DCL) é uma representação gráfica usada na Física para analisar as forças que atuam sobre um objeto. Ele é particularmente útil para entender e resolver problemas de equilíbrio em corpos físicos. Aqui estão as etapas básicas para desenhar um diagrama de corpo livre:

• Identificação do corpo: comece identificando o corpo ou objeto de interesse. Isso pode ser uma partícula, um bloco, um corpo extenso etc.
• Isolamento do corpo: isole o corpo de todo o ambiente, destacando-o do restante do sistema. Isso simplifica a análise, concentrando-se apenas nas forças externas que agem sobre o corpo.
• Identificação das forças: identifique e desenhe todas as forças que atuam no corpo.
• Indicação das direções: indique a direção positiva para cada força. Isso ajuda a manter a consistência na análise. Por exemplo, se estiver trabalhando com um plano inclinado, você pode escolher uma direção para a força gravitacional ao longo do plano.
• Rotulação das forças: rotule cada força com uma letra para facilitar a referência na análise.
• Escolha do sistema de coordenadas: escolha um sistema de coordenadas apropriado para o problema. Isso pode envolver a escolha de eixos $x$ e $y$ para simplificar as expressões matemáticas.
• Análise de equilíbrio: se o corpo estiver em equilíbrio, as forças líquidas em cada direção devem ser zero. Use isso para resolver as equações e determinar desconhecidos.

Lembre-se de que a qualidade do DCL é crucial para uma análise precisa, então certifique-se de representar corretamente todas as forças envolvidas.

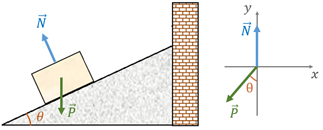
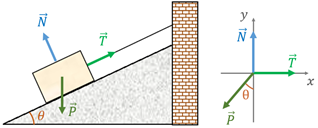
Exemplo: um bloco de massa 8,5 kg está pendurado em um plano inclinado (veja Figura 7). A inclinação do plano é 30°, e o plano não oferece atrito ao bloco. Determine a tensão na corda, a força normal sobre o bloco e a aceleração do bloco se a corda for cortada.

Resultado: o bloco está em repouso, logo:

$\sum F_x=0 \to \mathrm{ }T-P\mathrm{ }sen\left(30\right)=0 \to T-\mathrm{8,5}\mathrm{ }.\mathrm{ }\mathrm{9,8}\mathrm{ }.\mathrm{ }\mathrm{0,5}=0 \to T=\mathrm{41,7}\mathrm{ }N$

$\sum F_y=0 \to N-P\mathrm{ }cos\left(30\right)=0 \to N-\mathrm{8,5}\mathrm{ }.\mathrm{ }\mathrm{9,8}\mathrm{ }.\mathrm{ }\mathrm{0,866}=0 \to N=\mathrm{72,1}\mathrm{ }N$

Se a corda for cortada: $T=0$ ^® haverá movimento em $\left(-x\right)$.

$\sum F_x=m{a}_x \to -Psen\left(30\right)=\mathrm{8,5}{a}_x \to -\mathrm{8,5}\mathrm{ }.\mathrm{ }\mathrm{9,8}\mathrm{ }.\mathrm{ }\mathrm{0,5}=\mathrm{8,5}{a}_x \to a_x=-\mathrm{4,9}\mathrm{ }m/s^2$

Vamos Exercitar?

Retomaremos a situação descrita no início dessa seção.

Construímos um diagrama das forças que agem sobre o semáforo, mostrado na Figura 10a, e um diagrama de corpo livre para o nó que une os três cabos, mostrado na Figura 10c. O nó é um ponto conveniente para escolher, pois todas as forças de interesse agem ao longo de linhas que passam pelo nó.

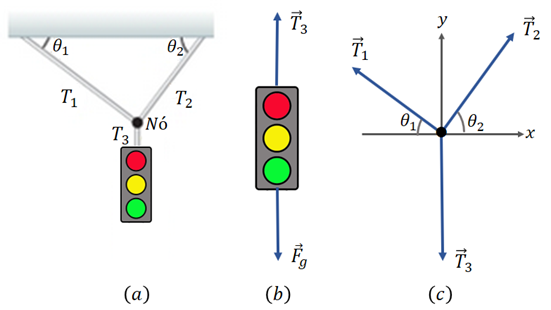
Podemos considerar, então, o semáforo uma partícula em equilíbrio, na qual a força resultante é zero. Decompondo as forças que agem sobre o nó em suas componentes:

${\overrightarrow{T}}_1=-T_{1}cos{\theta }_1\hat{i}+T_{1}sen{\theta }_1\hat{j} {\overrightarrow{T}}_2=-T_{2}cos{\theta }_2\hat{i}+T_{2}sen{\theta }_2\hat{j} {\overrightarrow{T}}_3=-F_g\hat{j}$

$\sum F_x=0 \to -T_{1}cos{\theta }_1=-T_{2}cos{\theta }_2 \to T_2=T_1\left(\frac{cos{\theta }_1}{cos{\theta }_2}\right)$

$\sum F_y=0 \to T_{1}sen{\theta }_1+T_{2}sen{\theta }_2-F_g=0 \to T_{1}sen{\theta }_1+T_1\left(\frac{cos{\theta }_1}{cos{\theta }_2}\right)sen{\theta }_2-F_g=0$

$T_1=\frac{F_g}{sen{\theta }_1+cos{\theta }_{1}tg{\theta }_2} \to T_1=\frac{122}{sen37°+cos37° tg53° } \to T_1=\mathrm{73,4} N$

$T_2=T_1\left(\frac{cos{\theta }_1}{cos{\theta }_2}\right) \to T_2=\mathrm{73,4}\left(\frac{cos37°}{cos53°}\right) \to T_2=\mathrm{97,4}$

Ambos os valores são menores que $100 N$, portanto os cabos não quebrarão.

Saiba Mais

Aprofunde seus conhecimentos!

Você já conhece as simulações interativas da Universidade de Colorado? As sims PhET baseiam-se em extensa pesquisa em educação e envolvem os alunos através de um ambiente intuitivo, estilo jogo, em que os alunos aprendem através da exploração e da descoberta. Acesse, em especial, os simuladores Forças e movimento: noções básicas, Massas e molas: básico e Lei de Hooke.

Para complementar seus estudos, acesse o Capítulo 5.1 do livro:

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

Referências Bibliográficas

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física, volume 1: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

HEWITT, P. G. Física conceitual. 13. ed. Porto Alegre: Bookman, 2023.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

TIPLER, P. A.; MOSCA, G. Física para cientistas e engenheiros: volume 1: mecânica, oscilações e ondas, termodinâmica. Rio de Janeiro: LTC, 2023.

Uso da primeira lei de Newton: partículas em equilíbrio

Olá, estudante! Nesta videoaula, você trabalhará com a primeira lei de Newton, conhecida também como Lei da Inércia. Ela é enunciada da seguinte maneira:

“Todo corpo permanece em seu estado de repouso ou movimento uniforme em linha reta, a menos que seja forçado a mudar esse estado por forças aplicadas sobre ele”.

Essa lei enfatiza o conceito de inércia, que é a propriedade de um objeto de resistir a mudanças em seu estado de movimento.

 Esse conteúdo é importante para a sua prática profissional, pois a primeira lei de Newton é fundamental para compreender o conceito de movimento e repouso, além de estabelecer a base para as leis subsequentes da mecânica.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Olá, estudante! Seja bem-vindo.

Você já conheceu a primeira lei de Newton: o princípio da inércia. Vimos que, se o corpo está em equilíbrio, a força resultante sobre ele deve ser nula. Agora que já aprendemos as três leis de Newton, estudaremos mais a fundo as situações de equilíbrio, aplicando a primeira lei de Newton. Realizaremos diversos exercícios para que você possa entender perfeitamente o que ocorre com objetos em tal estado.

Veremos que as aplicações da primeira lei de Newton possuem formas muito simples, porém capazes de solucionar uma grande variedade de desafios reais. No decorrer dos estudos, algumas dicas para solução de problemas serão apresentadas para que você se sinta mais confortável e acompanhe melhor o raciocínio.

Considere o seguinte problema: um carro de peso igual a 15.000 N está sendo puxado para cima, com velocidade constante, em uma rampa inclinada em 20°. O atrito é desprezível. A tensão máxima indicada pelo fabricante do cabo é de 6.000 N. O cabo se romperá?

Pronto para começarmos? Bons estudos!

Vamos Começar!

A primeira lei de Newton diz que há dois estados possíveis para um objeto sem força resultante sobre ele: diz-se que um objeto em repouso está em equilíbrio estático. Já um objeto que se move com velocidade constante está em equilíbrio dinâmico.

Na primeira lei de Newton do movimento, o que importa é conhecer a força resultante ${\overrightarrow{F}}_R,$ que é a somatória de todas as forças que atuam no objeto, sendo representada por:

$\sum _{i=1}^n{\overrightarrow{F}}_i={\overrightarrow{F}}_R \to {\overrightarrow{F}}_1+{\overrightarrow{F}}_2+{\overrightarrow{F}}_3+\dots ={\overrightarrow{F}}_R$

Quando a força resultante sobre um objeto é zero, dizemos que esse objeto está em equilíbrio, isto é, o objeto pode estar em repouso ou se movendo com velocidade constante.

$\sum _{i=1}^n{\overrightarrow{F}}_i={\overrightarrow{F}}_R=0 \to \mathrm{equilíbrio}.$

Antes de prosseguirmos, é importante enunciar que a equação ${\overrightarrow{F}}_R=0,$ como uma condição para o equilíbrio estático, realmente representa uma equação para cada dimensão do espaço de coordenadas que estamos considerando. Assim, no espaço tridimensional, temos três condições independentes de equilíbrio:

${\overrightarrow{F}}_{R,x}=\sum _{i=1}^n{\overrightarrow{F}}_{i,x}={\overrightarrow{F}}_{1,x}+{\overrightarrow{F}}_{2,x}+{\overrightarrow{F}}_{3,x}+\dots =0$

${\overrightarrow{F}}_{R,y}=\sum _{i=1}^n{\overrightarrow{F}}_{i,y}={\overrightarrow{F}}_{1,y}+{\overrightarrow{F}}_{2,y}+{\overrightarrow{F}}_{3,y}+\dots =0$

${\overrightarrow{F}}_{R,z}=\sum _{i=1}^n{\overrightarrow{F}}_{i,z}={\overrightarrow{F}}_{1,z}+{\overrightarrow{F}}_{2,z}+{\overrightarrow{F}}_{3,z}+\dots =0$

Lembre-se sempre do princípio da independência dos movimentos, ou seja, você pode e deve analisar separadamente o equilíbrio em cada eixo.

Porém, a primeira lei de Newton também inclui o caso de quando um objeto já está em movimento em relação a algum referencial específico. Para esse caso, a lei especifica que a aceleração é zero, contanto que a força externa resultante seja zero. Assim, podemos concluir: força resultante nula ⇔ velocidade constante (equilíbrio).

Para usar a primeira lei de Newton para uma situação de equilíbrio, você deve aplicá-la a um corpo específico. É necessário definir, logo de início, o corpo que será analisado.

Depois de identificar o corpo que será analisado, devemos identificar as forças que atuam sobre ele. Tenha em mente que:

• Se o corpo estiver em um campo gravitacional (planeta Terra), existe força peso ($\overrightarrow{P}$) atuando sobre ele.
• Se o corpo estiver apoiado em uma superfície, existe uma força normal ($\overrightarrow{N}$) atuando sobre ele.
• Se a superfície de contato não for perfeitamente lisa, existe uma força de atrito ($\overrightarrow{f }$) atuando sobre o corpo.
• Se o corpo estiver ligado por uma corda, fio ou cabo, existe uma tração ($\overrightarrow{T}$) atuando sobre ele.
• Se o corpo estiver ligado por uma corda elástica ou mola, existe uma força elástica (${\overrightarrow{F}}_{el}$) atuando sobre ele.

Você pode representar todas as forças que atuam no corpo a ser analisado por meio de um diagrama de corpo livre. Seja cuidadoso na hora de incluir todas as forças que atuam no objeto a ser analisado. Você só deve considerar as forças que são aplicadas nele. Tome cuidado para não considerar forças que o objeto aplica em outros corpos.

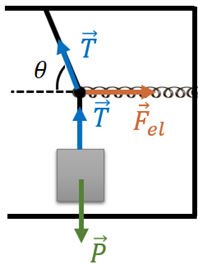
Exemplo: uma esfera está suspensa por uma corda e uma mola, como mostra a Figura 1. A mola está alongada em $20 cm$. Sabendo que a esfera está em equilíbrio e que a constante elástica da mola é $k=100 N/m$, calcule a tração e a massa da esfera.

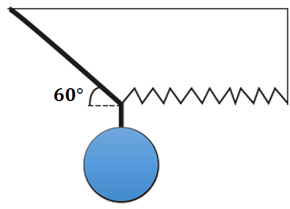
Siga em Frente...

Resolução: considerando que a situação ocorre no planeta Terra, temos força peso ($\overrightarrow{P}$) atuando sobre a esfera, sempre vertical para baixo. Como a esfera está suspensa por uma corda, temos a tração ($\overrightarrow{T}$) na direção do cabo. A esfera está suspensa, também, por uma mola, portanto temos a força elástica na mesma direção da mola e com sentido oposto ao da deformação. A Figura 2 mostra o diagrama de corpo livre da esfera.

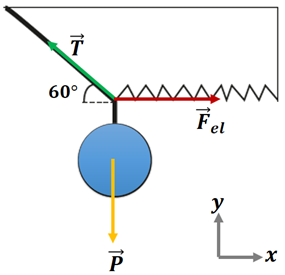
As forças envolvidas:

${\overrightarrow{F}}_{el}=kL \hat{i}$

$\overrightarrow{P}=-mg \hat{j}$

${\overrightarrow{T}}_x=-Tcos60° \hat{i}$

${\overrightarrow{T}}_y=Tsen60° \hat{j}$

Como a esfera está em equilíbrio, a somatória das forças que atuam sobre ela deve ser nula, ou seja, a força resultante deve ser zero.

No eixo $x$:

${\overrightarrow{F}}_{R,x}=kL \hat{i}- Tcos60° \hat{i}=0$

$kL=Tcos60°$

$T=\frac{kL}{cos60°}$

$T=\frac{100 .\mathrm{0,2}}{cos60°}$

$T=40N$

No eixo $y$:

${\overrightarrow{F}}_{R,y}=-mg \hat{j}+ Tsen60° \hat{j}=0$

$mg=Tsen60°$

$m=\frac{Tsen60°}{g}$

$m=\frac{40sen60°}{\mathrm{9,8}}$

$m=\mathrm{3,5} kg$

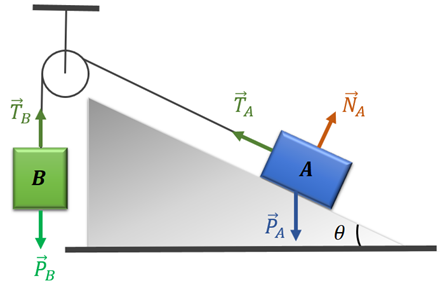
Exemplo: a Figura 3 mostra dois blocos, A e B. O bloco A está apoiado em um plano inclinado, enquanto o bloco B está preso ao A através de uma roldana. O sistema está em equilíbrio. O bloco A possui massa de $200 kg$. Considere o cabo, a roldana e o plano que apoia o bloco A como ideais (sem atrito, sem massa e inextensível). Encontre a massa do bloco B.

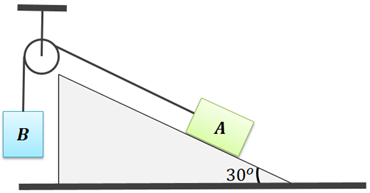
Resolução: primeiro, faremos o diagrama de corpo livre do sistema da Figura 3.

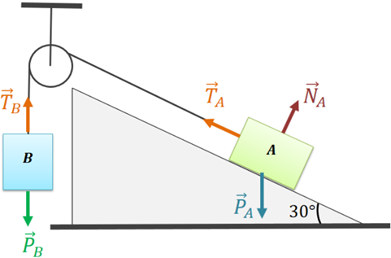
No bloco A  ⇒ $\sum {\overrightarrow{F}}_{R,A}=0$

$N_A=P_A\cos \left(30\right)$

$T_A=P_{A}sen\left(30\right)$

No bloco B  ⇒ $\sum {\overrightarrow{F}}_{R,B}=0$

$T_B=P_B$

Como : $T_A=T_B$

$P_{A}sen\left(30\right)=P_B$

$m_{A}gsen\left(30\right)=m_{B}g$

$m_B=m_{A}sen\left(30\right)$

$m=200sen\left(30\right)$

$m=100 kg$

Vamos Exercitar?

Retomaremos problema proposto: um carro de peso igual a 15.000 N está sendo puxado para cima, com velocidade constante, em uma rampa inclinada em 20°. O atrito é desprezível. A tensão máxima indicada pelo fabricante do cabo é de 6.000 N. O cabo se romperá?

Faremos o diagrama de corpo livre do problema. O sistema de coordenadas tem a mesma inclinação que a rampa. O eixo de movimento do carro (representado como um bloco na Figura 5) é o eixo $x$ do nosso diagrama. As forças que agem no carro: (a) o carro está em contato com a rampa, portanto há força normal $\overrightarrow{N}$; (b) o carro está no campo gravitacional da Terra, portanto há força peso $\overrightarrow{P}$; (c) o carro está sendo puxado por um cabo, portanto há força de tração $\overrightarrow{T}$.

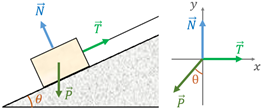
A velocidade do carro é constante, portanto, temos um equilíbrio dinâmico:

$F_{re{s}_x}=\sum F_x=T_x+N_x+P_x=0$

$F_{re{s}_y}=\sum F_y=T_y+N_y+P_y=0$

Do diagrama de corpo livre:

$T_x=T T_y=0 N_x=0 N_y=N P_x=-Psen\theta P_y=-Pcos\theta$

$F_{re{s}_x}=T-Psen\theta =0 \to T=Psen\theta \to T=\left(15000\right)sen20 \to T=5.130\mathrm{ }N$

Como o valor encontrado de $T$ é menor do que $6000 N$, o cabo não se romperá.

Saiba Mais

Aprofunde seus conhecimentos! Leia o Capítulo 5 do livro:

RESNICK, R.; HALLIDAY, D.; KRANE, K. S. Física 1. 5. ed. Rio de Janeiro: LTC, 2008. v. 1.

Referências Bibliográficas

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física, volume 1: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

RESNICK, R.; HALLIDAY, D.; KRANE, K. S. Física 1. 5. ed. Rio de Janeiro: LTC, 2008.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

YOUNG, H. D.; FREEDMAN, R. A. Física I: mecânica. 14. ed. São Paulo: Person Education Brasil, 2016.

Uso da segunda lei de Newton: dinâmica da partícula

Olá, estudante! Nesta videoaula, daremos continuidade ao estudo do equilíbrio, focando no equilíbrio dinâmico. Também, falaremos sobre a força de atrito e da força centrípeta. A força de atrito é uma força resistiva que age entre dois objetos em contato e se opõe ao movimento relativo ou à tendência de movimento relativo entre eles. A força centrípeta não é uma força separada, mas é frequentemente fornecida por outras forças, como a força gravitacional, a força de tensão em uma corda ou a força normal. Ela é fundamental para entender o movimento circular.

Esse conteúdo é importante para a sua prática profissional, pois o estudo do movimento é essencial em muitas áreas, incluindo física, engenharia, astronomia, biologia, entre outras.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Olá, estudante! Seja bem-vindo.

Em seções anteriores, vimos que existem várias categorias de forças na física, e elas são fundamentais para entender o comportamento dos objetos no universo. Aqui estão alguns tipos comuns de forças: força gravitacional, força normal, força de tração e força elástica. Esses são apenas alguns exemplos. Há muitos outros tipos de forças que podem ser específicos para determinados contextos ou teorias físicas mais avançadas.

Nesta seção, estudaremos as forças de atrito e a força centrípeta. O atrito ocorre quando dois objetos estão em contato e se opõem ao movimento relativo entre eles. A força centrípeta é a força que age em um objeto em movimento em uma trajetória circular.

No final desta seção, resolveremos o seguinte problema: na configuração mostrada na Figura 1, os blocos A e B possuem forças peso de, respectivamente, 980 N e 196 N. O sistema está em repouso. O coeficiente de atrito estático entre o bloco A e a superfície é de 0,30. Determine as forças de tração, a força normal e a força de atrito.

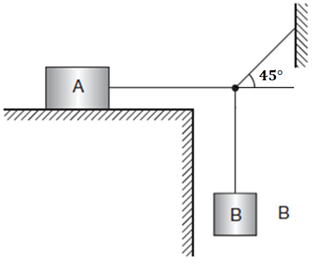
Lembre-se de que, ao analisar o movimento ou o repouso, é absolutamente necessário definir, logo de início, sobre qual corpo ou objeto estamos falando. Em seguida, devemos identificar todas as forças que atuam nesse corpo.

Revise os conceitos aprendidos nas seções anteriores. Vale muito a pena ter em mente tudo o que aprendemos até aqui. Acompanhe atentamente, a seguir, o que temos preparado para você. Divirta-se e bons estudos!

Vamos Começar!

Em seções anteriores, vimos que existem várias categorias de forças na física, e elas são fundamentais para entender o comportamento dos objetos no universo. Aqui estão alguns tipos comuns de forças: força gravitacional, força normal, força de tração e força elástica.

Agora, veremos mais dois tipos: força de atrito e força centrípeta. O atrito ocorre quando dois objetos estão em contato e se opõem ao movimento relativo entre eles. Existem dois tipos principais de atrito: atrito estático (quando os objetos estão em repouso relativo) e atrito cinético (quando os objetos estão em movimento relativo). A força centrípeta é a força que age em um objeto em movimento em uma trajetória circular. Essa força é direcionada para o centro da trajetória circular.

Força de atrito

A força de atrito é causada pelas irregularidades microscópicas nas superfícies dos objetos. Essas asperezas impedem ou dificultam o deslizamento suave entre os corpos. A força de atrito atua sempre no sentido oposto à direção do movimento relativo entre as superfícies, resistindo à tentativa de escorregamento. Esse fenômeno é uma parte fundamental da física e tem implicações significativas em muitos aspectos da vida cotidiana, desde o movimento de veículos até a simples ação de caminhar. A compreensão da força de atrito é essencial para projetar máquinas, prever o comportamento de objetos em movimento e otimizar diversos processos.

A ação do atrito pode ocorrer de duas maneiras: por meio do atrito estático (${\overrightarrow{f}}_e$) e do atrito cinético (${\overrightarrow{f}}_c$). O atrito estático ocorre quando não há o deslizamento entre as superfícies, evitando que haja o movimento. A força de atrito estático cancela totalmente a força aplicada sobre o corpo, até um determinado limite. O módulo da força de atrito estático é calculado pela expressão:

$\left|{\overrightarrow{f}}_e\right|\le {\mu }_e\left|\overrightarrow{N}\right|$

Em que ${\mu }_e$ é o coeficiente de atrito estático, que depende das características de cada superfície de contato, tais como rugosidade, temperatura e composição. Esses valores não apresentam unidade, ou seja, são adimensionais. Além disso, os coeficientes de atrito sempre assumem valores entre 0 e 1. Essa expressão é uma desigualdade, pois a intensidade do atrito estático é variável até um valor limite:

$\left|f_{e,max}\right|={\mu }_e\left|\overrightarrow{N}\right|$

Isso significa que, se a força de atrito estático máximo para um par de superfícies for 50N, não haverá movimento até que a força externa seja superior a esse valor. Se aplicarmos uma força externa de 30 N, a força de atrito estático será de 30 N (abaixo do valor máximo), em um cancelamento que mantém o estado de repouso.

Na fase de movimento, a força de atrito passa a ser denominada como força de atrito cinético (${\overrightarrow{f}}_c$), cuja expressão matemática para seu módulo é:

$\left|{\overrightarrow{f}}_c\right|={\mu }_c\left|\overrightarrow{N}\right|$

Observe que ${\mu }_c$ é o coeficiente de atrito cinético. Essa força tem intensidade constante durante o movimento. Podemos representar a evolução da força de atrito agindo em um corpo em um gráfico, quando submetido a uma força externa de intensidade crescente. Há uma descontinuidade no gráfico, pois o valor máximo do coeficiente de atrito estático é superior ao de atrito cinético.

Figura 2 | Representação da evolução da força de atrito quando um corpo é submetido a uma força externa $F$ de intensidade crescente

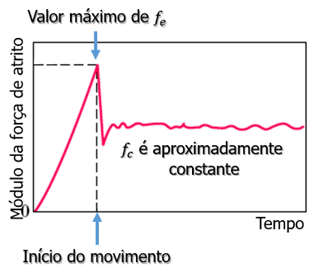
Força centrípeta

De acordo com a segunda lei de Newton, o movimento de um corpo é gerado pela ação de uma força resultante que produzirá aceleração, com ambos os vetores na mesma direção. No caso do movimento circular, essa força é a força centrípeta, dada por:

$\left|{\overrightarrow{F}}_{cp}\right|=m\left|{\overrightarrow{a}}_{cp}\right| \to \left|{\overrightarrow{F}}_{cp}\right|=\frac{m{\left|\overrightarrow{v}\right|}^2}{R}$

Um ponto importante é que a força centrípeta é sempre o resultado da ação de outras forças, como a tração ou a força peso, entre outras, que agem em determinado momento, mantendo a trajetória circular do corpo.

Podem ser consideradas como trajetórias circulares o movimento de carros em lombadas, depressões na pista, entre outros. Um exemplo é o globo da morte, em que uma pessoa com uma moto anda pelas paredes de um globo de metal e por várias vezes passa pelo ponto mais alto. Em condições normais, ao passar por esse ponto, o corpo estaria suspenso e deveria cair pela ação do campo gravitacional, porém a resultante centrípeta nos ajuda a entender como é possível completar o loop sem a queda.

A Figura 3 ilustra um esquema representativo do globo da morte em dois pontos importantes: o primeiro no ponto mais baixo da trajetória e o segundo na posição oposta, com os vetores peso e normal em cada momento.

Figura 3 | Representação dos vetores $\overrightarrow{N}$ e $\overrightarrow{P}$ em diferentes pontos do corpo no globo da morte

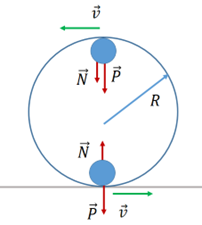
Então, na posição mais baixa, a força normal e o peso compõem a força resultante centrípeta. Como esta deve ser direcionada para o centro da trajetória, teremos a seguinte equação: $\left|\overrightarrow{N}\right|-\left|\overrightarrow{P}\right|=m\left|{\overrightarrow{a}}_{cp}\right|$. No ponto mais alto da trajetória, a força resultante centrípeta tem como equação: $\left|\overrightarrow{N}\right|+\left|\overrightarrow{P}\right|=m\left|{\overrightarrow{a}}_{cp}\right|$. Dessa forma, este corpo está em condições de despencar a qualquer momento, porém o vetor velocidade tem papel importante para manter a trajetória do corpo. Para completar o loop, o motociclista precisa manter uma velocidade alta, para que o movimento composto da queda com a velocidade da moto faça com que ele siga a trajetória circular.

Então, haverá uma velocidade mínima para que seja possível completar o loop. Nesta condição, dizemos que o corpo está na eminência de perder o contato com a superfície, ou seja, a força normal entre o globo e a moto é quase nula. Inserida esta suposição, na segunda lei de Newton, podemos encontrar a seguinte relação:

$\left|\overrightarrow{N}\right|+\left|\overrightarrow{P}\right|=m\left|{\overrightarrow{a}}_{cp}\right| \to 0+m\left|\overrightarrow{g}\right|=\frac{m{\left|\overrightarrow{v}\right|}^2}{R} \to \left|\overrightarrow{v}\right|=\sqrt{\left|\overrightarrow{g}\right|R}$

Perceba que a velocidade mínima para completar a volta depende do raio da trajetória e é independente da massa do corpo.

Siga em Frente...

Uso da segunda lei de Newton: dinâmica da partícula

Você já aprendeu como resolver situações em que os objetos estavam em equilíbrio. Agora, aprenderemos como resolver situações em que o corpo não está em equilíbrio, ou seja, discutiremos problemas de dinâmica. Os corpos que não estão em equilíbrio se aceleram, pois, sobre eles, atua uma força resultante diferente de zero, conforme enunciado pela segunda lei de Newton.

A segunda lei de Newton define o princípio fundamental da dinâmica: a força resultante que age sobre um corpo é igual ao produto da massa do corpo pela aceleração. Assim, devemos lembrar que:

$\sum \overrightarrow{F}={\overrightarrow{F}}_r=m\overrightarrow{a}$

Para resolver as situações da dinâmica de corpos, primeiro é preciso identificar o corpo que estudaremos; em seguida, devemos descobrir todas as forças que atuam sobre ele. Ajuda muito desenhar um diagrama de corpo livre com os sentidos positivos dos eixos do plano cartesiano. Uma dica importante é lembrar que a força resultante e a aceleração sempre possuem mesma direção e sentido.

Exemplo: um condutor envolvido em um acidente relatou à polícia que estava trafegando em uma curva plana com velocidade de $70 km/h$. Apesar da baixa velocidade e do tempo bom, ele acabou derrapando na pista e parou no canteiro. Mas, será que o relato do motorista, de fato, está correto?

O policial que estava investigando o acidente coletou os seguintes dados: a curva tem raio igual a $80 km$, o coeficiente de atrito estático entre o pneu e o asfalto é de $\mathrm{0,5}$ e a marca de derrapagem se estende por, aproximadamente, $50 m$.

O diagrama de corpo livre é mostrado na Figura 5.

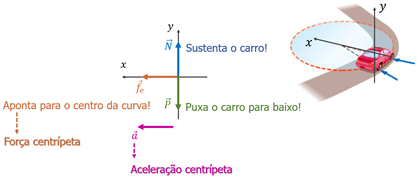
Temos que: ${\overrightarrow{F}}_R=m\overrightarrow{a}$

Não há movimento em $y$:

${\overrightarrow{F}}_y=0 \to N=P=mg$

Em $x$:

${\overrightarrow{F}}_{Rx}=m\overrightarrow{a} \to f_e=ma$

A força de atrito se comporta como uma força centrípeta, pois está direcionada para o centro da trajetória:

$f_e={\mu }_{e}N$

$F_{cp}=\frac{m{v}^2}{R}$

${\mu }_{e}mg=\frac{m{v}^2}{R}$

$v=\sqrt{R{\mu }_{e}g} \to v=\sqrt{\left(80\right)\left(\mathrm{0,5}\right)\left(\mathrm{9,8}\right)} \to v=\mathrm{19,8} m/s \to v\cong 71 km/h$ 

Essa velocidade é a máxima possível para o carro completar a curva, caso contrário a força de atrito não será suficiente para ajudar o carro a terminar a curva, causando a derrapagem. Então, a velocidade relatada pelo condutor é inferior ao máximo da pista, o que não deveria provocar a derrapagem do carro

O próximo passo é obter a velocidade real do carro, considerando que ele começou a derrapar com as rodas travadas. Assim, a força de atrito passa a atuar contra o movimento, freando o carro na distância de $50 m$.

$f_e=m{a}_{cp} \to a_{cp}={\mu }_{e}g \to a_{cp}=\left(\mathrm{0,5}\right)\left(\mathrm{9,8}\right) \to a_{cp}=\mathrm{4,9} m/s^2$

$v^2=v_0^2-2a_{cp}∆x v=0$

$v_0=\sqrt{2a_{cp}∆x} \to v_0=\sqrt{2\left(\mathrm{4,9}\right)\left(50\right)} \to v_0=\mathrm{22,1} m/s \to v_0\cong 80 km/h$

A velocidade inicial do carro é superior à que a curva permite, o que ocasionou a derrapagem do carro.

Vamos Exercitar?

Retomaremos o exercício proposto no início dessa seção: na configuração mostrada na Figura 6, os blocos A e B possuem forças peso de, respectivamente, 980 N e 196 N. O sistema está em repouso. O coeficiente de atrito estático entre o bloco A e a superfície é de 0,20. Determine as forças de tração, a força normal e a força de atrito.

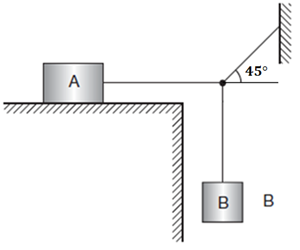
O diagrama de corpo livre do exercício é mostrado na Figura 7.

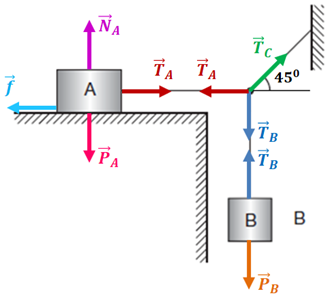
O sistema está em equilíbrio, logo, baseado no diagrama de corpo livre:

$\sum {\overrightarrow{F}}_B=0 \to {\overrightarrow{T}}_B-{\overrightarrow{P}}_B=0 \to T_B=P_B=196N$

$\sum {\overrightarrow{F}}_{nó}=0 \to \left\{\begin{array}{c}{T}_{C,y}-T_B=0\\ T_{c,x}-T_A=0\end{array}\right. \to \left\{\begin{array}{c}{T}_c sen\left({45}^0\right)=T_B\\ T_c cos\left({45}^0\right)=T_A\end{array}\right.\mathrm{ } \to T_A=T_B=196N$

$\sum {\overrightarrow{F}}_A=0 \to \mathrm{ }\left\{\begin{array}{c}{N}_A-P_A=0 \\ f-T_A=0 \end{array}\right. \mathrm{ }\to \left\{\begin{array}{c}{N}_A=P_A=980N \\ f=T_A=196N \end{array}\right.$

Poderíamos determinar o coeficiente de atrito pela equação $f={\mu }_e{N}_A$, ou seja, $f=\mathrm{0,2} . 980=196 N.$ Logo, a força de atrito tem módulo igual a 196 N, direção horizontal e sentido da direita para a esquerda.

Saiba Mais

Aprofunde seus conhecimentos!

Como sugestão, recomendamos a leitura das páginas 157 até 160 do livro indicado a seguir, no qual há uma discussão mais aprofundada sobre a força de atrito:

YOUNG, H. D.; FREEDMAN, R. A. Física I: mecânica. 14. ed. São Paulo: Person Education Brasil, 2016.

Você pode também acessar as páginas 129 e 131 do seguinte livro:

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física, volume 1: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

Há diversas aplicações de sistemas com trajetórias circulares, nas quais a resultante centrípeta é a composição das forças que atuam nos corpos. Nas páginas 138 até 143 do livro a seguir, há uma discussão aprofundada sobre o tema e com alguns exemplos resolvidos:

TIPLER, P. A.; MOSCA, G. Física para cientistas e engenheiros. 6. ed. São Paulo: LTC, 2009.

Referências Bibliográficas

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física, volume 1: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

HEWITT, P. G. Física conceitual. 13. ed. Porto Alegre: Bookman, 2023.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

TIPLER, P. A.; MOSCA, G. Física para cientistas e engenheiros: volume 1: mecânica, oscilações e ondas, termodinâmica. Rio de Janeiro: LTC, 2023.

Videoaula de Encerramento

Olá, estudante! Nesta videoaula, você conhecerá as três leis de Newton. As leis de Newton, formuladas por Sir Isaac Newton no século XVII, são três princípios fundamentais que constituem a base da mecânica clássica. Elas descrevem o movimento dos corpos e a relação entre a força aplicada sobre um objeto e sua resposta em termos de movimento. Estudaremos casos de equilíbrio, tanto equilíbrio estático como dinâmico.

Esse conteúdo é importante para a sua prática profissional, pois, juntas, as leis de Newton fornecem uma descrição abrangente do movimento e da dinâmica dos objetos. Essas leis são fundamentais para a física clássica e continuam sendo amplamente aplicadas em uma variedade de campos, proporcionando uma base sólida para a compreensão do comportamento de corpos em movimento e a interação entre forças.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Chegada

Olá, estudante!

Para desenvolver a competência desta unidade, ou seja, compreender as grandezas fundamentais da dinâmica e saber aplicar os conceitos gerais envolvendo as leis de Newton, você deverá, primeiramente, conhecer as três leis do movimento de Newton: a lei da inércia, o princípio fundamental da dinâmica e a lei de ação e reação.

As leis de Newton são três princípios fundamentais formulados por Sir Isaac Newton no século XVII que descrevem o movimento dos corpos e as forças que atuam sobre eles. Elas são a base da mecânica clássica e são amplamente utilizadas na física para explicar o comportamento de objetos em movimento.

Para algumas aplicações das leis de Newton, é necessário conhecer alguns tipos de força presentes na natureza. As mais comuns são: força gravitacional, força normal, força de tração, força elástica, força de atrito e força centrípeta. Essas são apenas algumas das forças mais comuns. Em diferentes situações, outras forças específicas podem estar envolvidas, dependendo do contexto físico em questão.

É Hora de Praticar!

Agora já sabemos como descobrir as forças que atuam em um corpo e aprendemos sobre a terceira lei de Newton, estudaremos e aplicaremos os conceitos aprendidos na situação de uma empresa na qual você e sua equipe realizarão estudos e simulações durante a instalação de um elevador em um prédio.

Seu primeiro desafio será analisar e calcular as forças que atuam no elevador quando ele está no processo de subida, a partir do repouso, até atingir a velocidade constante.

Um segundo desafio será analisar o que acontece com o elevador em duas situações de equilíbrio: em repouso e em movimento uniforme. Vocês definirão, também, o número máximo de passageiros que o elevador pode suportar, sabendo que a tração máxima no cabo é de $20 kN$.

O elevador é sustentado e acionado por um cabo que liga o elevador ao motor e ao contrapeso. A massa do elevador é de $800 kg,$ e a do passageiro, que participa das simulações, é de $70 kg$. A aceleração do elevador na subida, partindo do repouso até atingir a velocidade constante, é igual a $\mathrm{2,0} m/s^2$.

Reflita

Testes rápidos

1. Você conseguiria explicar por que sua mão ou seu pé machucam quando você bate em uma parede? Por qual motivo os lutadores usam luvas nas mãos?
2. Você está brincando com sua filha na neve. Ela se senta em um trenó e pede que você a faça deslizar por um campo horizontal, plano. Você pode optar por (a) empurrá-la por trás, aplicando uma força para baixo sobre os ombros dela a 30° abaixo da horizontal, ou (b) prender uma corda na frente do trenó e puxar com uma força a 30° acima da horizontal. O que seria mais fácil para você e por quê?
3. Suponha que você esteja falando, através de um telefone interplanetário, com um amigo que mora na Lua. Ele diz que acabou de ganhar um newton de ouro em uma competição. Excitadamente, você lhe diz que entrou na versão terrena da mesma competição. Quem é mais rico? (a) Você. (b) Seu amigo. (c) Os dois são igualmente ricos.

Resolução do estudo de caso

Temos a seguinte situação: uma pessoa de $80 kg$ está em um elevador que sobe e desce com a aceleração de $2 m/s^2$ e sobe com a aceleração $4 m/s^2$.

A Figura 1 apresenta essa situação com as representações dos vetores peso e normal.

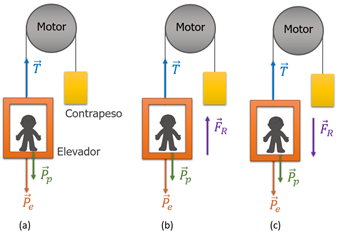
Os movimentos estão apenas na direção vertical, então podemos escrever a segunda lei de Newton para cada caso como:

$F_{R,subida}=ma \to N-\left(P_e+P_p\right)=ma$

$F_{R,descida}=ma \to N-\left(P_e+P_p\right)=-ma$

Substituindo os valores numéricos, teremos que o módulo da força normal em cada caso será de:

$F_{R,subida} \to N=\left(P_e+P_p\right)+ma \to N=\left(800+70\right) . \mathrm{9,8}+\left(800+70\right) . 2=10266 N$

$F_{R,descida} \to N=\left(P_e+P_p\right)-ma \to N=\left(800+70\right) . \mathrm{9,8}-\left(800+70\right) . 4=5046 N$

A tração no cabo, no momento da descida, partindo do repouso até atingir a velocidade constante, possui módulo de $10266 N,$ e no momento da descida é de $5046 N$.

Agora, analisaremos a situação em que o elevador está em equilíbrio (repouso ou se movendo com velocidade constante). Logo:

$T=P_p+P_e \to T=\left(800+70\right).\mathrm{9,8} \to 8526 N$

Portanto, o módulo da tração para o elevador em equilíbrio é $8526 N$.

Vemos, então, que a maior tração no cabo ocorre no processo de subida do elevador, ou seja, quando ele parte do repouso e acelera para subir, até atingir a velocidade constante.

O peso máximo suportado é:

$T_{max}-P_{max}=m_{limite}.a \to 20000-\left(m_{limite} . \mathrm{9,8}\right)=m_{limite} .2 \to m_{limite}=\frac{20000}{\mathrm{11,8}}$

$m_{limite}\approx 1695 kg$

Dessa massa total, $800 kg$ é da cabine do elevador. Assim, o número máximo de passageiros, considerando a média de massa de $70 kg$ por passageiro, é:

$\mathrm{Passageiros}=\frac{1695-800}{70}\approx \mathrm{12,8} \to 12 \mathrm{passageiros}$

Dê o play!

Assimile

A imagem a seguir apresenta um mapa mental que sintetiza os principais conceitos abordados na unidade. Um mapa mental é uma representação gráfica e visual de ideias e conceitos, geralmente centrado em torno de uma palavra-chave ou ideia central. Ele é uma ferramenta eficaz para organizar informações, estimular a criatividade e facilitar o aprendizado.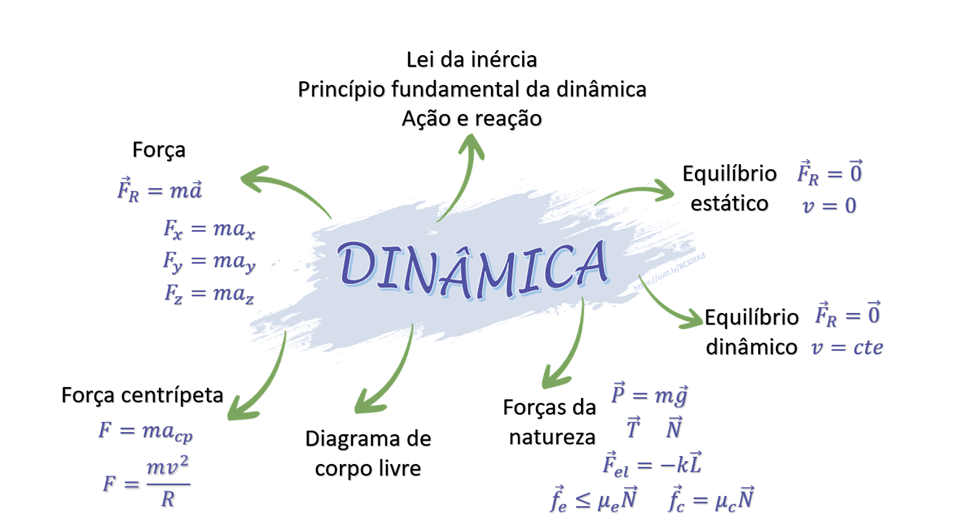

Referências

BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física, volume 1: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

HEWITT, P. G. Física conceitual. 13. ed. Porto Alegre: Bookman, 2023.

SERWAY, R. A.; JEWETT JR., J. W. Física para cientistas e engenheiros: volume 1: mecânica. São Paulo: Cengage Learning, 2017.

TIPLER, P. A.; MOSCA, G. Física para cientistas e engenheiros: volume 1: mecânica, oscilações e ondas, termodinâmica. Rio de Janeiro: LTC, 2023.