Estruturas cristalinas

Estrutura cristalina e sistemas cristalinos

Olá, Estudante! Nessa videoaula serão abordados os conceitos de estrutura cristalina e sistemas cristalinos, bem como as definições que permeiam esse tema. Você irá compreender que, na formação de materiais, podemos ter estruturas cujos átomos/moléculas apresentam um ordenamento atômico de curto, médio ou longo alcance. E esse ordenamento, conhecido como arranjo atômico apresenta papel importante na determinação da microestrutura de um material.

Esses conceitos e definições são importantes para sua prática profissional, pois compreender com a microestrutura do material é formada auxilia na determinação e análise das propriedades de um material. Assim, identificando as propriedades é possível a correta seleção de um material para sua devida aplicação.

Vamos juntos entender melhor esses conceitos?!Bons estudos!!!

Ponto de Partida

Olá, Estudante! Nessa aula entenderemos como ocorre a organização de átomos na formação de um material e como isso influencia em suas propriedades. Veremos que há materiais amorfos e cristalinos e, para sistemas cristalinos, há 7 sistemas, totalizando 14 tipos de redes possíveis de ordenamento atômico, cada uma com características específicas. E ainda, vamos focar nosso estudo na estrutura cristalina dos metais, avaliando a disposição dos átomos, características e propriedades desse ordenamento.

Dessa forma, compreenderemos que as propriedades de alguns materiais estão diretamente relacionadas com estrutura cristalina que possui. Por exemplo, o magnésio puro é mais frágil que a prata, devido ao tipo de estrutura cristalina que possui.

Além disso, existem diferenças significativas de propriedades entre materiais cristalinos e não cristalinos que possuem a mesma composição. Por exemplo, as cerâmicas e os polímeros não cristalinos são, em geral, opticamente transparentes, mas os mesmos materiais na forma cristalina (ou semicristalina) tendem a ser opacos ou translúcidos.

Assim, visando a aplicação desses conceitos, considere uma situação em que você faz parte de uma grande empresa que visa desenvolver projetos inovadores, utilizando as tecnologias oferecidas no mercado, buscando sempre os melhores materiais para utilização, visando qualidade e custo-benefício.

Nesse momento, a equipe em que você faz parte está desenvolvendo um equipamento óptico e cogitou a possibilidade da utilização de ródio para evidenciar algumas propriedades específicas. Como nota de curiosidade, o ródio, nos últimos tempos, tem se tornando um metal precioso de grande custo e valia, já que pode ser utilizado na indústria eletrônica em alguns equipamentos ópticos e em certos tipos de espelhos, e ainda, na joalheria é utilizado em quantidades muito pequenas para aumentar a resistência do ouro e lhe dar uma aparência mais brilhante.

Dessa forma, solicitaram que você realizasse uma pesquisa quanto o ordenamento atômico desse material, informando qual a estrutura cristalina que possui, o valor do parâmetro de rede, volume e FEA. Feito isso, calcular a massa específica para esse material.

Vamos conhecer os conceitos necessários para resolução do problema proposto? Bons estudos!

Vamos Começar!

Conceitos fundamentais

Na formação dos materiais, independentemente do estado físico da matéria, os átomos e/ou íons podem se organizar em três tipos de arranjos diferentes: sem ordem, ordem de curto alcance e ordem de longo alcance. Como exemplo, os gases inertes monoatômicos não possuem ordenação regular dos átomos. Entretanto, algumas substâncias, como vapor d’água e vidro de silicato, possuem ordem de curto alcance. Já metais, ligas metálicas, várias cerâmicas e alguns polímeros exibem ordenação regular de átomos/íons, que se estende por todo o material (ordenamento de longo alcance). Vejamos cada ordenamento separadamente:

• Sem ordem: materiais que não possuem ordenamento atômico são considerados sem ordem, pois eles preenchem aleatoriamente todo o espaço no qual o material está confinado. Exemplo: materiais em estado gasoso.
• Ordem de curto alcance: materiais que possuem ordenamento de curto alcance são aqueles em que o arranjo espacial dos átomos se estende apenas aos vizinhos mais próximos de cada átomo. Materiais que apresentam esse tipo de ordenamento são conhecidos como amorfos.
• Ordem de longo alcance: materiais em que o arranjo atômico espacial se estende por todo material e os átomos formam um padrão regular, repetitivo, como grades ou redes. Materiais que exibem esse comportamento são denominados de cristalinos.

Dessa forma, podemos dizer que os materiais, no estado sólido, podem ser classificados de acordo com a regularidade pela qual seus átomos ou íons estão arranjados uns em relação aos outros (curto ou longo alcance).

Os materiais amorfos, que apresentam ordenamento de curto alcance, se formam quando o processo de fabricação não permite a organização dos átomos em arranjos periódicos. No geral, eles apresentam uma combinação exclusiva de propriedades para cada material, pois os átomos ou íons não estão dispostos em seus arranjos regulares e periódicos.

Os materiais cristalinos são aqueles em que os átomos estão posicionados segundo um arranjo periódico repetitivo ao longo de grandes distâncias atômicas, podendo contemplar todo material. Todos os metais, muitos materiais cerâmicos e certos polímeros formam estruturas cristalinas sob condições normais de solidificação.

Se o material cristalino for composto por um único cristal, recebe o nome de monocristalino, ou monocristal.  Contudo, existem materiais cristalinos composto de várias pequenas regiões com diferentes orientações espaciais, denominados de materiais policristalinos, ou simplesmente policristal. Esses cristais menores que compõe o material são conhecidos como grãos e as fronteiras entre essas regiões em que há a mudança de direção nos cristais recebem o nome de contornos de grão.

A maneira com a qual os átomos, íons ou moléculas estão arranjados no espaço na formação do material impacta diretamente em algumas das propriedades dos sólidos cristalinos. Ou seja, algumas características dos materiais dependem do tipo de estrutura cristalina que apresentam.

São muitas as formas possíveis para a estrutura cristalina nos materiais, estando presente em todas elas o ordenamento atômico de longo alcance. Essas estruturas variam com formas mais simples (apresentadas pelos metais) até as excessivamente complexas, como aquelas exibidas por alguns materiais cerâmicos e poliméricos. Contudo, vamos focar nossos estudos nas estruturas cristalinas comumente apresentadas pelos materiais metálicos.

Para compreender e descrever as estruturas cristalinas, em nossos estudos, vamos considerar os átomos (ou íons) como esferas sólidas de diâmetros bem definidos. Esse método é conhecido como modelo atômico da esfera rígida e considera que as esferas que representam os átomos vizinhos mais próximos se tocam umas nas outras.

Células unitárias e estrutura cristalina nos metais

O ordenamento de longo alcance em materiais sólidos cristalinos indica que pequenos grupos de átomos formam um padrão que se repete ao longo do material. Assim, quando descrevemos uma estrutura cristalina, é interessante subdividir a estrutura total em pequenas entidades que se repetem, chamadas células unitárias, ou seja, a menor unidade de repetição na formação de um cristal. Um exemplo para ilustrar esse conceito pode ser dado pela análise de uma pilha de tijolos. Se essa pilha de tijolos fosse um cristal, um único tijolo seria definido como a célula unitária, que se repete tridimensionalmente para a formação do material completo.

De modo geral, as células unitárias possuem seis lados, sendo cada lado um paralelogramo. Por convenção, admite-se que os átomos ou íons são esferas sólidas e com diâmetros definidos, e que os vértices do paralelogramo devem coincidir com os centros de massa dos átomos.

Uma célula unitária é escolhida para representar a simetria da estrutura cristalina, de forma que todas as posições dos átomos no cristal possam ser geradas por translações da célula unitária segundo fatores inteiros de distância ao longo de cada uma das suas arestas. Nesse sentido, a célula unitária é a unidade estrutural básica, ou bloco construtivo, da estrutura cristalina e define a estrutura cristalina por meio da sua geometria e das posições dos átomos no seu interior.

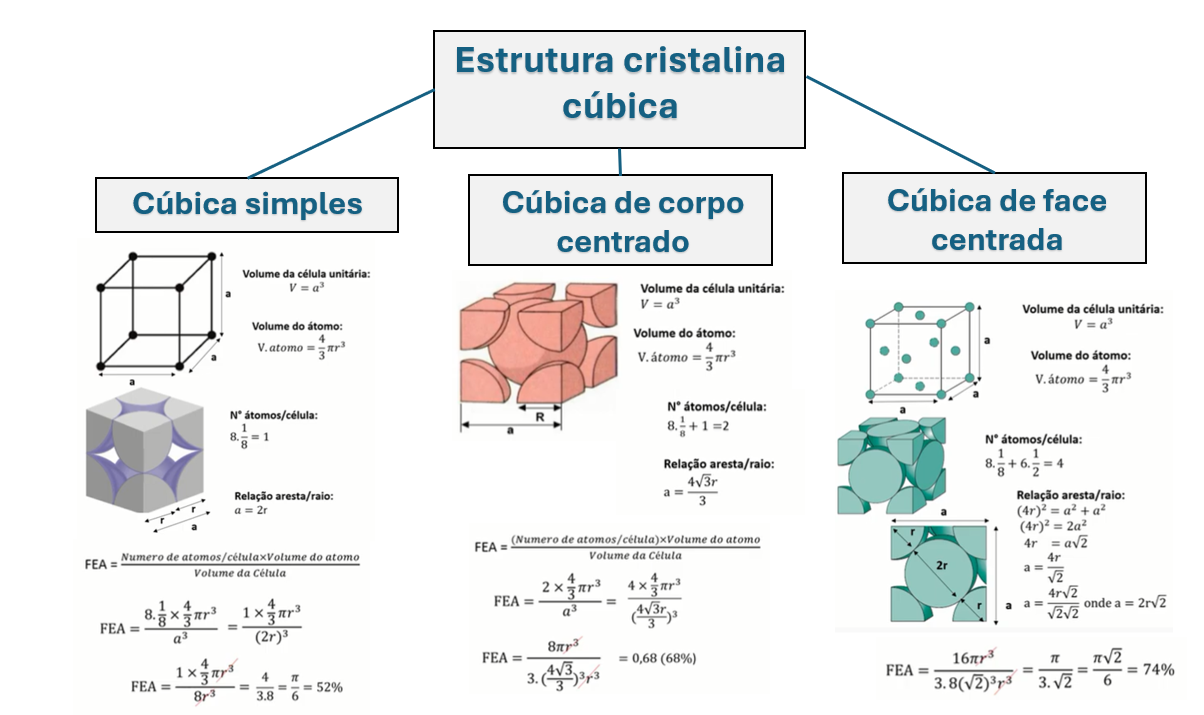
Vamos analisar as estruturas cristalinas comuns para os materiais metálicos. Materiais desse tipo podem se solidificar em estruturas cristalinas que apresentam quatro tipos de células unitárias: cúbica simples (CS), cúbica de corpo centrado (CCC), cúbica de face centrada (CFC) e hexagonal compacta (HC). Vejamos detalhadamente cada uma delas.

Começando pela estrutura cristalina cúbica simples (CS), cada átomo possui seis átomos vizinhos mais próximos na rede cristalina (Figura 1), ou seja, seu número de coordenação é 6.

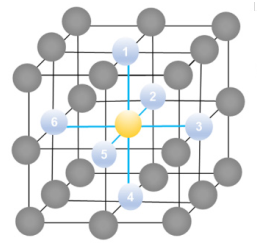
Nessa estrutura, os átomos estão localizados nos vértices do cubo (Figura 2), contribuindo com 1/8 de sua massa total. Como o cubo possui 8 vértices, teremos por célula 1 átomo completo no interior da célula CS. Esse cálculo é expresso por (1).

$nº átomos p/ célula \left(CS\right)=\left(\frac{1}{8}átomo cada vértice\right) x \left(8 vértices\right) = 1 átomo por célula.$

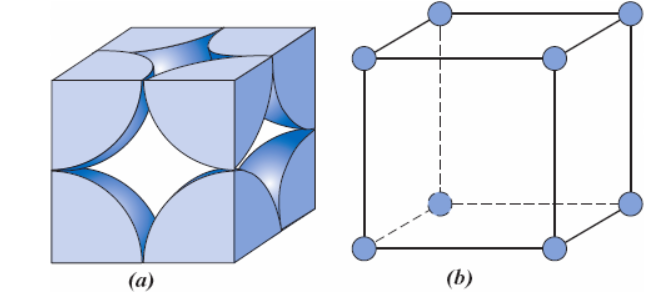
 Em qualquer célula cúbica, a aresta da geometria é denominada de parâmetro de rede, dado pela letra $a$. Esse parâmetro pode ser medido através do raio R dos átomos que constituem a célula cristalina. Com essa informação, é possível calcular o volume da célula cúbica, considerando o volume de um cubo como $V_{cubo} = lad{o}^3$.

Para a célula CS, olhando pela representação da Figura 2, cada aresta é formada pelo raio (R) dos dois átomos que a compõe, logo podemos escrever que $\alpha = 2R$. Assim, para CS, podemos calcular o volume da célula unitária será (2).

$V_{a_{CS}} = {\alpha }^3 = {\left(2R\right)}^3 = 8R^3$

Para analisar a estrutura cristalina, é importante conhecer o valor do Fator de Empacotamento Atômico (FEA) que ela possui, ou seja, quanto do volume da célula é ocupada por átomos. O número do FEA expressa a soma dos volumes das esferas de todos os átomos no interior de uma célula unitária (assumindo o modelo atômico de esferas rígidas) dividida pelo volume da célula unitária. Matematicamente, podemos escrever por (3).

$FEA = \frac{\left(nº átomos por célula\right)\left(volume de cada átomo\right)}{volume da célula unitária}$

Tanto o volume dos átomos quanto o volume da célula unitária podem ser calculados em função do raio atômico R, já que se trata do mesmo elemento químico. E, considerando o átomo como uma esfera, seu volume $\left(V_e\right)$ pode ser calculado por $V_e = \frac{4}{3} \pi R^3$. Logo, aplicando os dados em (3), teremos o FEA para CS por (4).

$FE{A}_{CS} = \frac{\left(nº átomos por celula\right)\left(volume de cada átomo\right)}{volume da célula unitária} = \frac{1\left(\frac{4}{3}\pi R^3\right)}{\left(8R^3\right)} = 52\%$

 

O único elemento que se cristaliza em uma célula unitária cúbica simples é o polônio (Po), elemento radioativo e extremamente tóxico. A razão pela qual os metais não se cristalizam nessa estrutura é devido ao ineficiente empacotamento atômico, já que somente 52% do seu volume total é preenchido. 

Contudo, há uma maneira bastante eficiente de estrutura cristalina, levando em consideração o empacotamento atômico, que é muito encontrada nos metais: a estrutura cristalina cúbica de face centrada (CFC), que apresenta número de coordenação 12. Uma representação dessa estrutura é mostrada através da Figura 3. 

 

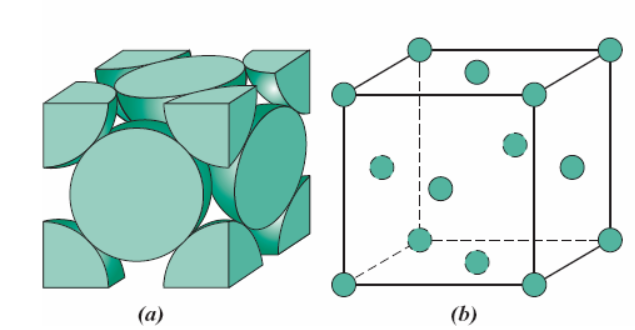
Nesse tipo de estrutura, os átomos estão localizados nos vértices, contribuindo com 1/8 de sua massa total e, em cada face do cubo, há um átomo contribuindo com 1/2 de sua massa total. Assim, o número de átomos por célula na estrutura CFC pode ser calculado por (5).

$nº átomos célula \left(CFC\right) = \left(\frac{1}{8}átomo vértice\right) \left(8vértices\right)+\left(\frac{1}{2}átomo face\right)\left(6 faces\right) = 4 átomo por célula$

Ou seja, são 4 átomos inteiros em cada célula unitária do tipo CFC. Para o cálculo do parâmetro de rede $a$ para a célula cristalina CFC, é preciso verificar a diagonal da face do cubo, local em que átomos se tocam uns nos outros. Através dessa análise, considerando o lado $a$ e os raios R de cada átomo, o comprimento da aresta do cubo a e o raio atômico R estão relacionados por (6).

$\alpha =2R\sqrt{2}$

Com o valor do parâmetro de rede, podemos aplicar (3) e calcular o FEA, que nesse caso terá um valor de 74%, ou seja, apresenta 74% de seu volume total é preenchido. O alumínio, o cobre, a prata e o ouro são alguns dos metais que apresentam estruturas cristalinas CFC.

Além da estrutura cristalina CS e CFC, existe outra estrutura cristalina bastante encontrada nos metais. Essa estrutura também possui célula unitária cúbica, apresentando número de coordenação igual a 8 (Figura 4). Estamos falando da estrutura cúbica de corpo centrado (CCC).

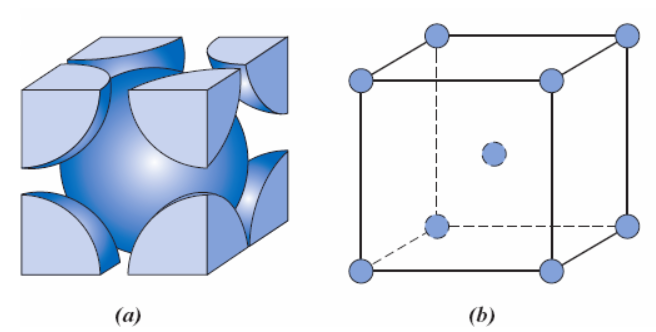
Nessa estrutura, os átomos localizados nos oito vértices contribuem com 1/8 de sua massa total e existe um único átomo inteiro no centro do cubo. Seu número de átomos por célula pode ser calculado por (7).

$nº átomos célula \left(CeC\right) = \left(\frac{1}{8}átomo vétice\right)\left(8 vértices\right)+\left(1 átomo centro\right)= 2 átomos por célula$

Ou seja, são 2 átomos inteiros em cada célula unitária do tipo CCC. Para o cálculo do parâmetro de rede $a$ para a célula cristalina CCC, é preciso verificar a diagonal do cubo, local em que átomos se tocam uns nos outros. Através dessa análise, considerando o lado $a$e os raios R de cada átomo, o comprimento da aresta do cubo a e o raio atômico R estão relacionados por (8).

$\alpha =\frac{4R}{\sqrt{3}}$

Com o valor do parâmetro de rede, podemos aplicar (3) e calcular o FEA, que nesse caso terá um valor de 68%, ou seja, apresenta 68% de seu volume total é preenchido. Como exemplo, o cromo, o ferro e o tungstênio exibem uma estrutura CCC.

Contudo, nem todos os metais possuem células unitárias com simetria cúbico. Existem materiais metálicos que se organizam em uma estrutura cristalina hexagonal. A Figura 5a mostra uma célula unitária com esferas reduzidas para essa estrutura, que é chamada de hexagonal compacta (HC).

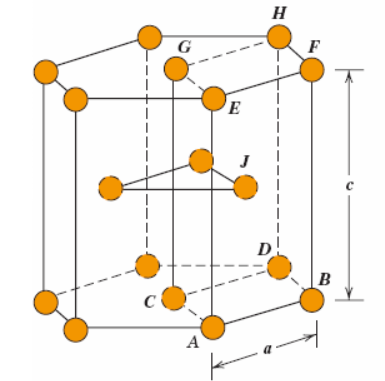
 As faces superior e inferior da célula unitária HC são compostas por seis átomos, que formam hexágonos regulares e envolvem um único átomo central. Outro plano, que contribui com três átomos adicionais para a célula unitária, está localizado entre os planos superior e inferior. Os átomos nesse plano intermediário possuem como vizinhos mais próximos os átomos nos dois planos adjacentes.

O número de átomos por célula em uma estrutura cristalina do tipo HC é calculado considerando um sexto de cada átomo em um vértice na face superior e inferior (para um total de 12 átomos em vértices), 2 átomos nos centros de faces (um em cada uma das faces superior e inferior) e 3 átomos interiores no plano intermediário, totalizando 6 átomos por célula HC.

E ainda, nas estruturas HC temos os parâmetros “a” e “c” que representam a menor e a maior dimensão da célula unitária, respectivamente. A razão entre eles apresenta valor de 1,633, ou seja $\frac{c}{a} = 1,633$. Contudo, alguns metais HC apresentam um desvio em relação a esse valor ideal da razão dos parâmetros. 

Nessa estrutura cristalina, assim como na CFC, o número de coordenação possui valor de 12 e o fator de empacotamento atômico, 0,74. Dentre os metais HC, temos o cádmio, o magnésio, o titânio e o zinco. 

O conhecimento do tipo de célula unitária e da estrutura cristalina de um sólido possibilita o cálculo da sua massa específica teórica ρ através  de (9). 

$\rho = \frac{nA}{V_e N_A}$

Em que n é o número de átomos em cada célula, A o número da massa atômica, V_c é o volume da célula unitária e N_A a constante de Avogadro, $6,023 x {10}^{23} átomos/mol$.

Alguns materiais, sendo metais ou alguns ametais, podem apresentar mais de um tipo de estrutura cristalina no processo de solidificação. Esse fenômeno é denominado de polimorfismo. Contudo, quando essa situação ocorre em sólidos elementares, temos o nome de alotropia. 
No processo de solidificação, a estrutura cristalina que prevalece depende tanto da temperatura quanto da pressão externa. Um dos exemplos mais conhecidos, desse tema, acontece com carbono. Nesse caso, a grafita é o polimorfo estável sob as condições ambientes, enquanto o diamante é formado sob pressões extremamente elevadas. Outro exemplo é o ferro, que possui uma estrutura cristalina CCC à temperatura ambiente e muda para CFC a 912ºC.  Sendo assim, na maioria das vezes, uma transformação polimórfica causa alteração nos valores de massa específica e outras propriedades.

Siga em Frente...

Sistemas cristalinos

As estruturas de todos os cristais que conhecemos podem ser classificadas de acordo com a simetria das células unitárias, existindo um total de sete tipos fundamentalmente distintos dessas células que diferem nos comprimentos relativos das arestas (a, b e c) e dos ângulos formados entre elas (α, β e γ). Esses parâmetros estão indicados na Figura 6 e são às vezes denominados parâmetros da rede cristalina de uma estrutura cristalina.

 

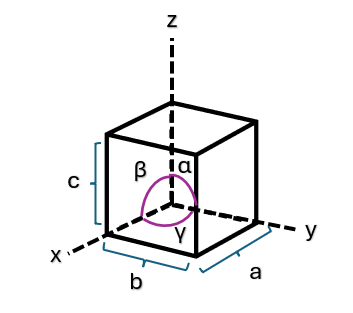
 Com base nesses dados, existem sete possíveis combinações entre os valores de a, b e c e $𝛼$, $𝛽$ e $𝛾$, em que cada combinação é representada por um sistema cristalino distinto. Assim, os arranjos atômicos ou iônicos dos materiais cristalinos podem ser descritos por sete sistemas cristalinos (Figura 7): cúbico, hexagonal, tetragonal, romboédrico (trigonal), ortorrômbico, monoclínico e triclínico. 

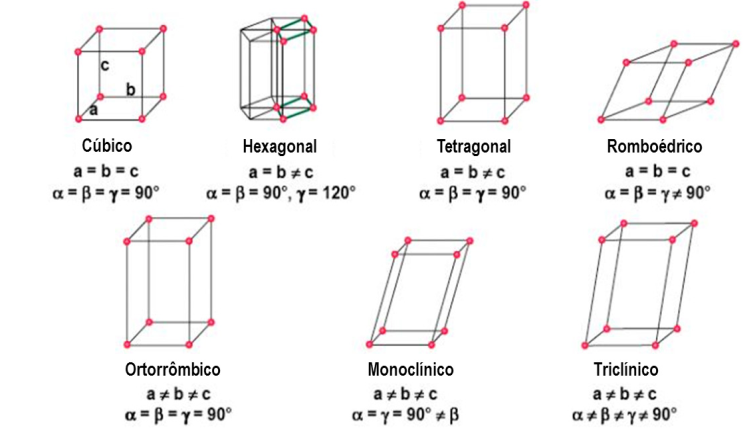
 Entre os sistemas cristalinos, o sistema cúbico é o que apresenta maior grau de simetria, enquanto o sistema triclínico apresenta a menor simetria. Embora existam apenas sete sistemas de cristais ou formas, no total temos 14 redes cristalinas distintas, chamadas rede de Bravais, em homenagem a Auguste Bravais (1811 – 1863), um dos primeiros cristalógrafos francês. A rede de Bravais é composta pelas seguintes redes cristalinas: três tipos cúbicos, um tipo romboédrico, quatro tipos ortorrômbicos, dois tipos tetragonais, um tipo hexagonal, um tipo triclínico e dois tipos monoclínicos (Figura 8).

 

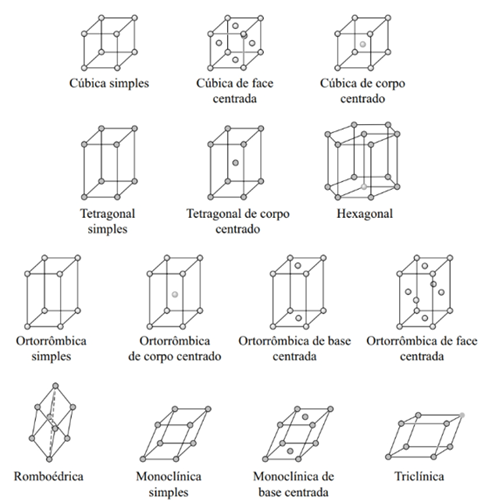
 Na prática, todos os cristais apresentam um desses tipos de sistemas cristalinos. No entanto, alguns compostos que possuem o mesmo sistema podem apresentar diferentes parâmetros de redes, fatores que dependem da composição química e dos tamanhos dos átomos na célula unitária.

Vamos Exercitar?

Relembrando o problema proposto inicialmente, foi solicitado que você realizasse uma pesquisa quanto o ordenamento atômico do ródio, informando qual a estrutura cristalina que possui, o valor do parâmetro de rede, volume e FEA. Por fim, calcular a massa específica para esse material.

No início de sua pesquisa, você descobriu que, através dos dados da tabela periódica, o ródio é um elemento químico de símbolo Rh com Z = 45 e massa atômica igual a 102,9g. E em temperatura ambiente, o ródio encontra-se no estado sólido com ordenamento atômico cristalino, do tipo cúbica de face centrada (CFC).

Nesse tipo de estrutura cristalina, temos 1/8 de átomo em cada vértice e meio átomo no centro de cada face, totalizando 4 átomos por célula cristalina unitária, conforme Figura 9.

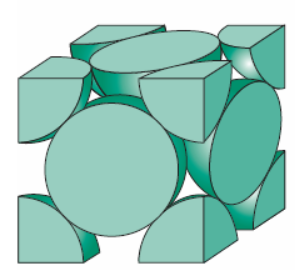
 Conhecendo o tipo de estrutura cristalina, é possível calcular o parâmetro de rede e o volume da célula unitária, ambos em função do raio atômico R. No caso da célula unitária do tipo CFC, olhando para a face cúbica da célula, os átomos se tocam ao longo da diagonal, com comprimento 4R (Figura 10).

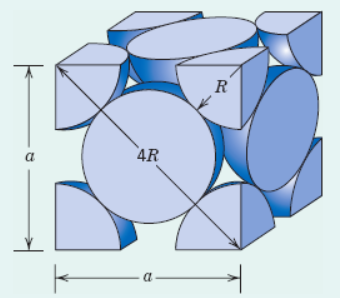
Dessa forma, aplicando o teorema de Pitágoras no triângulo retângulo formado na face do cubo, podemos calcular o parâmetro de rede $a$ por (10).

$a^2 + a^2 = {\left(4R\right)}^2$

A resolução de (10) para obter o parâmetro de rede $a$ para estrutura cristalina do tipo CFC é dado por (11).

$\left.\begin{array}{c}{a}^2 + a^2 = {\left(4R\right)}^2\\ 2a^2 = 16R^2\\ a = 2R\sqrt{2}\end{array}\right\}$

O parâmetro de rede $a$ indica o tamanho da aresta de um cubo. Com esse valor encontrado, podemos calcular o volume por (12).

$\left.\begin{array}{c}V = a.a.a = a^3\\ V = {\left(2R\sqrt{2}\right)}^3\\ V = 16R^3\sqrt{2}\end{array}\right\}$

O próximo passo, consiste em calcular o fator de empacotamento atômico (FEA) para a estrutura CFC. Esse cálculo contempla os valores da quantidade de átomos em cada célula e o volume de cada átomo em função do volume da célula unitária. Assim, o desenvolvimento para o cálculo do FEA é dado por (3).

Tanto o volume dos átomos quanto o volume da célula unitária podem ser calculados em função do raio atômico R, já que se trata do mesmo elemento químico. E, considerando o átomo como uma esfera, seu volume $\left(V_e\right)$ pode ser calculado por $V_e = \frac{4}{3}\pi R^3$. Logo, aplicando os dados em (3), teremos o FEA para CFC por (13).

$FEA = \frac{\left(nº átomos por célula\right)\left(volume de cada átomo\right)}{volume da célula unitária} = \frac{4\left(\frac{4}{3}\pi R^3\right)}{16R^3\sqrt{2}}=0,74$

Esse valor indica que 74% do volume da célula unitária está ocupado por átomos. 

Por fim, é necessário calcula a massa específica do ródio. Para isso, precisamos de alguns valores buscados na literatura: raio atômico (R) de 0,134nm, estrutura cristalina CFC e massa atômica (A) de 102,91g/mol. Lembrando que a estrutura cristalina do tipo CFC possui 4 átomos por célula (n) e volume da célula (V_c) de $16R^3\sqrt{2}$, teremos a massa específica $𝜌$ desse elemento dada por (14). Importante atenção com as unidades das grandezas.

$p = \frac{nA}{V_c N_A} = \frac{\left(4 átomos/célula\right)\left(102,91 g/mol\right)}{\left[16{\left(1,34 x {10}^{-8}cm\right)}^3\sqrt{2}\right]\left(6,023x{10}^{23}átomos/mol\right)}=12,55\frac{g}{c{m}^3}$

Assim, todas as informações a respeito do elemento e seu tipo de estrutura cristalina foram obtidas.

Saiba Mais

Olá, Estudante!

Compreender como os átomos se organizam em uma estrutura cristalina, por muitas vezes, não é algo tão trivial. Dessa forma, com o objetivo de facilitar essa visualização, acesse o Software CrystalWalk, um programa interativo que revela estrutura de cristais para melhor compreensão dos estudantes. É de acesso gratuito com a possibilidade de construir cristais passo a passo e ver sua estrutura em imagens tridimensionais. Dessa forma, acesse o link abaixo, construa as estruturas cristalinas que desejar. Isso ajudará a trazer melhor compreensão sobre o assunto.

Bons estudos!

Referências Bibliográficas

ASKELAND, Donald R.; WRIGHT, Wendelin J. Ciência e engenharia dos materiais – Tradução da 4a edição norte-americana. São Paulo: Cengage Learning Brasil, 2019. E-book. ISBN 9788522128129. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128129/. Acesso em: 02 abr. 2024.

JR., William D C. Ciência e Engenharia de Materiais - Uma Introdução. Rio de Janeiro: Grupo GEN, 2020. E-book. ISBN 9788521637325. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521637325/. Acesso em: 02 abr. 2024.

NEWELL, James. Fundamentos da Moderna Engenharia e Ciência dos Materiais. Rio de Janeiro: Grupo GEN, 2010. E-book. ISBN 978-85-216-2490-5. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/978-85-216-2490-5/. Acesso em: 02 abr. 2024.

SMITH, William F.; HASHEMI, Javad. Fundamentos de Engenharia e Ciência dos Materiais. Porto Alegre: Grupo A, 2012. E-book. ISBN 9788580551150. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788580551150/. Acesso em: 02 abr. 2024.

Pontos, direções e planos cristalogáficos

Olá, Estudante! Nessa videoaula veremos os conceitos relacionados aos pontos, direções e planos Cristalográficos. Vamos compreender como obter esses valores e como, a partir deles, realizar sua descrição em uma célula cristalina.

Esse tema é importante para o desenvolvimento de sua prática profissional, já essas informações em sólidos cristalinos estão diretamente relacionadas com algumas propriedades apresentadas pelos materiais.

Vamos juntos buscar a localização de pontos, direções e planos em sistemas através de análises cristalográficas?!

Bons estudos!!!

Ponto de Partida

Olá, Estudante! Como está?!

Nessa aula falaremos sobre os conceitos que permeiam a cristalografia. E o que é a cristalografia? É a ciência que estuda a disposição dos átomos em sólidos cristalinos. Assim, o objetivo dessa aula consiste em entender como identificar e obter os pontos, coordenadas, direções e planos em estruturas cristalinas.

Esse tema é de extrema importância para sua formação na área pelo fato de que a estrutura cristalina está diretamente relacionada às propriedades apresentadas pelos materiais. Logo, compreender como os elementos estão dispostos nos materiais, direções e planos nas células cristalinas ajudarão a analisar o material e verificar, segundo as propriedades e o direcionamento dos crescimentos de grãos, quais as características mais marcantes do material e como ele pode ser mais bem utilizado no desenvolvimento dos projetos.

Sendo assim, considere uma situação em que você, atuando como estagiário em um laboratório de caracterização óptica de materiais, se depara com um relatório de um conjunto de medidas de um material hipotético. Nesse relatório, consta gráficos realizados com dados de direções e planos cristalográficos de uma estrutura cristalina cúbica. Dessa forma, seu orientador solicitou que você obtivesse os índices de Miller para as direções e planos contidas no relatório. 

Para isso, as direções cristalográficas que deverão ser avaliadas estão apresentadas na estrutura cristalina cúbica da Figura 1a. Já os planos cristalográficos, na estrutura cristalina cúbica da Figura 1b.

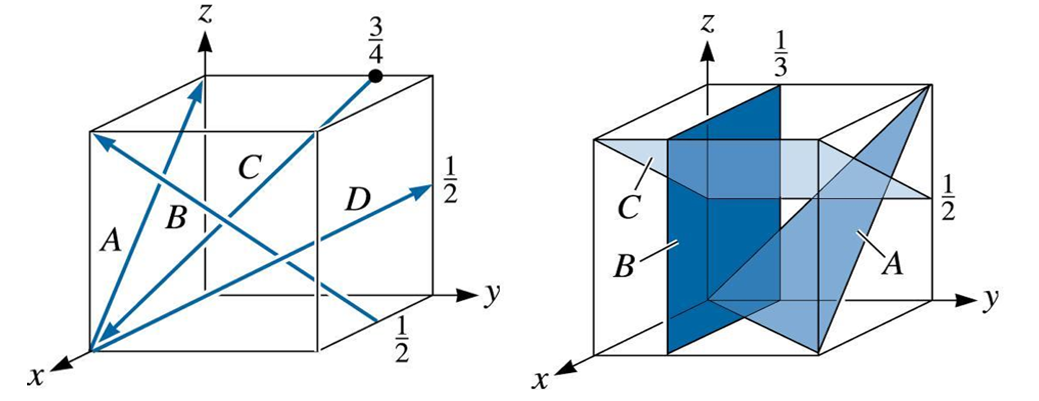
Ao final dos cálculos, os índices de Miller para cada direção e plano deve ser acrescentado no relatório do conjunto de medidas que foi analisado. 

Como o assunto é de grande importância para a formação de um bom profissional da área, vamos conhecer os conceitos necessários para resolução do problema proposto?

Bons estudos!

Vamos Começar!

Coordenadas dos pontos

Normalmente é necessário especificar um ponto, uma direção ou um plano no estudo da cristalografia dos átomos, já que algumas propriedades como deformação que um material apresenta sob carga, condutividade elétrica e térmica e módulo de elasticidade podem variar de acordo com a orientação do cristal de um material sólido.

A localização de átomos ou a posição de qualquer ponto dentro da célula unitária pode ser especificada utilizando coordenadas cartesianas na forma de múltiplos fracionários dos comprimentos das arestas que a célula unitária possui. Para isso, basta alocar o pronto principal da célula sob a origem de um sistema cartesiano e verificar a distância dos pontos em análise com a origem, levando em consideração o tamanho de aresta da célula cristalina igual a um.

Ou seja, a distância é medida levando pelo número de parâmetros de rede que é preciso mover em cada uma das coordenadas x, y e z para ir da origem 0, 0, 0 ao ponto em questão. E ainda, para expressá-las, as coordenadas são dadas como três distâncias separadas por vírgulas na ordem x, y, z. A Figura 2 apresenta uma célula unitária cúbica com alguns exemplos de coordenadas de pontos em seu interior, assumindo unidade de aresta igual a 1, em que cada conjunto de números se refere à distância do ponto em relação à origem, quanto aos parâmetros de rede.

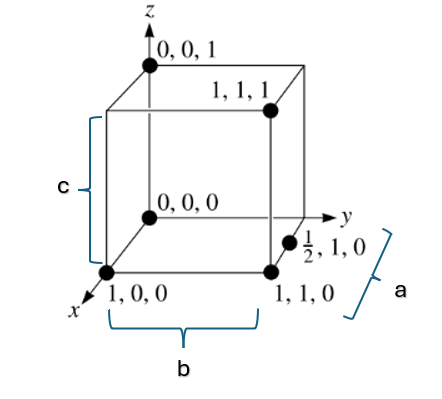
 Como exemplo, vamos analisar a estrutura cristalina apresentada pela Figura 3. Ela é do tipo cúbica de corpo centrada (CCC) e podemos obter a localização dos átomos nessa célula através de suas coordenadas.

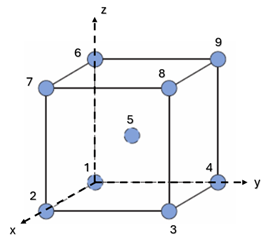
 Assim, pela Figura 3, assumindo unidade de aresta igual a 1 e que a origem do sistema cartesiano está localizada no ponto 1, teremos as coordenadas de cada átomo dada por:

• 0, 0, 0 para o ponto 1;
• 1, 0, 0 para o ponto 2;
• 1, 1, 0 para o ponto 3;
• 0, 1, 0 para o ponto 4;
• ½, ½, ½ para o ponto 5;
• 0, 0, 1 para o ponto 6;
• 1, 0, 1 para o ponto 7;
• 1, 1, 1 para o ponto 8;
• 0, 1, 1 para o ponto 9.

Esses serão os índices para os 9 pontos indicados na célula unitária da Figura 2. Repare no ponto 5, ele expressa o valor ½, indicando que o ponto está localizado no meio da aresta. Ou seja, esse processo não contempla apenas a representação de pontos com números inteiros, mas suas frações também.

Direções cristalográficas

Uma direção cristalográfica é definida como uma linha direcionada entre dois pontos, também denominada de vetor. As seguintes etapas são usadas para determinar os três índices direcionais:

• Primeiro, através de um sistema de coordenadas orientadas, é necessário determinar as coordenadas de dois pontos alocados na direção em estudo.
• Com as coordenadas desses dois pontos, subtraia as coordenadas do ponto final das coordenadas do ponto inicial, a fim de obter o número de parâmetros de rede percorridos na direção de cada eixo do sistema de coordenadas.
• Próximo passo consiste em eliminar as frações por meio de divisão/multiplicação dos resultados da subtração para obter os menores números inteiros possíveis. Ou seja, esses três números devem ser multiplicados ou divididos por um fator comum para reduzi-los aos menores valores inteiros, quando necessário.
• Assim, os índices obtidos devem ser colocados entre colchetes [$uvw$]. Caso haja algum sinal negativo, represente-o com uma barra sobre o número. Os números inteiros u, v e w correspondem às diferenças de coordenadas normalizadas com referência aos eixos x, y e z, respectivamente.

Olhando para o sistema de coordenadas, para cada um dos três eixos (x, y e z) existirão tanto coordenadas positivas quanto negativas. Por essa razão, também são possíveis índices negativos, que deverão ser representados por uma barra sobre o índice apropriado, como dito anteriormente. Por exemplo, a direção $\left[\overline{111}\right]$ apresenta um componente negativo na direção y. 

E ainda, a mudança dos sinais de todos os índices produz uma direção antiparalela, ou seja, a direção $\left[\overline{111}\right]$ é diretamente oposta à direção $\left[\overline{111}\right]$.

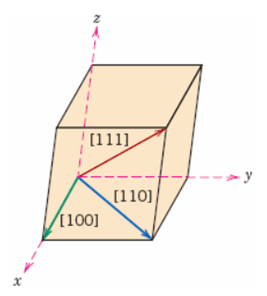
Como exemplo, vejamos as direções [100] [110] e [111] em uma célula unitária do tipo cúbica, apresentadas pela Figura 4.  

Para fixar os conteúdos, vamos determinar as direções A, B e C contidas em uma estrutura cristalina tipo cúbica, representada pela Figura 5, aplicando o passo a passo para obter os índices em cada direção. 

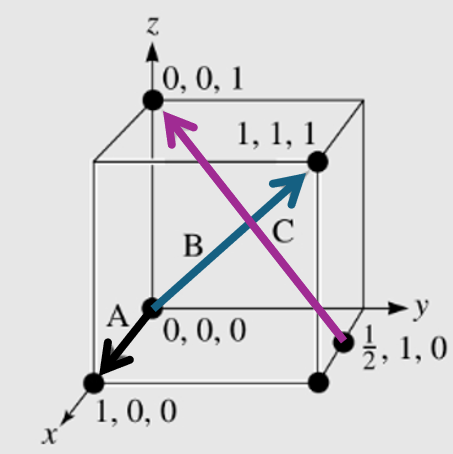
 Para isso, vamos começar com a direção A. Pela Figura 5, vemos que a direção A sai da coordenada 0, 0, 0 e chega na coordenada 1, 0, 0. Agora, precisamos subtrair as coordenadas do ponto final das coordenadas do ponto inicial: 1, 0, 0 – 0, 0, 0 = 1, 0, 0$1, 0, 0 – 0, 0, 0 = 1, 0, 0$. Nesse caso, não é preciso eliminar as frações, por não há, e nem reduzir os números inteiros. Por fim, a direção A é dada por [100].

A mesma análise vamos fazer para a direção B. As coordenadas inicial e final são, respectivamente 0, 0, 0 e 1, 1, 1. Realizando a subtração:

1, 1, 1 – 0, 0, 0 = 1, 1, 1$1, 1, 1 – 0, 0, 0 = 1, 1, 1$. Por fim, como não há frações e nem números negativos, a direção B é dada por $\left[111\right]$. 

Por fim, para direção C, os dois pontos são: ½, 1, 0 e 0, 0, 1 (inicial e final, respectivamente). Realizando a subtração: $0, 0, 1-\frac{1}{2}, 1, 0 = -\frac{1}{2},-1, 1.$ Nesse caso, temos uma fração (1/2) e para reduzi-la a um número inteiro, basta multiplicar o resultado por 2. Assim: $2\left(-\frac{1}{2}, -1, 1\right)= -1, -2, 2.$ Como não há possibilidade de redução dos índices, a direção C é dada por $\left[\overline{)1} \overline{)2} 2\right]$.

Os números das direções são denominados de índices de Miller de direção. Para esses índices, alguns aspectos a respeito de sua utilização precisam ser analisados. Dentre eles:

• Como as direções são vetores, determinada direção e seu negativo não são idênticos. Por exemplo: [100] não equivale a $\left[\overline{1} 00\right]$ eles representam a mesma linha, mas possuem sentidos opostos.
• Os múltiplos são idênticos às direções. Por exemplo, $\left[100\right]$ representa a mesma direção que $\left[200\right]$.
• Alguns grupos de direções são equivalentes, pois possuem índices específicos em função de como a coordenada é construída. Por exemplo, no sistema cúbico uma direção $\left[100\right]$ será a direção $\left[010\right]$ se o sistema de coordenadas for ajustado, ou seja, modificado (Figura 6).

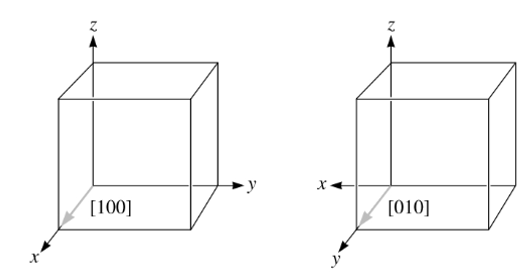
 Os grupos de direções equivalentes podem ser chamados de famílias de direções, utilizando os símbolos $< >$para indicar o conjunto de direções. Como exemplo, vejamos família de direções $<110>$ expressa por (1).

$< 110 > = \left\{\begin{array}{c}\left[110\right] \left[\overline{)1} \overline{)1} 0\right]\\ \left[101\right] \left[\overline{1} 0 \overline{1}\right]\\ \left[011\right] \left[0 \overline{1} \overline{1}\right]\\ \left[1 \overline{)1} 0\right] \left[\overline{)1} 10\right]\\ \left[10\overline{1}\right] \left[\overline{1} 01\right]\\ \left[01\overline{1}\right] \left[0 \overline{1} 1\right]\end{array}\right.$

As direções cristalográficas são utilizadas para determinar a orientação de um cristal, seja do tipo mono ou poli cristal. Saber como realizar essa descrição é muito útil em diversas aplicações, por exemplo: com relação aos materiais metálicos, eles se deformam com mais facilidade em direções que os átomos estão em contato mais próximo.

Siga em Frente...

Planos cristalográficos 

Assim como as direções, os planos cristalográficos podem ser representados através de índices de Miller. Para isso, é considerado uma célula unitária como base em um sistema de coordenadas (x, y e z). Importante ressaltar que, com exceção ao sistema cristalino hexagonal, todos os sistemas cristalinos os planos cristalográficos são representados pelos índices de Miller na forma $\left(hkl\right)$, em que quaisquer dois planos paralelos entre si são equivalentes e possuem índices idênticos.

Para determinar os índices $hkl$, será necessário:

• Identificar os pontos em que os planos interceptam os eixos x, y e z considerando o número de parâmetros de rede. Atenção: se o plano passar pela origem, a origem das coordenadas deverá ser deslocada para a de uma célula unitária adjacente.
• Calcular os inversos dessas intersecções.
• Eliminar as frações, mas sem arredondar para os números inteiros mais baixos.

Colocar os números resultantes entre parênteses ( ). Observe: os índices negativos devem ser expressos com uma barra sobreposta, análogo feito nas direções. Não são utilizadas vírgulas para separar os índices.

Como exemplo para obter os índices de Miller dos planos, observe a Figura 7. Ela apresenta dois planos distintos em uma célula cristalina, um retangular (a) e outro triangular (b). Para encontrar os planos cristalográficos de cada plano, vamos considerar aresta de tamanho 1 para a célula cúbica.

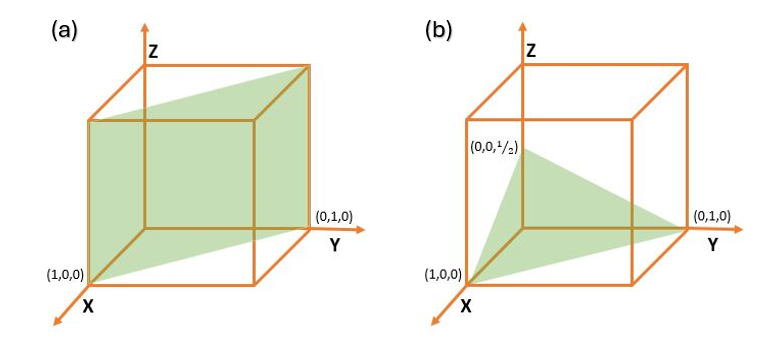
Para o plano representado pela Figura 7a, primeiro vamos identificar os pontos em que os planos interceptam os eixos x, y e z. Nesse caso, há interseção apenas em x = 1$x = 1$e y = 1$y = 1$. No eixo z, o plano é paralelo ao eixo e, nesse caso, consideramos que a interseção acontecerá no infinito, ou seja, $z =$∞. Feito isso, precisamos calcular os inversos, ou seja $\frac{1}{x} = 1 \frac{1}{y} = 1 e \frac{1}{z} = \frac{1}{\infty } = 0.$ Como não há frações para eliminar, podemos escrever os índices de Miller para esse plano por (110).

Já para o plano representado pela Figura 7b, os pontos em que os planos interceptam os eixos x, y e z são 1, 1 e ½, respectivamente. Agora, é necessário calcular os inversos, ou seja $\frac{1}{x} = 1; e \frac{1}{z}=2.$

Como não há frações para eliminar, podemos escrever os índices de Miller para esse plano por (112).

Por fim, alguns aspectos são importantes com relação aos índices de Miller para os planos. São eles:

• Os planos e seus respectivos negativos são idênticos pelo fato de serem paralelos. Com isso, $\left(020\right) = \left(0\overline{)2}0\right)$.

Os planos não são idênticos a seus múltiplos. 

• Em cada célula unitária, uma família de planos representa grupos de planos equivalentes. Esses planos têm índices similares e representamos esses grupos de planos similares com a notação {}. Vejamos os planos na forma {110} para os sistemas cúbicos por (2).

$\left\{110\right\} = \left\{\begin{array}{c}\left(110\right)\\ \left(101\right)\\ \left(011\right)\\ \left(1\overline{)1}0\right)\\ \left(10\overline{)1}\right)\\ \left(01\overline{)1}\right)\end{array}\right.$

• Para os sistemas cúbicos, uma direção com os mesmos índices de um plano é perpendicular a esse plano.

Até agora, vimos situações em que obtemos os valores para os índices das direções e dos planos cristalográficos. Contudo, o inverso pode ser realizado também, ou seja, podemos obter a direção ou plano através de seus índices. Para isso, para construir uma direção ou um plano na célula unitária basta realizar o procedimento inverso.

Como exemplo, vamos desenhar a direção $\left[101\right]$ e o plano ($\stackrel{-}{2}10$) em uma célula unitária cúbica. Assim, começando pela direção, basta desenharmos uma célula unitária cúbica com a sua base na origem do sistema cartesiano e encontrar a coordenada 1, 0, 1. Feito isso, traçar a reta unindo a origem até a coordenada (Figura 8a). Já para o plano, temos que $\frac{1}{x} = -2 e \frac{1}{z}=0.$ Logo, teremos que $x = -\frac{1}{2}; y= 1 e z = \infty$ (Figura 8b). Não podemos esquecer de que, quando desenhar a estrutura cristalina, o plano não pode passar pela origem, caso ocorra, a origem das coordenadas deverá ser deslocada para a de uma célula unitária adjacente. Nesse caso, foi transladado para frente no eixo x, local onde está a bolinha verde.

 

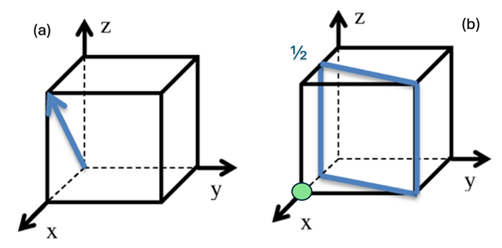
Importante destacar que, em cristais cúbicos, os planos e direções com índices iguais são perpendiculares entre si. Contudo, para os demais sistemas cristalinos não há relações geométricas simples entre planos e direções com índices iguais.

Vamos Exercitar?

$\left[4\overline{)3} \overline{)4}\right]$ 0, Relembrando o problema proposto inicialmente, você é estagiário em um laboratório de caracterização óptica de materiais e precisa obter os índices de Miller para as direções e planos contidas no relatório de uma amostra específica. Para isso, foi disponibilizado as estruturas cristalinas do tipo cúbica com as direções e planos a serem definidos (Figura 1).

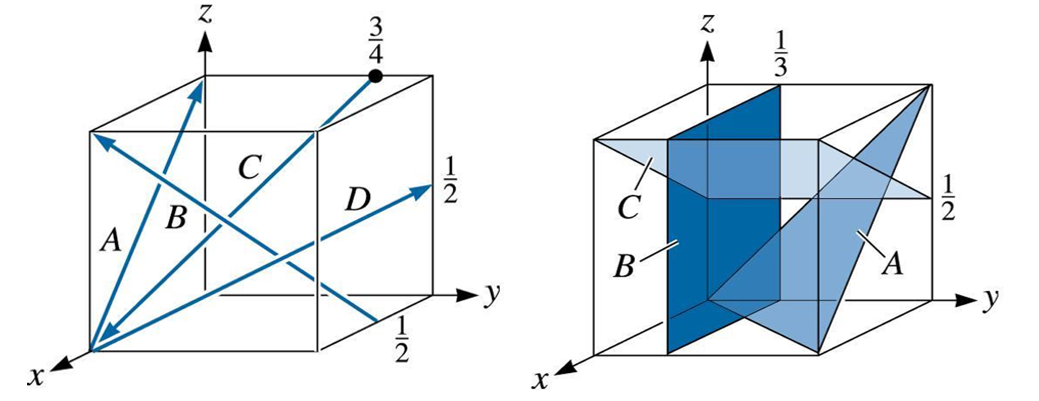
 Vamos começar a análise dos índices de Miller das 4 direções apresentadas na estrutura cristalina cúbica (Figura 1a). Assim, olhando para cada direção separadamente:

• Direção A: coordenada inicial $1, 0, 0$ e coordenada final $0, 0, 1$. Assim, a subtração da coordenada final menos a inicial é dada por $0, 0, 1-1, 0, 0=-1, 0,1$. Como não há frações e nem reduções possíveis, a direção A será $\left[\overline{)1}01\right]$.
• Direção B. Vamos seguir o mesmo raciocínio da direção A. Coordenadas inicial e final, respectivamente, $½, 1, 0$ e 1, 0, 1.  A subtração será $1, 0, 1 -\frac{1}{2}, 1, 0 = \frac{1}{2}, -1, 1.$ Como existe uma fração, vamos multiplicar todos os índices da direção por 2, logo teremos $2\left(\frac{1}{2}, -1,1\right)=1, -2, 2.$ Assim, a direção B é definida por $\left[1\overline{)2}2\right]$.
• Direção C, seguindo os passos anteriores, será dada por $\left[4\overline{)3} \overline{)4}\right]$.
• Direção D igual a $\left[\overline{)2} 21\right]$.

Agora será necessário obter os índices para os planos cristalográficos (Figura 1b). Olhando para cada plano separadamente, teremos: 

• Plano A: como o plano intercepta a origem do sistema de coordenadas, vamos transladar a origem do sistema uma unidade no eixo y. Assim, para o novo sistema de coordenadas, o plano intercepta os eixos em $x=1, y= -1 e z = 1.$ Verificando seus valores inversos, teremos $\frac{1}{x} = 1, \frac{1}{y} = -1 e \frac{1}{z} = 1.$ Como não temos frações e nem redução de números, o plano A é dado por $\left(1\overline{)1}1\right)$.
• Plano B: esse plano intercepta apenas o eixo y. Assim, os pontos serão $x = \infty , y=\frac{1}{3} e z=\infty .$ Considerando o inverso dos pontos, $\frac{1}{x} = 0, \frac{1}{y} = 3 e \frac{1}{z} = 0.$ Como não há frações e nem possibilidade de redução, o plano B será $\left(030\right)$.
• Plano C: para esse plano, podemos transladar o sistema de coordenadas subindo uma unidade em z. Assim, no novo sistema de coordenadas, o plano interceptará os eixos em $x = 1, y= \infty e z = \frac{-1}{2}.$ Logo, fazendo as etapas necessárias, o plano C é dado por $\left(10\overline{)2}\right).$

Assim, com esses cálculos e análises, obtemos os índices de Miller para as direções e planos dados.

  

 

 

Saiba Mais

Olá, Estudante! 

Aprofunde seus conhecimentos a respeito da estrutura em sólidos cristalinos, bem como análise e obtenção de Pontos, Direções e Planos Cristalográficos lendo o Capítulo 3 do livro Ciência e Engenharia de Materiais do autor Callister. Estude os conceitos, veja os exemplos e faça os exercícios.

JR., William D C. Ciência e Engenharia de Materiais - Uma Introdução. Rio de Janeiro: Grupo GEN, 2020. E-book. ISBN 9788521637325.

Bons estudos!

Referências Bibliográficas

ASKELAND, Donald R.; WRIGHT, Wendelin J. Ciência e engenharia dos materiais – Tradução da 4a edição norte-americana. São Paulo: Cengage Learning Brasil, 2019. E-book. ISBN 9788522128129. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128129/. Acesso em: 04 abr. 2024.

JR., William D C. Ciência e Engenharia de Materiais - Uma Introdução. Rio de Janeiro: Grupo GEN, 2020. E-book. ISBN 9788521637325. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521637325/. Acesso em: 04 abr. 2024.

NEWELL, James. Fundamentos da Moderna Engenharia e Ciência dos Materiais. Rio de Janeiro: Grupo GEN, 2010. E-book. ISBN 978-85-216-2490-5. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/978-85-216-2490-5/. Acesso em: 04 abr. 2024.

SMITH, William F.; HASHEMI, Javad. Fundamentos de Engenharia e Ciência dos Materiais. Porto Alegre: Grupo A, 2012. E-book. ISBN 9788580551150. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788580551150/. Acesso em: 04 abr. 2024.

Imperfeições cristalinas

Olá, Estudante! Nessa videoaula iremos estudar sobre as imperfeições nos sólidos, isto é, os defeitos contidos nos materiais sólidos. Com isso, vamos compreender quão importante é a presença desses defeitos nos materiais e como eles estão associados com as propriedades dos materiais.

Se não existissem os defeitos, os cristais não teriam cores, não existiriam os dispositivos eletrônicos do estado sólido e alguns metais seriam tão resistentes que não poderiam ser utilizados. É por essa razão que esse tema é muito importante para o desenvolvimento de sua prática pessoal, acadêmica e profissional.

Pronto para compreender o que são imperfeições cristalinas e como estão relacionadas com as propriedades dos materiais?!

Vamos lá!!!

Ponto de Partida

Olá, Estudante!

Nessa aula vamos abordar os conceitos relacionados às imperfeições cristalinas, ou seja, defeitos que podem existir em estruturas cristalinas de um material sólido. Quando falamos em imperfeições, defeitos, parece ser algo ruim e de má qualidade. Contudo, com uma visão microscópica atenta ao ordenamento atômico em arranjos que se repetem, esses defeitos são fundamentais para que o material sólido seja termodinamicamente estável. E ainda, o tipo de imperfeição impacta diretamente nas propriedades físicas e mecânicas da estrutura.

Dessa forma, para compreensão desse tema, vamos entender o que são defeitos pontuais, como eles se apresentam e quais as consequências para o material. Depois, falaremos dos tipos de imperfeições diversas que podem ser atuantes e como elas se movem pela da rede cristalina do material. E, por fim, discutiremos os mecanismos pelos quais a análise microscópica da estrutura possa ser verificada.

Sobre essa temática, considere uma situação em que você atua como vendedor técnico de uma metalúrgica e está negociando a venda de um lote de ferro α para um cliente bem exigente, que a cada momento apresenta uma nova dúvida. Você sabe que essa venda é muito importante para a metalúrgica, já que a empresa está passando por processo de expansão e precisa aumentar a carteira de clientes e, consequentemente, seus rendimentos.

Foi informado que o cliente em potencial utilizará o ferro α em diversas aplicações e em diferentes condições de temperatura. Pensando nisso, você já esclareceu a ele que o ferro α só apresenta a propriedade de ser ferromagnético em temperaturas inferiores a 771°C e, posteriormente, explicou porque esse metal de estrutura cúbica de corpo centrado é maleável, flexível, de baixa rigidez e as demais propriedades relacionadas com o sistema cristalino que possui.

Assim, pensando em novas aplicações, o cliente questionou se existe a possibilidade de aumentar a dureza do ferro α. Mas como é possível modificar a propriedade mecânica do metal? Os metais apresentam algum tipo de impureza ou defeito? Quais tipos de defeitos o ferro α pode apresentar?

Para responder a esses questionamentos, alguns conceitos são necessários, principalmente para compreender o que são impurezas nos materiais sólidos e como a adição delas, de maneira intencional, pode alterar algumas propriedades iniciais. Vamos lá?! Bons estudos!

Vamos Começar!

 Defeitos pontuais

As estruturas cristalinas apresentadas pelos materiais podem ser idealizadas e simplificadas, de maneira que possam ser utilizadas para compreensão de muitos princípios importantes que regem o comportamento dos sólidos. Contudo, cristais reais apresentam grande número de defeitos (imperfeições), na rede cristalina, que variam desde a quantidade de impurezas até a falta de átomos ou íons. Esses defeitos, ou imperfeições, impactam diretamente nas propriedades dos materiais.

Todos concordam que é comum a palavra “defeito” trazer a sensação de algo ruim ou indesejável. Mas olhando para os materiais, e o estudo a respeito de sua constituição microscópica, os defeitos importantes para a instabilidade termodinâmica do material e são intencionalmente utilizados para manipular as propriedades apresentadas por ele.

Dentre os tipos de defeitos possíveis em sólidos cristalinos, os mais comuns são conhecidos como: defeitos pontuais, defeitos lineares, defeitos interfaciais e defeitos volumétricos.

Os defeitos pontuais são denominados por regiões em que há ausência de um átomo ou o átomo se encontra em uma região irregular na estrutura cristalina. Entre os defeitos pontuais, temos lacunas, autointersticial, impurezas substitucionais e intersticiais. Dentre eles, a lacuna é o defeito mais simples e, como o próprio nome sugere, é dado pela ausência de um átomo na rede cristalina, como mostra a Figura 1.

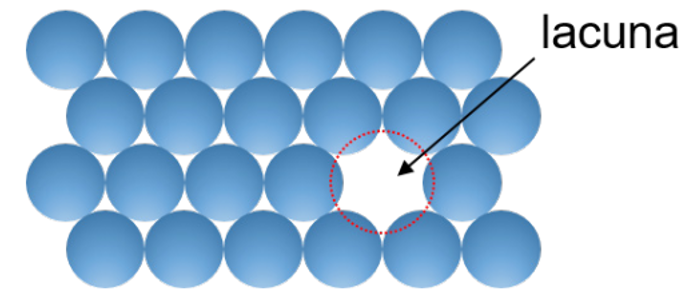
As lacunas são defeitos muito comuns na rede cristalina, especialmente em materiais que estão em altas temperaturas, quando os átomos estão em movimento e mudam de posições na rede aleatoriamente, deixando para trás pontos da rede vazio. O defeito do tipo lacuna também é conhecido como buraco ou vacância e, na realidade, não é possível construir um sólido sem esse tipo de defeito. O processo de difusão é um exemplo da atuação desse tipo de defeito. E ainda, é possível determinar o número de lacunas em uma rede cristalina através de (1).

$N_l = N exp\left(-\frac{Q_l}{kT}\right)$

Em que N é o número total de sítios atômicos vazios (vacâncias), $Q_l$ é a energia necessária para a formação de uma lacuna (vacância), T a temperatura em escala Kelvin e k a constante de Boltzmann, de valor $8,62 x {10}^{-5} e \frac{V}{átomo K}$ $1,38 x {10}^{-23} \frac{J}{átomo K}$ .Já o número total de sítios atômicos pode ser calculado por (2).

$N = \frac{N_{A\rho }}{A}$

Em (2), $N_A$ representa o número de Avogadro, $𝜌$ a massa específica e A o peso atômico. Por ela, vemos que a quantidade de lacunas apresenta um aumento exponencial em função da temperatura.

Para melhor compreensão desse conceito, como exemplo, vamos determinar o número de lacunas no ferro, em 900º, sabendo que a massa específica desse elemento é igual a $7,65 \frac{g}{c{m}^3}$ peso atômico de 55,85 g/mol, número de Avogadro de $6,023 x {10}^{23} átomos/mol$ e energia de formação de uma lacuna de 1,08 eV/átomo.

Para encontrar o valor pedido, partimos de (1) e substituindo N por (2), o cálculo para o número de lacunas, realizando as conversões de unidades necessárias, é expresso por (3).

$\left.\begin{array}{c}{N}_l = exp \left(-\frac{Q_l}{kT}\right)=\frac{N_{A\rho }}{A}exp\left(-\frac{Q_l}{kT}\right)\\ N_l=\frac{\left(6,023 x {10}^{23}\right)\left(7,65\right)}{55,85}exp\left(-\frac{1,08}{\left(8,62 x {10}^{-5}\right)\left(1173K\right)}\right)\\ N_l=1,9 x {10}^{18} lacunas/c{m}^3\end{array}\right\}$

Outro tipo de defeito pontual é conhecido como autointersticial, em que um átomo da rede cristalina se desloca para um sítio intersticial, ficando comprimido naquele local, uma região que, sob condições normais, não estaria ocupada.

Em materiais reais, um metal puro, que é formado apenas por um tipo de átomo, é simplesmente impossível, pois impurezas ou átomos diferentes estão sempre presentes nas estruturas. A adição de átomos em um metal resulta na formação de uma solução sólida, que se forma quando, à medida que os átomos de soluto (em menor quantidade) são adicionados ao material hospedeiro (solvente, em maior quantidade), a estrutura cristalina é mantida e nenhuma estrutura nova é formada, mas esse processo resulta em alteração de propriedades no material. As soluções sólidas podem ser do tipo substitucional ou intersticial, em que:

• As soluções sólidas substitucionais são aquelas em que um átomo, diferente dos que formam a rede cristalina, substitui outro átomo da estrutura. Geralmente, os átomos envolvidos nesse tipo de situação apresentam no máximo 15% do raio do átomo da estrutura original. Como exemplo desse tipo de defeito, temos os átomos de zinco no latão, substituindo alguns átomos de cobre.
• As soluções sólidas intersticiais são aquelas em que átomos muito menores do que os da rede cristalina se encaixam no espaço vazio existente entre os sítios da rede principal. Em uma situação natural, esses elementos não seriam encontrados nesses espaços vazios. Como exemplo desse tipo de defeito, temos os átomos de carbono nos interstícios de ferro, com concentração máxima de carbono de 2% (maior concentração de carbono resulta em alteração na estrutura cristalina inicial do material).

A Figura 2 apresenta os diferentes tipos de defeitos pontuais, considerando as lacunas, autointersticial, solução sólida substitucional (impureza substitucional) e solução sólida intersticial (impureza intersticial).

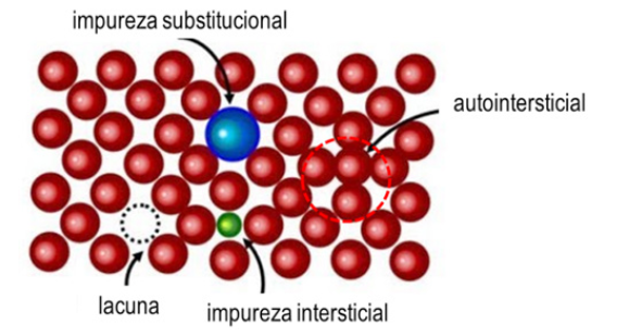
Importante ressaltar que cada um dos defeitos pontuais citados levam em consideração a composição do material, bem como o tipo de estrutura cristalina e o raio dos elementos envolvidos.

Siga em Frente...

Imperfeições diversas

Além dos defeitos pontuais, uma estrutura pode apresentar discordâncias, que são defeitos lineares observados em átomos que estão desalinhados. Ou seja, as discordâncias são defeitos em que alguns átomos se encontram fora da sua posição inicial na estrutura cristalina, em que sua principal função consiste em controlar a resistência ao escoamento e a subsequente deformação plástica dos sólidos cristalinos a temperaturas normais, sem que ocorra transformação de fase.

As discordâncias também participam do crescimento dos cristais e das estruturas de interfaces entre eles e são geradas e movidas quando uma tensão é aplicada. Existem dois tipos básicos de discordâncias: a discordância aresta e a discordância espiral.

A discordância em aresta pode ser facilmente visualizada como um semiplano extra de átomos em uma estrutura cristalina. Muitas vezes esses semiplanos são chamados de linhas da discordância, devido ao alinhamento dos átomos ao longo de uma linha (Figura 3). Na discordância em aresta, as ligações interatômicas são significativamente distorcidas nas imediações da linha de discordância. Compreender o movimento de uma discordância é fundamental para entender a deformação plástica nos materiais, que corresponde ao movimento de grandes números de discordâncias. 

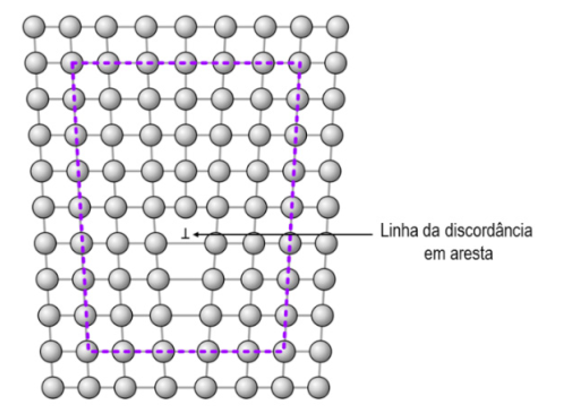
 Uma discordância em aresta se move de forma semelhante a uma lagarta, ou seja, uma pequena quantidade por vez (um sítio por vez). Olhando para Figura 4, que apresenta o movimento de uma discordância no interior de um cristal quando sujeito a uma tensão de cisalhamento, vemos que a discordância na metade superior do cristal está deslizando plano por plano, da esquerda para a direita, iniciando na posição A, passando por B até formar uma unidade de distância interatômica à direita do cristal. Assim, uma pequena fração das ligações interatômicas são quebradas durante o movimento da discordância.

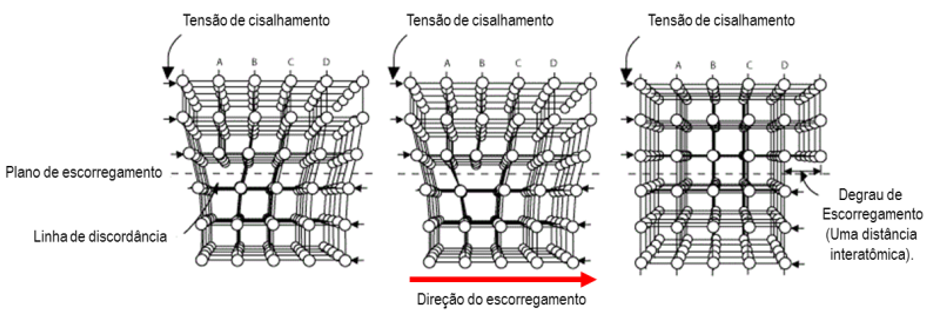
 A magnitude e a direção da distorção de rede cristalina associada a uma discordância são expressas em termos de um vetor, denominado vetor de Burgers, representado por $\stackrel{-}{b}$, como mostra a Figura 5.

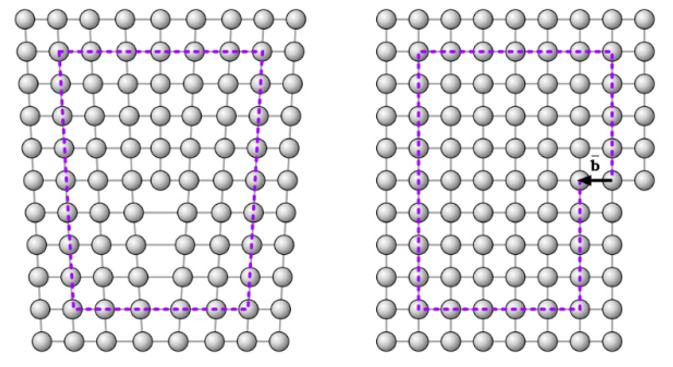
 Já a discordância do tipo espiral é um pouco mais difícil de visualizar e ela pode ser considerada como a consequência da tensão cisalhante que é aplicada para produzir a distorção. A natureza de uma discordância é definida pelas orientações relativas da linha da discordância e do vetor de Burgers. Em uma discordância em aresta, elas são perpendiculares, enquanto em uma discordância espiral, elas são paralelas.  A Figura 6 mostra a representação do movimento de uma discordância espiral.

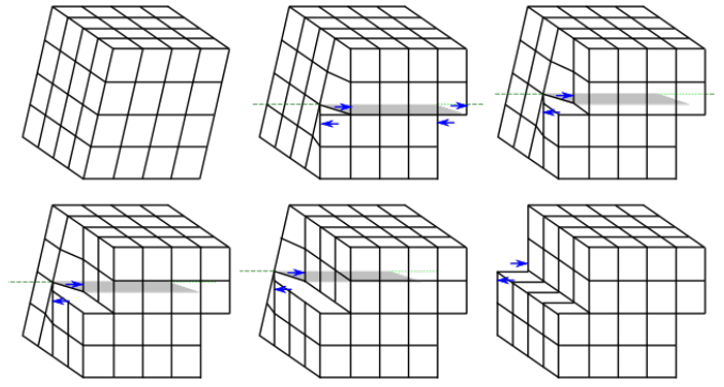
 A maioria das discordâncias nos materiais cristalinos não é nem puramente em aresta nem puramente em espiral, mas uma mistura de ambos os tipos. Por essa razão, essas discordâncias são denominadas discordâncias mistas.

As discordâncias podem ser observadas, nos materiais cristalinos, por meio de técnicas de microscopia eletrônica. Assim, todos os materiais cristalinos podem apresentar algumas discordâncias que foram introduzidas durante a solidificação ou durante uma deformação plástica, como consequência de tensões térmicas resultantes de um resfriamento rápido, por exemplo.

Outra classe de defeitos pode ser chamada de defeito interfacial. Os defeitos interfaciais são defeitos bidimensionais que aparecem em cristais que possuem estruturas cristalinas ou orientações cristalográficas diferentes. Esses defeitos podem ser divididos em: superfícies externas, contornos de grão, contornos de fase e contornos de macla.

Nos defeitos de superfície externa, os átomos de superfície não apresentam o número de coordenação adequado da estrutura cristalina do material e as ligações atômicas estão rompidas, resultando em átomos em estado de maior energia.

Com relação ao contorno de grão, ele é definido como o limite onde termina e começa outro grão. Os sólidos são geralmente constituídos por um número de grãos que podem variar em comprimento e na transição de suas orientações cristalinas em relação a um grão adjacente. Quando a diferença entre as orientações cristalinas dos grãos é pequena, utiliza-se o termo contorno de grão de baixo ângulo e quando esse desajuste de orientação é grande, utiliza-se o termo contorno de grão de alto ângulo. Observe a Figura 7, ela apresenta um esquema dos contornos de grão e a micrografa de um metal policristalino com os limites de grão evidenciados por ataque químico.

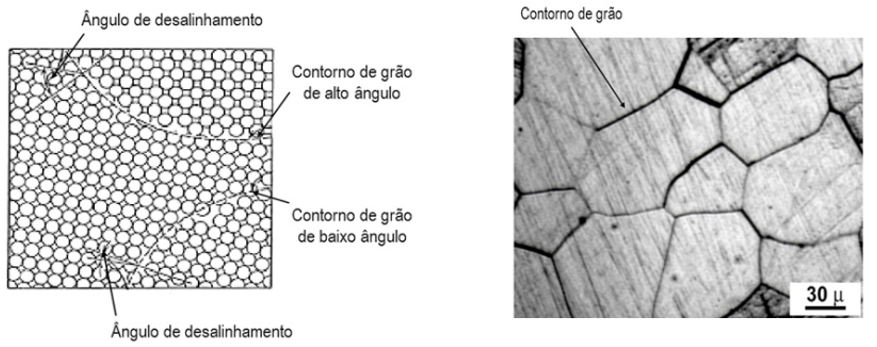
 O tamanho dos grãos pode ser controlado pela taxa de resfriamento quando um material é fundido ou tratado termicamente. Geralmente um resfriamento rápido produz grãos menores, enquanto um resfriamento lento produz grãos maiores. O tamanho do grão pode ser determinado utilizando o método desenvolvido pela Sociedade Americana para Testes e Materiais (ASTM – do inglês American Society of Testing and Materials), em que se utilizam vários quadros comparativos com números atribuídos de 1 a 10, que são chamados números do tamanho do grão. Para usar esse método uma amostra deve ser preparada adequadamente e fotografada com uma ampliação de 100 X, assim o tamanho do grão é determinado pelos grãos que mais se assemelham aos grãos da micrografa. A comparação dos quadros para determinação do tamanho de grão está relacionada ao número médio de grãos por polegada quadrada sob ampliação de 100 X. Esses parâmetros estão relacionados pela equação (4).

$N = 2^{n-1}$

Na expressão (4), N representa o úmero médio de grãos por polegada quadrada sob uma ampliação de 100X e n representa o número do tamanho do grão.  

Os contornos de fase existem nos materiais multifásicos, em que há uma fase diferente em cada lado do contorno e cada uma das fases constituintes possui suas próprias características físicas e/ou químicas distintas. Os contornos de fase possuem um papel importante na determinação das características mecânicas de algumas ligas metálicas multifásicas.

E ainda, como defeito interfacial, existe o contorno de macla, tipo especial de contorno de grão. Nesse defeito existe uma simetria em espelho específica da rede cristalina, onde os átomos em um dos lados do contorno estão localizados em posições de imagem em espelho em relação aos átomos do outro lado do contorno.

Por fim, os defeitos volumétricos, que podem ser divididos em quatro classes, com base na combinação do tamanho e do efeito da partícula. Eles podem ser: 

• Precipitados: pequenas partículas introduzidas na matriz de uma reação no estado sólido e que aumentam a resistência das ligas estruturais.
• Dispersantes: partículas maiores que se comportam como uma segunda fase e que adicionalmente influenciam o comportamento da fase primária.  
• Inclusões: são geralmente constituintes indesejáveis na microestrutura.
• Vazios (ou poros): são causadas por gases que ficaram presos durante a solidificação, ou por condensação vaga no estado sólido, e são quase sempre defeitos indesejáveis.

Análises microscópicas

Muitas vezes é necessário estudar os elementos estruturais e os defeitos que influenciam as propriedades dos materiais, visando conhecer as propriedades iniciais e como elas podem ser alteradas com a utilização controlada de defeitos.

Contudo, alguns elementos estruturais possuem dimensões macroscópicas, podendo ser observados a olho nu. No entanto, na maioria dos materiais, os grãos constituintes possuem dimensões microscópicas e seus detalhes devem ser investigados utilizando-se algum tipo de microscópio para o estudo da microscopia.  

Por essa razão, os microscópios ópticos, eletrônicos e de varredura por sonda são comumente usados para essas análises. Esses instrumentos auxiliam nas investigações de propriedades de microestruturas de qualquer material. Algumas dessas técnicas empregam equipamentos fotográficos em conjunto com o microscópio e a fotografia na qual a imagem é registrada é chamada de fotomicrografia. Adicionalmente, muitas imagens microestruturais são geradas e/ou retocadas com o auxílio de computadores.

O exame microscópico é uma ferramenta extremamente útil no estudo e na caracterização dos materiais, pois através desse dele é possível, principalmente, garantir que as associações entre as características, propriedades, estrutura e defeitos sejam compreendidos da forma correta, prevendo as propriedades dos materiais, determinando se um material foi tratado termicamente da maneira correta e verificando o tipo de uma fratura mecânica.

Dentre as técnicas utilizadas para realizar a microscopia, as mais comuns são microscopia óptica, eletrônica, de transmissão e de varredura. Vejamos cada uma separadamente.

A Microscopia Óptica, em que um microscópio óptico é empregado para estudar a microestrutura, é constituída basicamente por sistemas óptico e de iluminação. As investigações desse tipo são denominadas de metalográficas, pelo fato de que os materiais metálicos foram os primeiros materiais a serem examinados usando essa técnica. Para aplicação dessa técnica, são necessários preparos cuidadosos da superfície para revelar os detalhes importantes da microestrutura. 

A Microscopia Eletrônica é utilizada para ampliações maiores que as possíveis em um microscópio óptico, uma imagem da estrutura sob investigação é formada usando feixes de elétrons, em lugar de radiação luminosa.

Já na Microscopia Eletrônica de Transmissão, a imagem é formada por um feixe de elétrons que passa através da amostra. Os detalhes das características da microestrutura interna tornam-se acessíveis à observação; os contrastes na imagem são produzidos por diferenças no espalhamento ou difração do feixe que são produzidas entre os vários elementos da microestrutura ou defeitos.

Na Microscopia Eletrônica de Varredura, a superfície de uma amostra a ser examinada é varrida com um feixe de elétrons e o feixe de elétrons refletido (ou retroespalhado) é coletado e, então, exibido segundo a mesma taxa de varredura em um tubo de raios catódicos. A imagem na tela, que pode ser fotografada, representa as características da superfície da amostra. A superfície, polida ou não, aplicado ataque químico ou não, porém deve ser condutora de eletricidade, para isso, um revestimento metálico superficial fino deve ser aplicado sobre materiais não condutores.

Por fim, temos a Microscopia de varredura por sonda (MVS). Nesse caso, o microscópio de varredura por sonda (MVS), do qual existem diversas variedades, difere dos microscópios ópticos e eletrônicos pelo fato de que nem a luz nem elétrons são usados para formar uma imagem. Em vez disso, o microscópio gera um mapa topográfico, em uma escala atômica, que é uma representação dos detalhes e das características da superfície da amostra que está sendo examinada. Nele, são geradas imagens tridimensionais ampliadas, as quais fornecem informações topográficas sobre as características de interesse. Esses novos MVS, que permitem o exame da superfície dos materiais nos níveis atômico e molecular, forneceram uma riqueza de informações sobre uma gama de materiais, desde chips de circuitos integrados até moléculas biológicas.

Vamos Exercitar?

Relembrando o problema proposto inicialmente, como vendedor técnico da metalúrgica, você deve ser capaz de responder às dúvidas do cliente: é possível manipular a propriedade do metal? Quais impurezas ou defeitos pode haver no ferro α?

As impurezas também são consideradas defeitos pontuais e ocorrem quando átomos são inseridos na estrutura cristalina principal, formando uma solução sólida substitucional ou intersticial, dependendo do raio atômico e da alocação dos átomos nos sítios da rede, sem provocar mudança na estrutura cristalina principal.

As impurezas substitucionais são aquelas em que um átomo, diferente daqueles que formam a rede cristalina, substitui outro átomo da estrutura, com no máximo diferença de 15% do raio do átomo da estrutura original. Um exemplo de átomos de impureza substitucional são os átomos de zinco no latão, os quais possuem raio igual a 0,133 nm e substituem alguns átomos de cobre, com raio de 0,128 nm.

Já as impurezas intersticiais são definidas por átomos, muito menores do que os átomos da rede cristalina, que se encaixam no espaço vazio entre os átomos alocados na rede dessa estrutura cristalina.

A Figura 8 apresenta um esquema do que poderia acontecer com o ferro α e os átomos de carbono, formando uma solução sólida intersticial. Nesse caso, a rede cristalina é “esticada” por meio da adição de soluto intersticial, provocando uma tensão. No caso do material ferro α, na solução sólida intersticial, o carbono age como soluto e o ferro como o solvente. Dessa forma, considerando as propriedades mecânicas do material em análise, os átomos de carbono localizados nos interstícios da rede cristalina criam um campo de tensão que impede o movimento de deslocação e, consequentemente, causam um aumento da resistência mecânica. Esse processo é conhecido como cementação.

 Importante destacar que há uma quantidade de carbono que pode ser inserida no ferro $𝛼$ sem que ocorra variação em sua estrutura cristalina. E ainda, o ferro α, assim como os outros materiais sólidos, pode apresentar diversos tipos de defeitos, tais como: defeitos pontuais, defeitos lineares, defeitos interfaciais e defeitos volumétricos. E, como observamos, muitas vezes a presença desses defeitos é imprescindível para obtenção ou melhora de determinadas propriedades. Nesse caso, para aumentar a resistência superficial do material, seria necessário acrescentar carbono nos interstícios do ferro α, pelo processo de cementação.

Saiba Mais

Olá, Estudante!

Estudar sobre as imperfeições nos materiais é de fundamental importância para análise de propriedades mecânicas e compreensão das formas pelas quais elas podem ser alteradas através de sua microestrutura. Assim, para aprofundar seus conhecimentos no assunto, leia o capítulo 4 do livro Ciência dos Materiais de Shackelford. Leia o conteúdo, veja os exemplos e faça os exercícios.

SHACKELFORD, J. F. Ciência dos materiais. 6. ed. São Paulo: Pearson, 2008. E-book.

Bons estudos!

Referências Bibliográficas

ASKELAND, Donald R.; WRIGHT, Wendelin J. Ciência e engenharia dos materiais – Tradução da 4a edição norte-americana. São Paulo: Cengage Learning Brasil, 2019. E-book. ISBN 9788522128129. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128129/. Acesso em: 06 mar. 2024.

ATKINS, Peter. Físico-Química - Fundamentos, 6ª edição. Rio de Janeiro: Grupo GEN, 2017. E-book. ISBN 9788521634577. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521634577/. Acesso em: 06 mar. 2024.

JR., William D C. Ciência e Engenharia de Materiais - Uma Introdução. Rio de Janeiro: Grupo GEN, 2020. E-book. ISBN 9788521637325. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521637325/. Acesso em: 06 mar. 2024.

KOTZ, John C.; TREICHEL, Paul M.; TOWNSEND, John R.; ET.AL. Química Geral e Reações Químicas v.1. São Paulo: Cengage Learning Brasil, 2023. E-book. ISBN 9786555584516. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9786555584516/. Acesso em: 06 mar. 2024.

MAIA, D. J.; BIANCHI, J. C. de A. Química Geral e Fundamentos. São Paulo: Pearson Prentice Hall, 2007. 448 p.

NEWELL, James. Fundamentos da Moderna Engenharia e Ciência dos Materiais. Rio de Janeiro: Grupo GEN, 2010. E-book. ISBN 978-85-216-2490-5. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/978-85-216-2490-5/. Acesso em: 06 mar. 2024.

SHACKELFORD, J. F. Ciência dos materiais. 6. ed. São Paulo: Pearson, 2008. E-book. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 07 abr. 2024. 

SMITH, William F.; HASHEMI, Javad. Fundamentos de Engenharia e Ciência dos Materiais. Porto Alegre: Grupo A, 2012. E-book. ISBN 9788580551150. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788580551150/. Acesso em: 02 mar. 2024.

Difusão

Olá, Estudante! Nessa videoaula iremos compreender um pouco sobre os processos de difusão que podem ocorrer em materiais sólidos. Em nosso dia a dia é muito comum utilizarmos equipamentos em que os materiais foram produzidos por processos que envolvam algum tipo de difusão atômica para evidenciar propriedades já existentes ou modificar propriedades específicas.

Por essa razão, vamos estudar sobre esse movimento atômico que pode ocorrer em materiais, conhecido como difusão atômica, um fenômeno importante que nos auxilia na compreensão dos motivos pelos quais os materiais submetidos a tratamentos térmicos, como os metais, apresentam melhoria nas propriedades. E ainda, o estudo da difusão nos auxilia na análise e interrelação entre estrutura, processamento, propriedades e desempenho de um material. Justamente por isso é um tema de fundamental importância para sua prática acadêmica e profissional, já que as áreas de aplicação são inúmeras.

Vamos difundir o conhecimento melhorando a compreensão sobre os assuntos que serão discutidos?! Bons estudos!

Ponto de Partida

Olá, Estudante! Como está?!

Nessa aula serão abordados conceitos que envolvem a os mecanismos de difusão em sólidos. Esses conceitos são importantes para seu desenvolvimento acadêmico e profissional, pois através do processo de difusão atômica, é possível alterar propriedades dos materiais, tornando adequado para uma aplicação específica.

Dessa forma, será possível compreender, a partir dos mecanismos de difusão, como é possível colocar átomos em sólidos cristalinos, em forma de impurezas, e a devida relação com o tempo e temperatura para que isso ocorra. Depois, iremos abordar os conceitos necessários para que seja possível compreender que, para que fenômenos de difusão ocorram, é necessário a presença de defeitos na rede cristalina. Dentre os defeitos possíveis, estão as lacunas e interstícios.

Como aplicação desses conceitos, considere uma situação em que você atua como vendedor em uma indústria metalúrgica e está em negociação com um cliente para uma venda de um lote de ferro α. Durante as negociações, você percebeu que o cliente é bem exigente, e precisará explicar alguns processos e apresentar definições conceituais sobre o material e os processos de produção.

O cliente irá utilizar o ferro alfa em diversas aplicações, com diferentes condições de temperatura. Contudo, devido ao sigilo empresarial, os detalhes exatos dessa aplicação não foram revelados. E é justamente devido a essa situação que você tem sido questionado a respeito de algumas características do material, principalmente com relação às propriedades exibidas em temperaturas variadas.

Em seu último encontro com o cliente, você explicou que o ferro alfa, bem como os demais materiais, pode apresentar diversos tipos de defeitos. Dentre eles, os defeitos pontuais, lineares, interfaciais e os volumétricos. Também explicou que a presença desses defeitos é fundamental para que determinadas propriedades sejam apresentas pelo material.

Contudo, como o cliente, além de ser exigente, é curioso, fez um novo questionamento: é possível aumentar a dureza do ferro alfa? Se sim, como? Esse processo pode ocorrer para qualquer tipo de aplicação com o material?

Além disso, foi solicitado que você calculasse o fluxo difusional em uma placa de ferro com um de seus lados exposta a uma atmosfera rica em carbono e o outro lado exposta em uma atmosfera deficiente de carbono. Para isso, foi informado que a placa de ferro está a uma temperatura de 820º e, em regime estacionário, que as concentrações de carbono nas posições a 10mm e a 20mm abaixo da superfície carbonetante apresentam valor de 1,5 kg/m³ e 1kg/m³, respectivamente. Para esse cálculo, deverá ser considerado um coeficiente de difusão de $3x {10}^{-11} \frac{m^2}{s}$ na temperatura informada. 

Para responder a esses questionamentos e obter o valor solicitado, é importante compreender  e descrever os dois mecanismos de difusão atômica, apontando as principais diferenças entre eles e entender como estão relacionados com a temperatura, bem como a associação na variação de propriedades dos materiais. 

Então, vamos conhecer os conceitos necessários para resolução do problema proposto?

Bons estudos!

Vamos Começar!

Mecanismos de difusão

Por definição, a difusão pode ser determinada como um fenômeno que ocorre em materiais em qualquer estado físico (sólido, líquido e gasoso), podendo ser explicada como o fluxo de átomos ou espécies de uma região de elevada concentração a uma região de baixa concentração, dependendo do gradiente de concentração entre eles e da temperatura em que o processo ocorra.

Para os processos de difusão nos materiais sólidos, é comum definições que utilizam termos mais específicos relacionados à natureza do material. Assim, podemos dizer que o processo de difusão é o fenômeno em que ocorre o transporte de matéria através do movimento atômico, íons e macromoléculas nos metais, cerâmicas e polímeros, respectivamente. Esse movimento é dependente do gradiente de concentração e temperatura.

Atualmente, muitos são os processos tecnológicos, na melhora de propriedades do material, que necessitam do controle do processo de difusão, aumentando ou diminuindo a difusão dos elementos no material. Ou seja, os processos de difusão são utilizados para obtenção de propriedades específicas no material, como o aumento da resistência e endurecimento na superfície de aços, por exemplo.

Para melhor compreensão de como ocorre o processo de difusão, observe a Figura 1. Nela temos algumas partículas sólidas dissolvidas em água. Vemos que, inicialmente essas partículas se encontram próximas ou agrupadas (Figura 1a) e, posteriormente, elas se movem aleatoriamente na água, se distribuindo de forma aleatória e uniforme (Figura 1b). Esse movimento atômico continuará ocorrendo após a completa dissolução, mesmo sem o fluxo da água.

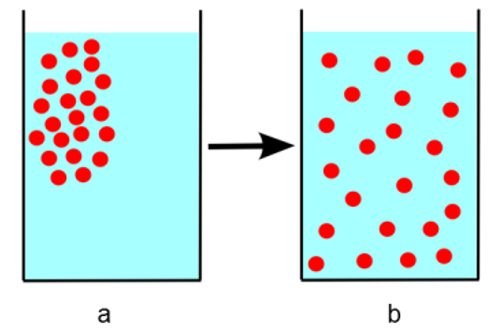
 Esse conceito é facilmente verificado quando colocamos um pouco de corante, líquido ou sólido, em um copo de água. Inicialmente o corante ficará alocado em apenas uma região do recipiente, mas com o passar do tempo, estará completamente diluído (toda água terá a cor do corante), mesmo sem mexer o copo com uma colher. Esse processo é espontâneo, mexer com a colher só vai acelerar um processo que aconteceria naturalmente.

Nos materiais sólidos, o processo de difusão ocorre de forma igual, contudo não é tão simples sua observação. Para entender esse processo em sólidos, vamos considerar um tarugo de cobre e um tarugo de estanho, incialmente em contato, como mostra a Figura 2.

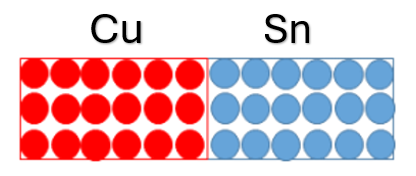
 Partindo da Figura 2, ao aquecer os tarugos a uma temperatura abaixo da temperatura de fusão, por um tempo específico, e posteriormente resfriadas, uma análise química indicaria a movimentação dos átomos de cobre e estanho conforme Figura 3. Dessa forma, seria possível ver que os átomos de cobre se difundiram entre os átomos de estanho e os átomos de estanho se difundiram entre os átomos de cobre.

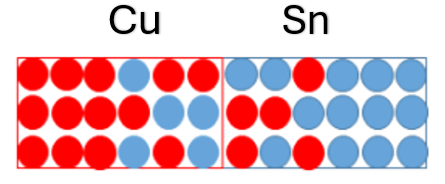
 O fenômeno em que átomos de um metal migram (difundem) para o interior de outro metal é conhecido por interdifusão, também chamado de difusão de impurezas.

A difusão não ocorre somente entre metais diferentes ou quaisquer sólidos diferentes que são colocados em contato. Esse processo também é comum em materiais puros, onde há a mudança atômica de posição na rede cristalina do próprio material, não havendo alterações de composição e nem de estrutura cristalina, chamado de autodifusão.

Para que um átomo mude sua posição em um material, é necessário que haja uma posição adjacente (vizinha) vazia e o átomo possua uma quantidade de energia capaz de romper as ligações químicas entre os seus átomos vizinhos, causando uma distorção na rede cristalina durante seu movimento.

Essa energia, de origem vibracional, é oriunda do aumento da temperatura do material, possibilitando que o átomo se movimente ao longo da rede cristalina. Importante destacar que , nos materiais metálicos, esse movimento atômico acontece prioritariamente por difusão em lacunas e difusão intersticial. Vamos entender melhor cada um desses dois tipos de difusão.

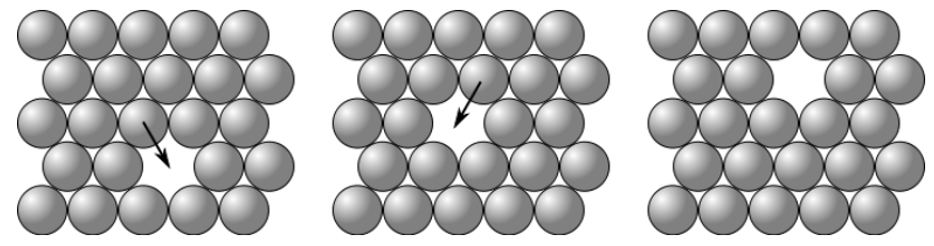
Na difusão em lacunas, tanto o átomo quanto a lacuna se movem na rede cristalina do metal, onde o átomo ocupa a posição da lacuna e a lacuna passa a ocupar a posição do átomo, como exemplo mostrado na Figura 4.

 Já em uma difusão intersticial, os átomos, inicialmente localizados em uma posição intersticial, migram para uma posição intersticial adjacente e vazia (Figura 5).

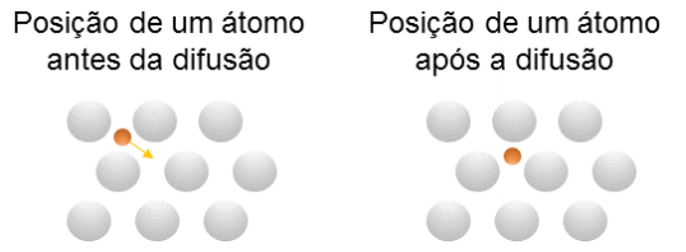
 A difusão intersticial é um fenômeno observado na interdifusão de átomos que possuem raios pequenos o bastante para ocupar os interstícios na rede cristalina principal. Dentre os elementos comuns que podem ocupar essas posições intersticiais, temos os átomos de carbono, hidrogênio, oxigênio e nitrogênio. Nesse tipo de processo, não é preciso apresentar lacunas para que ocorra a movimentação das espécies, já que elas ocupam os interstícios.

No geral, para os metais, a difusão intersticial ocorre com maior velocidade do que a difusão por lacunas, justamente pela fácil movimentação atômica devido aos tamanhos menores de raios dos átomos intersticiais. Entretanto, nos materiais cerâmicos, são os cátions que se difundem mais rapidamente do que os ânions.

Primeira e segunda Lei de Fick

De modo geral, a movimentação de átomos, ou íons, só é possível quando uma energia específica é fornecida e absorvida por eles, fazendo com que eles se movimentem, ocupando uma nova posição. Essa energia é conhecida como energia de ativação (Q). Ou seja, a energia de ativação é a energia necessária para que o átomo possa se movimentar e ocupar uma nova posição na rede cristalina de um material.

A taxa que os átomos, íons e outras partículas se difundem em um material pode ser descrita pelo fluxo de difusão (J). Esse valor indica quanto de partícula é difundida pelo tempo em um material. Dessa forma, o fluxo de difusão J corresponde ao número de átomos que se movimentam por unidade de área, em função do tempo, em regime estacionário, em uma direção (x). Matematicamente, esse fluxo é conhecido como a primeira lei de Fick, dado por (1).

$J=-D\frac{dC}{dx}=-A∆C$

Sendo D a constante de proporcionalidade, com unidades do SI de m²/s. O sinal negativo indica a direção da difusão, que ocorre contra o gradiente de concentração $\frac{dC}{dx}$ ou seja, da concentração mais alta para a mais baixa. E ainda, o gradiente de concentração $\frac{dC}{dx}$ indica como a composição do material varia com a distância.

Como exemplo, considere uma chapa de paládio, com 5mm de espessura e área de seção reta de 0,20 m². Essa chapa é utilizada como membrana difusional para o processo de purificação de hidrogênio. Nesse caso, ela é mantida entre duas atmosferas de gás: de um lado alta pressão constante e do outro, baixa pressão constante. Dessa forma, a massa de hidrogênio purificada por hora pode ser calculada. Para isso, foi informado que a concentração de hidrogênio no lado de alta pressão é de 1,5 kg.m^-3 e de 0,3 kg.m^-3 no lado de baixa pressão. E ainda, na temperatura em que o processo ocorre, o coeficiente de difusão do hidrogênio no paládio apresenta valor de $1 x {10}^{-8}\frac{m^2}{s}$.

Para encontrar a massa de hidrogênio purificada por hora, precisamos entender como o processo de difusão está ocorrendo. Assim, considerando a placa de paládio, com espessura x₀, mantida entre 2 atmosferas de gás, uma de alta pressão (na superfície em que  $x=0$, de concentração C_h) e uma de baixa pressão (na superfície em que $x=x_0$, de concentração C_l). Essa análise pode ser verificada na Figura 6.

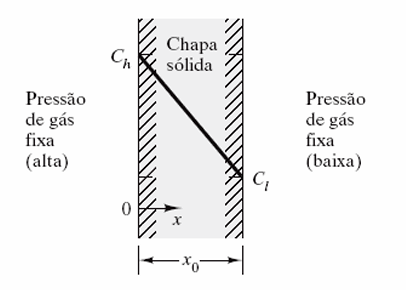
 Desse modo, aplicando a primeira Lei de Fick (1), podemos simplificar pelo gradiente de concentração em estado estacionário por (2).

$J=-D\frac{dC}{dx}=-D∆C=-D\left(-\frac{C_h-C_l}{x0}\right)$

Aplicando os valores dados em (2), temos o fluxo de difusão dado por (3).

$J=-\left(1 x {10}^{-8} \frac{m^2}{s}\right)\left[-\frac{\left(1,5kg{m}^{-3}\right)-\left(0,3kg{m}^{-3}\right)}{5x{10}^{-3}m}\right]=8,6 x {10}^{-3}kg/m^{2}h$

A massa de hidrogênio que será purificada em cada hora pode ser calculada pelo fluxo vezes a área da chapa de paládio. Esse cálculo é expresso por (4).

$m=JA=\left(8,6 x {10}^{-3} kg/m^{2}h\right)= 1,7 x {10}^{-3}kg/h$

Sendo assim, temos que a 1ª Lei de Fick é utilizada em situações em que a difusão ocorre em regime estacionário. Mas, e quando o processo ocorrer em regime transiente (não estacionário), como podemos calcular o fluxo de difusão e o gradiente de concentração? Através da 2ª Lei de Fick.

Dessa forma, para situações em que a difusão ocorre em regime não estacionário, o fluxo de difusão e o gradiente de concentração variam com o tempo. Dessa forma, é aplicada a 2ª Lei de Fick, expressa por (5).

$\frac{\partial c}{\partial t}=\frac{\partial }{\partial x}\left(D\frac{\partial C}{\partial x}\right)$

Caso o coeficiente de difusão D não seja uma função da posição x e da concentração C do átimo em difusão, a 2ª Lei de Fick pode ser simplificada por (6).

$\frac{\partial c}{\partial t}= D\left(\frac{{\partial }^{2}C}{\partial x^2}\right)$

E a solução da equação (6) depende das condições iniciais e de contorno em cada situação específica, dada por (7).

$\frac{C_x-C_0}{C_s- C_0}=1 - erf\left(\frac{x}{2\sqrt{Dt}}\right)$

Em que $C_x$ expressa a concentração em uma profundidade x após um tempo t, $C_s$ é a concentração constante na superfície e $C_0$ representa a concentração uniforme inicial dos átomos em difusão no material. Por fim, $erf \left(\frac{x}{2\sqrt{Dt}}\right)$ é definida como a função de erro de Gauss.

Siga em Frente...

Fatores que influenciam na difusão

Alguns fatores influenciam no processo de difusão. Dentre eles, a temperatura é dada como principal. Isso pelo fato de que o aumento da temperatura é devido à absorção de energia térmica necessária para que os átomos vençam a barreira energética e alterem seu estado de posição. Essa barreira energética é denominada de energia de ativação e a dependência dos coeficientes de difusão com a temperatura, ou a energia de térmica, é definida por meio da equação (8).

$D=D_0 exp\left(\frac{-Q_d}{RT}\right)$

Em que $D_0$é uma constante pré-exponencial independente da temperatura, dada em  m²/s, R é a constante universal dos gases ideais (1,987 cal/mol.K   ou 8,314 J/mol.K), T a temperatura (K) e $Q_d$ a energia de ativação para a difusão.

Geralmente, as energias de ativação são menores na difusão intersticial quando comparadas à difusão por lacunas. A Tabela 1 apresenta alguns valores das energias de ativação para a difusão de átomos em alguns materiais que são representados em pares, denominados pares de difusão, os quais apresentam a combinação do átomo de um elemento químico em difusão em uma certa matriz (metal hospedeiro). Valores baixos de energia de ativação indicam uma difusão mais fácil enquanto valores elevados indicam uma difusão mais difícil. Para o caso da autodifusão, a energia de ativação é definida como a energia necessária para se criar uma lacuna e, assim, ocorrer o movimento do átomo.

Espécie em difusão	Metal hospedeiro	D0 (m2/s)	Qd (kJ/mol)
Fe	Fe – α	2,8 x 10-4	251
Zn	Cu	2,4 x 10-5	189
Cu	Cu	7,8 x 10-5	211
Al	Al	2,3 x 10-5	144
C	Fe – α	2,8 x 10-4	251

Tabela 1. Valores das energias de ativação para a difusão de átomos. Fonte: adaptada de Callister (2020, p.136)

Como aplicação desses conceitos, vamos determinar o coeficiente de difusão do carbono a 600ºC. Para isso, aplicando (8), encontraremos o coeficiente do carbono a 600ºC por (9).

$$\begin{gathered} \left.\begin{array}{c}D=D_0 exp\left(\frac{-Q_d}{RT}\right) \\ D=\left(2,8 x {10}^{-4}\frac{m^2}{s}\right)exp\left[\frac{-251\frac{kj}{mol}}{\left(8,31\frac{J}{molK}\right)\left(600+273K\right)}\right]\\ D= 2,63 x {10}^{-19}\frac{m^2}{s}\end{array}\right\} \end{gathered}$$

Assim, os cálculos dos coeficientes de difusão indicam como a temperatura altera a magnetude da difusão.

Vamos Exercitar?

Relembrando o problema proposto inicialmente, você precisa explicar ao cliente como é possível aumentar a dureza de materiais constituídos de ferro alfa. 

Essa explicação pode ser realizada através dos conceitos de difusão atômica, definida para os materiais metálicos como o transporte de matéria por movimento atômico. Atualmente vários processos tecnológicos necessitam do controle do aumento ou da diminuição da difusão, como o endurecimento superficial de aços. Dessa forma, é possível aumentar a dureza do ferro α e a superfície de uma engrenagem de aço, graças ao processo de difusão do carbono na estrutura de ferro alfa. Ou seja, o aumento do teor de carbono é o responsável pelo aumento da dureza.

Além disso, foi solicitado que você calculasse o fluxo difusional em uma placa de ferro com um de seus lados exposta a uma atmosfera rica em carbono e o outro lado exposta em uma atmosfera deficiente de carbono. Para isso, a taxa que os átomos, íons e outras partículas se difundem em um material pode ser aferida pelo fluxo de difusão J, que corresponde ao número de átomos que se movimentam por unidade de área e por unidade de tempo em regime estacionário ao longo de uma única direção (x), expresso matematicamente pela 1ª Lei de Fick, dada por (2). Assim, substituindo em (2) as informações fornecidas, o fluxo J pode ser calculado por (9).

$\left.\begin{array}{c}J=-D\frac{dC}{dx}\\ J=-D∆C\\ J=-D\left(\frac{C_A-C_n}{x_A-x_B}\right)\\ J= -\left(3x{10}^{-11}\frac{m^2}{s}\right)\frac{\frac{\left(1,5-1\right)Kg}{m^3}}{\left({10}^{-2}-{20}^{-2}\right)m}=1,5x{10}^{-9}\frac{kg}{m^{2}s}\end{array}\right\}$

Dessa forma, foi possível explicar a possibilidade de aumento de resistência superficial através do processo de difusão e calcular o fluxo de difusão para uma situação proposta.

Saiba Mais

Olá, Estudante!

Veja os conceitos na prática pela execução dos experimentos nos simuladores propostos abaixo, na plataforma Phet:

• Difusão.

Bons estudos!

Referências Bibliográficas

ASKELAND, Donald R.; WRIGHT, Wendelin J. Ciência e engenharia dos materiais – Tradução da 4a edição norte-americana. São Paulo: Cengage Learning Brasil, 2019. E-book. ISBN 9788522128129. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128129/. Acesso em: 06 abr. 2024.

ATKINS, Peter. Físico-Química - Fundamentos, 6ª edição. Rio de Janeiro: Grupo GEN, 2017. E-book. ISBN 9788521634577. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521634577/. Acesso em: 06 abr. 2024.

JR., William D C. Ciência e Engenharia de Materiais - Uma Introdução. Rio de Janeiro: Grupo GEN, 2020. E-book. ISBN 9788521637325. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521637325/. Acesso em: 06 abr. 2024.

NEWELL, James. Fundamentos da Moderna Engenharia e Ciência dos Materiais. Rio de Janeiro: Grupo GEN, 2010. E-book. ISBN 978-85-216-2490-5. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/978-85-216-2490-5/. Acesso em: 06 abr. 2024.

SHACKELFORD, J. F. Ciência dos materiais. 6. ed. São Paulo: Pearson, 2008. E-book. Disponível em: https://plataforma.bvirtual.com.br. Acesso em: 07 abr. 2024. 

SMITH, William F.; HASHEMI, Javad. Fundamentos de Engenharia e Ciência dos Materiais. Porto Alegre: Grupo A, 2012. E-book. ISBN 9788580551150. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788580551150/. Acesso em: 06 abr. 2024.

Videoaula de Encerramento

Olá, estudante! Nessa videoaula você irá conhecer os principais conceitos que envolvem as estruturas cristalinas. Compreenderá quando um material pode ser classificado como cristalino, como identificar a célula unitária e conhecerá os 14 tipos possíveis de estruturas cristalinas existente para os materiais. Com base na estrutura cristalina, os pontos, direções e planos cristalográficos podem ser obtidos. E mais, analisaremos os tipos de defeitos que os materiais podem apresentar e como isso influencia em suas propriedades. Para finalizar, abordaremos os conceitos de difusão em sólidos e como esse processo pode variar com a temperatura. Sendo possível aplicação desses conceitos na resolução de problemas de engenharia.

Os conteúdos citados são importantes para sua prática profissional, já que são muitos os produtos fabricados com materiais cristalinos, seja um componente ou sua totalidade.

Vamos produzir um entendimento de longo alcance, evidenciando os conceitos, difundindo conhecimento!! Bons estudos!

Ponto de Chegada

Olá, estudante! Para desenvolver a competência dessa unidade, que consiste em compreender os diferentes arranjos atômicos e as imperfeições presentes em sólidos, assim como entender os mecanismos de difusão atômica, você deve primeiramente saber que os materiais podem apresentar ou não ordenamento atômico. Ou seja, na formação dos materiais, independentemente do estado físico da matéria, os átomos e/ou íons podem se organizar em três tipos de arranjos diferentes: sem ordem (preenchimento aleatório de todo o espaço em que o material está confinado), ordem de curto alcance (arranjo espacial dos átomos se estende apenas aos vizinhos mais próximos de cada átomo) e ordem de longo alcance (arranjo atômico espacial se estende por todo material e os átomos formam um padrão regular, repetitivo, como grades ou redes).

Os materiais amorfos são caracterizados assim por apresentarem ordenamento de curto alcance, e se formam quando o processo de fabricação não permite a organização dos átomos em arranjos periódicos. Já os materiais cristalinos são aqueles em que os átomos estão posicionados segundo um arranjo periódico repetitivo ao longo de grandes distâncias atômicas, podendo contemplar todo material. Importante destacar que algumas características dos materiais dependem do tipo de estrutura cristalina que apresentam.

São muitas as formas possíveis para a estrutura cristalina nos materiais, estando presente em todas elas o ordenamento atômico de longo alcance. Essas estruturas variam com formas mais simples (apresentadas pelos metais) até as excessivamente complexas, como aquelas exibidas por alguns materiais cerâmicos e poliméricos.

O ordenamento de longo alcance em materiais sólidos cristalinos indica que pequenos grupos de átomos formam um padrão que se repete ao longo do material. Assim, quando descrevemos uma estrutura cristalina, é interessante subdividir a estrutura total em pequenas entidades que se repetem, chamadas células unitárias, ou seja, a menor unidade de repetição na formação de um cristal. Ou seja, ela é a unidade estrutural básica da estrutura cristalina e define a estrutura por meio da sua geometria e das posições dos átomos no seu interior.

Para os materiais metálicos, existem 4 tipos possibilidades de estruturas cristalinas: cúbica simples (CS), cúbica de corpo centrado (CCC), cúbica de face centrada (CFC) e hexagonal compacta (HC).

A estrutura cristalina cúbica simples (CS) possui número de coordenação igual a 6 e, no interior de cada célula unitária, há 1 átomo completo. Seu parâmetro de rede é dado por $a=2R$ e seu volume $8R^3$. Por fim, apresenta FEA de 0,52. Apenas um único elemento cristaliza em uma célula unitária cúbica simples: o polônio (Po), elemento radioativo e extremamente tóxico. A razão pela qual os metais não se cristalizam nessa estrutura é devido ao ineficiente empacotamento atômico, já que somente 52% do seu volume total é preenchido.

A estrutura cúbica de face centrada (CFC) possui número de coordenação igual a 12 e, no interior de cada célula unitária, há 4 átomos completos. Seu parâmetro de rede é dado por $a=2R\sqrt{2}$ e seu FEA é de 0,74, ou seja, apresenta 74% de seu volume total é preenchido.

A estrutura cúbica de corpo centrada (CCC) possui número de coordenação igual a 8 e, no interior de cada célula unitária, há 2 átomos completos. Seu parâmetro de rede é dado por $a=\frac{4R}{\sqrt{3}}$e seu FEA é de 0,68. Essa é uma estrutura bastante encontrada nos metais, assim com a estrutura CFC.  

Por fim, a estrutura hexagonal compacta (HC). O número de átomos por célula em uma estrutura cristalina do tipo HC é calculado considerando um sexto de cada átomo em um vértice na face superior e inferior (para um total de 12 átomos em vértices), 2 átomos nos centros de faces (um em cada uma das faces superior e inferior) e 3 átomos interiores no plano intermediário, totalizando 6 átomos por célula HC. E ainda, nas estruturas HC temos os parâmetros “a” e “c” que representam a menor e a maior dimensão da célula unitária, respectivamente. A razão entre eles apresenta valor de 1,633, ou seja $\frac{c}{a}=1,633$. Contudo, alguns metais HC apresentam um desvio em relação a esse valor ideal da razão dos parâmetros. Nessa estrutura cristalina, assim como na CFC, o número de coordenação possui valor de 12 e o fator de empacotamento atômico, 0,74.  

O conhecimento do tipo de célula unitária e da estrutura cristalina de um sólido possibilita o cálculo da sua massa específica teórica $𝜌$ (1).

$\rho =\frac{nA}{V_c{N}_A}$ 

Para o cálculo da massa específica teórica, n é o número de átomos em cada célula, A o número da massa atômica, V_c é o volume da célula unitária e N_A a constante de Avogadro, $6,023 x {10}^{23} átomos/mol$.

De modo geral, as estruturas para os cristais podem ser classificadas de acordo com a simetria das células unitárias, existindo um total de sete tipos fundamentalmente distintos dessas células que diferem nos comprimentos relativos das arestas (a, b e c) e dos ângulos formados entre elas (α, β e γ). Por essa razão, com base nesses dados, existem sete possíveis combinações entre os valores de a, b e c e $𝛼$, $𝛽$ e $𝛾$, em que cada combinação é representada por um sistema cristalino distinto, totalizando 14 tipos de estruturas cristalinas, chamadas rede de Bravais. A rede de Bravais é composta pelas seguintes redes cristalinas: três tipos cúbicos, um tipo romboédrico, quatro tipos ortorrômbicos, dois tipos tetragonais, um tipo hexagonal, um tipo triclínico e dois tipos monoclínicos.

Para analisar uma estrutura cristalina, normalmente se faz necessário especificar um ponto, uma direção ou um plano no estudo da cristalografia dos átomos.  

A localização de átomos ou a posição de qualquer ponto dentro da célula unitária pode ser obtida através de coordenadas cartesianas na forma de múltiplos fracionários dos comprimentos das arestas que a célula unitária possui. Para isso, basta alocar o pronto principal da célula sob a origem de um sistema cartesiano e verificar a distância dos pontos em relação à origem, levando em consideração o tamanho de aresta da célula cristalina igual a um.  

Já uma direção cristalográfica é definida como uma linha direcionada entre dois pontos, ou duas coordenadas, também denominada de vetor. Para obter os três índices direcionais, devemos:

• Determinar as coordenadas de dois pontos alocados na direção em estudo.
• Subtrair as coordenadas do ponto final das coordenadas do ponto inicial, a fim de obter o número de parâmetros de rede percorridos na direção de cada eixo do sistema de coordenadas.
• Eliminar as frações por meio de divisão/multiplicação dos resultados da subtração para obter os menores números inteiros possíveis.
• Apresentar os índices entre colchetes [$uvw$]. Caso haja algum sinal negativo, represente-o com uma barra sobre o número.

Assim como as direções, os planos cristalográficos podem ser representados através de índices de Miller. Para isso, é considerado uma célula unitária como base em um sistema de coordenadas (x, y e z). Para determinar os índices $hkl$, será necessário:

• Identificar os pontos em que os planos interceptam os eixos x, y e z considerando o número de parâmetros de rede.
• Calcular os inversos das intersecções.
• Eliminar as frações.
• Colocar os números resultantes entre parênteses ( ) e utilizar a barra sobre o índice caso apresente valor negativo.

As estruturas cristalinas apresentadas pelos materiais podem ser idealizadas e simplificadas, de maneira que possam ser utilizadas para compreensão de muitos princípios importantes que regem o comportamento dos sólidos. Contudo, cristais reais apresentam grande número de defeitos (imperfeições), na rede cristalina, que variam desde a quantidade de impurezas até a falta de átomos ou íons. Esses defeitos, ou imperfeições, são importantes para a estabilidade do material e impactam diretamente nas propriedades que possuem.

Dentre os tipos de defeitos possíveis em sólidos cristalinos, os mais comuns são conhecidos como: defeitos pontuais, defeitos lineares, defeitos interfaciais e defeitos volumétricos.

Os defeitos pontuais são denominados por regiões em que há ausência de um átomo ou o átomo se encontra em uma região irregular na estrutura cristalina. Entre os defeitos pontuais, temos lacunas, autointersticial, impurezas substitucionais e intersticiais. A lacuna é o defeito mais simples e, como o próprio nome sugere, é dado pela ausência de um átomo na rede cristalina.

A adição de átomos em um metal resulta na formação de uma solução sólida, que se forma quando, à medida que os átomos de soluto (em menor quantidade) são adicionados ao material hospedeiro (solvente, em maior quantidade), a estrutura cristalina é mantida e nenhuma estrutura nova é formada, mas esse processo resulta em alteração de propriedades no material. As soluções sólidas podem ser do tipo substitucional (há substituição de um átomo da rede cristalina por outro átomo, de outro elemento químico) ou intersticial (átomos menores se alocam nos interstícios da rede cristalina).

Além dos defeitos pontuais, uma estrutura pode apresentar  discordâncias, que são defeitos lineares observados em átomos que estão desalinhados. Ou seja, as discordâncias são defeitos em que alguns átomos se encontram fora da sua posição inicial na estrutura cristalina, em que sua principal função consiste em controlar a resistência ao escoamento e a subsequente deformação plástica dos sólidos cristalinos a temperaturas normais, sem que ocorra transformação de fase. Elas podem ser do tipo aresta e a discordância espiral.

E ainda, há situações em que o fluxo de átomos ou espécies de uma região de elevada concentração migra para uma região de baixa concentração, dependendo do gradiente de concentração entre eles e da temperatura em que o processo ocorra. Esse fenômeno é conhecido como difusão, e pode ocorrer me qualquer estado físico da matéria. Assim, podemos dizer que o processo de difusão é o fenômeno em que ocorre o transporte de matéria através do movimento atômico, dependendo do gradiente de concentração e temperatura.

Normalmente, esse processo é utilizado para modificar e melhorar algumas propriedades apresentadas pelos materiais sólidos, como o aumento da resistência e endurecimento na superfície de aços, por exemplo.

A difusão pode ocorrer de algumas formas. Dentre elas, o fenômeno em que átomos de um metal migram (difundem) para o interior de outro metal é conhecido por interdifusão, também chamado de difusão de impurezas.

A difusão não ocorre somente entre metais diferentes ou quaisquer sólidos diferentes que são colocados em contato. Esse processo também é comum em materiais puros, onde há a mudança atômica de posição na rede cristalina do próprio material, não havendo alterações de composição e nem de estrutura cristalina, chamado de autodifusão.

Em qualquer forma de difusão, para que um átomo mude sua posição em um material, é necessário que haja uma posição adjacente vazia e o átomo possua uma quantidade de energia capaz de romper as ligações químicas entre os seus átomos vizinhos, causando uma distorção na rede cristalina durante seu movimento.  

Importante destacar que , nos materiais metálicos, esse movimento atômico acontece prioritariamente por difusão em lacunas (tanto o átomo quanto a lacuna se movem na rede cristalina do metal, onde o átomo ocupa a posição da lacuna e a lacuna passa a ocupar a posição do átomo) e difusão intersticial (os átomos, inicialmente localizados em uma posição intersticial, migram para uma posição intersticial adjacente e vazia).

Essa movimentação de átomos, ou íons, só é possível quando uma energia específica é fornecida e absorvida por eles, fazendo com que eles se movimentem, ocupando uma nova posição. Essa energia é conhecida como energia de ativação (Q). Ou seja, a energia de ativação é a energia necessária para que o átomo possa se movimentar e ocupar uma nova posição na rede cristalina de um material.

A taxa que os átomos, íons e outras partículas se difundem em um material pode ser descrita pelo fluxo de difusão (J). Esse valor indica quanto de partícula é difundida pelo tempo em um material. Dessa forma, o fluxo de difusão J corresponde ao número de átomos que se movimentam por unidade de área, em função do tempo, em regime estacionário, em uma direção (x). Matematicamente, esse fluxo é conhecido como a primeira lei de Fick, dado por (2).

$J=-D\frac{dC}{dx}=-D∆C$

Sendo D a constante de proporcionalidade, com unidades do SI de m²/s. O sinal negativo indica a direção da difusão, que ocorre contra o gradiente de concentração $\frac{dC}{dx}$ou seja, da concentração mais alta para a mais baixa. E ainda, o gradiente de concentração $\frac{dC}{dx}$indica como a composição do material varia com a distância. 

Contudo, quando o processo ocorre em regime transiente (não estacionário) a 2ª Lei de Fick é utilizada para o cálculo do fluxo (J). Matematicamente, é dada por (3).

$\frac{\partial c}{\partial t}=\frac{\partial }{\partial x}\left(D\frac{\partial C}{\partial x}\right)$

Caso o coeficiente de difusão D não seja uma função da posição x e da concentração C do átimo em difusão, a 2ª Lei de Fick pode ser simplificada por (4).

$\frac{\partial c}{\partial t}=D\left(\frac{{\partial }^{2}C}{\partial x^2}\right)$

E a solução da equação (3) depende das condições iniciais e de contorno em cada situação específica, dada por (5).

$\frac{C_x-C_0}{C_s-C_0}=1-erf\left(\frac{x}{2\sqrt{Dt}}\right)$

Por fim, alguns fatores influenciam no processo de difusão. Dentre eles, a temperatura é dada como principal. Isso pelo fato de que o aumento da temperatura é devido à absorção de energia térmica necessária para que os átomos vençam a barreira energética e alterem seu estado de posição. Essa barreira energética é denominada de energia de ativação e a dependência dos coeficientes de difusão com a temperatura, ou a energia de térmica, é definida por meio da equação (6).

$D=D_{0}exp\left(\frac{-Q_d}{RT}\right)$

Em que $D_0$ é uma constante pré-exponencial independente da temperatura, dada em  m²/s, R é a constante universal dos gases ideais (1,987 cal/mol.K   ou 8,314 J/mol.K), T a temperatura (K) e $Q_d$ a energia de ativação para a difusão.

É Hora de Praticar!

Olá, Estudante! Nesse estudo de caso, considere uma situação em que você é estagiário em uma grande empresa de desenvolvimento de tecnologia. Essa empresa é conhecida por desenvolver pesquisas e fabricação de novos materiais, visando aplicações específicas em projetos de engenharia.

Nesse momento, a equipe de desenvolvimento está realizando um estudo para a fabricação de um material metálico que apresente alta resistência superficial para suportar impactos durante a sua utilização. E ainda, é interessante que esse material apresente propriedades magnéticas (material ferromagnético).  

O foco principal da equipe de desenvolvimento consiste em fabricar um material com um valor específico de resistência superficial. O tipo de material já foi escolhido, eles estão apenas finalizando os estudos para chegarem ao valor da propriedade desejada.

Nesse momento, você foi chamado à sala de projetos para que pudesse desenvolver uma pesquisa e compreender melhor os conceitos que estão envolvidos na fabricação desse material, para aprofundar seu conhecimento na área. Você foi informado do que estavam desenvolvendo e pediram que você, com base em suas pesquisas, confirmasse a eles qual o material estava sendo utilizado e por qual processo a modificação dessa propriedade seria possível. E mais, um relatório com todas as informações a respeito da estrutura cristalina desse material deverá ser entregue ao seu supervisor direto.

Bons estudos!

Reflita

• Existem materiais que são, ao mesmo tempo, amorfos e cristalinos?
• A mudança nas estruturas e redes cristalinas sempre envolvem uma transformação nas propriedades dos materiais?
• Pode existir um material sem nenhum tipo de defeito? Por quê?
• Em processos a temperatura constante pode haver difusão? O estado da matéria influência?

Resolução do estudo de caso

Retomando ao estudo de caso, você deverá realizar uma pesquisa para identificar qual material a equipe de desenvolvimento está utilizando no projeto atual. Para isso, foi informado que é um material metálico que apresenta alta resistência superficial para suportar impactos durante a sua utilização. E ainda, é interessante que esse material apresente propriedades magnéticas (material ferromagnético). Foi pedido também para que você descrevesse todas as informações a respeito da estrutura cristalina desse material.

Com o desenvolvimento de suas pesquisas, você identificou que o material que está sendo usado é o ferro alfa (α–Fe), material metálico de estrutura cristalina cúbica de corpo centrado (CCC). Um exemplo dessa estrutura cristalina é apresentado na Figura 1. 

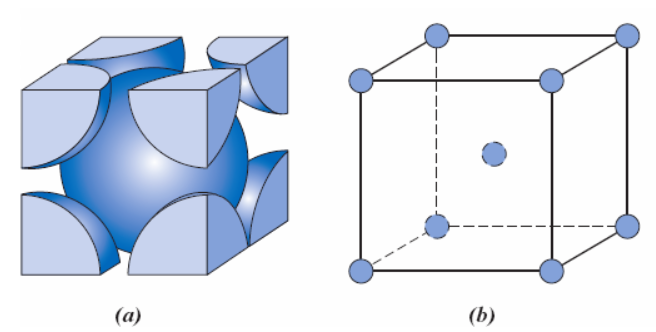
 A estrutura CCC apresenta número de coordenação igual a 8. Olhando para os átomos, eles estão localizados nos oito vértices da célula, contribuindo com 1/8 de sua massa total; além disso, há um único átomo inteiro no centro do cubo. Dessa forma, o número de átomos por célula em uma estrutura CCC pode ser calculado por (7).

$nº átomos célula \left(CCC\right)=\left(\frac{1}{8}átomo vértice\right)\left(8 vértices\right)+\left(1 átomo centro\right)= 2 átomos por célula$

Ou seja, são 2 átomos inteiros em cada célula unitária do tipo CCC.  

Para o cálculo do parâmetro de rede

a$a$

da célula cristalina CCC, é preciso verificar a diagonal do cubo, local em que átomos se tocam uns nos outros (Figura 2). Como há dois raios atômicos a partir do átomo central e um raio atômico de cada um dos átomos do vértice, podemos aplicar a equação de Pitágoras e chegamos ao parâmetro de rede, considerando o raio atômico como r, de $a = \frac{4r}{\sqrt{3}}$.

 

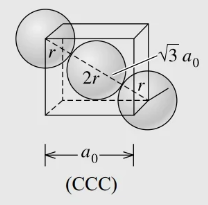
E ainda, com o valor do parâmetro de rede, calcular o FEA, que nesse caso terá um valor de 68%, ou seja, apresenta 68% de seu volume total é preenchido. Como exemplo, o cromo, o ferro e o tungstênio exibem uma estrutura CCC.

Para o ferro com estrutura cristalina no tipo CCC, sua densidade teórica também pode ser calculada, considerando que possui um parâmetro de rede de 0,2866 nm e peso atômico de 55,847 g/mol. Esse cálculo é expresso por (8).

$\left.\begin{array}{c}\rho =\frac{nA}{V_c{N}_A}\\ \rho =\frac{\left(2 átomos/cela\right)\left(55,847 g/mol\right)}{{\left(2,866 x {10}^{-8}cm\right)}^3\left(6,023 x {10}^{23}átomos/mol\right)}=7,879\frac{g}{c{m}^3}\\ \end{array}\right\}$

E, por fim, o processo de aumento de resistência superficial pode ser realizado através da cementação, que é um fenômeno de difusão intersticial, em que, nesse caso, átomos de carbono são difundidos na superfície do aço, considerando um gradiente de concentração e variação de temperatura.

Com esses dados, você finaliza sua pesquisa e pode escrever o relatório com todas as informações obtidas.

Dê o play!

Assimile

Olá, estudante! No mapa mental abaixo você verá os principais assuntos relacionados à estrutura cristalina. Importante conhecer cada definição para poder realizar as aplicações necessárias em estudos relacionados às estruturas cristalinas e propriedades dos materiais.

 

Referências

ASKELAND, Donald R.; WRIGHT, Wendelin J. Ciência e engenharia dos materiais – Tradução da 4a edição norte-americana. São Paulo: Cengage Learning Brasil, 2019. E-book. ISBN 9788522128129. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788522128129/. Acesso em: 10 abr. 2024.

JR., William D C. Ciência e Engenharia de Materiais - Uma Introdução. Rio de Janeiro: Grupo GEN, 2020. E-book. ISBN 9788521637325. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788521637325/. Acesso em: 10 abr. 2024.

NEWELL, James. Fundamentos da Moderna Engenharia e Ciência dos Materiais. Rio de Janeiro: Grupo GEN, 2010. E-book. ISBN 978-85-216-2490-5. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/978-85-216-2490-5/. Acesso em: 10 abr. 2024.

SMITH, William F.; HASHEMI, Javad. Fundamentos de Engenharia e Ciência dos Materiais. Porto Alegre: Grupo A, 2012. E-book. ISBN 9788580551150. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788580551150/. Acesso em: 10 abr. 2024.