Cinemática: Estudo Do Movimento Dos Corpos

Grandezas escalares e vetoriais na cinemática

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la?
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante! As grandezas físicas moldam nossa compreensão do universo, estando presentes em praticamente todas as situações que vivenciamos. Seja na cozinha ao preparar uma receita, observando o movimento dos planetas ou mesmo entendendo a força do vento em um dia chuvoso, as grandezas estão lá, nos ajudando a quantificar e compreender o mundo ao nosso redor.

Você já parou para pensar por que usamos determinadas unidades quando falamos de distância, tempo ou volume? Já se questionou sobre a diferença entre quantidades que nos dão apenas um valor e aquelas que também nos indicam uma direção? E a misteriosa notação científica, por que é tão útil em tantas áreas? Estas e outras questões serão abordadas ao longo desta aula.

Para começar nossa jornada, imagine que você está tentando descrever a direção e força do vento em um dia tempestuoso. Por que seria importante saber tanto a magnitude quanto a direção desse vento? Como as grandezas vetoriais podem nos ajudar a entender essa e outras situações semelhantes?

Esteja pronto para uma aventura pelo universo das grandezas físicas. Com um pouco de curiosidade e dedicação, ao final desta aula, você terá uma nova perspectiva sobre muitos fenômenos ao seu redor. Então, está preparado para essa exploração? Vamos lá!

Vamos Começar!

As grandezas físicas

Uma grandeza física é basicamente algo que conseguimos medir. Imagine distância, tempo, temperatura e pressão: todos são exemplos de grandezas físicas. Agora, pense na beleza de uma paisagem, na emoção de ouvir uma música ou no sabor de sua comida favorita. Difícil medir numericamente, certo? É porque são qualidades, não grandezas físicas.

Para entender melhor, dividimos as grandezas físicas em dois grupos: escalares e vetoriais.

• Escalares: são aquelas grandezas que precisamos apenas de um número para descrever. Por exemplo, se dissermos que um cachorro pesa 15 quilogramas, já temos a informação completa. Em resumo, a temperatura é um escalar, assim como a massa e o tempo.
• Vetoriais: aqui, um número sozinho não basta. Precisamos saber mais detalhes. Por exemplo, ao falar de uma velocidade, não basta dizer que o carro está a "40 km/h". Precisamos saber para onde ele vai (a direção) e para que lado (o sentido). Então, grandezas que têm valor, direção e sentido são vetoriais. Se você imaginar uma maçã caindo na sua cabeça, o impacto que você sente é uma força (uma grandeza vetorial). Outros exemplos são pressão e força.

Notação científica

Quando medimos algumas coisas, os números podem ser extremamente grandes ou extremamente pequenos. Vejamos alguns exemplos:

• A distância da Terra ao Sol é de cerca de 149.600.000 km.
• O tempo que um pulso de luz leva para viajar 1 centímetro é aproximadamente 0,00000003 segundos.
• A distância da Terra à Lua é de 384.000 km.
• E o comprimento de uma molécula de DNA? Está por volta de 0,000000002 m.

Com números tão grandes ou tão pequenos assim, usar a notação científica, que se baseia nas potências de 10, facilita muito a nossa vida.

A notação científica é uma maneira concisa e padronizada de escrever números muito grandes ou muito pequenos. Em ciências e matemática, frequentemente nos deparamos com números que têm muitos dígitos ou são extremamente próximos de zero. Escrever esses números em sua forma completa pode ser demorado e sujeito a erros. Portanto, a notação científica serve para simplificar essas expressões.

A estrutura básica da notação científica é $\mathit{a}\mathbf{.}{\mathbf{10}}^{\mathbf{n}}$, sendo que “a” é um número entre 1 (inclusive) e 10 (exclusive) e “n” é um número inteiro que representa a potência de 10. Assim, o valor absoluto (ou módulo) de um número “b” é como se estivéssemos combinando dois números: um chamado “a”, que fica entre 1 e 10; e outro que é uma potência de 10, ou seja, 10ⁿ. Então, podemos representar isso como $\mathit{b}\mathbf{=}\mathit{a}\mathbf{.}{\mathbf{10}}^{\mathbf{n}}$.

Veja alguns exemplos:

• O número 300.000.000 (trezentos milhões) pode ser escrito como (3.10⁸) em notação científica.
• O número 0,000045 (quarenta e cinco milionésimos) pode ser representado como (4,5.10^-5).
• A distância média da Terra ao Sol é aproximadamente 149.600.000 km, o que pode ser escrito como (1,496.10⁸) km.

Dica rápida para notação científica:

1. Para números maiores que 1: mova a vírgula para a esquerda, parando no primeiro número que aparecer. O total de vezes que você moveu a vírgula será o expoente positivo de 10ⁿ.
2. Para números menores que 1: mova a vírgula para a direita até encontrar o primeiro número que não seja zero. O total de vezes que você moveu a vírgula será o expoente negativo de 10ⁿ.

Lembrando que, ao utilizar a notação científica, estamos buscando simplicidade e precisão. É uma ferramenta valiosa para cientistas, matemáticos e qualquer pessoa que lide com números extremamente grandes ou pequenos.

Sistema Internacional de Unidades (SI)

O Sistema Internacional de Unidades, conhecido pela sigla SI, é o sistema de medidas adotado mundialmente para padronizar e simplificar a comunicação científica e técnica. Estabelecido pela Conferência Geral de Pesos e Medidas em 1960, o SI tem como base sete unidades fundamentais a partir das quais todas as outras unidades são derivadas. A adoção de um sistema padrão facilita o entendimento mútuo, a colaboração e a comparação de resultados entre diferentes pesquisas e indústrias ao redor do mundo. A Tabela 1 indica as sete unidades fundamentais adotadas pelo sistema métrico, ou seja, SI.

Grandeza	Unidade	Símbolo
Comprimento	metro	m
Massa	quilograma	kg
Tempo	segundo	s
Corrente elétrica	ampère	A
Temperatura termodinâmica	kelvin	K
Quantidade de matéria	mol	mol
Intensidade luminosa	candela	cd

Tabela 1 | Grandezas de base e unidades de base do SI. Fonte: adaptada de Inmetro (2007).

No SI, temos as "unidades derivadas", que são como combinações das unidades básicas. É como criar um prato novo com ingredientes básicos! As "unidades derivadas coerentes" só usam as unidades de base e não têm números extras. Por exemplo, a velocidade (m/s) é uma unidade derivada coerente, porque só usa unidades de base. Juntando todas as unidades de base e as unidades derivadas coerentes, temos um conjunto organizado chamado "conjunto de unidades coerentes do SI". A Tabela 2 mostra algumas das unidades coerentes do SI.

Grandeza	Nome	Símbolo	Com outras unidades do SI	Unidades base do SI
Frequência	Herts	Hz		$s^{-1}$
Força	Newton	N		$m·\frac{kg}{s^2}$
Pressão/Tensão	Pascal	Pa	$\frac{N}{m^2}$	$\frac{kg}{m·s^2}$
Energia	Joule	J	$\frac{N}{m}$	$\frac{m^2·kg}{s^2}$
Potência	Watt	W	$\frac{J}{s}$	$\frac{m^2·kg}{s^3}$

Tabela 2 | Principais unidades coerentes do SI. Fonte: elaborada pelo autor.

O Sistema Internacional (SI) tem prefixos especiais para representar valores muito grandes ou muito pequenos. Isso facilita a nossa vida! Exemplo: "1 quilômetro" é mais simples que "1.000 metros". O "quilo-" é um prefixo que significa "mil". A Tabela 3 indica os símbolos e os prefixos de acordo com o SI.

Prefixo	Símbolo	Potência de base 10	Equivalente decimal
tera	T	1012	1.000.000.000.000,00
giga	G	109	1.000.000.000,00
mega	M	106	1000000
quilo	k	103	1000
hecto	h	102	100
deca	da	101	10
nenhum	nenhum	100	1
deci	d	10-1	0,10
centi	c	10-2	0,01
mili	m	10-3	0,001
micro	u	10-6	0,000001
nano	n	10-9	0,000000001
pico	p	10-12	0,000000000001

Tabela 3 | Nomenclatura e símbolos das principais potências de 10. Fonte: adaptada de Inmetro (2007).

E tem mais! Podemos combinar esses prefixos com qualquer unidade de base ou derivada. Isso nos dá muitas opções para representar diferentes grandezas.

Em algum momento da vida acadêmica ou profissional, às vezes, precisamos trocar de uma unidade para outra. Como fazemos isso? Com a regra de três simples! Mas precisamos conhecer algumas relações entre as unidades. Vamos conhecê-las observando o Tabela 4.

Conversões de comprimento

1 km (um quilômetro) = 1000 m (mil metros)

1 m (um metro) = 100 cm (cem centímetros)

1 m (um metro) = 1000 mm (mil milímetros)

Conversões de massa

1 kg (um quilograma) = 1000 g (mil gramas)

1 g (um grama) = 1000 mg (mil miligramas)

Conversões de tempo

1 h (uma hora) = 60 min (sessenta minutos)

1 min (um minuto) = 60 s (sessenta segundos)

1 h (uma hora) = 3600 s (três mil e seiscentos segundos)

1 dia = 24 h (vinte e quatro horas

Tabela 4 | Principais correspondências entre as unidades. Fonte: elaborado pelo autor.

Não se preocupe em decorar todos os fatores de conversão. Foque nos mais usados em mecânica. Lembre-se: a internet e os apps estão aí para ajudar nas conversões mais específicas!

Agora que conhecemos as grandezas físicas, vamos direcionar nossa atenção para as grandezas vetoriais, destacando suas particularidades e relevância no estudo da física.

Siga em Frente...

As grandezas vetoriais

Grandezas como tempo, massa e temperatura são diretas: precisam só de um número e uma unidade. Essas grandezas são classificadas como "grandezas escalares".

Mas algumas grandezas precisam de mais informações. Além do número, temos que saber a direção e o sentido. São as "grandezas vetoriais", como velocidade $\left(\overrightarrow{v}\right)$, aceleração $\left(\overrightarrow{a}\right)$ e força $\left(\overrightarrow{F}\right)$. E a dica é que elas geralmente têm uma flechinha em cima na representação.

Agora, vamos entender o que é um vetor? Um vetor é uma quantidade física que tem tanto magnitude (módulo) quanto direção. A magnitude fornece informações sobre o "quanto" de algo, enquanto a direção fornece informações sobre o "onde" ou "em que direção". Em termos simples, um vetor é frequentemente representado por uma seta, onde o comprimento da seta indica a magnitude e a orientação da seta indica a direção. Ou seja, um vetor é como uma setinha que aponta de um lugar para outro e, para você compreender, vamos verificar como é composto um vetor.

Origem e extremidade:

• Origem é de onde começa.
• Extremidade é para onde aponta.
• Ao desenhar um vetor em um plano ou espaço, ele geralmente é representado por uma seta. A origem (ou "cauda") da seta é o ponto de partida do vetor, enquanto a ponta (ou "cabeça") da seta indica a direção e o ponto final.

Módulo:

• É o tamanho da setinha. Portanto, a magnitude ou o módulo do vetor é proporcional ao comprimento da seta.

Direção e sentido:

• Direção é a linha da setinha.
• Sentido é para onde a ponta aponta.
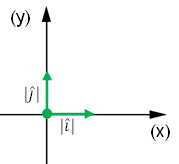
• E os gráficos "x" e "y", conhecidos como plano cartesiano? Na direção horizontal (eixo x): sentido positivo para a direita (leste) e representado pelo versor $\hat{i}$, sendo que $\left|\hat{i}\right|=1$. Na direção vertical (eixo y): sentido positivo para cima (norte) e representado pelo versor $\hat{j}$, sendo que $\left|\hat{j}\right|=1$.

Depois de captar a natureza fundamental dos vetores, você verá que eles têm uma dinâmica especial. Assim como estamos familiarizados com a adição, subtração e multiplicação de números, os vetores também têm um conjunto distinto de operações. Vamos conhecê-las?

Operações com vetores

Para entender plenamente o mundo dos vetores, é crucial abordar o conceito de decomposição de vetores. Vamos utilizar a força como representante das grandezas vetoriais. Imagine que você exerce uma força em um objeto em sua mesa, fazendo-o se deslocar em resposta a essa ação. Visualize essa força $\left(\overrightarrow{F}\right)$  formando um ângulo $\left(\alpha \right)$ com o eixo horizontal e um ângulo $\left(\beta \right)$ com o eixo vertical, como mostra a Figura 4.

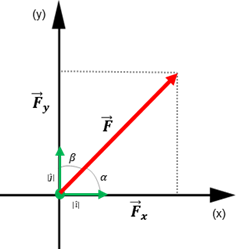
Neste cenário, para conseguirmos identificar as componentes da força $\left(\overrightarrow{F}\right)$ no eixos x e y se faz necessário realizar a decomposição, sendo  $\left({\overrightarrow{F}}_x\right)$ paralela ao eixo das abscissas (eixo x) e $\left({\overrightarrow{F}}_y\right)$ paralelo ao eixo das ordenadas (eixo y).

Denominamos:  ${\overrightarrow{F}}_x= \left|{\overrightarrow{F}}_x\right|\hat{i}$ a projeção horizontal da força $\left(\overrightarrow{F}\right)$ e ${\overrightarrow{F}}_y= \left|{\overrightarrow{F}}_y\right|\hat{j}$ a projeção vertical da força $\left(\overrightarrow{F}\right)$. Assim é possível encontrar os valores por meio da trigonometria. Portanto, analisando a Figura 4: $sen\alpha = \frac{F_y}{F}$; $cos\alpha = \frac{F_x}{F}$; $sen\beta = \frac{F_x}{F}$ e $cos\beta = \frac{F_y}{F}$.

Assim, verificamos que o vetor pode ser composto em duas projeções, no plano, sendo que os módulos dessas projeções podem ser obtidas por $\left|{\overrightarrow{\mathit{F}}}_{\mathit{x}}\right|=\mathit{F}.\mathit{s}\mathit{e}\mathit{n}\mathit{\beta }=\mathit{F}.\mathit{c}\mathit{o}\mathit{s}\mathit{\alpha }$ e $\left|{\overrightarrow{\mathit{F}}}_{\mathit{y}}\right|=\mathit{F}.\mathit{s}\mathit{e}\mathit{n}\mathit{\alpha }=\mathit{F}.\mathit{c}\mathit{o}\mathit{s}\mathit{\beta }$. Para finalizarmos o seu aprendizado sobre a decomposição de vetores, o vetor inclinado pode ser representado por meio das suas projeções. Isto é, seja: $\overrightarrow{\mathit{F}}=\left|{\overrightarrow{\mathit{F}}}_{\mathit{x}}\right|\hat{\mathit{i}}+\left|{\overrightarrow{\mathit{F}}}_{\mathit{y}}\right|\hat{\mathit{j}}$. Ainda pelo teorema de Pitágoras é possível encontrar o módulo do vetor.
Agora, vamos compreender a soma de vetores! Podemos expressar a adição de vetores pela relação vetorial: $\overrightarrow{\mathit{S}}=\overrightarrow{\mathit{A}}+\overrightarrow{\mathit{B}}\mathit{ }$ , sendo $\left(\overrightarrow{S}\right)$ o resultado da combinação dos vetores $\left(\overrightarrow{A}\right)$ e $\left(\overrightarrow{B}\right)$. É essencial estar atento, pois a adição de grandezas vetoriais não é a mesma que a de grandezas escalares. Ao combinar grandezas vetoriais, estamos agregando seus módulos, direções e sentidos. A adição vetorial apresenta duas características fundamentais:

• Propriedade comutativa: a ordem da soma é irrelevante.
• Propriedade associativa: é possível agrupar os vetores em qualquer ordem para somá-los.

Para que você possa compreender, vamos tomar como exemplo a soma de dois vetores. Considere dois vetores $\overrightarrow{\mathbf{A}}$ e $\overrightarrow{\mathit{B}}$. Chamaremos o vetor soma ou resultante, um terceiro vetor denominado de $\overrightarrow{\mathbf{S}}$, que pode ser obtido geometricamente pela Regra do Paralelogramo. Para entender essa regra, imagine que você tem dois vetores (pense neles como setas) começando no mesmo ponto. Para somá-los usando a regra do paralelogramo:

• Desenhe um paralelogramo usando os dois vetores como lados.
• A diagonal desse paralelogramo, começando de onde os vetores começam, é a soma deles!

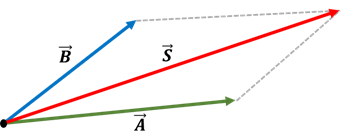
É como se você tivesse duas forças empurrando algo em direções diferentes. A Regra do Paralelogramo mostra qual é a direção e força combinadas desse empurrão! Ainda é possível determinar o módulo do vetor resultante $\left|\overrightarrow{\mathit{S}}\right|$por meio da lei dos cossenos (sinal positivo): ${\left|\overrightarrow{\mathit{S}}\right|}^2={\left|\overrightarrow{\mathit{A}}\right|}^2.{\left|\overrightarrow{\mathit{B}}\right|}^2+2.\left|\overrightarrow{\mathit{A}}\right|.\left|\overrightarrow{\mathit{B}}\right|.\mathit{c}\mathit{o}\mathit{s}\mathit{\theta }$, sendo $\left(\mathit{\theta }\right)$ o ângulo formado entre os vetores $\overrightarrow{\mathit{A}}$ e $\overrightarrow{B}$.  

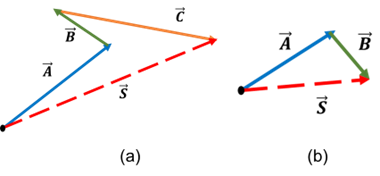
Você já percebeu que os vetores têm sua própria maneira especial de interagir? A primeira, que você já conheceu, é a Regra do Paralelogramo, utilizada para somar dois vetores. Mas e se tivermos mais do que dois vetores para somar? Aí entra a Regra do Polígono! Imagine que você está traçando uma rota em um mapa usando várias setas, uma após a outra. Ao usar a Regra do Polígono, simplesmente colocamos o final de um vetor no começo do próximo. O vetor resultante é aquele que começa no ponto de origem do primeiro vetor e termina na extremidade do último.

Na Figura 6 (a), os vetores $\overrightarrow{\mathit{A}}$, $\overrightarrow{\mathit{B}}$ e $\overrightarrow{\mathit{C}}$ são somados para formar um vetor resultante $\overrightarrow{\mathit{S}}$. Para somar vetores utilizando a Regra do Polígono, colocamos o início de um vetor no final do vetor anterior. Depois de posicionar todos os vetores, o vetor resultante (ou vetor soma) é traçado do ponto de partida do primeiro vetor até o ponto final do último vetor. Utilizando a regra do polígono para realizar a soma de dois vetores, como o caso da Figura 6 (b), é possível determinar o módulo do vetor resultante $\left|\overrightarrow{\mathit{S}}\right|$ por meio da lei dos cossenos (sinal negativo): ${\left|\overrightarrow{\mathit{S}}\right|}^2={\left|\overrightarrow{\mathit{A}}\right|}^2.{\left|\overrightarrow{\mathit{B}}\right|}^2-2.\left|\overrightarrow{\mathit{A}}\right|.\left|\overrightarrow{\mathit{B}}\right|.\mathit{c}\mathit{o}\mathit{s}\mathit{\theta }$, sendo $\left(\mathit{\theta }\right)$ o ângulo formado entre os vetores $\overrightarrow{\mathbf{A}}$ e $\overrightarrow{\mathbf{B}}$.  
A chave para se lembrar aqui é a sequência e a ordem, isso faz toda a diferença quando você está somando vetores. Agora, com essas regras, você está bem equipado para lidar com somas vetoriais, seja qual for o número de vetores envolvidos!

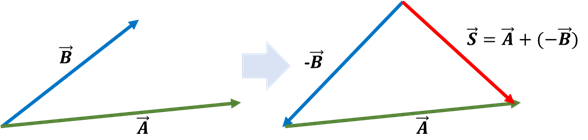
Já a subtração de vetores envolve a determinação de um vetor resultante a partir de dois vetores fornecidos. Para subtrair o vetor $\overrightarrow{\mathit{B}}$ do vetor $\overrightarrow{\mathit{A}}$ (representado como $\overrightarrow{\mathbf{A}}\mathbf{-}\overrightarrow{\mathbf{B}}$):

1. Inverta a direção do vetor $\overrightarrow{\mathit{B}}$: o vetor com direção oposta ao $\overrightarrow{\mathit{B}}$ é chamado de vetor oposto e é denotado como $\mathbf{-}\overrightarrow{\mathbf{B}}$.
2. Adicione o vetor $\overrightarrow{\mathit{A}}$ ao vetor oposto $\mathbf{-}\overrightarrow{\mathbf{B}}$: a subtração de vetores é, portanto, equivalente à adição de um vetor ao oposto de outro. Use a regra da adição de vetores para obter o vetor resultante $\overrightarrow{\mathit{S}}$.

Lembre-se: a subtração de vetores considera tanto magnitude quanto direção.

Ao final desta jornada, esperamos que você tenha conseguido perceber a essência e a relevância das grandezas físicas em nossa vida cotidiana. As unidades, a notação científica, os prefixos e, principalmente, o Sistema Internacional (SI) são ferramentas fundamentais para a nossa comunicação e nosso entendimento preciso do mundo. As grandezas vetoriais e escalares, com suas distinções e propriedades, oferecem uma linguagem única para descrever fenômenos tão variados quanto a brisa suave de uma tarde e a força de um furacão. Que este conceito tenha sido apenas o começo de uma aventura de descobertas e compreensões mais profundas.

Vamos Exercitar?

No início da aula, consideramos a importância das grandezas ao quantificar e compreender o mundo ao nosso redor, como a força e a direção do vento em um dia tempestuoso. É importante saber tanto a magnitude quanto a direção do vento em um dia tempestuoso porque essas informações nos fornecem uma descrição completa do vento. A magnitude do vento nos diz quão forte ele está soprando, enquanto a direção nos indica para onde o vento está se deslocando.

Vimos que não só medimos distâncias, tempos e volumes com unidades específicas, mas também que essas unidades fazem parte de um sistema globalmente aceito: o Sistema Internacional (SI). Esse sistema nos ajuda a ter uma linguagem comum em ciência e tecnologia.

Além disso, exploramos a diferença entre grandezas escalares e vetoriais. Enquanto as primeiras apenas nos dão magnitude (como a temperatura), as vetoriais também nos indicam uma direção e um sentido (como o vento). E o vento em um dia tempestuoso? Ele é representado por uma grandeza vetorial, onde tanto a sua força (magnitude) quanto a direção são cruciais para compreendermos seus efeitos.

Ao descrever o vento como um vetor, podemos realizar operações matemáticas com ele, como soma e subtração de vetores. Isso nos permite determinar a resultante do vento quando há múltiplas forças atuando sobre ele, como em um dia tempestuoso com ventos vindos de diferentes direções. Além disso, as grandezas vetoriais nos permitem visualizar e representar graficamente o vento, facilitando a compreensão e a comunicação das informações. Podemos usar setas para representar a direção e a magnitude do vento em um mapa, por exemplo.

Quanto à notação científica, descobrimos sua utilidade ao lidar com números extremamente grandes ou pequenos, facilitando nossa compreensão e cálculos.

Conhecer tanto a magnitude quanto a direção do vento em um dia tempestuoso é importante para entender completamente o fenômeno. As grandezas vetoriais nos ajudam a representar e compreender essas informações, permitindo-nos realizar cálculos e visualizar graficamente o vento.

Por fim, reflita: em que outras situações do seu dia a dia você poderia aplicar o conhecimento sobre grandezas vetoriais? E como a notação científica pode ser útil em outras áreas do seu aprendizado?

Esta exploração nos ofereceu uma nova perspectiva sobre como entendemos e interagimos com o mundo. Continue questionando, explorando e aplicando seus conhecimentos!

Saiba Mais

Grandezas físicas: unidades, notação científica, prefixos, o sistema internacional (SI)

Você já se perguntou como surgiram as unidades de medida que usamos? Ou como expressar grandezas extremamente grandes ou pequenas de forma mais simples? Descubra isso e muito mais no livro Sistema internacional de unidades. Uma verdadeira viagem pelo universo das grandezas físicas te espera!

INMETRO/CICMA/SEPIN. Sistema Internacional de Unidades: SI.— Duque de Caxias, RJ: INMETRO/CICMA/SEPIN, 2012.

Grandezas vetoriais e escalares e suas diferenças

Vetores e escalares são conceitos fundamentais da física, mas você sabe diferenciá-los? Mergulhe no livro Vetores e Geometria Analítica e afie seus conhecimentos. Uma oportunidade imperdível para aprofundar-se no fascinante mundo vetorial. O livro está disponível na Biblioteca Virtual. 

MACIEL, T. Vetores e geometria analítica: do seu jeito. Editora Blucher, 2022.

Grandezas vetoriais: representação gráfica, módulo, direção e sentido

Representar vetores graficamente é uma habilidade essencial na física. Quer aprender de forma intuitiva e prática? Recomendamos a leitura do Capítulo 1 do livro Física dos autores Cutnell, John, D. e Kenneth W. Johnson. O capítulo aborda de forma lúdica os conceitos vetoriais.

CUTNELL, J. D.; JOHNSON, K. W. Física. 9ª ed. Rio de Janeiro. LTC. 2016.

Operações: adição/subtração e decomposição de vetores

As operações com vetores são a base para muitos fenômenos físicos que observamos no nosso dia a dia. Quer entender como elas funcionam e como aplicá-las? Explore a plataforma GeoGebra, uma ferramenta educativa de matemática que oferece a possibilidade de visualização gráfica de vetores e suas operações.

Referências Bibliográficas

CUTNELL, J. D.; JOHNSON, K. W. Física. 9. ed. Rio de Janeiro: LTC, 2016. v. 1.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: mecânica. 12.ed. Rio de Janeiro: LTC, 2023.

INMETRO. Sistema internacional de unidades - SI. 8. ed. (revisada). Rio de Janeiro, 2007. Disponível em: http://www.inmetro.gov.br/inovacao/publicacoes/si_versao_final.pdf. Acesso em: 28 out. 2023.

INMETRO/CICMA/SEPIN. Sistema Internacional de Unidades: SI. Duque de Caxias, RJ: INMETRO/CICMA/SEPIN, 2012. Disponível em: http://www.inmetro.gov.br/inovacao/publicacoes/si_versao_final.pdf. Acesso em: 1 mar. 2024.

SERWAY, R. A.; JEWET JR, J. W. Física para cientistas e engenheiros: mecânica. 9. ed. São Paulo: Cengage Learning, 2017. v. 1.

Referencial inercial e grandezas da cinemática

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante! A sua compreensão do mundo ao seu redor depende muito do ponto de onde você está observando. Isso nos leva ao conceito de "referencial inercial", um local a partir do qual observamos e descrevemos os movimentos. Além disso, o modo como medimos e interpretamos deslocamentos, velocidades e acelerações também se baseia em nossa compreensão desses referenciais.

Imagine-se a bordo de um trem em movimento. Do lado de fora, vê outro trem passar, mas não consegue dizer se ele está se movendo para frente ou para trás em relação a você. Esse é um dilema clássico de observação e perspectiva. De quem é o movimento que você está observando? Seu trem está indo para trás ou o outro trem está avançando? Essa é a maravilha (e a complexidade) do movimento relativo.

Mas vamos aprofundar mais esse cenário. Digamos que você queira medir a velocidade do outro trem ou determinar sua aceleração. Como você faria isso estando em um trem em movimento? E mais: como o tempo influencia essas medições? Essa é a sua problematização.

Com o que você aprenderá aqui, estará mais apto a decifrar esse enigma e muitos outros relacionados ao movimento. Então, a pergunta que fica é: como a sua perspectiva ou ponto de referência influencia sua interpretação do movimento? Mantenha essa questão em mente enquanto avançamos.

Preparado para embarcar nesta jornada? Vamos lá!

Vamos Começar!

Caro estudante, a cinemática é o ramo da física que estuda o movimento dos corpos, sem se preocupar com as causas desse movimento (as forças envolvidas). Em outras palavras, a cinemática foca no "como" do movimento: como um objeto se move, qual trajetória ele segue, qual sua velocidade ou aceleração, sem se aprofundar no "porquê" desse comportamento. Se você já se perguntou sobre a rapidez com que algo se move, o caminho que percorre ou como sua velocidade muda ao longo do tempo, então estava fazendo perguntas cinemáticas!

Com essa base, podemos mergulhar mais fundo em tópicos específicos da cinemática, como referenciais inerciais e movimento relativo, para entender melhor o intricado mundo do movimento.

Referencial inercial e o movimento relativo

Um referencial inercial é um sistema de referência no qual as leis de Newton da mecânica se mantêm inalteradas. Ou seja, é um "ponto de vista" a partir do qual os objetos que não estão sujeitos a forças externas permanecem em repouso ou se movem em uma linha reta a uma velocidade constante. Em termos simples, um referencial inercial não está acelerando.

Por exemplo, uma pessoa sentada em um carro que viaja em uma estrada plana e reta a uma velocidade constante estaria em um referencial inercial. Se algo cair do carro, o objeto cairá diretamente para baixo. Porém, se o carro fizer uma curva brusca ou acelerar/desacelerar, o objeto não cairá diretamente para baixo. Durante a curva, aceleração ou desaceleração, o carro não serve como um referencial inercial. Portanto, quando o carro (ou qualquer sistema de referência) está sob aceleração e não é um referencial inercial, os objetos dentro desse sistema estarão se movendo de forma relativa ao próprio sistema.

Para uma compreensão mais aprofundada desse conceito, é essencial familiarizar-se com o movimento relativo. O conceito de movimento relativo é fundamental para entender que o movimento de um objeto sempre é observado e descrito em relação a um ponto de referência específico, e este pode estar em movimento.

Imagine dois trens, A e B, viajando lado a lado. Se o trem A se move a 60 km/h e o trem B a 40 km/h na mesma direção, do ponto de vista de um observador em B, o trem A se moverá a apenas 20 km/h em relação a ele. Porém, para um observador parado em uma estação, o trem A está se movendo a 60 km/h e o trem B a 40 km/h. Aqui, vemos claramente como a velocidade de um objeto pode variar dependendo do referencial do observador.

A essência do movimento relativo é que não existe um "estado absoluto de repouso". Tudo se move em relação a algo. O que percebemos como "parado" ou "em movimento" depende totalmente de nosso próprio estado de movimento.

Agora que você aprendeu o referencial inercial e o movimento relativo, é essencial dominar os conceitos de deslocamento, velocidade e aceleração. Esses elementos são os pilares da cinemática, a ciência que nos permite explorar o "como" do movimento.

Deslocamento, a velocidade e a aceleração

Quando olhamos para o movimento de um objeto, às vezes, podemos ou não precisar nos preocupar com o tamanho desse objeto. Um ponto material (ou partícula) é como um objeto super pequenininho, tão pequeno que suas dimensões não fazem diferença quando comparadas com as distâncias que ele percorre. É como se fosse um pontinho que se move.

Agora, se o tamanho do objeto importa, aí estamos falando de um corpo extenso (ou corpo rígido). Isso significa que o objeto tem dimensões significativas e não é apenas um pontinho.

Agora que você sabe a diferença entre um ponto material e um corpo rígido, vamos explorar dois conceitos fundamentais na física que nos ajudam a entender a localização de objetos: a posição e o deslocamento.

A posição de um objeto se refere à localização específica onde ele se encontra em relação a um ponto de referência que escolhemos. Pense nisso como o lugar exato onde o objeto está localizado. Normalmente, nós representamos essa posição por meio de uma coordenada, como uma distância medida a partir de um ponto inicial. Para tornar isso mais claro, imagine que você está medindo a posição de um carro em uma estrada; você poderia descrever essa posição em termos de quilômetros a partir de um ponto de partida. A posição de um ponto material (em um plano) é definida pelo par de coordenadas cartesianas (x; y). Veja, na Figura 1, as posições das partículas A, B, C.

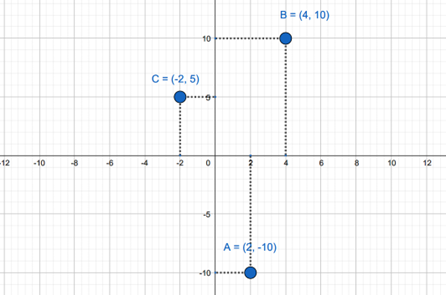
O deslocamento, por outro lado, é uma grandeza vetorial que nos ajuda a entender como a posição de um objeto muda com o tempo. Em termos simples, ele nos diz qual é a diferença na posição de um objeto entre o ponto em que ele começou e o ponto onde ele terminou. É uma combinação de distância e direção. Para ficar mais claro, se um carro começou em 0 km em uma estrada e depois se moveu em linha reta até 100 km, seu deslocamento seria de 100 km na direção da viagem.

Quando estamos estudando a posição de uma partícula na cinética, o primeiro passo é definir um eixo que represente o seu movimento linear. Escolhemos um ponto de partida nesse eixo, que chamamos de ponto de origem, frequentemente referido como ponto $\mathrm{O}$. A partir desse ponto de origem, analisamos o movimento da partícula em si. A partir do ponto $\mathrm{O}$, calculamos a posição "s" da partícula, e a quantidade pela qual essa partícula se move é chamada de deslocamento  no eixo. Esse conceito está representado na Figura 2.

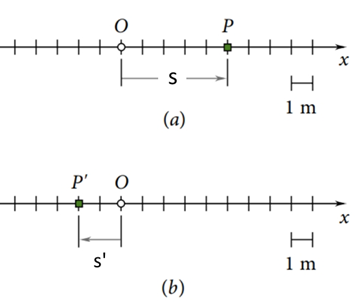
É importante destacar que o deslocamento é um vetor desenhado da posição inicial para a posição final, ou seja, é como um tipo especial de medida que tem duas direções diferentes. Para tornar as coisas mais fáceis, decidimos escolher uma direção como positiva. Quando um objeto se move nessa direção positiva, seu deslocamento é considerado positivo.

Então, se decidirmos que a direção para a direita é a nossa direção positiva, o deslocamento de O para P é um número positivo, como visto na Figura 2 (a). Por outro lado, se o objeto se mover na direção oposta, seu deslocamento será negativo. Por exemplo, o deslocamento de O para P’ é negativo, sendo o caso da Figura 2 (b).

O deslocamento é calculado pela diferença entre onde um objeto está agora e onde ele estava antes. Usamos o símbolo $∆$ (letra grega maiúscula "delta") para representar essa diferença.

Assim, o deslocamento pode ser calculado de acordo com a Equação (1). Sendo, ${\mathit{S}}_{\mathbf{f}}$ = espaço (posição) final e ${\mathit{S}}_{\mathbf{i}}\mathbf{ }$= espaço (posição) inicial.

$\mathrm{\Delta }\overrightarrow{S}= {\overrightarrow{S}}_f-{\overrightarrow{S}}_i$      (1)

Ao olharmos o movimento da partícula e escolhermos momentos específicos para cada lugar onde a partícula está, conseguimos descobrir algo chamado de "velocidade média". Pense nisso como um valor geral que não muda enquanto a partícula se move. É como quando você está viajando de carro e quer saber o quão rápido está indo. Você olha para o tempo que passou desde o início da viagem e a distância que percorreu até agora. A velocidade média é como a média de quão rápido você estava indo durante toda a viagem, mesmo que tenha acelerado ou diminuído a velocidade em alguns momentos.

Então, na física, ao analisarmos o movimento de uma partícula e escolhermos momentos específicos para medir sua posição, podemos calcular essa velocidade média, que nos dá uma ideia geral de quão rápido ela está indo durante todo o trajeto. Assim, por definição, a velocidade média é a taxa de mudança do deslocamento de um objeto em relação ao tempo e o vetor velocidade média é um vetor que aponta na mesma direção e no mesmo sentido que o deslocamento. Para calcular a velocidade média, você divide o deslocamento total pelo tempo decorrido, como pode ser visto na Equação (2). Sendo, ${\mathit{S}}_{\mathbf{f}}$ = espaço (posição) final no tempo final considerado ($t_f$) e ${\mathit{S}}_{\mathbf{i}}$ = espaço (posição) inicial no tempo inicial considerado (${\mathit{t}}_{\mathbf{i}}$).

${\overrightarrow{v}}_{méd}=\mathrm{ }\frac{\mathrm{\Delta }\overrightarrow{S}}{\mathrm{\Delta t}}= \frac{ {\overrightarrow{S}}_f-{\overrightarrow{S}}_i \mathrm{ }}{t_f-t_i}$      (2)

A equação da velocidade média indica a rapidez média com que um objeto se move entre dois pontos em um determinado intervalo de tempo. A unidade típica para velocidade é quilômetros por hora (km/h) ou metros por segundo (m/s).

Siga em Frente...

Velocidade e aceleração instantâneas

Agora, imagine que você está observando um pássaro voando e quer descobrir exatamente o quão rápido ele está voando em um determinado ponto de seu voo. Essa "foto rápida" da velocidade do pássaro em um momento específico é o que chamamos de "velocidade instantânea".

Para descobrir essa velocidade, precisamos olhar para um espaço de tempo muito curto. Neste caso, as mudanças no tempo ($\Delta t$) e no deslocamento do pássaro ($\Delta s$) são tão mínimas que se aproximam de zero. Assim:

$\overrightarrow{v}=\underset{\mathrm{\Delta t}\to 0}{\lim }\frac{\mathrm{\Delta }\overrightarrow{S}}{\mathrm{\Delta t}}$

Ao observar a equação proposta, quando o intervalo de tempo se aproxima de um valor muito próximo a zero, deixamos de considerar o deslocamento e focamos em uma posição específica do movimento. Com isso, podemos estabelecer a relação da velocidade instantânea por meio da derivada do deslocamento em relação ao tempo da seguinte maneira:

$\overrightarrow{v}=\mathrm{ }\frac{\mathrm{d}\overrightarrow{S}}{\mathrm{dt}}$      (3)

Aqui vai um ponto importante que você deve compreender, imagine que você está olhando para uma linha reta, que chamaremos de "eixo do deslocamento". Nessa linha, há uma origem, que é o ponto $\mathrm{O}$, e um sentido, que vai da esquerda para a direita.

O deslocamento de um objeto (como uma partícula) nessa linha pode ser para a direita ou para a esquerda. A direção desse deslocamento é mostrada pelo sinal de $∆S$.

Aqui vem a parte interessante: a velocidade também tem um sinal, e ele nos dá uma dica sobre para onde a partícula está indo. Como o tempo sempre é positivo (o relógio sempre anda para frente!), é o sinal do deslocamento que vai nos dizer o sinal da velocidade.

• Se a velocidade tem sinal positivo, a partícula está se deslocando para a direita.
• Se a velocidade tem sinal negativo, a partícula está indo da direita para a esquerda.

Então, só de olhar para o sinal da velocidade já sabemos a direção do movimento da partícula!

Agora, imagine um carro na estrada. Às vezes, ele aumenta a velocidade, às vezes diminui e, em outros momentos, mantém a velocidade por um tempo. A aceleração é como o "controlador de velocidade" desse carro.

• Se o carro está aumentando a velocidade, ele está "acelerando". A aceleração está ajudando o carro a ir mais rápido.
• Se o carro está diminuindo a velocidade, a aceleração está trabalhando contra ele, como se estivesse pisando no freio. Nesse caso, chamamos o movimento de "retardado".
• E se o carro estiver mantendo a mesma velocidade, a aceleração é zero. É como se o carro estivesse no "piloto automático".

Então, a aceleração nos mostra como a velocidade do carro (ou de qualquer objeto) está mudando. Pode ser positiva, ajudando o movimento, ou negativa, indo contra o movimento.

Lembre-se: Aceleração positiva = carro acelerando. Aceleração negativa = carro desacelerando. Aceleração zero = velocidade constante.

De modo simplificado, existem dois tipos de aceleração quando estudamos as partículas, a aceleração média e a aceleração instantânea. A aceleração média indica como a velocidade de um objeto varia ao longo do tempo. Ela nos mostra com que rapidez a velocidade desse objeto se altera em um período de tempo determinado. Normalmente, usamos a unidade metros por segundo ao quadrado (m/s²) para expressá-la e ela pode ser descrita pela Equação (4):

${\overrightarrow{a}}_m=\frac{\Delta v}{\Delta t}$      (4)

Já a aceleração instantânea é a aceleração de um objeto em um ponto específico no tempo. Assim como a velocidade instantânea, representa a aceleração exata do objeto em um momento particular e pode variar ao longo do tempo. É possível determiná-la com a Equação (5):

$\overrightarrow{a}=\underset{\Delta t\to 0}{lim}\frac{\Delta v}{\Delta t} \to a ⃗=dv/dt$      (5)

Assim como a Equação (3) indica que a velocidade instantânea (escalar) de um objeto/partícula é definida como a derivada do deslocamento em função do tempo, a Equação (5) mostra que a aceleração instantânea (escalar) de um objeto/partícula é definida como a derivada da velocidade em função do tempo.

Vamos Exercitar?

Um referencial inercial é um ponto ou sistema de referência no qual as leis da física, especialmente a mecânica, são observadas para serem constantes e não aceleradas. No nosso dilema dos trens, cada trem pode ser considerado um referencial inercial em relação ao outro. Entretanto, em um contexto mais amplo, quando observamos o movimento de planetas, estrelas ou satélites, a Terra não é um referencial inercial perfeito, pois ela mesma está em movimento e sujeita a forças como a gravidade.

Imagine que o trem está a 100 km de uma estação e o outro trem, que você observa, está a 110 km. Isso é a posição absoluta de cada trem. No entanto, a posição relativa do outro trem em relação a você é apenas de 10 km. O deslocamento, por sua vez, é a mudança na posição e é vetorizado, ou seja, tem magnitude e direção. Já velocidade média é calculada considerando a distância total percorrida dividida pelo tempo total.

No caso do trem, se ele percorreu 100 km em 2 horas, sua velocidade média foi de 50 km/h. A velocidade instantânea é a velocidade em um ponto específico no tempo, como um velocímetro de um carro mostrando a velocidade atual. Já a aceleração se refere à taxa de mudança da velocidade. Se o trem foi de 0 a 50 km/h em 10 segundos, sua aceleração média foi de 5 km/h por segundo.

Como a velocidade e aceleração podem mudar ao longo do tempo, podemos representá-las como funções do tempo. Por exemplo, um trem acelerando pode ter uma equação de aceleração a(t) que nos diz como sua aceleração varia em diferentes momentos.

E agora, voltando ao nosso dilema inicial dos trens: com o que você aprendeu, se ambos os trens estiverem se movendo a 50 km/h, mas em direções opostas (um em relação ao outro), eles parecerão estar se movendo a 100 km/h um em relação ao outro. A sua percepção de movimento depende do seu referencial!

Caro estudante, concluímos nossa jornada pelos intrigantes conceitos de Referencial Inercial, Movimento Relativo, entre outros aspectos fundamentais da física. Exploramos as nuances entre velocidades e acelerações, sejam elas médias ou instantâneas, e como elas se relacionam com o tempo. Esperamos que este material tenha enriquecido seu entendimento e despertado a curiosidade para continuar investigando e aprendendo. A física é um campo vasto e sempre há mais a descobrir. Desejamos sucesso em seus estudos futuros e lembre-se: o conhecimento é uma jornada contínua. Até a próxima!

Saiba Mais

Referencial inercial e o movimento relativo

Você já se questionou sobre como interpretamos o movimento? Aquilo que nos parece estático pode estar em movimento para outro observador. Convidamos você a se aprofundar no instigante universo dos referenciais inerciais e descobrir como o movimento é percebido de maneira relativa. Além das informações que compartilhamos aqui, recomendamos uma aula extra que trabalha o conteúdo de forma descomplicada.

IMD - INSTITUTO METRÓPOLE DIGITAL. O movimento é relativo. [s. d.]

Posição, deslocamento, velocidade e aceleração

Essas grandezas são fundamentais para a descrição do movimento. Se você deseja aprofundar seus conhecimentos sobre esses conceitos, temos uma ótima dica para você! Dê uma olhada no Capítulo 2, especialmente nas seções 2.1 a 2.3, do livro Fundamentos de Física, escrito por Halliday, Resnick e Walker. É uma leitura bastante popular em cursos introdutórios de física e traz explicações bem didáticas, além de exemplos práticos sobre posição, deslocamento, velocidade e aceleração. Tenho certeza de que será de grande ajuda! O livro está disponível na Biblioteca Virtual.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

Velocidade e aceleração instantânea

Para explorar mais profundamente esse tópico, confira:

Livro: já imaginou como a velocidade e a aceleração variam com o passar do tempo? Esse conceito é fundamental para entender muitos fenômenos ao nosso redor. Convidamos você a explorar este tópico e descobrir sua aplicação em nosso cotidiano. Para aprofundar sua compreensão, recomendamos a leitura do Capítulo 2 do livro Curso de Física Básica, de Nussenzveig Herch Moysés. Uma obra rica que certamente enriquecerá seu entendimento sobre o tema. O livro está disponível na Biblioteca Virtual.

NUSSENZVEIG, H. M. Curso de Física Básica. Editora Blucher, 2013.

Recursos on-line: existem muitos recursos on-line interativos que podem ajudar a visualizar a velocidade e a aceleração. Websites de educação em física, como o PhET Interactive Simulations, oferecem simulações envolventes que podem ajudar a aprofundar seu entendimento desses conceitos dinâmicos.

Referências Bibliográficas

BEER, F. P.; JOHNSTON JR., E. R.; CORNWELL, P. J. Mecânica vetorial para engenheiros: Dinâmica. 9. ed. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

HIBBELER, R. C. Dinâmica: mecânica para engenharia. 14. ed. São Paulo: Pearson, 2017.

MERIAM, J. L.; KRAIGE, L. G.; BOLTON, J. N. Mecânica para engenharia: Dinâmica. 9. ed. Rio de Janeiro: LTC, 2022.

Movimento em uma dimensão

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la?
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

A jornada da cinemática é fascinante e repleta de nuances. Hoje, vamos abordar alguns dos movimentos mais comuns que observamos no nosso dia a dia, mas que, sob a lente da física, revelam complexidades e padrões interessantes. Começaremos com o Movimento Retilíneo Uniforme (MRU), onde objetos se movem em uma linha reta a uma velocidade constante. Já pensou em um carro se movendo em uma estrada reta sem acelerar nem frear? Isso é MRU!

Em seguida, avançaremos para o Movimento Retilíneo Uniformemente Variado (MRUV), que introduz uma nova camada de complexidade, considerando a aceleração. Por fim, nos aprofundaremos em fenômenos fascinantes: a Queda Livre e o Lançamento Vertical. Já se perguntou por que todos os objetos caem na mesma velocidade em um vácuo, independentemente de sua massa?

Se você jogar uma bola verticalmente para cima, em que ponto ela terá a maior aceleração? E qual será a velocidade dela no ponto mais alto de sua trajetória?

Prepare-se para desvendar esses mistérios e aplicar seus conhecimentos em situações práticas!

Vamos Começar!

Prezado estudante, a cinemática é como um segmento da Mecânica focado em detalhar movimentos usando medidas relacionadas à distância e duração. Estabelecemos fundamentos dos movimentos com base nas concepções de velocidade e aceleração médias.

Nesta discussão, voltamos nossa atenção para circunstâncias em que tanto a velocidade quanto a aceleração, quando presentes, são constantes. Em termos simples, nos referiremos a elas apenas como velocidade e aceleração.

Um ponto crucial a se observar é nossa menção ao Movimento Retilíneo Uniforme (MRU) e ao Movimento Retilíneo Uniformemente Variado (MRUV). "Retilíneo" se refere a movimentos em linha reta. Entretanto, na realidade, nem todas as trajetórias são perfeitamente retas. A ideia é usar o MRU como um padrão de referência, independentemente da real forma da trajetória.

Movimento Retilíneo Uniforme (MRU)

Imagine uma rodovia com segmentos retos e curvas. O carro tem liberdade total de movimento? Podemos considerar o movimento do carro como retilíneo?

Anteriormente, discutimos a ideia de velocidade média, que representa a distância média percorrida por um objeto em movimento ao longo do tempo. Como ilustração, se um objeto se move 10 m em 50 segundos em uma esteira retilínea, sua velocidade média é 0,2 m/s. Ao reduzir o intervalo de tempo da análise, nos aproximamos da real velocidade do objeto em um dado momento, ou velocidade instantânea. Tomando o exemplo da esteira, o objeto movia-se a uma velocidade constante de 0,2 m/s, caracterizando um MRU. Em termos cinemáticos, a velocidade pode ser representada por uma função do tempo: v(t).

Nos estudos de Física, fenômenos são traduzidos em linguagem matemática. Tomando como exemplo o Movimento Retilíneo Uniforme (MRU), podemos representar a posição de um objeto ao longo do tempo através de uma função linear, conhecida como equação horária da posição, representada pela Equação (1). Essa função é derivada da concepção da velocidade média.

$v_{m\mathrm{é}d}=v= \frac{\mathrm{\Delta }s}{\mathrm{\Delta t}}$

$v=\mathrm{ }\frac{ \mathrm{ }{S}_f-\mathrm{ }{S}_0 \mathrm{ }}{t_f-t_i}$

Considerando o tempo inicial ($t_i$) igual a zero é possível chegar à função horária da posição:

$\left(t\right)=s_0+vt$      (1)

Sendo: $\mathit{s}\mathbf{\left(}\mathit{t}\mathbf{\right)}\mathbf{ }$a posição do corpo no tempo (t); ${\mathit{s}}_{\mathbf{0}}$ é a posição inicial do corpo (sua posição no tempo $t_i = 0$);  é a velocidade constante do corpo no MRU e $\mathit{t}$ é o tempo decorrido desde $t_i$.

A análise gráfica é essencial em alguns casos, fornecendo importantes informações, vamos analisar a Figura 1 a seguir:

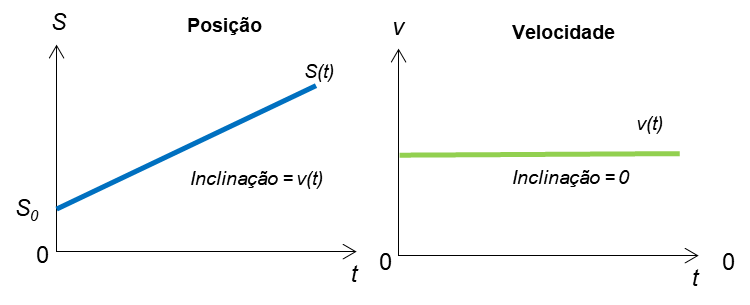
No gráfico que representa a posição, a inclinação constante indica uma velocidade constante ao longo do tempo. O fato de ser uma linha reta indica que o objeto se desloca com uma velocidade uniforme, sem aceleração. A inclinação da linha fornece a magnitude da velocidade do objeto. Se verificarmos o gráfico da velocidade, por ele ser paralelo ao eixo do tempo, indica que a velocidade do objeto é constante e não varia com o tempo. A altura da linha verde em relação ao eixo de velocidade fornece a magnitude da velocidade, que é constante durante todo o movimento.

Além disso, se verificarmos o gráfico da velocidade, note que a área abaixo da linha verde monta um retângulo, se calcularmos a área desse retângulo é possível determinar o deslocamento conhecendo apenas o gráfico. Ao analisar o gráfico da velocidade, é possível observar que a área sob a linha verde forma um retângulo. A magnitude dessa área não representa apenas um mero detalhe gráfico, mas tem um significado físico: ela indica o deslocamento do objeto durante o intervalo de tempo considerado.

Portanto, ao calcular a área desse retângulo no gráfico da velocidade versus tempo, obtemos diretamente o valor do deslocamento do objeto, permitindo-nos compreender o movimento do corpo apenas com base nessa representação visual.

Após compreendermos profundamente o Movimento Retilíneo Uniforme (MRU), onde a velocidade se mantém constante e a aceleração é nula, é hora de avançarmos em nossos estudos para um cenário mais dinâmico. No MRUV, ou Movimento Retilíneo Uniformemente Variado, não só observamos a trajetória em linha reta, mas também nos deparamos com uma variação constante da velocidade devido à presença de uma aceleração constante.

Movimento Retilíneo Uniformemente Variado (MRUV)

No estudo do movimento, dois conceitos cruciais se destacam: a velocidade e a aceleração. Ambos desempenham um papel fundamental na descrição e análise do comportamento dos objetos em movimento, mas o que acontece quando eles não são constantes? Quando a velocidade e a aceleração não seguem um caminho linear, mergulhamos no intrigante mundo da aceleração e velocidade em função do tempo.

A aceleração, como já sabemos, mede como a velocidade de um objeto muda ao longo do tempo. É uma peça essencial para compreendermos a dinâmica de carros, aviões, planetas e até mesmo partículas subatômicas. Mas quando a aceleração em si não é uma constante, quando varia de acordo com o tempo, o cenário se torna ainda mais fascinante e desafiador.

Juntamente com a aceleração, a velocidade é outra grandeza que desempenha um papel fundamental. Ela nos fornece informações sobre a rapidez com que um objeto se desloca em relação ao tempo. E quando a velocidade também está sujeita a mudanças ao longo do tempo, nossa compreensão do movimento se torna mais rica e complexa. Sabendo que ambas variam em relação ao tempo, podemos descrever a aceleração em função da posição, ou seja, com uma derivada de segunda ordem:

$a=\frac{d}{dt}\left(v\right)=\frac{d}{dt}\left(\frac{ds}{dt}\right)=\frac{d{s}^2}{d{t}^2}$        (2) 

Sendo $\mathit{s}\mathbf{ }$o deslocamento da partícula ou objeto de estudo. Uma maneira mais simples de entender como a velocidade e a aceleração se relacionam com o tempo e com o deslocamento é relacioná-los com o conceito de derivada ou relacionando taxa de variação em relação ao tempo. A velocidade pode ser definida como a derivada da posição em relação ao tempo, como visto a seguir:

$\dot{s}=v=\frac{ds}{dt}$       (3)

Já a aceleração é a derivada de primeira ordem da velocidade em função do tempo ou a derivada de segunda ordem da posição em função do tempo, em ambos os casos ela expressa a taxa de variação da velocidade em relação ao tempo:

$\ddot{s}=a=\frac{dv}{dt}=\frac{d^{2}s}{d{t}^2}$       (4)

Vamos entender melhor com um exemplo prático! Se observarmos como uma partícula se move em linha reta, podemos ver e entender sua posição, velocidade e aceleração em diferentes momentos desse movimento. Assim, se temos uma partícula andando em linha reta e sua posição é mostrada pela equação: $s=5+8t+4t^2-2t^3$, podemos definir a velocidade e a aceleração da partícula ao longo da sua trajetória. Partindo pela determinação da velocidade, definimos que:

$\dot{s}=\mathrm{ }v=\frac{ds}{dt}=\frac{d}{dt}\left(5+8t+4t^2-2t^3\right)$

$\dot{s}=\mathrm{ }v=0+8.1+4.2t-2.3t^2$

$\dot{s}=\mathrm{ }v=8+8t-6t^2$       (5)

E a aceleração é definida ao derivar a velocidade em função do tempo da seguinte forma:

$\ddot{s}=a=\frac{dv}{dt}\left(8+8t-6t^2\right)$

$\ddot{s}=a=0+8.1-6.2t$

$\ddot{s}=a=8-12t$       (6)

Se quisermos determinar a velocidade e a aceleração no instante de tempo t = 2 segundos, basta fazermos a substituição direta do valor nas respectivas equações. Com esse método, torna-se uma tarefa acessível identificar a velocidade ou aceleração precisamente no momento de tempo desejado. Em outras palavras, estamos aprendemos uma ferramenta que nos permite "congelar" o tempo e examinar com precisão quão rápido um objeto está se movendo ou como sua taxa de mudança de velocidade evolui em um instante específico. Isso é particularmente útil quando lidamos com movimentos complexos e variáveis, nos quais a velocidade e a aceleração não são constantes e podem flutuar ao longo do tempo.

Siga em Frente...

No Movimento Retilíneo Uniformemente Variado (MRUV), a variação da velocidade é constante devido à presença de uma aceleração também constante. A relação entre a velocidade de um corpo e o tempo é expressa pela função horária das velocidades, $v\left(t\right)$. Essa função, que é de primeiro grau, traduz como a velocidade de um objeto varia a cada instante de tempo. Matematicamente, essa relação é descrita pela Equação (8):

$a_m= a=\frac{\Delta v}{\Delta t}=\frac{v-v_0}{t-t_0}$       (7)

Considerando o tempo inicial $\left(t_i\right)$ igual a zero é possível chegar à função horária das velocidades:

$v\left(t\right)={v\mathrm{}}_0+a.t$       (8)

Sendo: $\mathit{v}\left(\mathit{t}\right)$ a velocidade do corpo em um instante t, ${\mathit{v}\mathbf{}}_0$ a velocidade inicial do corpo no início do movimento, $\mathit{a}$ a aceleração média (sendo constante), $\mathit{t}$ o tempo decorrido. A partir dessa expressão, pode-se perceber como a aceleração média influencia diretamente na variação da velocidade do corpo ao longo do tempo.

Assim, como visto no MRU, a análise gráfica do Movimento Retilíneo Uniformemente Variado (MRUV) também é fundamental para compreender a natureza desse movimento e suas peculiaridades. No MRU, focamos na relação constante entre deslocamento e tempo. Já no MRUV, a aceleração constante introduz uma complexidade adicional, fazendo com que a velocidade do corpo varie linearmente com o tempo. Vamos analisar a Figura 2, que representa graficamente o MRUV.

Diferentemente do MRU, o gráfico da posição em função do tempo para o MRUV é uma parábola. A concavidade da parábola nos indica o sentido da aceleração: se voltada para cima, indica aceleração positiva, e se voltada para baixo, indica aceleração negativa.

Já o gráfico de velocidade em função do tempo é uma reta inclinada. Isso ocorre porque a aceleração, que é a taxa de variação da velocidade, é constante. A inclinação dessa reta é justamente o valor da aceleração. Se a reta é ascendente (inclinada para cima), indica que a velocidade está aumentando com o tempo, ou seja, temos uma aceleração positiva. Se a reta é descendente (inclinada para baixo), a velocidade está diminuindo com o tempo, indicando uma aceleração negativa.

Outro aspecto interessante deste gráfico é que a área sob a reta (seja ela acima ou abaixo do eixo do tempo) representa o deslocamento do corpo durante aquele intervalo de tempo. Por exemplo, se tivermos um retângulo formado pela reta de velocidade, o eixo do tempo e as linhas verticais que representam o tempo inicial e final, a área desse retângulo nos dá o deslocamento total. Observe também que o gráfico da velocidade versus tempo geralmente forma um trapézio quando o a velocidade inicial não é nula, ou seja, o corpo não está em repouso. Agora, quando verificamos os casos em que a velocidade inicial é zero, a área abaixo do gráfico se forma um triângulo. Partindo da análise onde ${v\mathrm{}}_0\ne 0$, podemos determinar a segunda função horária do deslocamento, por meio da área do trapézio:

$S=Área do trapézio=\frac{\left(Base maior.Base menor\right).Altura}{2}$

$\Delta S=\frac{\left(v+v_0\right)}{2}\cdot t$

Levando em conta que $\Delta S= S-S_0$ e  $v={v\mathrm{}}_0+a.t$, então:

$S-S_0=\frac{\left(v+at+v_0\right)t}{2}$

Portanto, a segunda função horária do deslocamento é representada pela Equação (9):

$s\left(t\right)=s_0+v_{0}t+\frac{a}{2}{t}^2$       (9)

Certamente, até agora, você percebeu que o tempo (t) tem sido um protagonista em nossas discussões sobre movimento. Mas e se nos depararmos com uma situação em que o tempo se torna o grande mistério? Para tais momentos temos uma ferramenta poderosa chamada Equação de Torricelli. Essa equação é uma das equações fundamentais da cinemática e nos permite desvendar os segredos do movimento de um objeto em aceleração constante, mesmo quando o tempo permanece oculto. É como um quebra-cabeça especial que conecta a velocidade inicial, a velocidade final, a aceleração e o deslocamento, tudo sem a necessidade de saber a duração do movimento. Para podermos determinar essa equação, temos que fazer uso das Equações (2) e (3), buscando remover a variável tempo (t). No fim deste processo determinamos a Equação de Torricelli (10).

$v^2=v_0^2+2.a.\Delta s$       (10)

Ela relaciona a velocidade final $\left(v\right)$, a velocidade inicial ​${(v}_0)$, o deslocamento $\left(\Delta s\right)$  e a aceleração $\left(a\right)$ de um objeto em MRUV, sem a necessidade de se conhecer o tempo que esse movimento leva para ocorrer.

Agora que mergulhamos profundamente nas nuances do Movimento Retilíneo Uniformemente Variado (MRUV) e entendemos sua representação gráfica, suas equações e sua aplicabilidade, estamos prontos para explorar outro aspecto fascinante da cinemática: a queda livre e o lançamento vertical. Esses movimentos, influenciados predominantemente pela aceleração da gravidade, revelam comportamentos únicos e proporcionam uma compreensão profunda da interação dos corpos com o campo gravitacional terrestre.

Queda livre e lançamento vertical

Você já soltou algo e viu cair? É a Terra "chamando" os objetos para ela! Esse fenômeno é o que chamamos de queda livre. Tudo cai por causa de um "puxãozinho" da Terra que a gente conhece por gravidade. Seja uma pena ou um elefante de pelúcia (sem ar atrapalhando), eles caem na mesma rapidez. Esse "puxãozinho" é conhecido como a aceleração da gravidade.

Agora, em vez de só soltar, que tal jogar algo para cima? Ao fazer isso, estamos brincando com o lançamento vertical. O objeto sobe, dá uma paradinha no ar e depois? Ele volta, fazendo aquela queda livre que já falamos. Então, lembre-se:

• Queda livre: é a Terra "chamando" os objetos de volta.
• Lançamento vertical: somos nós desafiando a gravidade ao jogar algo para cima, mas, no final, a gravidade sempre ganha e traz tudo de volta.

Ambos são formas de ver a gravidade em ação. E adivinhe? A física nos ajuda a entender como esses movimentos acontecem! Vamos compreender esses movimentos.

A queda livre refere-se ao movimento de um corpo que é solto a partir de uma certa altura e cai exclusivamente sob a influência da gravidade, desconsiderando-se os efeitos do ar (como resistência ou arrasto). Nesse cenário, todos os corpos, independentemente de sua massa, caem com a mesma aceleração – a aceleração da gravidade.

A aceleração da gravidade (geralmente representada por $g⃗=9,81m⁄s^2$) varia ligeiramente em diferentes partes da Terra, mas, para fins de simplificação em muitos problemas, é considerada aproximadamente (no sentido para baixo) ao nível do mar.

Considerando o sentido positivo para baixo, as equações da posição, da velocidade e de Torricelli para de um objeto em queda livre, a partir do repouso, em função do tempo, são respectivamente:

$s\left(t\right)=\frac{g}{2}{t}^2$          (11)

$v\left(t\right)=g.t$           (12)

$v^2=2.g.\Delta s$       (13)

Uma consideração importante é que o deslocamento é a altura (H) de que o copo saiu do repouso, portanto é valido realizar essas análises, tudo bem?

Agora, em vez de soltar a maçã, imagine jogá-la para cima. O que acontece? Ela sobe, desacelera até parar por um instante e depois começa a cair de novo. Esse jogar para cima é o que chamamos de lançamento vertical. Portanto, quando um objeto é lançado verticalmente para cima, ele inicialmente tem uma velocidade inicial $\left(v_0\right)$ contrária à aceleração da gravidade. À medida que sobe, essa velocidade diminui até se tornar zero no ponto mais alto da trajetória. A partir daí, o objeto começa a cair, acelerando devido à gravidade, realizando um movimento de queda livre. Assim, a equação para a posição de um objeto lançado verticalmente e a equação para a sua velocidade, considerando o sentido positivo para cima, são respectivamente:

$s\left(t\right)=v_{0}t-\frac{g}{2}{t}^2$       (14)

$v\left(t\right)=v_0-\mathrm{g}.t$           (15)

É importante notar que, na queda livre e no lançamento vertical, a aceleração é a aceleração da gravidade, ou seja, constante e igual a $\overrightarrow{g}=\mathrm{9,81}\mathrm{ }m/s^2$. No entanto, enquanto na queda livre o corpo começa do repouso (velocidade inicial é zero), no lançamento vertical ele tem uma velocidade inicial que não é zero.

Caro estudante, ao encerrarmos esta aula esperamos que você tenha uma compreensão mais aprofundada da maneira como objetos se movimentam e das forças que atuam sobre eles. Seja uma simples bola lançada ao ar ou um carro em uma ladeira, as leis da física estão sempre em ação, governando os movimentos que observamos no dia a dia. Cada situação apresentada aqui serve como uma janela para um universo mais amplo de conhecimento. Continue investigando, praticando e aplicando seus conhecimentos em situações reais, pois a física está em todo lugar e sua curiosidade é a chave para desvendar seus mistérios. Até a próxima!

Vamos Exercitar?

Caro estudante, quando você joga uma bola verticalmente para cima, ela está, na verdade, enfrentando a aceleração da gravidade durante todo o seu movimento. Assim, a aceleração da bola é constante e igual à aceleração da gravidade (negativa quando jogada para cima e positiva quando cai) e tem seu valor máximo na Terra, aproximadamente 9,81 m/s².

Quanto à sua velocidade no ponto mais alto, ela é temporariamente 0 m/s, pois a bola interrompe seu movimento ascendente e se prepara para começar sua descida.

Para aprofundar seus conhecimentos: calcule o tempo que uma bola leva para alcançar o ponto mais alto quando é lançada verticalmente para cima com uma velocidade inicial de 10 m/s.

Solução: no ponto mais alto, a velocidade da bola é 0 m/s porque ela parará momentaneamente antes de começar a cair novamente. Usando a fórmula da cinemática para movimento uniformemente acelerado:

$v=v_0-gt$

$0=10-\mathrm{9,81}t$

$t=\frac{10}{\mathrm{9,81}}$

$t\approx \mathrm{1,02} s$

Portanto, a bola leva aproximadamente 1,02 segundos para alcançar o ponto mais alto.

• Descreva como seria o movimento de um carro que está em MRUV, considerando uma aceleração constante. Em que situações práticas podemos observar esse tipo de movimento?

Solução: no Movimento Retilíneo Uniformemente Variado (MRUV), o carro não mantém uma velocidade constante. Em vez disso, sua velocidade aumenta ou diminui a uma taxa constante devido à aceleração constante. Se a aceleração for positiva, o carro ganhará velocidade ao longo do tempo; se for negativa, o carro perderá velocidade. O MRUV é caracterizado por uma variação linear da velocidade em função do tempo.

Situações práticas:

• Acelerando de um sinal verde: quando um carro começa a se mover a partir do repouso em um semáforo e acelera constantemente.
• Freando até parar: se um carro estiver em movimento e o motorista aplicar os freios de forma constante até o carro parar.
• Descida ou subida de uma ladeira: em uma ladeira íngreme, um carro pode acelerar (descendo) ou desacelerar (subindo) devido à força gravitacional, mesmo sem pressionar o acelerador ou os freios.

Caro estudante, você acabou de explorar os fundamentos do movimento e as leis que o regem, mas lembre-se de que esse é apenas o início de uma jornada fascinante pelo universo da física. A cada experimento, cálculo ou situação prática que você analisa, há sempre algo mais para aprender e descobrir. Encorajamos você a não parar por aqui. Mergulhe mais fundo, questione, experimente e amplie seus horizontes.

Saiba Mais

Movimento Retilíneo Uniforme (MRU)

O Movimento Retilíneo Uniforme é um conceito fundamental na cinemática. No episódio sobre MRU do podcast Física Dinâmica - Com André Paranaguá, você terá a oportunidade de explorar esse tópico de forma envolvente e dinâmica. André Paranaguá, com sua vasta experiência e maneira única de ensinar, traz insights e explicações claras sobre o assunto, facilitando a compreensão e tornando o aprendizado mais prazeroso. Para você estudante, este episódio é altamente recomendado para ampliar seus horizontes e solidificar seu entendimento sobre o MRU. Incentivamos que você ouça este episódio para aprofundar seus conhecimentos e se conectar com a física de uma forma mais interativa e contemporânea.

Movimento Retilíneo Uniformemente Variado (MRUV)

Recomendamos o artigo acadêmico de acesso aberto dos autores Vivian Menezes; Angelo Ribeiro, Júlia Techio e Sonia Reviliau Movimento Retilíneo Uniformemente Acelerado: Uma proposta de experimento de baixo custo. Esse artigo oferece uma abordagem prática, sugerindo um experimento simples e acessível, mas eficaz, que permite a observação desse tipo de movimento. Ao utilizar materiais de baixo custo, como um arame e uma miçanga, ele demonstra que a experimentação em física não necessita de equipamentos caros ou sofisticados para ser efetiva. Ideal para estudantes e educadores que desejam trazer a teoria para a prática.

MENEZES, V.; RIBEIRO, A.; TECHIO, J.; REVILIAU, S.  Movimento Retilíneo Uniformemente Acelerado: Uma proposta de experimento de baixo custo. Revista Brasileira de Iniciação Científica. Itapetininga, v. 4, n. 2, 2017.

Queda livre e lançamento vertical

Quando falamos em queda livre e lançamento vertical, estamos abordando dois dos tópicos mais intrigantes e essenciais da física. O Capítulo 2.5 do livro Fundamentos da Física: Mecânica, escrito por Halliday, Resnick e Walker, fornece uma abordagem aprofundada sobre o Movimento Retilíneo, que é intrinsecamente relacionado à queda livre e ao lançamento vertical. Esse livro, não apenas oferece uma exposição teórica sólida, mas também apresenta ferramentas de interação que enriquecem o processo de aprendizagem e facilitam a compreensão dos conceitos de movimento.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

Referências Bibliográficas

BEER, F. P.; JOHNSTON JR., E. R.; CORNWELL, P. J. Mecânica vetorial para engenheiros: Dinâmica. 9. ed. Porto Alegre: AMGH, 2012.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

HIBBELER, R. C. Dinâmica: mecânica para engenharia. 14. ed. São Paulo: Pearson, 2017.

MENEZES, V.; RIBEIRO, A.; TECHIO, J.; REVILIAU, S. Movimento Retilíneo Uniformemente Acelerado: Uma proposta de experimento de baixo custo. Revista Brasileira de Iniciação Científica. Itapetininga, v. 4, n. 2, 2017.

MERIAM, J. L.; KRAIGE, L. G.; BOLTON, J. N. Mecânica para engenharia: Dinâmica. 9. ed. Rio de Janeiro: LTC, 2022.

Movimento em duas e três dimensões

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? 
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Partida

Olá, estudante! Estamos prestes a mergulhar em uma das partes mais intrigantes da física: o estudo de movimentos que ocorrem em duas e três dimensões. O que pode parecer complexo à primeira vista se tornará mais claro à medida que avançamos.

Aqui, abordaremos conceitos essenciais da física que se relacionam com movimentos em duas e três dimensões. Dentre eles, destacam-se a posição, velocidade e aceleração, além da análise aprofundada do lançamento de projéteis, compreendendo sua trajetória, altura máxima e alcance. Para fechar, nos debruçaremos sobre o movimento circular uniforme, distinguindo entre grandezas angulares e lineares. Esses são pilares fundamentais da mecânica e têm vasta aplicação, desde a simples observação de um objeto sendo arremessado até o design de máquinas e veículos.

Para isso, imagine que em uma cidade costeira, uma empresa de turismo marítimo decidiu inovar e criar um evento anual chamado "Festival de Lançamento de Foguetes Aquáticos". A ideia é construir pequenos foguetes que, ao serem lançados da superfície da água, façam um voo parabólico e, ao atingirem a altura máxima, liberem sementes biodegradáveis que se transformam em flores flutuantes, embelezando a superfície do mar.

Para o primeiro protótipo, a equipe técnica decidiu que o foguete será lançado com uma velocidade inicial de 20 m/s, fazendo um ângulo de 60^∘ com relação à horizontal. O objetivo multidisciplinar envolve a física para calcular a trajetória e o alcance do foguete, a biologia para escolher as melhores sementes que se transformarão em flores flutuantes e a engenharia para projetar o mecanismo de liberação das sementes.

Com base nos conceitos desta aula, você conseguirá prever a altura máxima que o foguete alcançará? Qual será a distância horizontal desde o ponto de lançamento até o ponto onde as sementes serão liberadas?

Vamos descobrir!

Vamos Começar!

Olá, estudante! Na física, o ponto material é uma simplificação idealizada que nos permite analisar movimentos sem nos preocuparmos com dimensões ou formas. No plano bidimensional (2D), esses movimentos se desenrolam em trajetórias lineares e circulares, enquanto no ambiente tridimensional (3D), eles exploram a vastidão do espaço em todas as direções. Entender esses conceitos básicos é crucial para a análise de sistemas mais complexos. Está pronto para aprender estes conceitos?

Movimento em duas e três dimensões

O movimento de uma partícula em um plano, frequentemente referido como movimento plano ou bidimensional, ocorre ao longo de duas dimensões – usualmente denominadas x (horizontal) e y (vertical), como pode ser visto na Figura 1. Esse tipo de movimento é frequentemente estudado em física para entender trajetórias que não são apenas em linha reta. Vamos explorar algumas características e conceitos principais relacionados ao movimento plano:

• Posição no plano: cada partícula tem seu "endereço" (x, y). É como um GPS em duas dimensões!
• Deslocamento: é o quão longe ela viajou do ponto inicial ao final. Imagina uma linha entre dois pontos? É isso!
• Velocidade: mostra o ritmo da viagem. Temos a direção (para onde) e a rapidez (quão rápido).
• Aceleração: se o ritmo muda, temos aceleração! Pode ser em x, y ou ambos.
• Trajetória: é a rota da jornada. Pode ser reta, curva, circular. É a pista que ela segue!

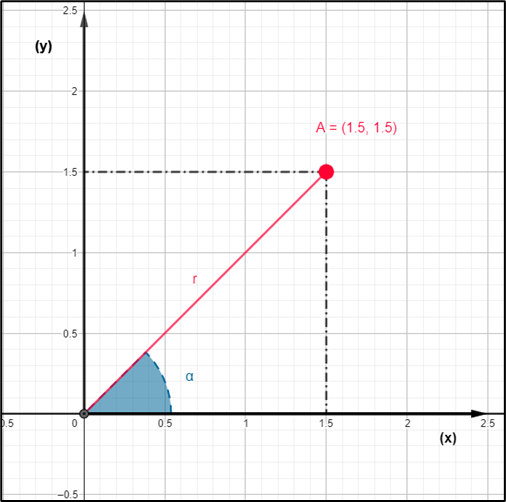
Agora, imagine isso em três dimensões! Elevamos tudo ao espaço. O movimento de uma partícula no espaço é um conceito fascinante que aborda a trajetória de um ponto material em três dimensões. Para entender completamente esse movimento, é importante explorar alguns conceitos e princípios fundamentais:

• Posição no espaço: aqui, adicionamos mais uma dimensão, o “z”. Então temos um endereço (x, y, z).
• Deslocamento: novamente, é a distância da viagem. Mas imagine em 3D, pode ser qualquer direção!
• Velocidade: mesma ideia, mas agora, pode ir pra cima, pra baixo, pros lados. Uma dança espacial!
• Aceleração: em 3D, temos ainda mais possibilidades de mudanças no ritmo.
• Trajetória: as rotas aqui podem ser retas, curvas, espirais. Como se fosse um drone voando em todas as direções.

Quando estudamos o movimento de uma partícula no espaço, muitas vezes encontramos sistemas de referência onde as leis da física são mais simples de serem aplicadas. Por exemplo, podemos escolher um sistema onde uma das coordenadas (digamos, z) é vertical e as outras duas (x e y) são horizontais, como pode ser visto na Figura 2.

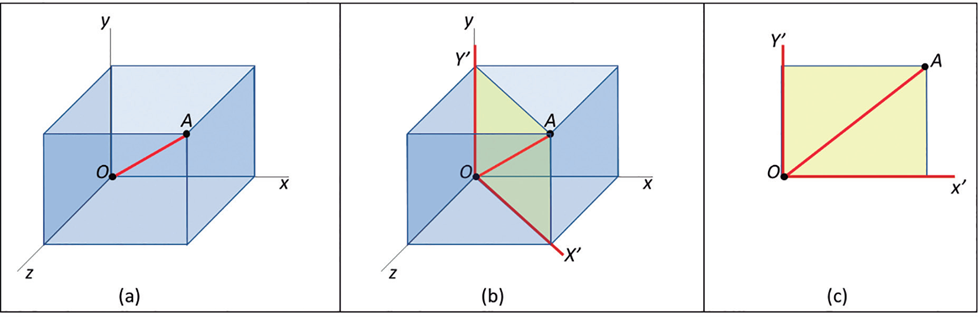
Observando a Figura 2, podemos ver que um movimento que começa parecendo 3D pode ser mostrado de forma mais simples, em 2D. Imagina traçar uma linha retinha da origem O até o ponto A; isso deixa tudo ainda mais fácil de entender!

Quando falamos de movimentos em 2D e 3D, é super prático usar vetores para mostrar coisas como posição, velocidade e aceleração. Usando vetores, fica mais fácil de entender tanto o "quanto" quanto o "para onde" de cada movimento. Então, ao invés de ficar só nas palavras, os vetores ajudam a entender melhor o que está acontecendo. Como a posição, velocidade e a aceleração são grandezas vetoriais, podemos decompô-las para ver como elas agem em cada pedacinho do nosso espaço ou plano. Assim, fica mais fácil entender e trabalhar com elas.

Assim, as equações do movimento para um plano são:

Eixo x:

$v_x=v_{0}x+a_{x}t$      (1)

$s_x=s_{0}x+v_{x}t$      (2)

$s_x=s_{0}x+v_{0}xt+1/2a_x{t}^2$      (3)

${v_x}^2=v_0{x}^2+2.a_x.\Delta s_x$      (4)

Eixo y:

$v_y=v_{0}y+a_{y}t$      (5)

$s_y=s_{0}y+v_{y}t$      (6)

$s_y=s_{0}y+v_{0}yt+1/2a_y{t}^2$      (7)

${v_y}^2=v_0{y}^2+2.a_y.\Delta s_y$      (8)

E para trabalharmos no espaço? Basta fazermos o mesmo processo e introduzirmos a coordenada z.

Exemplos clássicos do movimento plano incluem o lançamento de projéteis, denominado de movimento oblíquo (onde a partícula segue uma trajetória parabólica sob a influência da gravidade) e o movimento circular (onde a partícula se move ao longo de um círculo ou arco). Vamos compreender um pouco mais sobre eles?

Movimento oblíquo

Até agora, trabalhamos com velocidade e aceleração sendo vetoriais, até o momento foi possível estudá-las diferenciando os sentidos com sinais positivos e negativos, pois o movimento ocorria apenas em uma direção ou dimensão. Mas agora temos um desafio mais legal: o movimento oblíquo! Ele não é só para a frente ou para trás, ele vai para lados diferentes ao mesmo tempo, ou seja, o movimento acontece em ambos os eixos simultaneamente. Parece complicado? Não se preocupe, para isso, considere a Figura 3, que representa um referencial x, y utilizado para analisar um corpo que foi lançado obliquamente com velocidade inicial $\left(v{⃗}_0\right)$, formando um ângulo $\left(\theta \right)$ com a direção (x).

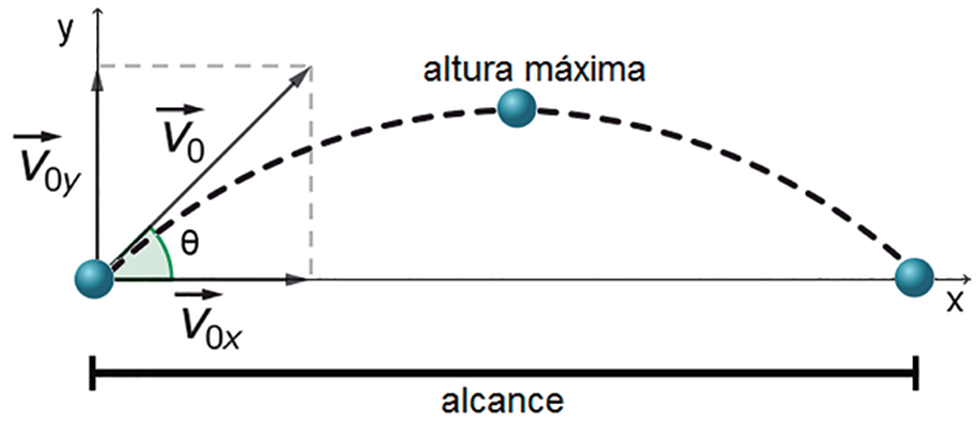
Na Figura 3, para encontrarmos as componentes de cada uma dessas velocidades é necessário realizar a decomposição vetorial por trigonometria.

$v_{o}x=v_0\cdot cos\left(\theta \right)$      (9)

$v_{o}y=v_0\cdot sen\left(\theta \right)$      (10)

Com essa decomposição, podemos analisar o movimento na direção x e na direção y, individualmente. Assim, olhamos para o movimento para a frente (direção x) e para cima (direção y) como se fossem movimentos separados e isso só é possível pelo princípio da Independência dos Movimentos, proposto por Galileu, que declara que, em um sistema onde não há resistências (como o atrito ou a resistência do ar), o movimento de um corpo em uma direção é independente de seu movimento em outra direção.

Então, se desconsiderarmos a resistência do ar, o movimento para cima é como se estivéssemos jogando algo para o alto. Primeiro, ele vai desacelerando até parar e depois acelera de volta para terra. E nessa análise, nossa referência vertical (y) considera que jogar algo para cima é positivo e a aceleração é a gravidade, ou seja, a = - g. Então, o movimento oblíquo acontece em dois movimentos:

1. Movimento horizontal (na direção x): esse movimento é uniforme, ou seja, o corpo se move a uma velocidade constante na direção horizontal, desde que desconsideremos a resistência do ar.
2. Movimento vertical (na direção y): esse movimento é uniformemente acelerado devido à aceleração da gravidade. Assim, o corpo lançado sobe desacelerando até atingir sua altura máxima e, depois, começa a cair acelerando devido à gravidade.

As equações do movimento oblíquo são as mesmas utilizadas para o movimento em um plano, ou seja, as Equações de (1) a (8). Mas, antes de usarmos elas, é importante fazer uma análise do movimento, tudo bem? Para analisarmos o movimento, vamos imaginar que jogamos uma bola num ângulo meio inclinado e ver ela voar, subindo e depois caindo. Esse é o nosso movimento oblíquo! Agora, para entender melhor, temos algumas regrinhas e ideias para te mostrar:

• Subindo e descendo: quando jogamos a bola para cima, ela começa a desacelerar porque a gravidade a puxa pra baixo, certo? Então, nessa subida, a gravidade atua como uma "aceleração negativa". Mas, quando ela começa a cair de volta, é como se a gravidade desse um empurrãozinho, tornando-se uma "aceleração positiva".
• Movendo-se para frente: enquanto nossa bola está no ar, ela também está se movendo para frente, certo? E essa parte é bem tranquila, porque ela vai se mover numa velocidade constante. Não tem nenhuma força extra a empurrando ou puxando nessa direção.
• Altura máxima: é o ponto mais alto que a bola alcança antes de começar a cair de novo. É aqui que ela dá uma pausa e sua velocidade vertical é zero.
• Alcance máximo: pensa em quão longe a bola vai horizontalmente enquanto está no ar. O mais longe que ela pode ir é quando a lançamos em um ângulo de 45° (se não considerarmos coisas como resistência do ar).
• Tempo de subida: é o tempo que a bola leva para chegar naquela altura máxima. E podemos determinar ela por meio da Equação (11):

$\left(t_s\right):0=[v_0\cdot sen(\theta \left)\right]-g.t_s$

$t_s=\frac{v_0\cdot sen\left(\theta \right)}{g}$      (11)

• Tempo total: aqui é legal: a bola leva o mesmo tempo para subir e para descer. Então, o tempo total de voo dela é só o dobro do tempo de subida!

Com o movimento oblíquo bem compreendido, vamos embarcar em outra jornada fascinante: o movimento circular! Prepare-se para explorar as curvas e voltas que essa dinâmica nos apresenta.

Siga em Frente...

Movimento Circular Uniforme (MCU)

O Movimento Circular Uniforme (MCU) é uma forma interessante de movimento que você já deve ter observado no dia a dia. Pense na hélice de um ventilador girando: ela completa voltas a uma velocidade constante. Esse é o MCU em ação! Mesmo com velocidade constante, a direção dessa velocidade está sempre mudando.

A aceleração, em física, está relacionada a mudanças na velocidade. No MCU, embora a magnitude da velocidade permaneça constante, sua direção está sempre mudando. Essa mudança direcional é causada por algo chamado aceleração centrípeta, que sempre direciona para o centro do movimento circular. Na Figura 4, você pode ver como essa aceleração atua, sempre apontando para o centro e a velocidade sempre atuando tangencialmente a trajetória.

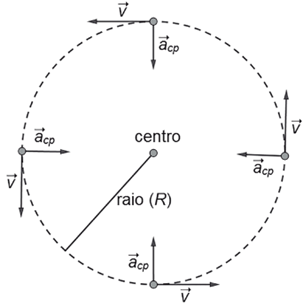
Para entender melhor, há uma equação que relaciona a aceleração centrípeta à velocidade e ao raio da trajetória:

$a{⃗}_{cp}=\frac{V^2}{R}$      (12)

Sua unidade de medida no SI também é m/s².

Dentro do MCU também temos conceitos como período e frequência. O período é o tempo necessário para o objeto completar uma revolução completa. Já a frequência indica quantas revoluções o objeto faz em um segundo, e essa medida é chamada de "hertz" (Hz).

Imagine um motor que gira bem rápido: quatro rotações a cada segundo! Isso quer dizer que sua frequência é 4 Hz. E, se você parar para pensar, cada volta desse motor demora só um quarto de segundo (0,25 s) para completar. Legal, né? E sabe o que descobrimos aqui? Se você pegar o número 1 e dividir pela frequência, você consegue o período. Então, 1 dividido por 4 Hz é igual a 0,25 s. Assim, neste exemplo, podemos verificar que o período é $T=\frac{1}{f}$ e a frequência é $f=\frac{1}{T}$.

O movimento que esse motor faz, girando em círculo, é o que chamamos de Movimento Circular Uniforme (MCU). Como ele gira em um círculo, podemos falar um pouco sobre os ângulos: uma volta completa do motor é igual a 360°, ou se preferir, é igual a 2π radianos. Se um objeto (ponto material) está fazendo esse MCU, ele tem uma "velocidade angular" (simbolizada por ω). Essa velocidade nos diz o quanto o ângulo muda em relação ao tempo. Portanto, para uma volta completa:

$\omega =\frac{\Delta \theta }{\Delta t}=\frac{2\pi }{T}=2\pi f$      (13)

Agora, sobre a velocidade real do objeto em movimento: ele percorre o tamanho inteiro do círculo (que chamamos de circunferência) a cada volta. A fórmula do tamanho da circunferência é $\mathit{C}\mathbf{=}\mathbf{2}\mathit{\pi }\mathit{R}$, onde R é o raio do círculo. Se você pegar essa circunferência e dividir pelo período (ou multiplicar pelo raio e pela frequência), você consegue a velocidade. Um detalhe legal para terminar: a velocidade do objeto também pode ser encontrada multiplicando a velocidade angular pelo raio. Ou seja, $\mathit{V}=\mathit{R}.\mathit{\omega }$.

Caro estudante, nesta aula navegamos pela complexidade e beleza dos movimentos, abordando desde as sutilezas das duas e três dimensões até o intrigante mundo dos projéteis. Discutimos suas trajetórias, pontos máximos e distâncias alcançadas. Além disso, mergulhamos profundamente no movimento circular uniforme, desvendando as relações entre grandezas angulares e lineares. Esta jornada nos permite uma maior apreciação da física e de como ela molda e explica os fenômenos ao nosso redor.

Vamos Exercitar?

Retomando a nossa problemática do “Festival de Lançamento de Foguetes Aquáticos”, sabemos que para o primeiro protótipo, a equipe técnica decidiu que o foguete será lançado com uma velocidade inicial de 20 m/s, fazendo um ângulo de 60° com relação à horizontal e nós devemos calcular a trajetória e alcance do foguete.

Vamos iniciar determinando as componentes verticais ${ (v}_{oy})$ e horizontais $\left(v_{ox}\right)$ da velocidade:

$v_{ox}=v_0\cdot cos\left(\theta \right)$

$v_{ox}=20.cos\left({60}^0\right)=20. \mathrm{0,5}=10\frac{m}{s}$

$v_{oy}=v_0\cdot \mathrm{sen}\left(\theta \right)$

$v_{oy}=20.sen\left({60}^0\right)=20. \frac{\sqrt{3}}{2}\approx \mathrm{17,32}\frac{m}{s}$

Agora, aplicando a equação de Torricelli para esse movimento, é possível determinar a altura máxima e o tempo para atingi-la:

$h_{max}=\frac{v_{O_y}^2}{2g}, sendo g=\mathrm{9,81}\frac{m}{s^2}$

$h_{max}=\frac{{\left(\mathrm{17,32}\right)}^2}{\mathrm{2.9,81}}\approx \mathrm{15,35} m$

$v_{0y}=g.t$

$t= \frac{v_{0y}}{g}= \frac{\mathrm{17,32} }{\mathrm{9,81}}=\mathrm{1,77} s$

O foguete leva 1,77 segundos para atingir sua altura máxima, como mencionado anteriormente. Então, o tempo total que o foguete fica no ar é de t_max = 3,54 segundos. Como a velocidade horizontal do foguete (que não muda, já que a resistência do ar não está sendo considerada) é de 10 m/s, então o alcance horizontal (S) é a velocidade horizontal multiplicada pelo tempo total de voo:

$S=v_{0x}.t=10. \left(\mathrm{3,54}\right)=\mathrm{35,4} m$

Finalizamos os cálculos para o Festival de Lançamento de Foguetes Aquáticos. Esperamos que os conceitos discutidos tenham sido claros e que você tenha sido capaz de incorporá-los eficazmente na resolução das questões proposta. Não se esqueça: a física está presente em muitos aspectos do nosso cotidiano e, quanto mais a entendemos, mais podemos nos maravilhar com os fenômenos ao nosso redor. Continue estudando e buscando sempre se aperfeiçoar. Até a próxima!

Saiba Mais

Movimento em duas e três dimensões

Mergulhe no mundo da física com este guia abrangente. No Capítulo 3 do livro Física para Cientistas e Engenheiros, de Paul A. Tipler e Gene Mosca, os autores exploram conceitos fundamentais relacionados à cinemática vetorial, abordando posição, velocidade e aceleração em duas e três dimensões. Essa leitura é essencial para quem quer fortalecer seu entendimento sobre o tema e ver aplicações práticas desses conceitos.

Para um entendimento aprofundado e uma visão detalhada sobre o assunto, esse capítulo é altamente recomendado. Ele proporciona uma explicação clara e objetiva, com exemplos e exercícios que ajudam na compreensão e fixação do conteúdo. Aproveite a leitura! O livro está disponível na Biblioteca Virtual.

TIPLER, P. A.; MOSCA, G. Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica. v.1. Grupo GEN, 2009.

Movimento oblíquo

Adentre os debates intrigantes do passado científico e descubra as controvérsias por trás da trajetória parabólica dos projéteis! O artigo, escrito por Júlio Celso Ribeiro de Vasconcelos da Universidade Estadual de Feira de Santana - UEFS, aborda polêmicas envolvendo essa trajetória e sua atribuição a Galileo Galilei. Com histórias de alegadas falsificações de documentos e interpretações variadas de manuscritos redescobertos, este artigo oferece uma visão profunda sobre a evolução do nosso entendimento da física dos projéteis. 

Artigo acadêmico de acesso aberto: Galileo e a Forma Parabólica da Trajetória dos Projéteis.

VASCONCELOS, J. C. R. de. Galileo e a Forma Parabólica da Trajetória dos Projéteis. Revista Ideação. Dossiê Especial NEF 2020.

Mergulhe nas polêmicas e nos debates que moldaram nossa compreensão sobre as trajetórias dos projéteis e desvende os mistérios por trás das descobertas de Galileu.

Movimento Circular Uniforme

Se você quer entender melhor o conceito por trás dos movimentos circulares, o Capítulo 10 do livro Fundamentos de Física - Mecânica é o seu guia ideal. Nesta obra consagrada, os autores David Halliday, Robert Resnick e Jearl Walker desvendam os mistérios da mecânica de forma clara e didática. É uma leitura essencial para quem busca aprofundar seus conhecimentos em física. O livro está disponível na Biblioteca Virtual.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

Referências Bibliográficas

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

HIBBELER, R. C. Dinâmica: mecânica para engenharia. 14. ed. São Paulo: Pearson, 2017.

JUDICE, G. H. Mecânica geral. Londrina: Editora e Distribuidora Educacional S.A., 2018. 224 p.

MERIAM, J. L.; KRAIGE, L. G.; BOLTON, J. N. Mecânica para engenharia: dinâmica. 9. ed. Rio de Janeiro: LTC, 2022.

NEGRÃO, L. C. Física geral. Londrina: Editora e Distribuidora Educacional S.A., 2018. 240 p.

Videoaula de Encerramento

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la?
Clique aqui para acessar os slides da sua videoaula.
Bons estudos!

Ponto de Chegada

Olá, estudante! Para desenvolver a competência desta Unidade, que é "descrever e compreender os conceitos e leis da mecânica clássica", começamos por compreender as bases que norteiam a física: as grandezas e, para aplicar os conceitos relacionados à cinemática, é imprescindível analisar movimentos em uma e duas dimensões de forma precisa e adequada.

Abordamos inicialmente as grandezas físicas, dando ênfase às unidades, à notação científica, aos prefixos e ao sistema internacional (SI). Esse conhecimento nos permite compreender e padronizar as medidas que usamos para descrever o mundo ao nosso redor.

Em seguida, mergulhamos nas grandezas vetoriais e escalares, destacando suas diferenças essenciais. As grandezas escalares têm magnitude, mas não direção, como a temperatura. Já as vetoriais possuem tanto magnitude quanto direção, como a velocidade. Aprofundamo-nos ainda mais na representação gráfica de vetores, detalhando como determinar módulo, direção e sentido. E, claro, não deixamos de lado as operações fundamentais com vetores, como adição, subtração e a crucial decomposição de vetores.

Continuando nossa jornada pelo universo da mecânica clássica, chegamos a pontos cruciais para o entendimento aprofundado da cinemática: o conceito de referencial inercial e a ideia de movimento relativo. Saber escolher e entender um referencial é fundamental, pois todo movimento é descrito em relação a algo, e essa escolha influencia como percebemos e medimos esse movimento. Em um referencial inercial, as leis da física são simples e diretas, enquanto em outros referenciais, elas podem parecer complicadas.

Com esse referencial em mente, voltamos nossa atenção para a descrição do movimento. Começamos com os conceitos básicos de posição e deslocamento, que nos dão uma ideia de onde um objeto está e quão longe ele se moveu. A velocidade média, por sua vez, nos informa o quão rápido esse deslocamento ocorre em um intervalo de tempo, enquanto a aceleração média nos mostra como essa velocidade muda nesse período.

Mas e se quisermos uma visão mais precisa, um retrato de um instante específico? É aí que entram a velocidade instantânea e a aceleração instantânea. Em vez de olhar para todo um intervalo de tempo, nos concentramos em um ponto específico, permitindo-nos entender as nuances do movimento em qualquer momento.

Ao dominar esses tópicos, você não apenas descreve o movimento de forma ampla, mas também entende suas variações sutis e instantâneas. Isso amplia sua capacidade de aplicar os conceitos de cinemática em situações do dia a dia e em problemas complexos.

Avançando em nossa exploração, chegamos a padrões de movimento mais específicos que ocorrem frequentemente em nosso mundo. Primeiramente, temos o Movimento Retilíneo Uniforme (MRU), onde um objeto se desloca em linha reta com velocidade constante. Nesse tipo de movimento, não há aceleração; a velocidade não muda, e o objeto se move a uma taxa constante. É como um carro que mantém uma velocidade constante em uma estrada retilínea. Já no Movimento Retilíneo Uniformemente Variado (MRUV), há uma aceleração constante atuando sobre o objeto. Isso significa que sua velocidade muda uniformemente com o tempo. Um exemplo típico seria um carro acelerando ou desacelerando em linha reta.

Mergulhando mais fundo, chegamos à queda livre, uma situação específica de MRUV onde a única força atuando sobre um objeto é a gravidade. Aqui, objetos de diferentes massas caem com a mesma aceleração (desprezando o atrito do ar). É um fenômeno que Galileu estudou em detalhes e que desafia nossa intuição comum.

Por fim, temos o lançamento vertical. Quando lançamos um objeto verticalmente para cima, ele sobe até que sua velocidade se torne zero e depois começa a cair de volta, sendo influenciado apenas pela gravidade. A análise desse movimento é fascinante e revela muitos dos princípios fundamentais da mecânica.

Também foi possível compreender a posição, velocidade e aceleração em duas e três dimensões. No mundo ao nosso redor, os objetos não se limitam a mover-se em um único plano. Eles se deslocam em várias direções, e entender como essas grandezas variam e interagem é crucial para desvendar os mistérios da cinemática.

Mas o que ocorre quando lançamos um objeto no ar, como uma bola ou uma pedra? A trajetória que ele desenha no céu, atingindo uma altura máxima e depois retornando ao solo, exemplifica o lançamento de projéteis. Ao estudar esses movimentos, você aprende a prever e calcular aspectos essenciais, como a distância máxima que um projétil viaja e a altura que alcança.

Por fim, exploramos o fascinante mundo do movimento circular uniforme. Imagine um carrossel girando ou a Terra orbitando o Sol; esses movimentos circulares capturam nossa atenção. Aqui, diferenciamos entre grandezas angulares, que se referem ao giro, e grandezas lineares, relacionadas ao caminho que percorremos ao longo do círculo.

Ao dominar esses tópicos, você está se capacitando para aplicar os conceitos da cinemática, analisando movimentos de partículas em uma e duas dimensões com confiança e precisão. Portanto, é o momento de mergulhar nesses conceitos, pois sua habilidade de analisar e descrever os movimentos depende diretamente deles.

É Hora de Praticar!

Uma startup inovadora está trabalhando em um projeto para otimizar o transporte de produtos químicos sensíveis ao clima, usando sensores avançados. Esses sensores detectam movimentos e alterações em duas e três dimensões durante o transporte, assegurando que os produtos se mantenham estáveis e seguros. Para garantir a eficácia desse projeto, a equipe precisa aplicar conceitos de cinemática, desde o deslocamento até o monitoramento da velocidade e aceleração dos veículos transportadores. Como os conceitos de cinemática podem ser aplicados para assegurar a estabilidade dos produtos durante o transporte? Como os sensores podem interpretar movimentos em duas e três dimensões para otimizar a rota de transporte? Que ajustes poderiam ser feitos no caso de movimentos imprevistos ou acelerações repentinas?

Reflita

• Como o sistema internacional (SI) padroniza e facilita o entendimento e a comunicação em estudos científicos em todo o mundo?
• Como os esportes, como o basquete ou o futebol ilustram a importância de entender o movimento em múltiplas dimensões?
• Como a habilidade de analisar movimentos em uma e duas dimensões pode ser aplicada em seu campo profissional?

Resolução do estudo de caso

Para desenvolver a competência de descrever e compreender os conceitos e as leis da mecânica clássica, é crucial aplicar os fundamentos da cinemática. Nesse cenário proposto, vemos a relevância da cinemática no mundo real, especialmente quando se trata de garantir a segurança e estabilidade de produtos sensíveis durante o transporte.

Os sensores, ao detectarem movimentos em duas e três dimensões, podem fornecer dados em tempo real sobre o deslocamento, a velocidade e a aceleração do veículo. Ao monitorar esses parâmetros, o sistema pode ajustar a rota ou a velocidade do veículo, se necessário. Por exemplo, se um veículo acelerar rapidamente ou fazer uma curva acentuada, os sensores podem detectar esse movimento e o sistema pode ajustar o veículo para manter os produtos estáveis.

Não existe uma única solução para esse desafio. Uma abordagem pode envolver o uso de algoritmos avançados para interpretar os dados dos sensores e fazer ajustes em tempo real. No entanto, é essencial que os estudantes reflitam sobre outras possíveis soluções e abordagens, sempre tendo em mente a aplicação dos conceitos de cinemática.

Dê o play!

Assimile

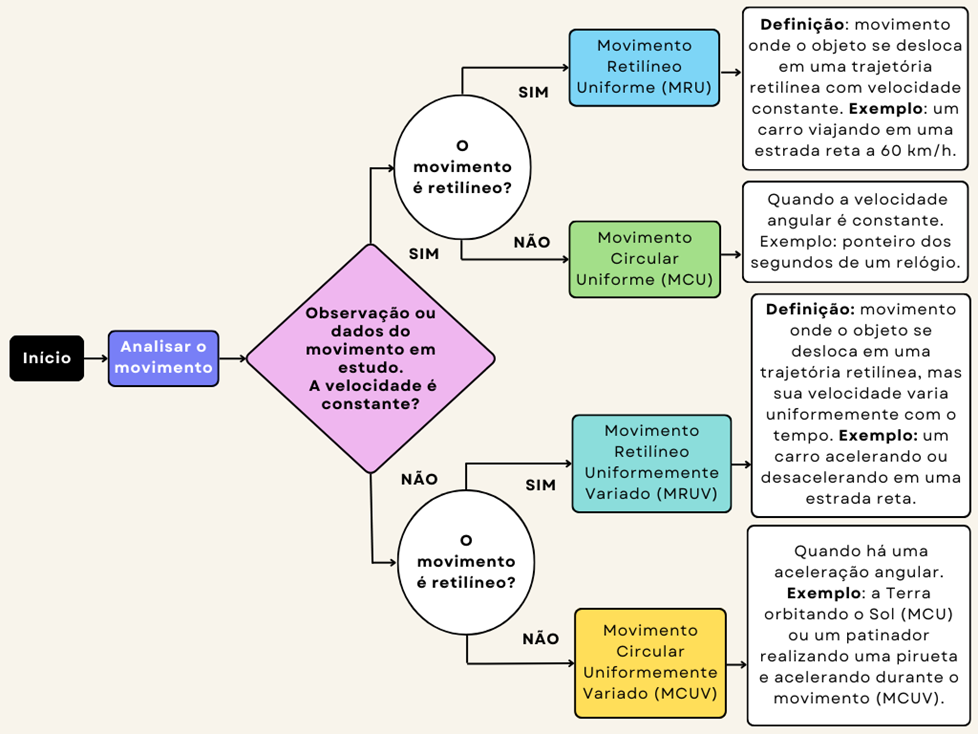
Referências

BEER, F. P.; JOHNSTON JR., E. R.; CORNWELL, P. J. Mecânica vetorial para engenheiros: dinâmica. 9. ed. Porto Alegre: AMGH, 2012.

CUTNELL, J. D.; JOHNSON, K. W. Física. 9. ed. Rio de Janeiro: LTC, 2016. v. 1.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: mecânica. 12. ed. Rio de Janeiro: LTC, 2023.

HIBBELER, R. C. Dinâmica: mecânica para engenharia. 14. ed. São Paulo: Pearson, 2017.

MERIAM, J. L.; KRAIGE, L. G.; BOLTON, J. N. Mecânica para engenharia: dinâmica. 9. ed. Rio de Janeiro: LTC, 2022.