Fundamentos Gerais Sobre Funções

Funções afim e quadrática

Olá, estudante! Nesta videoaula você conhecerá os conceitos básicos envolvendo as funções, com destaque para as características das funções afim e quadrática, que são parte da classe das funções polinomiais.

Este conteúdo é importante para a sua prática profissional, pois o conceito de função pode ser empregado quando desejamos descrever relações existentes entre variáveis, as quais podem estar presentes em múltiplos contextos.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Estudante, desejamos a você boas-vindas! Vamos iniciar nossos estudos a respeito do conceito de função, o qual está presente em diversas situações, especificamente quando podemos interpretá-las como um tipo de relação entre duas variáveis, considerando os mais diversos contextos nos quais elas estão inseridas. Entre os diversos tipos de funções vamos destacar as funções afim e quadrática, ambas do tipo polinomiais.

Para favorecer esse estudo, vamos analisar a seguinte problemática. Um grupo de empresários, proprietários de uma empresa de transporte por aplicativo, está buscando uma parceria com empresas locadoras de veículos para seus associados. Em suas buscas, eles localizaram duas possíveis parceiras: a AluCar e a LocMotors. Essas locadoras cobram suas tarifas da seguinte forma:

• A tarifa mensal cobrada para o aluguel de um automóvel padrão pela Alucar corresponde a um valor fixo de R$ 320,00 acrescido de R$ 0,30 por quilômetro rodado.
• A tarifa mensal cobrada para o aluguel de um automóvel padrão pela LocMotors é composta de um valor fixo de R$ 140,00 acrescido de R$ 0,45 por quilômetro rodado.

Em quais condições compensa escolher uma ou outra empresa para a locação de veículos?

Assim, para a resolução da situação apresentada, prossiga em seus estudos, tomando como referência as propriedades das funções e selecionando a categoria de função mais adequada para a solução desse problema. 

Vamos Começar!

Em nosso cotidiano nos deparamos com várias situações nas quais devemos relacionar variáveis entre si, por exemplo, quando comparamos as quantidades de combustível consumidas por um automóvel com as distâncias percorridas. Esse tipo de situação pode ser estudada por meio do conceito de função, o qual permite associar duas variáveis entre si. Vejamos a seguir como podemos definir uma função e quais as possíveis representações.

Introdução às funções

Uma função $f$ corresponde a uma regra que associa cada elemento $x$, pertencente a um conjunto $D$, a um único elemento $f\left(x\right)$, pertencente a um conjunto $E$. Nesse caso, podemos empregar a representação $F:D\to E$. Para que seja definida uma função, cada elemento do conjunto $D$ deve estar relacionado somente a um elemento de $E$. Uma representação possível para uma função é o diagrama de flechas, conforme Figura 1.

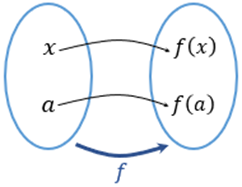
Figura 1 | Diagrama de flechas para uma função $f$

No diagrama de flechas da Figura 1 apresentamos os dois conjuntos, $D$ e $E$ empregados na construção da função, e as relações existentes entre seus elementos por meio de flechas.

No estudo de uma função $f:D\to E$, o conjunto $D$ é chamado de domínio de função, no qual são indicados os possíveis valores assumidos pela variável independente, a qual pode ser representada por $x$. O conjunto $E$, por sua vez, consiste no contradomínio da função, no qual é estudada a variável dependente. Além disso, os possíveis valores de $f\left(x\right)$, obtidos ao variar $x$ por todo o domínio, pertencem a um subconjunto de $E$ chamado de imagem de $f$. As funções, conforme a definição apresentada, podem ser chamadas também de funções de uma variável, visto que temos a presença de uma única variável independente.

Além do diagrama de flechas, podemos representar as funções a partir de gráficos, os quais permitem analisar o comportamento da função, observando como se relacionam as variáveis dependente e independente. O gráfico de uma função $f:D\to E$ corresponde a um conjunto de pares ordenados $\left(x,y\right)$ em que $y=f\left(x\right)$, com $x$ pertencente ao domínio  da função. Esse conjunto pode ser descrito como $G=\left\{\left(x,f\left(x\right)\right);x\in D\right\}$. Desse modo, partindo do plano cartesiano, a construção de um gráfico envolve a identificação dos pares ordenados envolvendo os valores do domínio com suas imagens correspondentes. Na Figura 2 podemos observar um exemplo de gráfico, associado a uma função f, observando o domínio e a imagem correspondentes.

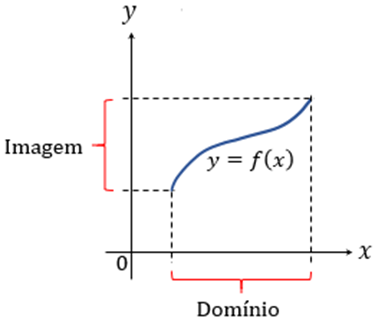
Figura 2 | Gráfico da função $f:D\to E$

Nas representações gráficas, como é o caso da Figura 2, os pares ordenados sempre são identificados de modo que os elementos do domínio sejam representados a partir do eixo das abscissas (horizontal), denominado eixo $x$, e a imagem seja descrita a partir do eixo das ordenadas (vertical), descrito como eixo $y$. Também temos a possibilidade de estudar funções definidas a partir de uma tabela de valores, ou ainda a partir de uma expressão matemática que a caracteriza. Um exemplo de função representada algebricamente consiste em:

$f:\mathrm{ℝ}\to \mathrm{ℝ}$

$x\mapsto x+1$

Nesse caso, para cada $x$, número real, sua imagem é tal que $f\left(x\right)=x+1$. A expressão $\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}+1$ como a regra ou a lei de formação da função, a qual deve ser apresentada em conjunto com domínio e contradomínio adequados. A representação gráfica para essa função é apresentada na Figura 3.

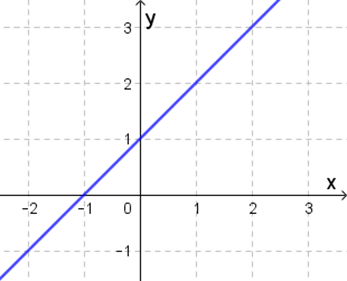
Figura 3 | Representação gráfica para $f$, com $f\left(x\right)=x+1$

Além disso, podemos construir uma tabela de valores associados à $f$, conforme a Tabela 1, de modo a estudar a função em certos pontos de seu domínio.

$x$	$f\left(x\right)$
-2	-1
-1	0
0	1
1	2
2	3

Tabela 1 | Valores correspondente à função $f$, com $f\left(x\right)=x+1$

Além dessas propriedades, de acordo com a lei de formação de uma função, podemos construir categorias específicas, das quais podemos destacar as funções polinomiais, exponenciais, logarítmicas, entre outras.

Uma função polinomial consiste em uma função $f:R\to R$ cuja lei de formação é dada por $f\left(x\right)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+\dots +a_{n-1}{x}^{n-1}+a_n{x}^n$, sendo $n$ um número inteiro não negativo e os números $a_0,a_1,a_2,\dots ,a_n$ são constantes denominadas coeficientes do polinômio. Desde que o coeficiente dominante $a_n$ seja diferente de zero, então o grau do polinômio é igual a $n$. No conjunto das funções polinomiais podemos destacar duas subcategorias importantes: o conjunto das funções polinomiais de grau 1, chamadas de funções afim, e as funções polinomiais de grau 2, denominadas funções quadráticas, as quais são apresentadas a seguir.

 

Siga em Frente...

Função afim

Uma função $f:\mathrm{ℝ}\to \mathrm{ℝ}$ cuja lei de formação é $f\left(x\right)=ax+b$, com $a$ e $b$ números reais, é denominada função polinomial de 1º grau ou função afim. A constante real $a$ é denominada coeficiente angular e $b$ é chamada de coeficiente linear. O gráfico que descreve uma função dessa classe é representado por uma reta no plano cartesiano, o que permite o emprego desse tipo de função na representação de fenômenos com característica linear, como é o caso do valor pago por uma quantidade específica de unidades de um mesmo produto, por exemplo, considerando a ausência de descontos. Por exemplo, a função $f:\mathrm{ℝ}\to \mathrm{ℝ}$ com $f\left(x\right)=2x-1$ é afim, cujo gráfico é ilustrado na Figura 4.

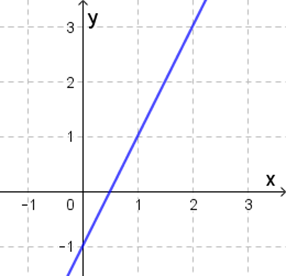
Figura 4 | Gráfico da função real $f$ com lei de formação $f\left(x\right)=2x-1$

No conjunto das funções afim, podemos ainda destacar os seguintes casos particulares:

• Função linear: apresenta lei de formação na forma $f\left(x\right)=ax$, com $a$ um número real.
• Função constante: apresenta lei de formação como $f\left(x\right)=b$, com $b$ um número real.

O gráfico de uma função linear pode ser identificado como uma reta que passa pela origem, isto é, que contém o par ordenado , enquanto o gráfico de uma função constante corresponde a uma reta paralela ao eixo x.

O estudo do crescimento e decrescimento de funções afim pode ser realizado com base no coeficiente angular associado, de modo que em uma função crescente o coeficiente angular é positivo $\left(a>0\right)$, e na função decrescente o coeficiente angular é negativo $\left(a<0\right)$.

Além disso, independentemente do crescimento ou decrescimento da função, um valor $x\in \mathrm{ℝ}$, no domínio de uma função afim, é chamado de raiz da função quando $f\left(x\right)=0$, o qual é caracterizado, graficamente, como a interseção do gráfico da função com o eixo $x$.

Além das funções afim, uma outra classe importante de funções polinomiais corresponde nas funções polinomiais de 2º grau ou funções quadráticas.

Função quadrática

Uma função $f:\mathrm{ℝ}\to \mathrm{ℝ}$ cuja lei de formação é $f\left(x\right)=a{x}^2+bx+c$, com $a$, $b$ e $c$ números reais e $a\ne 0$, é denominada função polinomial de 2º grau ou função quadrática. O gráfico que descreve uma função dessa classe é representado por uma parábola no plano cartesiano. Por exemplo, a função $f:\mathrm{ℝ}\to \mathrm{ℝ}$ com $f\left(x\right)=2x^2+x-1$ é uma função quadrática, cujo gráfico é ilustrado na Figura 5.

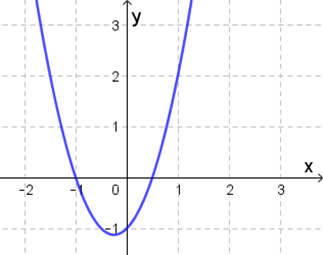
Figura 5 | Gráfico da função real $f$ com lei de formação $f\left(x\right)=2x^2+x-1$

O coeficiente $a$, do termo de grau 2, é responsável por indicar o comportamento da parábola em relação à sua concavidade. Quando $a>0$ a parábola que representa graficamente a função quadrática tem concavidade voltada para cima, enquanto $a<0$ indica que a parábola terá concavidade voltada para baixo.

Também podemos estudar as raízes associadas a funções quadráticas considerando, de modo análogo às funções afim, que $x\in \mathrm{ℝ}$ no domínio da função $f$ é uma raiz quando $f\left(x\right)=0$. Sendo assim, $x$ é uma raiz quando for solução da equação de 2º grau na forma $x^2+bx+c=0$. Para estudar os tipos de raízes que uma função quadrática pode apresentar podemos estudar o discriminante $\left(\mathrm{\Delta }=b^2-4\cdot a\cdot c\right)$. A partir do discriminante podemos inferir que a função quadrática apresentará:

• Duas raízes reais distintas quando o discriminante for positivo $\left(\mathrm{\Delta }>0\right)$.
• Duas raízes reais e iguais, ou uma raiz de multiplicidade 2, quando o discriminante for nulo $\left(\mathrm{\Delta }=0\right)$.
• Duas raízes complexas conjugadas quando o discriminante for negativo $\left(\mathrm{\Delta }<0\right)$.

As raízes podem ser obtidas a partir do estudo da equação de 2º grau associada, possibilitando o emprego da fórmula resolutiva para equações do 2º grau na forma $x=\frac{-b\pm \sqrt{\mathrm{\Delta }}}{2\cdot a}$. Combinando as análises em relação à raízes e concavidade, podemos identificar uma das seis possibilidades para o gráfico da função quadrática, conforme situações ilustradas na Figura 6.

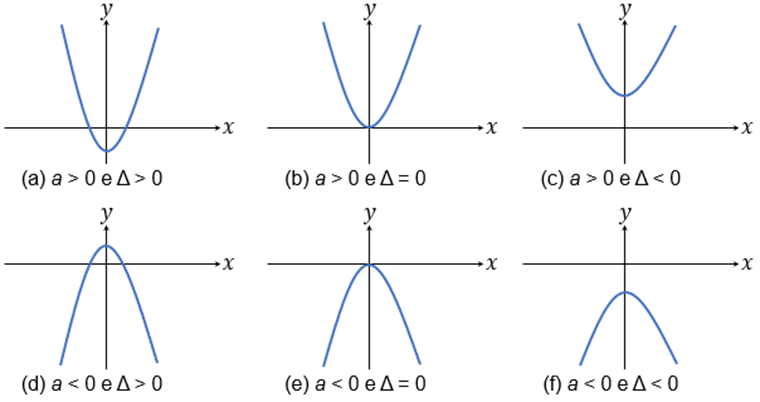
Figura 6 | Estudo do sinal e das raízes de uma função quadrática

Além das propriedades já estudadas, outro elemento que se faz presente no gráfico de uma função quadrática é o vértice, o qual consiste no ponto em que o gráfico altera entre os comportamentos de crescimento e decrescimento. O vértice corresponde a um ponto de coordenadas $\left(x_v,y_v\right)$ em que $x_v=-\frac{b}{2\cdot a}$ e $y=-\frac{\mathrm{\Delta }}{4\cdot a}$. Note que o vértice pode corresponder a um valor mínimo, quando a parábola tem concavidade voltada para cima, ou máximo, se a concavidade é voltada para baixo, dependendo da lei de formação e do domínio da função.

O conhecimento do conceito de função e suas propriedades é essencial quando desejamos interpretar fenômenos por meio dos recursos matemáticos, principalmente quando podemos identificar relações entre variáveis, sejam essas situações provenientes de contextos matemáticos ou de outras áreas do conhecimento. 

Vamos Exercitar?

Para solucionar o problema apresentado, envolvendo as locadoras de veículos, vamos descrevê-las por meio de uma função. Nesse caso, vamos utilizar a representação $q$ para a quantidade de quilômetros rodados mensalmente no estudo de cada empresa.

Considerando a empresa Alucar, o cálculo da tarifa $T_A$ pode ser feito por meio de uma função afim, cuja lei de formação é $T_A\left(q\right)=\mathrm{0,30}q+320$, sendo seu domínio dado por ${\mathrm{ℝ}}_{+}=\left\{x\in \mathbb{ }\mathrm{ℝ};x\ge 0\right\}$. Nesse sentido, temos a notação:

$T_A:{\mathrm{ℝ}}_{+}\to \mathrm{ℝ}$

$q\mapsto \mathrm{0,30}q+320$

Por outro lado, no caso da empresa LocMotors, a tarifa $T_L$ pode ser calculada por $T_L\left(q\right)=\mathrm{0,45}q+140$, com o mesmo domínio da anterior, e de tal modo que:

$T_L:{\mathrm{ℝ}}_{+}\to \mathrm{ℝ}$

$q\mapsto \mathrm{0,45}q+140$

Observe que ambas as funções são afim, ou polinomiais de 1º grau. Construindo as representações para elas em um mesmo plano cartesiano, podemos obter o gráfico conforme a Figura 7, em que o eixo das abscissas indica a quilometragem e o das ordenadas, o custo.

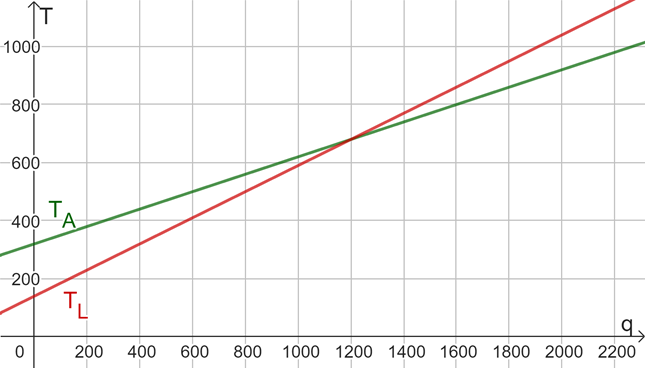
Figura 7 | Comparações entre os planos para locação de veículos

A partir do gráfico da Figura 7, podemos observar que há uma interseção em $q=1200$, ou seja, para 1200 km percorridos, o preço pago do aluguel é o mesmo, de modo que a LocMotors compensa para trajetos inferiores a 1200 km, e a Alucar, para trajetos superiores a 1200 km. Isso também pode ser avaliado igualando as leis de formação de ambas as funções (mesma tarifa), ou recorrendo a inequações, o que conclui a solução do problema. 

 

 

Saiba Mais

Um material bastante interessante para o estudo dos conceitos iniciais envolvendo as funções é o livro Pré-Cálculo de Sheldon Axler. Nessa obra, consulte as seções 1.1 Funções e 1.2 O plano das coordenadas e os gráficos, nas páginas 39 e 65, em que você poderá observar outras abordagens que complementam as discussões sobre o conceito de função, com outros exemplos, além de um estudo mais aprofundado acerca dos gráficos.

As funções afins consistem em uma das principais categorias de funções e que podem ser associadas a fenômenos que possuem comportamentos lineares. Para favorecer os estudos sobre esse tema, acesse a seção 3.7 Funções usuais, do livro Pré-Cálculo, de Francisco M. Gomes. No trecho localizado entre as páginas 277 e 279 você encontrará definições e propriedades importantes, bem como exemplos que podem auxiliar no estudo dessa categoria de funções.

Outra sugestão de material complementar é o capítulo 5, intitulado Função quadrática, do livro Matemática básica para cursos superiores, de autoria de Sebastião M. da Silva, Elio M. da Silva e Ermes M. da Silva. No trecho entre as páginas 81 a 86 você estudará conceitos essenciais associados às funções quadráticas, com destaque para a construção dos gráficos considerando seus elementos.

 

 

Referências Bibliográficas

ADAMI, A. M.; DORNELLES FILHO, A. A.; LORANDI, M. M. Pré-cálculo. Porto Alegre: Bookman, 2015.

AXLER, S. Pré-cálculo: uma preparação para o cálculo com manual de soluções para o estudante. 2. ed. Rio de Janeiro: LTC, 2016.

GOMES, F. M. Pré-cálculo: operações, equações, funções e trigonometria. São Paulo: Cengage Learning Brasil, 2018.

SAFIER, F. Pré-cálculo. 2. ed. Porto Alegre: Bookman, 2011.

SILVA, S. M. da; SILVA, E. M. da; SILVA, E. M. da. Matemática básica para cursos superiores. 2. ed. São Paulo: Atlas, 2018. 

Função exponencial

Olá, estudante! Nesta videoaula você conhecerá as propriedades das funções exponenciais, tendo em vista a definição formal de função.

Este conteúdo é importante para a sua prática profissional, pois esse tipo de função está presente em problemas que apresentam crescimentos ou decrescimentos rápidos, sendo bastante empregados em fenômenos envolvendo a proliferação de bactérias, o estudo de radiação, os problemas populacionais, entre outros contextos.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Desejamos a você boas-vindas! Nesta aula vamos investigar as características da função exponencial, tomando como referência o estudo das potências e suas propriedades, visto que essa é a base do estudo de funções dessa natureza. Analisaremos, além da definição, o comportamento gráfico dessas funções e as equações exponenciais.

Muitas são as aplicações das funções exponenciais em problemas reais, sendo uma das mais conhecidas o estudo da meia-vida de uma substância. Por exemplo, quando precisamos fazer um tratamento para a saúde com um medicamento, as dosagens e os intervalos de tempo para o consumo são calculados em função do volume corporal e sanguíneo do paciente, bem como do metabolismo e da velocidade de excreção dessa substância pelo corpo. Esse tipo de modelo também pode ser empregado em outras circunstâncias, como no estudo de fósseis, decaimento radioativo, entre outros.

A meia-vida de uma substância corresponde ao tempo necessário para que a quantidade dessa substância seja reduzida à metade da quantidade no instante anterior. Assim, se o tempo de meia-vida de um medicamento é de 8 horas, por exemplo, a cada 8 horas a quantidade de medicamento no corpo do paciente é reduzida à metade.

Suponha que um paciente ingeriu um medicamento, em dose única, por meio de um comprimido cuja concentração é de 1 g. Se a meia-vida desse medicamento é de 8 horas, e sabendo que esse comprimido é a única fonte desse medicamento no organismo do paciente, em quanto tempo a quantidade desse medicamento no corpo do paciente será de 0,015625 g, ou 15,625 mg?

Prossiga em seus estudos e confira conceitos que podem auxiliá-lo na solução dessa situação. 

Vamos Começar!

Com base no estudo das potências, podemos investigar o conceito de função exponencial. Para isso, precisamos relembrar que função corresponde a uma relação especial definida entre conjuntos, geralmente estabelecida por meio de uma regra, de modo que cada elemento do domínio esteja associado de forma única a um elemento do contradomínio. Dessa forma, vejamos a seguir as características de uma função exponencial.

Função exponencial

A função exponencial de base $a$ é definida por $f\left(x\right)=a^x$, sendo $a>0$,  $a\ne 1$ e $x$ um número real qualquer. Nesse sentido, podemos estruturar essa função da seguinte forma:

$f:\mathrm{ℝ}\to \mathrm{ℝ}$

$x\mapsto a^x, a>0 \mathrm{e} a\ne 1$

Observação: devemos exigir $a>0$ para garantir que a função esteja definida para todo $x\in \mathrm{ℝ}$, pois lembre-se de que, por exemplo, se $x=\frac{1}{2}$ então $a^{\frac{1}{2}}=\sqrt{a}$, o qual não está definido para $a$ negativo. Além disso, devemos ter $a$ diferente de 1 porque, caso contrário, teríamos a função constante $f\left(x\right)=1^x$.

Note que $x$ pode ser tanto racional quanto irracional, então são válidos todos os procedimentos envolvendo potências de expoente natural, inteiro, racional, além das aproximações obtidas pela calculadora científica para os expoentes irracionais.

Considere, por exemplo, a função $f:\mathrm{ℝ}\to \mathrm{ℝ}$ definida por ${f\left(x\right)=5}^x$. Podemos calcular as imagens para os elementos do domínio de $f$ por meio de sua lei de formação. Note que:

$f\left(5\right)=5^1=5$ $f\left(\mathrm{1,5}\right)=5^{\mathrm{1,5}}\approx \mathrm{11,18}$

$f\left(-3\right)=5^{-3}=\frac{1}{5^3}=\frac{1}{125}$ $f\left(\sqrt{3}\right){=5}^{\sqrt{3}}\approx \mathrm{16,24}$

Assim, podemos calcular imagens para qualquer elemento do domínio, sendo ele um número racional ou irracional.

Vamos agora esboçar o gráfico da função $f\left(x\right)=5^x$. Para isso, podemos construir uma tabela e identificar alguns valores de  em conjunto com suas imagens pela função $f$. Confira essas informações na Tabela 1.

$x$	-3	-2	-1	0	1
${f\left(x\right)=5}^x$	$5^{-3}=\frac{1}{125}=\mathrm{0,008}$	$5^{-2}=\frac{1}{25}=\mathrm{0,04}$	$5^{-1}=\frac{1}{5}=\mathrm{0,2}$	$5^0=1$	$5^1=5$

Dispondo os pontos da Tabela 1 em um plano cartesiano, podemos construir o gráfico, conforme apresentado na Figura 1.

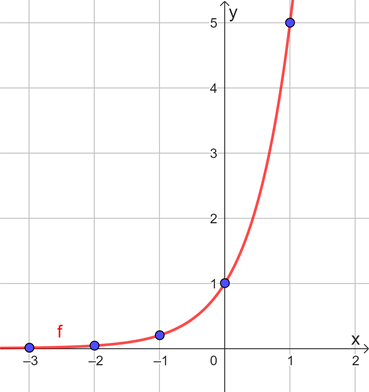
Figura 1 | Esboço para o gráfico de $f\left(x\right)=5^x$

Esse recurso da tabela pode ser utilizado na construção de gráficos de quaisquer categorias de funções, sendo interessante aliá-lo a um conhecimento prévio a respeito do perfil gráfico das diferentes funções. Vejamos na sequência um estudo mais generalizado acerca do gráfico de uma função exponencial.

Para o gráfico da função exponencial, vamos analisar dois casos. Como a base $a$ deve ser positiva e diferente de 1, vamos separar em: $0<a<1$ e $a>1$. Dessa forma, contemplamos todos os valores possíveis para a base $a$. Quando $a>1$, como é o caso de $f\left(x\right)=2^x$, ilustrada na Figura 2(a), note que. à medida que o valor de $x$ aumenta, a sua imagem $f\left(x\right)$ também aumenta, o que caracteriza a função como crescente. Nesse caso, dizemos que a função tem um crescimento exponencial.

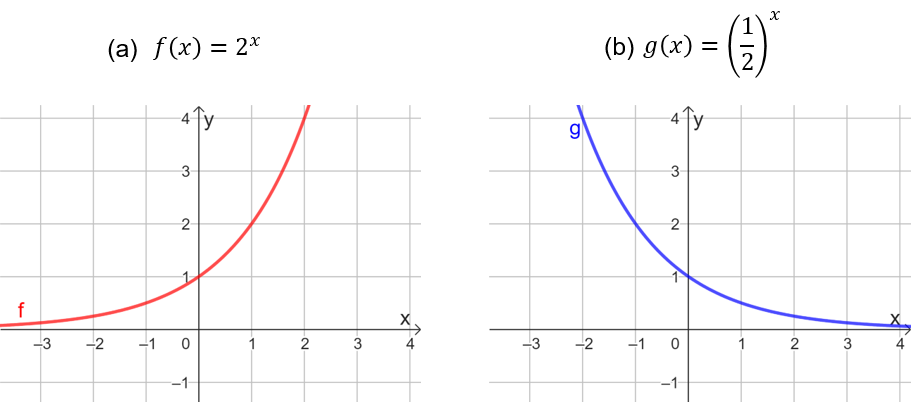
Figura 2 | Gráfico para a função exponencial

Por outro lado, no caso $0<a<1$, como em $g\left(x\right)={\left(\frac{1}{2}\right)}^x$, presente na Figura 2(b), perceba que quanto maior o valor de $x$, menor será a sua imagem $g\left(x\right)$, o que caracteriza essa função como decrescente. Assim, podemos afirmar que essa função possui decrescimento exponencial. Para ambas as situações – seja $0<a<1$ ou $a>1$ –, algumas características permanecem:

• O gráfico da função exponencial é contínuo, isto é, um traçado único.
• O domínio é o conjunto $\mathrm{ℝ}$, enquanto o conjunto imagem é dado por ${\mathrm{ℝ}}_{+}=\left(0,+\infty \right)$, basta observar que o gráfico se localiza sempre acima do eixo das abscissas.
• A interseção com o eixo $y$ ocorre no ponto $\left(\mathrm{0,1}\right)$, isto é, quando $y=1$, porém, não há interseções com o eixo $x$.

Vamos investigar as características da função $f:\mathrm{ℝ}\to \mathrm{ℝ}$ definida por $f\left(x\right)={\left(\frac{1}{3}\right)}^x$. Ela corresponde a uma função decrescente, porque sua base é um número entre 0 e 1. Podemos calcular imagens para elementos do domínio, como $f\left(0\right)={\left(\frac{1}{3}\right)}^0=1$ e $f\left(-2\right)={\left(\frac{1}{3}\right)}^{-2}={\left(\frac{3}{1}\right)}^2=9$. Também podemos fazer investigações relacionadas, por exemplo, a reconhecer qual elemento do domínio possui como imagem o número 81, o que exige o estudo de uma equação exponencial associada. Para esse caso, queremos determinar $x$ para o qual $f\left(x\right)=81$, isto é,

${\left(\frac{1}{3}\right)}^x=81 \Rightarrow {\left(3^{-1}\right)}^x=3^4 \Rightarrow 3^{-x}=3^4 \Rightarrow -x=4 \Rightarrow x=-4$

Portanto, $f\left(-4\right)=81$.

Devido às suas características, muitos estudos envolvendo as funções exponenciais exigirão a resolução de equações exponenciais, por isso é essencial conhecer as estratégias que podem ser empregadas nesses momentos. Vejamos adiante.

Siga em Frente...

Equações exponenciais

Quando em uma equação a incógnita corresponde ao expoente de uma potência, dizemos que essa é uma equação exponencial. Por exemplo, $2^x=16$ corresponde a uma equação exponencial porque nela consta uma igualdade entre duas expressões e a incógnita, $x$, corresponde ao expoente da potência de base $2$.

Para resolver uma equação exponencial, o procedimento que empregamos é a tentativa de representação dos dois membros da equação por meio de uma potência de mesma base. Isso se deve pela propriedade de que se $a>0$ e $a\ne 1$, então $a^m=a^n$ implica $m=n$. Por exemplo, no caso da equação $2^x=16$, sabemos que $16$ pode ser escrito como $2^4$, então se $2^x=2^4$ podemos concluir que $x=4$.

Vejamos outros exemplos na Tabela 2 a seguir que destacam procedimentos para a solução de equações exponenciais por meio da aplicação da propriedade apresentada.

Exemplo 1: $3^x=1$ Como $3^0=1$, então $3^x=3^0$ e, assim, $x=0$.	Exemplo 2: $5^{x-1}=125$ Temos que $125=5^3$, sendo assim, $5^{x-1}=5^3$, o que implica $x-1=3$ e, portanto, $x=4$.
Exemplo 3: ${\left(\mathrm{0,5}\right)}^x=\sqrt[3]{4}$ Note que $\mathrm{0,5}=\frac{1}{2}=2^{-1}$ e que $4=2^2$. Assim, ${\left(2^{-1}\right)}^x=\sqrt[3]{2^2} \Rightarrow 2^{-x}=2^{\frac{2}{3}} \Rightarrow -x=\frac{2}{3}$ $\Rightarrow x=-\frac{2}{3}$	Exemplo 4: $2^{x+1}+2^{x-1}=5$ Note inicialmente que essa equação pode ser reescrita como $2^x\cdot 2^1+2^x\cdot 2^{-1}=5$. Adotando $y=2^x$  obtemos: $y\cdot 2^1+y\cdot 2^{-1}=5 \Rightarrow y\cdot 2+y\cdot \frac{1}{2}=5$ $\Rightarrow \frac{5}{2}y=5 \Rightarrow y=2$ E se $y=2^x$, segue que $2=2^x$, ou $2^1=2^x$ assim, $x=1$.

Tabela 2 | Resolvendo equações exponenciais

Em todos os exemplos apresentados na Tabela 1, apesar das equações apresentarem padrões diferentes, o objetivo sempre foi a busca pela representação de cada membro da igualdade como uma potência de mesma base, ou a mudança de variáveis para que, ao final, fosse possível comparar potências de mesma base.

As equações exponenciais podem estar presentes durante o estudo de uma função exponencial. Por exemplo, considere a função $f:\mathrm{ℝ}\to \mathrm{ℝ}$ definida por $f\left(x\right)={\left(\frac{1}{4}\right)}^x$. Observe que podemos escrever a lei de formação dessa função como $f\left(x\right)={\left(\frac{1}{4}\right)}^x$, na forma $f\left(x\right)=4^{-x}$, ou ainda $f\left(x\right)={\left(\mathrm{0,25}\right)}^x$. Essas representações são possíveis a partir das diferentes representações para os números e das definições e propriedades de potências. Queremos determinar o valor do domínio $x$ para o qual $f\left(x\right)=256$, assim, o objetivo é a resolução da equação exponencial ${\left(\frac{1}{4}\right)}^x=256$. A fatoração pode ser utilizada nesse caso, com o intuito de identificar potências cujo resultado é 256. Vejamos que $256=4\cdot 4\cdot 4\cdot 4=4^4$. Como ${\left(\frac{1}{4}\right)}^x=256=4^4$, então $4^{-x}=4^4$, logo, $-x=4$ ou $x=-4$. Portanto, $f\left(-4\right)=256$.

A seguir, vejamos um estudo da função exponencial tomando como base o número $e$, bastante empregado em problemas das ciências naturais.

Função exponencial de base $\mathit{e}$

O número $e$, chamado de número de Euler, corresponde a um número irracional cujo valor aproximado com cinco casas decimais é 2,71828. Geralmente as calculadoras científicas trazem um botão com a função $e^x$, relacionada a esse número, que, no entanto, pode ser definido por meio de um conceito conhecido como limite, por meio da expressão $e=\underset{n\to \infty }{\lim }{\left(1+\frac{1}{n}\right)}^n$.

A partir do número $e$, podemos construir a função exponencial de base $e$ dada por $f\left(x\right)=e^x$. Sendo $e>1$, podemos concluir que essa função é crescente, intersecta o eixo $y$ em $y=1$ e não tem interseção com o eixo $x$. Veja na Figura 3.

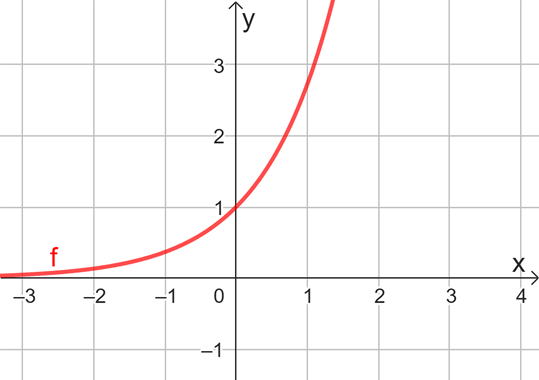
Figura 3 | Gráfico da função exponencial de base $e$

Em alguns contextos, a função exponencial de base  também é apresentada como $f\left(x\right)=\exp \left(x\right)$. Pelas suas propriedades, a função exponencial de base $e$ é bastante empregada na construção de modelos matemáticos, facilitando inclusive o emprego de procedimentos algébricos e numéricos.

Assim, de posse das propriedades das funções exponenciais, podemos estudar diversos fenômenos, desde que eles apresentem características que se assemelham às da função exponencial, seja ela crescente ou decrescente. 

Vamos Exercitar?

Retornando ao problema do medicamento, temos que o tempo de meia-vida da substância é de 8 horas. Além disso, sua concentração inicial é de 1 g. Veja na Tabela 3 uma análise sobre a evolução da quantidade dessa substância no corpo do paciente após  períodos de 8 horas, ou seja, após  períodos de meia-vida.

$x$	0	1	2	3
Quantidade da substância $\left(q\right)$	1	$\frac{1}{2}$	$\frac{\left(\frac{1}{2}\right)}{2}=\frac{1}{4}$	$\frac{\left(\frac{1}{4}\right)}{2}=\frac{1}{8}$

Tabela 3 | Evolução da quantidade de medicamento no corpo do paciente

Podemos expressar a quantidade de substância $\left(q\right)$ em função da quantidade de períodos de meia-vida $\left(x\right)$ a partir da função exponencial:

$q\left(x\right)={\left(\frac{1}{2}\right)}^x$

A função $q$ tem base $0<\frac{1}{2}<1$, logo, corresponde a uma função decrescente. Queremos determinar $x$ para o qual $q\left(x\right)=\mathrm{0,015625}$, isto é,

$\mathrm{0,015625}={\left(\frac{1}{2}\right)}^x \Rightarrow \frac{1}{64}={\left(\frac{1}{2}\right)}^x \Rightarrow \frac{1}{2^6}={\left(\frac{1}{2}\right)}^x \Rightarrow {\left(\frac{1}{2}\right)}^6={\left(\frac{1}{2}\right)}^x \Rightarrow x=6$

Assim, após 6 períodos de meia-vida a quantidade dessa substância será 0,015625 g. Como 6 períodos de 8 horas correspondem a 48 horas, então após dois dias a quantidade de medicamento no organismo do paciente será de 0,015625 g. 

Saiba Mais

Como sugestão para aprofundamento dos estudos sobre funções exponenciais, consulte o livro Fundamentos de matemática para engenharias e tecnologias, de Giácomo A. Bonetto e Afrânio C. Murolo. Na seção 5.1, Função exponencial, localizada entre as páginas 108 e 111, bem como na seção 5.4, Função exponencial com base e, entre as páginas 120 e 123, você encontrará informações básicas sobre as funções exponenciais, inclusive as de base , com exemplos.

Outro material que contempla o estudo das características das funções exponenciais é o livro Pré-Cálculo, de Thamara Petroli. Na seção Função exponencial, entre as páginas 125 e 128, você encontrará detalhes sobre a função exponencial, principalmente em relação às propriedades analisadas em conjunto com os gráficos correspondentes.

Outra referência no estudo das funções é o livro Cálculo – volume 1, de George B. Thomas, Maurice. D. Weir e Joel Hass. Nessa obra, na seção 1.5, Funções exponenciais, localizada entre as páginas 32 e 36, você estudará as principais definições vinculadas a essa categoria de funções, inclusive com aplicações delas na resolução de problemas diversos.

 

 

Referências Bibliográficas

ADAMI, A. M.; DORNELLES FILHO, A. A.; LORANDI, M. M. Pré-cálculo. Porto Alegre: Bookman, 2015.

BONETTO, G. A.; MUROLO, A. C. Fundamentos de matemática para engenharias e tecnologias. São Paulo: Cengage Learning Brasil, 2018.

GOMES, F. M. Pré-cálculo: operações, equações, funções e trigonometria. São Paulo: Cengage Learning Brasil, 2018.

PETROLI, T. Pré-cálculo. 1. ed. São Paulo: Contentus, 2020.

THOMAS, G. B.; WEIR, M. D.; HASS, J. Cálculo. 12. ed. São Paulo: Pearson, 2012.

Função logarítmica

Olá, estudante! Nesta videoaula você conhecerá a função logarítmica e suas propriedades, tendo como referência o conceito de logaritmo, a relação entre logaritmos e potências, bem como a função exponencial, já que podemos estabelecer uma relação importante entre essas funções.

Este conteúdo é importante para a sua prática profissional, pois além das aplicações específicas das funções logarítmicas, a sua relação com as exponenciais permite ampliar a gama de problemas que podem ser estudados.

Prepare-se para essa jornada de conhecimento!

Ponto de Partida

Estudante, desejamos boas-vindas a você! Nesta aula vamos explorar as propriedades das funções logarítmicas, bem como sua relação com as funções exponenciais, além de conhecer propriedades para a resolução de equações logarítmicas.

É importante ressaltar que, assim como existem critérios para definir um logaritmo, também precisamos considerá-los no momento de definir uma função logarítmica. Ainda, as propriedades dos logaritmos também estão presentes nessa categoria de função.

Para complementar os estudos acerca da temática apresentada, vamos analisar o seguinte problema. O decaimento radioativo da substância césio-137 é dado, ao longo do tempo  dado em anos, pela função:

$Q\left(t\right)=Q_0\cdot e^{-\mathrm{0,023105}t}$

em que $Q_0$ representa a massa inicial e $Q\left(t\right)$, a massa no instante $t$. De posse dessas informações, qual o tempo mínimo necessário para que a quantidade de césio-137 seja reduzida à metade da quantidade inicial?

Prossiga em seus estudos e conheça as propriedades da função logarítmica e sua relação com a função exponencial. 

 

Vamos Começar!

Uma função é definida a partir de uma relação especial entre dois conjuntos, sendo geralmente representada pela sua lei de formação, e em muitos casos apresentados em sua forma gráfica. Diante dessa definição, vejamos a seguir quais são as especificidades da função logarítmica.

Função logarítmica

Uma função logarítmica de base $a$ consiste em uma função $f:{\mathrm{ℝ}}_{+}^{*}\to \mathrm{ℝ}$ definida por

$f\left(x\right)={\log }_{a}x$

com $a>0$ e $a\ne 1$. Sabemos que o logaritmando precisa ser um número positivo, por isso devemos restringir o domínio da função a ${\mathrm{ℝ}}_{+}^{*}$, ou seja, ao conjunto formado pelos números reais positivos. Note que as restrições para a definição de logaritmo devem estar presentes na definição da função logarítmica.

Por exemplo,  $f:{\mathrm{ℝ}}_{+}^{*}\to \mathrm{ℝ}$ definida por $f\left(x\right)={\log }_{2}x$ é uma função logarítmica construída a partir da base 2. Nesse caso,

• $f\left(2\right)=1$, porque ${\log }_{2}2=1$.
• $f\left(4\right)=2$, porque ${\log }_{2}4=2$.
• $f\left(128\right)=7$, porque ${\log }_{2}128=7$, visto que $2^7=128$.

Vamos analisar o comportamento gráfico da função logarítmica. Essa função tem seu gráfico descrito pela chamada curva logarítmica. Além disso, como o domínio é dado apenas pelos números reais $x$ positivos, seu gráfico está sempre à direita do eixo $y$. E como ${\log }_{a}1=0$, há interseção do gráfico da função logarítmica $f\left(x\right)={\log }_{a}x$ com o eixo $x$ no ponto $\left(\mathrm{1,0}\right)$.

Para analisar os detalhes do gráfico da função logarítmica, principalmente em relação ao crescimento e decrescimento, sendo $f\left(x\right)={\log }_a\left(x\right)$, como $a>0$ e $a\ne 1$, podemos fazer um estudo separado em duas categorias: $0<a<1$ e $a>1$. Para o primeiro caso, como em $f\left(x\right)={\log }_{\frac{1}{3}}x$, a função será decrescente, assumindo, portanto, um decrescimento logarítmico, conforme Figura 1(a). Por outro lado, quando $a>1$, como em $g\left(x\right)={\log }_{3}x$, a função é crescente e, assim, seu comportamento é de crescimento logarítmico, exibido na Figura 1(b).

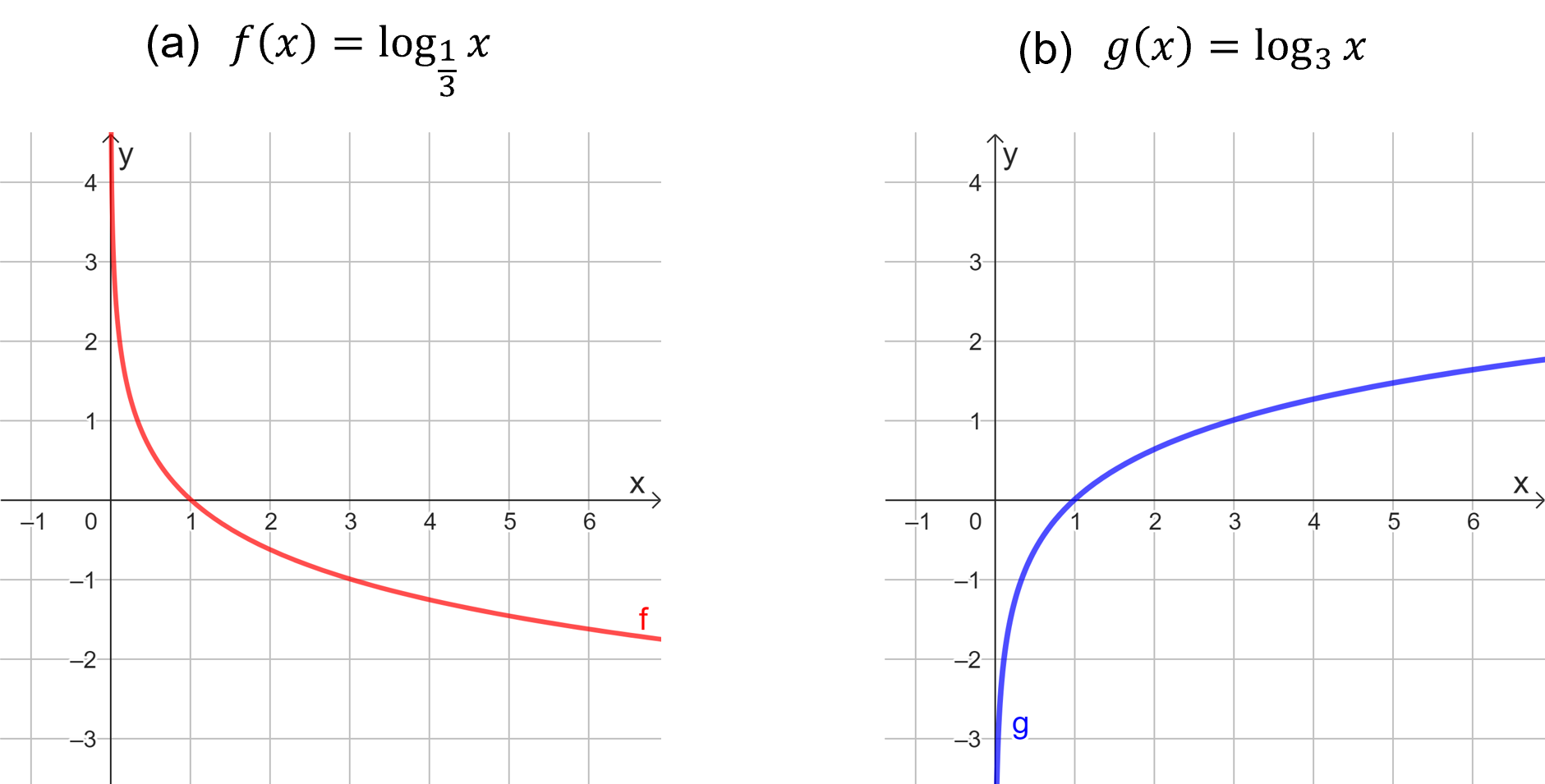
Figura 1 | Gráfico para a função logarítmica

Observe que as funções $f$ e $g$, da Figura 1, intersectam o eixo $x$ no ponto de coordenadas $\left(\mathrm{1,0}\right)$ e tem seus gráficos definidos apenas para valores positivos de $x$. Essas características podem ser observadas para qualquer função logarítmica na forma $f\left(x\right)={\log }_{a}x$, desde que $a>0$, $a\ne 1$, e com $x>0$ pela definição do domínio.

Assim como definimos logaritmo decimal (base 10) e natural (base $e$), também podemos definir as funções correspondentes. Na Figura 2 você poderá observar os gráficos das duas funções, sendo $f\left(x\right)=\log x$ a função construída a partir da base 10 e a função $g\left(x\right)=\ln x$, construída a partir da base $e$.

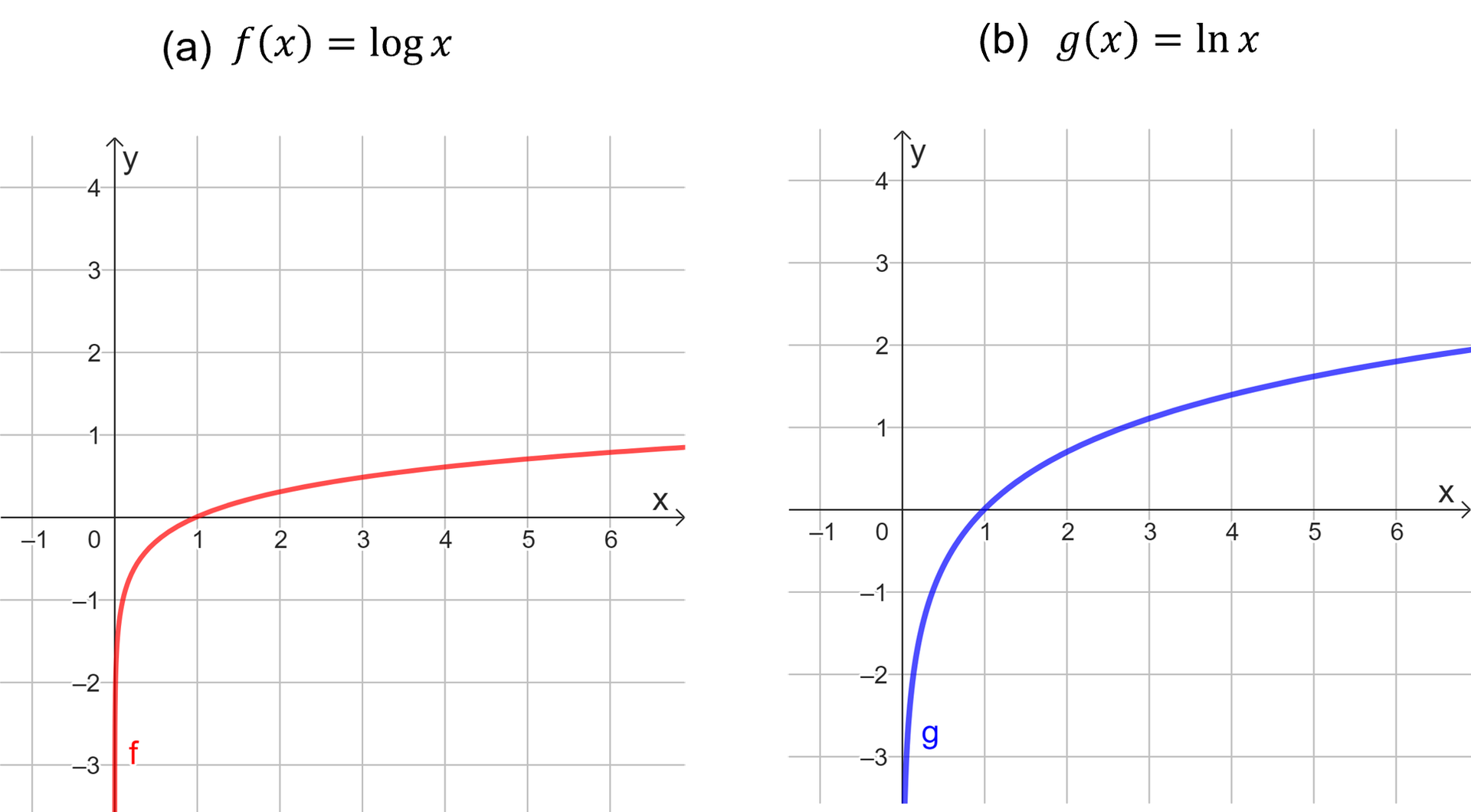
Figura 2 | Gráficos das funções logarítmicas decimal e natural

Considerando a Figura 2, observe que tanto $f\left(x\right)=\log x$ quanto $g\left(x\right)=\ln x$ são funções crescentes, visto que suas bases são números maiores do que 1.

Podemos aplicar sobre os logaritmos uma propriedade de mudança de base. Para isso, suponha que precisamos efetuar o cálculo de ${\log }_{a}b$, com $a>0$, $a\ne 1$ e $b>0$. Porém, precisamos modificar a base do logaritmo para $c$, com $c>0$ e $c\ne 1$. Assim, a mudança de base nos diz que:

${\log }_{a}b=\frac{{\log }_{c}b}{{\log }_{c}a}$

Essa propriedade é bastante utilizada principalmente quando precisamos realizar estudos com suporte da calculadora científica, a qual só trabalha nas bases 10 e $e$. Por exemplo, utilizando uma calculadora científica, vamos calcular ${\log }_{3}12$. Para isso, adotando a base 10 e empregando a mudança de base, segue que:

${\log }_{3}12=\frac{\log 12}{\log 3}\approx \frac{\mathrm{1,079}}{\mathrm{0,477}}\approx \mathrm{2,262}$

Esse tipo de propriedade pode ser empregado em conjunto com o estudo das funções logarítmicas, como no caso das imagens de funções, por exemplo.

No tópico a seguir, vamos comparar as funções exponencial e logarítmica, observando as relações que podemos estabelecer entre elas.

Relações entre função exponencial e logarítmica

As funções exponencial e logarítmica de mesma base podem ser associadas entre si, assim como percebido entre potências e logaritmos. Para isso, vamos analisar o caso das funções $f\left(x\right)=2^x$ e $g\left(x\right)={\log }_{2}x$, cujos gráficos são indicados na Figura 3.

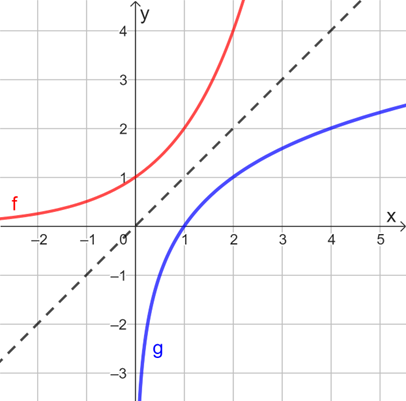
Figura 3 | Gráficos das funções exponencial $f$e logarítmica $g$

No gráfico da Figura 3 também foi traçada uma reta, tracejada, que representa a função $p\left(x\right)=x$. Observe que os gráficos das funções $f$ e $g$ são simétricos em relação a essa reta. Esse fato é observado em outras comparações, mas desde que as duas funções – exponencial e logarítmica – sejam construídas a partir da mesma base $a$, com $a>0$ e $a\ne 1$. Dessa forma, pelas características dessas funções, podemos afirmar que elas são inversas uma da outra.

Analisando ainda a Figura 3, além da simetria, podemos identificar que a função $f$ possui interseção com o eixo $y$, enquanto $g$ tem interseção com o eixo $x$, além de que ambas as funções são crescentes, porque a base é igual a 2, isto é, um número maior do que 1.

Os comparativos também poderiam ser feitos entre outros pares de funções, como $m\left(x\right)={\left(\frac{1}{3}\right)}^x$ e $n\left(x\right)={\log }_{1/3}\left(x\right)$, por exemplo, mas desde que as bases sejam iguais. Nesse caso, a única diferença entre as observações é que ambas as funções são decrescentes, porque a base é um número entre 0 e 1.

Pelas relações estabelecidas entre as funções exponenciais e logarítmicas, e de posse de suas propriedades, podemos empregá-las nos mais variados estudos, considerando sua aplicabilidade em contextos de diferentes áreas do conhecimento.

Durante o estudo das funções logarítmicas, podemos nos deparar com equações envolvendo esse tipo de termo, então, adiante, vejamos como resolver esse tipo de equação.

Siga em Frente...

Resolvendo equações logarítmicas

Uma equação logarítmica corresponde a uma igualdade na qual a incógnita é apresentada no logaritmando ou na base de um logaritmo, ou ainda, em ambos os termos. Por exemplo, ${\log }_2(x-1)=5$ e ${\log }_{x}3=1$ são exemplos de equações logarítmicas. Outro exemplo que podemos destacar é ${\log }_{x-2}(3x+1)=2$, sendo que nesse caso a incógnita $x$ está presente tanto na base quanto no logaritmando.

Por exemplo, para equações semelhantes a ${\log }_{2}x=3$, basta aplicarmos a definição de logaritmo em sua resolução. Para esse caso,

${{\log }_{2}x=3 \iff 2}^3=x \iff x=8$

Um procedimento semelhante se aplica quando tivermos uma equação como ${\log }_{x}4=2$.

${\log }_{x}4=2 \iff x^2=4 \iff x=\pm \sqrt{2} \iff x=\pm 2$

Como $x$ representa a base, e não podemos ter base negativa, então a única solução para essa equação é $x=2$. Essa avaliação é essencial para que sejam verificadas as condições de existência do logaritmo.

Os procedimentos anteriores decorrem diretamente da definição de logaritmo. Porém, podemos nos deparar com outras situações. Os logaritmos possuem como uma de suas propriedades a injetividade, isto é, dado ${\log }_{a}x$, com $a>0$ e $a\ne 1$, é válida a seguinte propriedade: ${\log }_{a}x={\log }_{a}y$ equivale a $x=y$. Com isso, podemos construir estratégias que permitam a resolução de alguns tipos de equações logarítmicas.

Por exemplo, para resolver a equação ${\log }_2\left(x-2\right)={\log }_2\left(3x+5\right)$, como ambos os membros estão construídos a partir de logaritmos de mesma base, basta igualarmos os logaritmandos:

${\log }_2\left(x-2\right)={\log }_2\left(3x+5\right) \iff x-2=3x+5 \iff x-3x=5+2$

$\iff -2x=7 \iff x=-\frac{7}{2}$

Outra possibilidade envolve uma propriedade que associa potências e logaritmos: $a^{{\log }_{a}x}=x$. Como exemplo, vamos resolver $\log (2x+100)=3$. Seguem os procedimentos:

$\log (2x+100)=3 \iff {10}^{\log (2x+100)}={10}^3 \iff 2x+100=1000 \iff 2x=900 \iff x=450$

Logo, a solução é $x=450$.

Vejamos outro exemplo. Agora, para ${\log }_2\left(4x\right)-{\log }_2\left(12\right)=5$.

${\log }_2\left(4x\right)-{\log }_2\left(12\right)=5 \iff {\log }_2\left(4x\right)=5+{\log }_2\left(12\right) \iff 2^{{\log }_{2}4x}=2^{5+{\log }_2\left(12\right)}$

$\iff 2^{{\log }_{2}4x}={2^5\cdot 2}^{{\log }_2\left(12\right)} \iff 4x=32\cdot 12 \iff 4x=384 \iff x=\frac{384}{4}=96$

Portanto, a solução é $x=96$.

Podemos ainda empregar o conceito de logaritmo para a resolução de equações exponenciais considerando a propriedade que envolve a igualdade entre logaritmos de mesma base, ou seja, ${\log }_{a}x={\log }_{a}y\iff x=y$, para $a>0$ e $a\ne 1$. Vejamos o caso da equação exponencial $2^x=3$. Utilizando a propriedade citada, se essa igualdade é válida, então também será válido que ${\log }_a{2}^x={\log }_{a}3$, com $a>0$ e $a\ne 1$. Se fossemos empregar a base 10 e a calculadora científica como suporte, a solução da equação exponencial seria dada por:

$2^x=3 \iff \log 2^x=\log 3 \iff x\cdot \log 2=\log 3$

Como $\log 2$ e $\log 3$ são números, a última equação obtida pode ser classificada como uma equação polinomial de 1º grau. Assim, perceba que o emprego da propriedade dos logaritmos permite a conversão de uma equação exponencial em uma equação de 1º grau, a qual pode ser resolvida isolando a incógnita em um dos membros da equação. Prosseguindo com a resolução, obtemos:

$x\cdot \log 2=\log 3 \iff x=\frac{\log 3}{\log 2}\approx \frac{\mathrm{0,477}}{\mathrm{0,301}}\approx \mathrm{1,58}$

Portanto, a solução de $2^x=3$ é, aproximadamente, $x=\mathrm{1,58}$.

Vejamos um outro exemplo. Para resolver a equação $3^{2x}=8$, recorrendo à base 3, teremos:

$3^{2x}=8 \iff {\log }_3{3}^{2x}={\log }_{3}8 \iff 2x={\log }_{3}8$

Não conseguimos determinar o valor de ${\log }_{3}8$ utilizando a calculadora científica. Por isso, apliquemos uma mudança de base:

${\log }_{3}8=\frac{\log 8}{\log 3}\approx \frac{\mathrm{0,903}}{\mathrm{0,477}}\approx \mathrm{1,89}$

Substituindo esse resultado em $2x={\log }_{3}8$ teremos:

$2x=\mathrm{1,89}\iff x=\frac{\mathrm{1,89}}{2}=\mathrm{0,945}$

Logo, a solução aproximada para $3^{2x}=8$ é $x=\mathrm{0,945}$.

Note que cada equação possui suas especificidades, porém, existem muitos padrões que se repetem nas resoluções. Por isso, é importante observar as características de cada equação, identificando as estratégias que podem ser utilizadas em cada caso, sem esquecer que as condições de existência dos logaritmos precisam ser verificadas.  

Vamos Exercitar?

Retomando o problema apresentado, o decaimento radioativo do césio-137 é dado, ao longo do tempo $t$ dado em anos, pela função exponencial:

$Q\left(t\right)=Q_0\cdot e^{-\mathrm{0,023105}t}$

em que $Q_0$ representa a massa inicial e $Q\left(t\right)$, a massa no instante $t$.

Reescrevendo a função de tal forma a representar $t$ em função de $Q$, obtemos:

$\frac{Q}{Q_0}=e^{-\mathrm{0,023105}t} \Rightarrow \ln \left(\frac{Q}{Q_0}\right)=\ln \left(e^{-\mathrm{0,023105}t}\right)$

$\Rightarrow -\mathrm{0,023105}t=\ln \left(\frac{Q}{Q_0}\right) \Rightarrow t=-\frac{\ln \left(\frac{Q}{Q_0}\right)}{\mathrm{0,023105}}$

Logo, temos a função inversa da função original, dada por $t\left(Q\right)=-\frac{\ln \left(\frac{Q}{Q_0}\right)}{\mathrm{0,023105}}$, a qual expressa agora o tempo em função da massa, sendo do tipo logarítmica.

Queremos determinar o tempo mínimo para que a quantidade de césio-137 seja reduzida à metade da quantidade inicial, isto é, determinar $t$ para o qual $Q=\frac{Q_0}{2}$, isto é,

$t\left(\frac{Q_0}{2}\right)=-\frac{\ln \left(\frac{\frac{Q_0}{2}}{Q_0}\right)}{\mathrm{0,023105}} \Rightarrow t\left(\frac{Q_0}{2}\right)=-\frac{\ln \left(\frac{1}{2}\right)}{\mathrm{0,023105}} \Rightarrow t\left(\frac{Q_0}{2}\right)\approx 30$

Portanto, o tempo mínimo necessário é de 30 anos, o que conclui a solução do problema. 

Saiba Mais

Como sugestão para complementação dos estudos sobre funções logarítmicas, temos o livro Cálculo – volume 1, de James Stewart, Daniel Clegg e Saleem Watson. Na seção 1.5 Funções inversas e logaritmos, no trecho entre as páginas 49 e 53, o qual inicia no tópico Funções logarítmicas e vai até o tópico Gráfico e crescimento do logaritmo natural, podemos retomar conceitos importantes como as propriedades e a mudança de base, bem como aprofundar os estudos na definição da função logarítmica e, mais especificamente, do estudo do logaritmo natural.

Outra sugestão é o livro Fundamentos de matemática para engenharias e tecnologias, de Giácomo A. Bonetto e Afrânio C. Murolo. Consulte a seção 7.3 Função logaritmica, entre as páginas 162 e 164, para explorar a definição de função logarítmica, bem como aprofundar os estudos sobre os gráficos e suas características. Já na seção 7.4 Aplicações, entre as páginas 165 e 168, você poderá consultar algumas aplicações importantes, como o emprego no estudo de pH de solução aquosa, terremotos, problemas de meia-vida, entre outros.

Uma sugestão de material complementar a respeito de logaritmos é a obra Pré-Cálculo, de Fred Safier. Nesse material, é proposta uma discussão sobre resoluções de equações exponenciais e logarítmicas, bem como retomada da mudança de base, inclusive com exercícios resolvidos, no trecho entre as páginas 168 e 174, em seu capítulo 19 Equações exponenciais e logarítmicas.

 

 

Referências Bibliográficas

ADAMI, A. M.; DORNELLES FILHO, A. A.; LORANDI, M. M. Pré-cálculo. Porto Alegre: Bookman, 2015.

BONETTO, G. A.; MUROLO, A. C. Fundamentos de matemática para engenharias e tecnologias. São Paulo: Cengage Learning Brasil, 2018.

GOMES, F. M. Pré-cálculo: operações, equações, funções e trigonometria. São Paulo: Cengage Learning Brasil, 2018.

SAFIER, F. Pré-cálculo. Porto Alegre: Bookman, 2011.

STEWART, J.; CLEGG, D.; WATSON, S. Cálculo: Volume I. Tradução da 9. Ed. norte-americana. São Paulo: Cengage Learning Brasil, 2021. 

Função trigonométrica

Olá, estudante! Nesta videoaula você conhecerá as principais funções trigonométricas, com suas propriedades, tendo como referência os estudos de trigonometria desenvolvidos sobre o triângulo retângulo.

Este conteúdo é importante para a sua prática profissional, pois podemos empregar as funções trigonométricas na modelagem de problemas relativos a fenômenos periódicos, ajustando conforme as características de cada situação, como é o caso dos batimentos cardíacos, variação das marés, entre outros.

Prepare-se para essa jornada de conhecimento! Vamos lá!

Ponto de Partida

Nesta aula o objetivo é estudar as funções trigonométricas, tendo em vista a articulação entre o conceito de função, o ciclo ou o círculo trigonométrico e o estudo das razões trigonométricas definidas no triângulo retângulo.

Nesse sentido, daremos início ao estudo do ciclo trigonométrico, a partir do qual podemos estudar as razões trigonométricas seno, cosseno e tangente para qualquer ângulo. É importante ressaltar que nesse momento priorizaremos os ângulos medidos em radianos. De posse desses conhecimentos, concluiremos nosso estudo investigando os comportamentos das funções seno, cosseno e tangente, tendo em vista principalmente a sua aplicação na modelagem de fenômenos periódicos.

Diante desse tema, vamos refletir a respeito do seguinte problema. Considere que a quantidade de clientes que frequentam diariamente um supermercado, aberto 24 horas por dia, apresenta um comportamento periódico em função do tempo. Fazendo um levantamento da quantidade $C$ de clientes no tempo $x$, em horas, suponha que foi possível construir o modelo:

$C\left(x\right)=1000-700\cdot \mathrm{sen}\left(\frac{\pi \cdot x}{12}\right)$

considere que $t$ é um inteiro tal que $0\le x\le 24$.

Analisando esse modelo, em quais horários a quantidade de clientes assumiu seu valor máximo? E seu valor mínimo? Como podemos solucionar esse problema? Confira a seguir os conceitos essenciais para esse estudo. 

Vamos Começar!

As razões trigonométricas seno, cosseno e tangente podem ser estudadas por meio de uma associação com os triângulos retângulos e suas propriedades. No entanto, podemos adequar esse estudo com o objetivo de trabalhar com as medições dos ângulos e das razões utilizando circunferências, bem como construir funções derivadas delas. Para isso, iniciemos com o estudo do ciclo ou da circunferência trigonométrica no tópico a seguir, lembrando da correspondência $\pi rad=180°$, visto que precisaremos trabalhar com os ângulos em radianos.

Ciclo trigonométrico ou circunferência trigonométrica

Para estudar os valores assumidos por seno, cosseno e tangente de diferentes ângulos, podemos utilizar o ciclo trigonométrico, conhecido também por circunferência trigonométrica. Esse ciclo é construído, no plano cartesiano, a partir de uma circunferência centrada na origem $O\left(\mathrm{0,0}\right)$ e de raio com medida igual a uma unidade, conforme a Figura 1. Os eixos coordenados dividem o círculo em quatro quadrantes, sendo o 1º quadrante o que inclui os ângulos no intervalo $0°<\alpha <90°$, o 2º quadrante inclui os ângulos no intervalo $90°<\alpha <180°$, o 3º quadrante inclui os ângulos no intervalo $180°<\alpha <270°$ e o 4º quadrante inclui os ângulos no intervalo $270°<\alpha <360°$, finalizando novamente no ponto $A\left(\mathrm{1,0}\right)$, como na Figura 1(b).

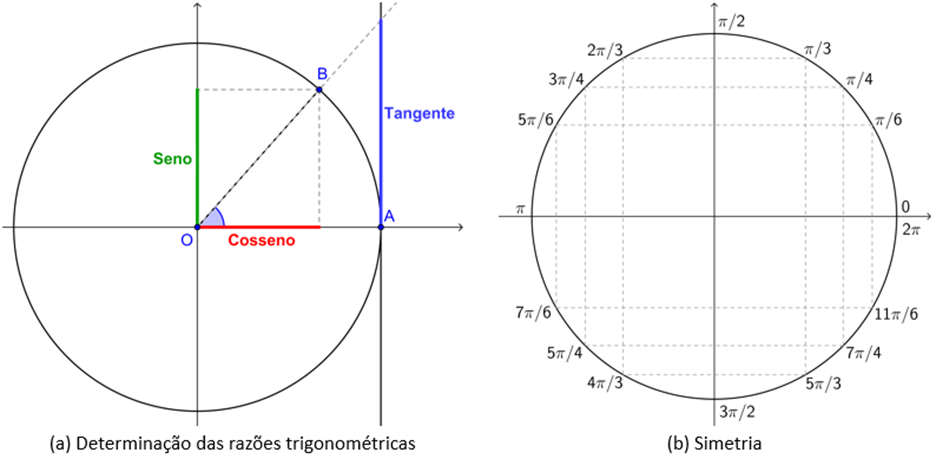
Figura 1 | Ciclo trigonométrico

Percorremos o ciclo no sentido anti-horário, partindo do eixo $x$, mais especificamente do ponto de coordenadas $A\left(\mathrm{1,0}\right)$, de acordo com a Figura 1(a), por meio da construção de arcos centrados na origem. Para um arco $\widehat{AOB}$, como o exemplo ilustrado na Figura 1(a), o valor do seno do ângulo central associado é dado pela distância entre o centro $O$ da circunferência e a projeção do ponto $B$ sobre o eixo $y$ (vertical), enquanto o cosseno é dado pela distância entre $O$ e a projeção do ponto $B$ sobre o eixo x (horizontal), isto é, os valores de seno são avaliados sobre o eixo y e os de cosseno sobre o eixo x, de modo que em ambos os casos os valores variam de -1 a 1, limitados pela circunferência cujo raio tem medida uma unidade. A tangente é avaliada em uma reta tangente à circunferência, que contém o ponto $A\left(\mathrm{1,0}\right)$ e é perpendicular ao eixo $x$. Assim, para o ângulo destacado na Figura 1(a), a tangente consiste na distância do ponto $A$ até o ponto de interseção entre a reta tangente e a reta que contém os pontos $O$ e $B$.

No estudo do ciclo trigonométrico, podemos destacar alguns ângulos, chamados ângulos notáveis: $\frac{\pi }{6}$,  $\frac{\pi }{4}$ e $\frac{\pi }{3}$ radianos. Além deles, podemos definir os ângulos correspondentes a $0$, $\frac{\pi }{2}$, $\pi$,  $\frac{3\pi }{2}$ e $2\pi$ radianos. Podemos ainda identificar os simétricos a eles em relação aos eixos $x$ e $y$, conforme ângulos destacados na Figura 1(b), o que permite comparar os valores de seno, cosseno e tangente dos simétricos por meio da identificação dos sinais associados a cada quadrante. Veja na Tabela 1 os valores de seno, cosseno e tangente para os ângulos citados.

Ângulos	0° ou 0 rad	30° ou  $\frac{\mathit{\pi }}{6}$rad	45° ou  $\frac{\mathit{\pi }}{4}$rad	60° ou  $\frac{\mathit{\pi }}{3}$rad	90° ou  $\frac{\mathit{\pi }}{2}$rad	180° ou $\mathit{\pi }$rad	270° ou  $\frac{3\mathit{\pi }}{2}$rad	360° ou  $2\mathit{\pi }$rad
Seno	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$	$0$	$-1$	$0$
Cosseno	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$	$-1$	$0$	$1$
Tangente	$1$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$	$\nexists$	$0$	$\nexists$	$0$

Tabela 1 | Valores das razões trigonométricas para ângulos notáveis. Fonte: Gomes (2018, p. 466).

Veja que $tg\left(90°\right)$ e $tg\left(270°\right)$ não estão definidas ($\nexists$). Basta lembrar que $tg\left(\alpha \right)=\frac{sen\left(\alpha \right)}{\cos \left(\alpha \right)}$ e que, para os dois ângulos citados, o cosseno é nulo, o que impossibilita efetuar a divisão por zero para cálculo da tangente.

Com base nas razões apresentadas, e a estrutura do ciclo trigonométrico, podemos construir as funções seno, cosseno e tangente, cujos detalhes serão apresentados no que segue.

Siga em Frente...

Funções trigonométricas

A função $f:\mathrm{ℝ}\to \mathrm{ℝ}$ chamada de função seno é dada por $f\left(x\right)=\mathrm{sen}\left(x\right)$. Seu gráfico é descrito por uma curva do tipo senoide e é dada conforme a Figura 2(a). A função seno é periódica de período $2\pi$, basta observar que o comportamento de seu gráfico se repete a cada intervalo de comprimento $2\pi$. Além disso, a função tem sua imagem limitada e descrita pelo intervalo $Im\left(f\right)=\left[-\mathrm{1,1}\right]$. Isso se deve ao fato de que os valores de seno no ciclo trigonométrico variam de -1 a 1. O gráfico pode ser analisado com base nos dados da Tabela 1.

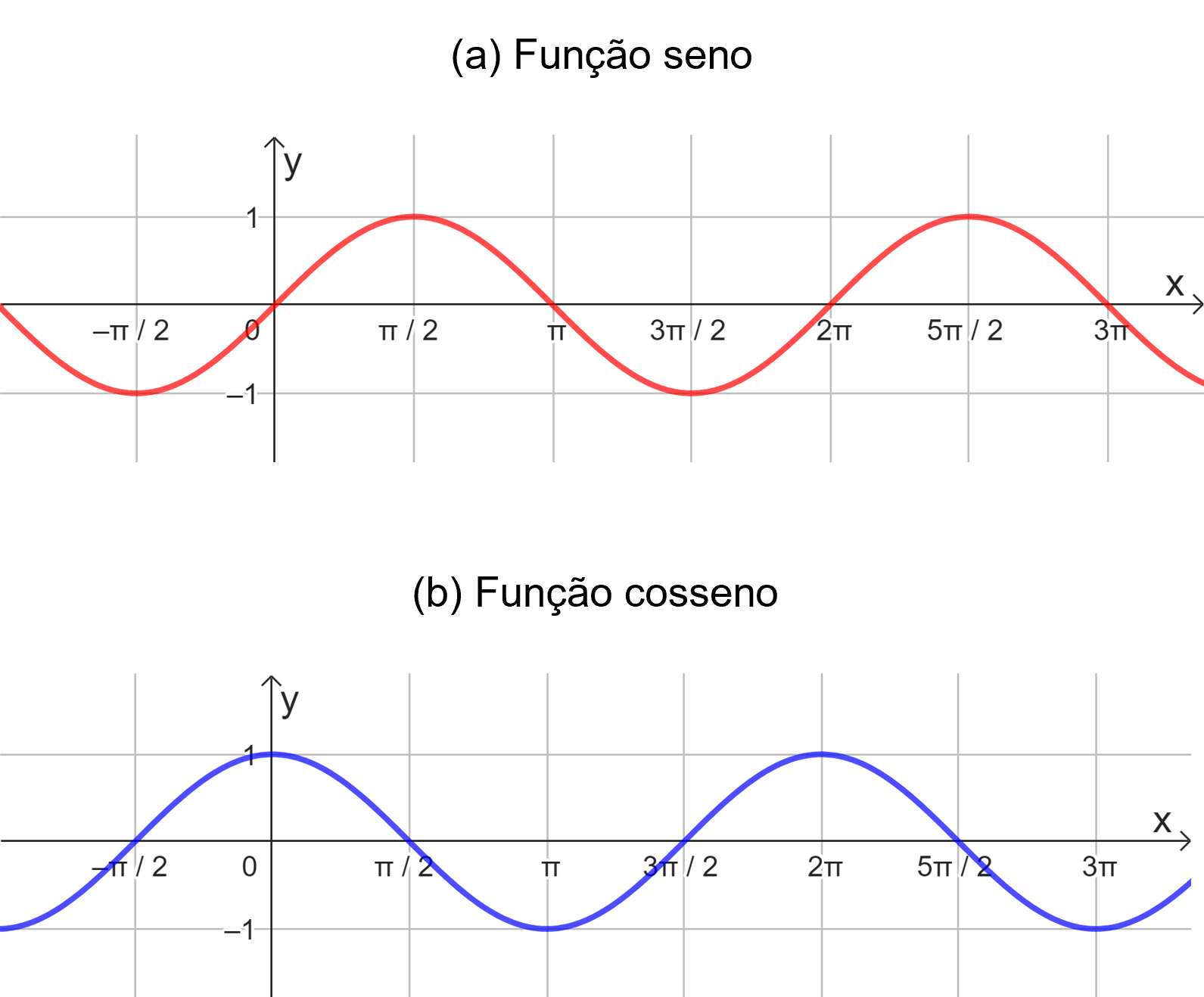
Figura 2 | Gráficos das funções trigonométricas

Por outro lado, a função cosseno é dada por $g:\mathrm{ℝ}\to \mathrm{ℝ}$ em que $g\left(x\right)=\cos \left(x\right)$, cujo gráfico é dado na Figura 2(b). Essa função é também periódica de período $2\pi$, apresentando também limitação em sua imagem com $Im\left(g\right)=\left[-\mathrm{1,1}\right]$. Veja a associação entre o gráfico e os dados da Tabela 1.

As funções seno e cosseno são usualmente aplicadas no estudo de problemas que envolvem periodicidade. No entanto, em muitos casos precisamos fazer modificações no gráfico original para atender às propriedades do problema em estudo. Vejamos a seguir de que forma essas modificações influenciam nas características dessas funções, tomando como referência a função seno, mas sabendo que a cosseno apresenta comportamento semelhante.

Nesse sentido, seja a função original $f\left(x\right)=\mathrm{sen}\left(x\right)$ e $g\left(x\right)=a+b\cdot \mathrm{sen}\left(c\cdot x+d\right)$, sendo domínio e contradomínio reais para ambas. Analisemos o papel de cada um dos parâmetros $a,b,c,d\in \mathrm{ℝ}$ e as interferências no gráfico da função quando comparado à função original $f$.

• O parâmetro $a$ é responsável pelo deslocamento vertical do gráfico da função, de modo que a movimentação é feita para cima quando $a>0$ e para baixo se $a<0$. Veja o exemplo da Figura 3(a), em que o gráfico azul ilustra $g\left(x\right)=2+\mathrm{sen}\left(x\right)$ e o verde, $g\left(x\right)=-2+\mathrm{sen}\left(x\right)$.
• O parâmetro $b$ corresponde à alteração na amplitude do gráfico, podendo “encolher” o gráfico, se $\left|b\right|>1$ ou “esticar” o gráfico se $\left|a\right|<1$. Ainda, se $a<0$, ocorre uma reflexão do gráfico em relação ao eixo $x$. Observe a Figura 3(b), em que o gráfico azul ilustra $g\left(x\right)=2\mathrm{sen}\left(x\right)$, o verde representa $g\left(x\right)=\frac{1}{2}sen\left(x\right)$ e o roxo, $g\left(x\right)=-\mathrm{sen}\left(x\right)$.
• O parâmetro $c$ está associado ao período da função. Para $g\left(x\right)=\mathrm{sen}\left(cx\right)$ o período é dado por $p=\frac{2\pi }{c}$. Veja na Figura 3(c) o exemplo da função $g\left(x\right)=\mathrm{sen}\left(2x\right)$, indicado em azul, e o da função $g\left(x\right)=\mathrm{sen}\left(\frac{1}{2}x\right)$, descrito em verde.
• O parâmetro $d$ corresponde ao deslocamento horizontal da função. A curva é deslocada em $\frac{d}{c}$ unidades para a esquerda quando a razão foi positiva, e em  $\frac{d}{c}$unidades para a direita quando a razão for negativa. Observe a Figura 3(d), na qual estão indicadas as funções $g\left(x\right)=\mathrm{sen}\left(x+\pi \right)$ em azul e $g\left(x\right)=\mathrm{sen}\left(x-\frac{\pi }{3}\right)$ em verde.

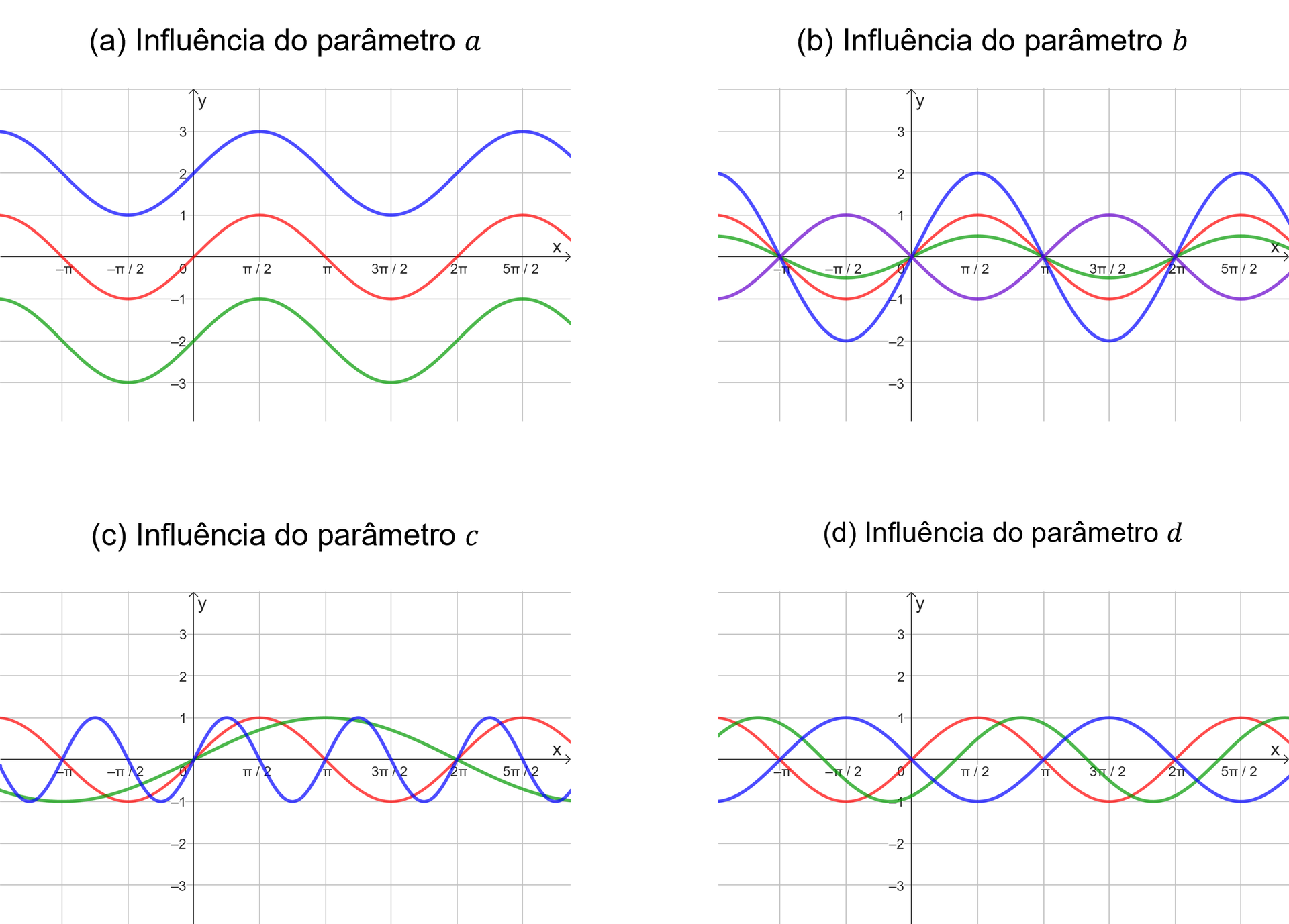
Figura 3 | Comparação entre as funções $f$ e $g$

Uma outra função que podemos definir é a tangente. A função tangente é definida por $h:D\to \mathrm{ℝ}$, tal que $h\left(x\right)=tg\left(x\right)$, em que o domínio é dado pelo conjunto $D=\left\{x\in \mathrm{ℝ};x\ne \frac{\pi }{2}+k\pi , \mathrm{com} k\in \mathrm{\mathbb{Z}}\right\}$. Note a necessidade de restrição do domínio, visto que a tangente não está definida para $x=90°=\frac{\pi }{2}$ e para $x=270°=\frac{3\pi }{2}$, bem como os ângulos correspondentes das demais voltas. O gráfico dessa função é apresentado na Figura 4. Comparando os gráficos das funções seno e cosseno com o da tangente percebemos várias diferenças, porém, os três representam funções periódicas, mas sendo a tangente de período $\pi$.

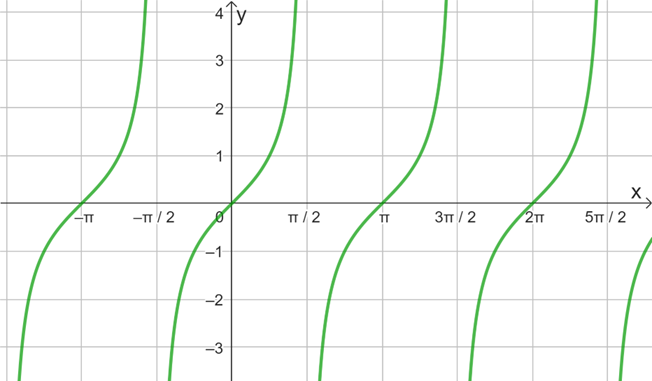
Figura 4 | Gráfico da função trigonométrica tangente

A aplicabilidade das funções trigonométricas seno, cosseno e tangente está vinculada a problemas que manifestam algum tipo de periodicidade, como é o caso das marés, cargas estruturais e superfícies em obras arquitetônicas, pressão sanguínea, a música e as ondas sonoras, entre outros.

Conhecendo as características básicas das funções trigonométricas, poderemos construir modelos a partir delas com o intuito de representar fenômenos reais e, por meio de sua interpretação, obter as soluções adequadas aos problemas reais associados. 

Vamos Exercitar?

Retornemos o problema do supermercado 24 horas. O modelo que foi construído para representar a quantidade de clientes em função do tempo é $C\left(x\right)=1000-700\cdot \mathrm{sen}\left(\frac{\pi \cdot x}{12}\right)$.

Queremos estudar os valores máximo e mínimo dessa função, para isso, precisamos investigar as características da função seno. Avaliando $f\left(x\right)=\mathrm{sen}\left(x\right)$, sabemos que ela tem seus valores variando no intervalo $\left[-\mathrm{1,1}\right]$, então -1 é o valor mínimo e 1 é o valor máximo da função. Sendo assim, $f$ admite o valor máximo 1 quando $x=90°=\frac{\pi }{2}$ rad ou qualquer ângulo das demais voltas que, no ciclo trigonométrico, coincidam com esse ângulo. Logo, o valor 1 é atingido para qualquer ângulo na forma $\frac{\pi }{2}+2\pi \cdot k$, com $k\in \mathrm{\mathbb{Z}}$. Por outro lado, o valor mínimo -1 é atingido para $x=270°=\frac{3\pi }{2}$ rad, ou em qualquer ângulo das demais voltas que coincidam com esse ponto. Logo, o valor -1 é atingido para $\frac{3\pi }{2}+2\pi \cdot n$, com $n\in \mathrm{\mathbb{Z}}$.

Considerando o valor máximo do seno, e tomando a função $C$, então podemos afirmar que o valor máximo de $C$ será atingido quando $\mathrm{sen}\left(\frac{\pi \cdot x}{12}\right)=-1$ porque, nesse caso, teremos $C\left(x\right)=1000-700\cdot \left(-1\right)=1000+700=1700$. Assim, devemos ter:

$\frac{\pi \cdot x}{12}=\frac{3\pi }{2}+2\pi \cdot n \Rightarrow \frac{x}{12}=\frac{3}{2}+2n \Rightarrow x=18+24n$

Como $x$ varia de 0 até 24, então admitindo $n=0$ teremos que a maior quantidade de clientes é verificada às 18:00. De modo análogo, o menor valor de $C$ será atingido quando $\mathrm{sen}\left(\frac{\pi \cdot x}{12}\right)=1$, pois teremos $C\left(x\right)=1000-700\cdot 1=1000-700=300$. Dessa forma,

$\frac{\pi \cdot x}{12}=\frac{\pi }{2}+2\pi \cdot k \Rightarrow \frac{x}{12}=\frac{1}{2}+2k \Rightarrow x=6+24k$

Como $x$ varia de 0 até 24, então admitindo $k=0$ teremos que a menor quantidade de clientes é verificada às 6:00. Observe na Figura 5 o gráfico para essa função, confirmando essas análises.

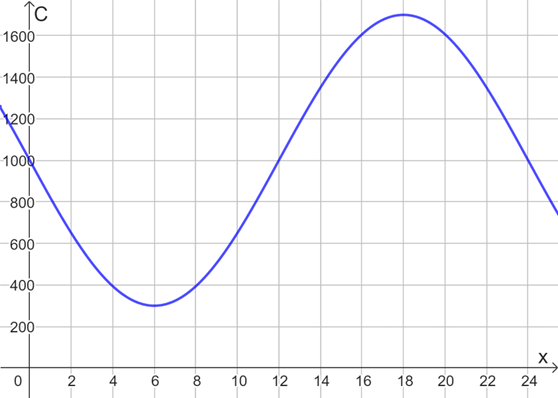
Figura 5 | Gráfico para a função $C\left(x\right)=1000-700\cdot \mathrm{sen}\left(\frac{\pi \cdot x}{12}\right)$

Com isso, concluímos a resolução desse problema, identificando que a quantidade máxima de clientes é 1700 e a mínima 300, sendo a variação no número de clientes dada por $1700-300=1400$. 

Saiba Mais

O livro Pré-Calculo, de Francisco M. Gomes, é uma sugestão interessante para o estudo dos gráficos de seno e cosseno, e gráficos das demais funções trigonométricas, apresentando de forma aprofundada suas características, em conjunto com exemplos. Para isso, estude as seções 6.4 Gráficos do seno e do cosseno e 6.5 Gráficos das demais funções trigonométricas, entre as páginas 478 e 494.

Como referência para o estudo das funções trigonométricas, sugerimos o livro Fundamentos de matemática para engenharias e tecnologias, de Giácomo A. Bonetto e Afrânio C. Murolo. Nas seções 8.5 Função seno, 8.6 Função cosseno e 8.7 Outras funções trigonométricas, no trecho entre as páginas 189 e 199, você terá acesso a um panorama geral sobre as funções trigonométricas, com exemplos.

Uma terceira sugestão é a obra Matemática com aplicações tecnológicas: matemática básica, de Seizen Yamashiro e Suzana A. de O. Souza. A partir da seção 10.7 Ciclo trigonométrico ou circunferência trigonométrica até o tópico 10.10.3 Domínio, conjunto imagem e período, entre as páginas 185 e 193, você poderá conferir algumas discussões acerca do ciclo trigonométrico e das características das funções trigonométricas.

 

 

Referências Bibliográficas

AXLER, S. Pré-cálculo: uma preparação para o cálculo com manual de soluções para o estudante. 2. ed. Rio de Janeiro: LTC, 2016.

BONETTO, G. A.; MUROLO, A. C. Fundamentos de matemática para engenharias e tecnologias. São Paulo: Cengage Learning Brasil, 2018.

GOMES, F. M. Pré-cálculo: operações, equações, funções e trigonometria. São Paulo: Cengage Learning Brasil, 2018.

STEWART, J.; CLEGG, D.; WATSON, S. Cálculo: Volume I. Tradução da 9. ed. norte-americana. São Paulo: Cengage Learning Brasil, 2021.

YAMASHIRO, S.; SOUZA, S. A. de O. Matemática com aplicações tecnológicas: matemática básica. Volume 1. São Paulo: Editora Blucher, 2014.

Videoaula de Encerramento

Olá, estudante! Nesta videoaula você retomará os conceitos envolvendo as funções, observando a definição formal e suas representações, além de aprofundar os estudos sobre funções afim, quadráticas, exponenciais, logarítmicas e trigonométricas.

Este conteúdo é importante para a sua prática profissional, pois o conceito de função, em conjunto com suas categoriais específicas, é um conhecimento indispensável à representação de problemas reais em linguagem matemática, por meio da modelagem matemática, o que propicia a resolução de problemas diversos.

Prepare-se para essa jornada de conhecimento!

Ponto de Chegada

A competência desta unidade consiste em compreender os principais aspectos relacionados a funções para resolver problemas em diferentes contextos. Para desenvolver essa competência você precisa, inicialmente, conhecer o conceito de função, o qual é a base para o estudo de qualquer categoria de função. É importante destacar que uma função precisa de três elementos para ser bem definida: domínio, contradomínio e lei de formação.

Em seguida, você deve compreender as características dos diferentes tipos de funções, reconhecendo-as e diferenciando-as entre si. Em relação às polinomiais, você deve compreender as características da função afim, cuja lei de formação assume o formato $f\left(x\right)=ax+b$ com $a$ e $b$ números reais, e da função quadrática, com lei de formação $f\left(x\right)=a{x}^2+bx+c$ sendo $a$, $b$ e $c$ números reais com $a$ diferente de zero. Para ambas as funções podemos estudar imagem, zeros, no entanto, enquanto a função afim tem uma característica linear, a função quadrática é descrita por uma parábola, podendo admitir um valor máximo ou mínimo.

Outras categorias importantes de funções são as exponenciais e logarítmicas, as quais estão relacionadas, respectivamente, às potências e aos logaritmos. Essas funções estão intimamente ligadas entre si, sendo inclusive inversas uma da outra, visto a relação existente entre as potências e os logaritmos por meio, entre outros, da própria definição de logaritmos. As funções exponenciais são relacionadas a fenômenos com crescimento ou decrescimentos rápidos, em comparação com as funções afim, enquanto na função logarítmica percebemos uma certa estabilidade a partir de certo ponto.

Por fim, com base nas razões trigonométricas, investigadas inicialmente a partir do triângulo retângulo, podemos definir as funções trigonométricas, com destaque para as funções seno, cosseno e tangente. Essas funções são do tipo periódicas, o que demonstra sua aplicabilidade em fenômenos que possuem essa natureza, como é o caso dos batimentos cardíacos, por exemplo. Nesse caso, é importante retomar a relação entre as medidas graus e radianos, tendo em vista a prevalência no uso dos radianos.

Nesse sentido, para desenvolver a competência, é importante que você estude os conceitos associados a cada categoria de função, refletindo sobre eles e reconhecendo os tipos de problemas que podem ser estudados com base nessas funções. 

Reflita Como é definida uma função? Quais são os principais tipos de funções e quais suas principais características? Em quais tipos de problemas podemos aplicar cada tipo de função?

É Hora de Praticar!

Estudante, tendo em vista a importância das funções para o estudo de diversos problemas reais, uma questão bastante importante consiste em avaliar diferentes fenômenos tendo em vista o reconhecimento da categoria de função mais adequada para sua representação. Nesse sentido, considere as situações descritas a seguir:

1. Durante uma partida de futebol, o goleiro chuta uma bola para enviá-la a um colega de equipe que está do outro lado do campo, de modo que a bola atinge um trajeto no formato parabólico. Qual foi a altura máxima atingida por essa bola durante esse trajeto?
2. Uma torneira foi aberta para esvaziar um reservatório, de modo que a vazão da água por essa torneira é constante. Qual o tempo necessário para esvaziar completamente esse reservatório, sabendo que a água está sendo retirada dele apenas por essa torneira?
3. A variação das marés em uma praia ao longo do dia ocorre periodicamente, de modo que a maré alta é de 3 metros, ocorrendo às 5h e às 11h, enquanto a maré baixa é de 1 metro e acontece às 14h e às 20h. Em quais instantes a maré atinge 2 metros?
4. Em uma cultura, a população de bactérias dobra a cada hora. Partindo de uma quantidade inicial de indivíduos, em quanto tempo a população de bactérias será oito vezes maior do que a quantidade inicial?

Para cada situação, faça um estudo acerca do tipo de função mais adequada para sua representação, evidenciando as características das funções que possibilitam esse tipo de associação.

Reflita

De que forma as propriedades da função escolhida contribuem para investigar o fenômeno apresentado?

Resolução do estudo de caso

Vamos fazer uma análise de cada situação apresentada, tendo em vista a categoria de função mais adequada para cada uma delas.

No contexto (a), envolvendo a partida de futebol, como o trajeto seguido pela bola é parabólico, então a função mais adequada é a quadrática, cujo gráfico tem o formato de uma parábola. Assim, pode ser construída, por exemplo, uma função $f\left(x\right)$ que expressa a altura da bola em função do tempo ou da distância do ponto inicial. O valor máximo pode ser associado ao vértice da função, considerando que a função do modelo deve ter seu coeficiente $a<0$, isto é, com concavidade voltada para baixo.

Em relação à situação (b), como a vazão é constante, podemos construir uma função afim $f\left(x\right)$ que associa o volume de água retirado do reservatório em função do tempo. Assim, é um fenômeno com característica linear e, por isso, pode ser associado a uma função polinomial de 1º grau.

Com relação à situação (c), a variação das marés em uma praia, sendo um fenômeno periódico, a função mais adequada é a trigonométrica, principalmente as do tipo seno e cosseno. Assim, para esse tipo de fenômeno, pode ser construída uma função do tipo $f\left(x\right)=a+b\mathrm{sen}\left(cx+d\right)$ ou $f\left(x\right)=a+b\cos \left(cx+d\right)$, com o ajuste dos parâmetros $a$, $b$, $c$ e $d$ conforme as propriedades do fenômeno.

Por fim, para o problema da população de bactérias do item (d), por se tratar de um fenômeno em que a quantidade dobra, ou se multiplica, a função mais adequada é a exponencial, visto que em problemas populacionais, em geral, tem crescimento exponencial. Assim, uma função na forma $f\left(x\right)=a\cdot b^{cx}$ pode ser ajustada para a representação e solução do problema em questão.

Dê o play!

Assimile

O conceito de função permeia diversos estudos feitos no campo da Matemática e nas áreas associadas. Assim, para contribuir com os estudos iniciais acerca das funções, estude o mapa mental apresentado no que segue, que engloba os conceitos iniciais sobre funções, bem como as características das principais categorias de funções. Complemente esse mapa incluindo expressões que auxiliam no estudo de cada categoria de função, como a fórmula do discriminante, por exemplo.

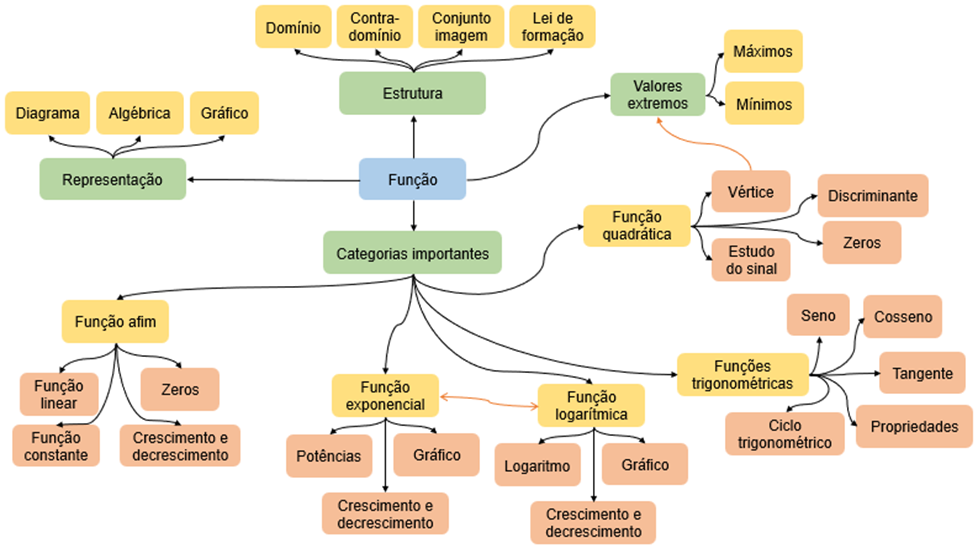
Referências

AXLER, S. Pré-cálculo: uma preparação para o cálculo com manual de soluções para o estudante. 2. ed. Rio de Janeiro: LTC, 2016.

BONETTO, G. A.; MUROLO, A. C. Fundamentos de matemática para engenharias e tecnologias. São Paulo: Cengage Learning Brasil, 2018.

GOMES, F. M. Pré-cálculo: operações, equações, funções e trigonometria. São Paulo: Cengage Learning Brasil, 2018.

SEIZEN, Y.; SOUZA, S. A. de O. Matemática com aplicações tecnológicas: matemática básica. v. 1. São Paulo: Editora Blucher, 2014.

STEWART, J.; CLEGG, D.; WATSON, S. Cálculo: Volume I. Tradução da 9. Ed. norte-americana. São Paulo: Cengage Learning Brasil, 2021.