Juros e Parcelamentos - Conceitos Básicos

Juros simples e taxa equivalente

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula. 

Ponto de Partida

Olá, estudante!
Nesta aula, você conhecerá alguns conceitos iniciais da Matemática Financeira como: juros simples, taxa equivalente e montante, os quais podem ser encontrados em nosso dia a dia em diversas situações, como cálculo de juros em um empréstimo ou na compra de um eletrodoméstico, aplicação de taxas, entre outros.
Para melhor compreender sobre o assunto, considere a situação do Davi, que precisa comprar alguns itens para seu escritório e a loja oferece a seguinte condição de pagamento: compras com entrada de 25% do valor à vista e pagamento até 10 dias, sob taxa de juros simples de 2,7% a.m.
Como Davi realizou uma compra de R$ 800,00, quanto ele irá pagar no prazo final? Se você estivesse no lugar do Davi, como faria para resolver essa situação? Para isso, vamos dar início ao nosso estudo!

Vamos Começar!

Juros simples

O conceito de juros simples pode ser aplicado em situações do nosso dia a dia, como cálculo em multas, cheque especial, impostos, entre outros.
De acordo com Moreira (2010), o conceito de juros surgiu há muito tempo quando o homem relacionou o tempo com ganho de dinheiro, com processos de acumulação de capital e a desvalorização da moeda. Na Matemática Financeira, para aprofundarmos sobre o cálculo dos juros, primeiramente precisamos conhecer a definição de alguns termos:

• Taxa de juros (i): é a unidade de medida dos juros, correspondente à remuneração paga pelo uso, durante determinado tempo, apresentada nas situações pela porcentagem.
• Por exemplo: um empréstimo com taxa de 2% ao mês:

$2\%=\frac{2}{100}=\mathrm{0,02}$

Tal que, 2% referem-se à taxa percentual e 0,02 à taxa unitária. Uma observação importante é que o mercado financeiro trabalha com base na taxa de juros percentual, porém é necessário colocá-la na forma unitária para realizar os cálculos financeiros. 

• Tempo (n): prazo da operação financeira, o qual deve estar equivalente ao período da taxa. 
• Capital (C): quantidade de recurso financeiro disponível ou exigido no ato de uma operação financeira, compra ou aplicação. O capital também é denominado valor presente (VP) e valor atual (VA).
• Juros (J): é a remuneração do capital empregado, ou seja, se aplicarmos um determinado valor durante um período de tempo, ao fim do prazo, obteremos um valor de juros. 
• Montante (M): também denominado como valor futuro (VF), é o resultado futuro de operações financeiras realizadas com o capital.

O juro simples é calculado sempre sobre o valor do capital inicial. Os juros de cada período são obtidos multiplicando a taxa de juros (i) pelo capital (C) e pelo tempo da aplicação (n), dado pela seguinte fórmula:

$J=C.i.n$

Para melhor compreender, observe o exemplo:
Joana emprestou R$ 1500,00 de uma instituição bancária para pagar daqui 4 meses, com uma taxa de 2% a.m. no regime de juros simples. Quanto Joana pagará de juros para instituição bancária?
Temos que:

$C=1500$

$n=4 meses$

$i=2\% a.m= \frac{2}{100}=\mathrm{0,02}$

Substituindo na fórmula:

$J=C.i.n$

$J=\mathrm{1500.0,02.4}$

$J=\mathrm{120,00}$

Montante

Com intuito de aprofundar ainda mais sobre o regime de capitalização de juros simples, vamos abordar o cálculo do montante. 
O montante também é conhecido como valor futuro e na língua inglesa, usa-se Future Value, indicado nas calculadoras financeiras pela tecla FV. O cálculo do montante é a soma do capital com os juros, ou seja, a partir da seguinte fórmula:

$M=C(1+i.n)$

Observe um exemplo do cálculo do montante:
Marcos investiu R$ 10.500,00 a uma taxa simples de 12% a.a., quanto ele terá ao final de 12 meses?
Temos que o capital é:

$C=10.500$

O período é $n=12 meses$.

 

E a taxa que está ao ano deverá ser convertida ao mês, para que se torne equivalente ao período da taxa, logo:

$i=12\% a.a=1\% a.m \frac{1}{100}=\mathrm{0,01}$

Agora, deve-se substituir na fórmula: 

$M=C(1+i.n)$

$M=10 500(1+\mathrm{0,01.12})$

$M=10 500(1+\mathrm{0,12})$

$M=10 500\left(\mathrm{1,12}\right)$

$M=11 760$

Logo, o montante será R$ 11 760,00.

Siga em Frente...

Taxa equivalente

Para que possamos compreender sobre taxa equivalente, primeiramente, vamos abordar sobre o período comercial, qual é utilizado em transações financeiras:

• 1 mês = 30 dias
• 1 ano = 12 meses 
• 1 ano = 360 dias

Essas informações serão necessárias para toda nossa disciplina, pois antes de calcular qualquer fórmula você deve se atentar se o período temporal da taxa de juros (i) e período (n) estão equivalentes, ou seja, se a taxa de juros (i) está ao ano, o período (n) também deve estar ao ano. 
Se por acaso esses períodos temporais estiverem diferentes, faz-se necessário o cálculo da taxa equivalente. No regime de capitalização do juros simples a taxa equivalente i_eq é calculada da seguinte forma: quando a taxa for apresentada numa referência maior que a solicitada, deverá dividir pela proporção da referência. Quando a taxa for apresentada numa referência menor que a solicitada, deverá multiplicar pela proporção da referência menor. 
Por exemplo: Carmem emprestou um valor X de seu irmão comprometendo-se a pagar após 4 meses, com uma taxa de 15% a.a. no regime de juros simples. A taxa está equivalente com o período? Como podemos deixá-la equivalente?
Observe que a taxa de juros está ao ano e o período de tempo está ao mês, logo, faz-se necessário deixar a taxa equivalente. Para isso, como temos a taxa ao ano, um período de referência maior que o período ao mês, vamos dividir a taxa por 12. 

$i=15\% a.a= i_{eq}=\frac{15\%}{12}=\mathrm{1,25}\%a.m$

Logo, a taxa equivalente será $i_{e}q=1,25\%a.m.$

Vamos Exercitar?

Para colocar em prática os conceitos vistos, considere a situação Davi, que precisa comprar alguns itens para seu escritório e a loja oferece a seguinte condição de pagamento:

• Compras com entrada de 25% do valor à vista e pagamento até 10 dias, sob taxa de juros simples de 2,7% a.m.

Como Davi realizou uma compra de R$ 800,00, quanto ele irá pagar no prazo final? Se você estivesse no lugar do Davi, como faria para resolver essa situação? Primeiramente, temos que calcular o valor da entrada, ou seja, 25% de 800:

$25\% de 800=\frac{25}{100}.800=\frac{20000}{100}=200$

Como a entrada é R$ 200,00, subtraindo do valor da compra de R$ 800,00, temos que o capital é:

$C=600$$M=C(1+i.n)$

O período é $n=10 dias.$

E a taxa que está ao mês deverá ser convertida ao dia, para que se torne equivalente ao período da taxa, logo:

$i_{eq}=\mathrm{2,7}\% a.m= \frac{\mathrm{2,7}\%}{30 dias}=\mathrm{0,09}\% a.d= \frac{\mathrm{0,09}}{100}=\mathrm{0,0009}$

Agora, deve-se substituir na fórmula:

$M=C(1+i.n)$

$M=600(1+\mathrm{0,0009.10})$

$M=600(1+\mathrm{0,009})$

$M=600\left(\mathrm{1,009}\right)$

$M=\mathrm{605,40}$

Logo, João pagará no prazo final R$ 605,40.

Saiba Mais

Para saber mais sobre o regime de capitalização de juros simples leia o artigo Uma breve introdução à matemática financeira: juros simples de José Bonifácio de Araújo Júnior.

Referências Bibliográficas

ARAÚJO JÚNIOR, J. B. Uma breve introdução à matemática financeira: juros simples. Revista Processus Multidisciplinar, v. 1, n. 1, p. 29-38, 2020.
CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.
MOREIRA, F. R. et al. Juros: conceitos e aplicações. Enciclopédia Biosfera, v. 6, n. 9, 2010.

Séries de juros simples

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você vai aprofundar ainda mais seus estudos com relação ao regime de capitalização de juros simples, desde fazer uma discussão sobre empréstimos, os juros simples e o parcelamento e, por fim, compreender como calcular prestações em situações que envolvem os juros simples com e sem entrada.  
Para colocar em prática o cálculo de parcelamento com juros simples, considere a situação da Ana, que para compra de uma máquina nova para sua empresa, parcelou em 3 vezes mensais uma quantia de R$ 4.500,00 com taxa de juros simples de 5% a.m. Determine o valor de cada parcela que Ana vai pagar. 
Antes de resolver o problema da Ana, vamos realizar um estudo sobre parcelamento!

Vamos Começar!

Parcelamento

Muitas vezes, você, ao comprar um móvel, imóvel ou qualquer outra coisa financiada, precisa calcular o valor das parcelas a serem pagas. Você já viu o seguinte tipo de anúncio: Taxa de juros de 0,89%! Saberia verificar se o valor da parcela pago pelo produto foi calculado exatamente com essa taxa de juros? 
Para isso, vamos aprender o conceito de séries, que utilizamos em situações que envolvem parcelamento e prestações. Essa fórmula das séries deve ser aplicada em problemas que envolvam poucas parcelas. 

As séries de juros simples são compostas a partir da equação geral do montante de juros simples, da seguinte forma:

$M=C(1+i.n)$

$C=\frac{M}{(1+i.n)}$

Considerando que cada parcela ou prestação são pequenos montantes (M) e o valor à vista de uma compra é o capital, temos:

$C_1=M_1/(1+i.n_1)"";C_2=\frac{M_2}{\left(1+i.n_2\right)};\dots ;C_j=\frac{M_j}{\left(1+i.n_j\right)}$

Logo,

$C=C_1+C_2+\dots +C_j$

Tal que:

$C=\frac{M_1}{(1+i.n_1)}+\frac{M_2}{(1+i.n_2)}+\dots +\frac{M_j}{(1+i.n_j)}$

Então:

$C={\sum }_{j=1}^j\frac{M_j}{(1+i.n_j)}$

Tal que,

• C: capital
• M: montante (parcelas)
• i: taxa de juros
• n: período de cada parcela

Siga em Frente...

Juros simples no parcelamento

Quando pretendemos trabalhar com parcelamento no regime de capitalização de juros simples, deve-se utilizar a fórmula de série:

$C={\sum }_{j=1}^j\frac{M_j}{(1+i.n_j)}$

Tal que C refere-se ao capital, M é o resultado do montante (parcelas), i o valor da taxa de juros, n o período de cada parcela. Para melhor compreender, observe o exemplo a seguir: 
João pretende comprar uma televisão em 2 vezes mensais e iguais, tal que o preço à vista é R$ 740,00. Se o parcelamento será realizado sob a taxa de juros simples de 4% a.m., qual o valor das parcelas?
Neste caso, temos 2 vezes iguais e mensais, ou seja, 2 parcelas iguais a M (Cada uma delas vale M). Como são mensais, ocorrerão nos meses 1 e 2 a partir da compra e o valor à vista que equivale ao capital (C) é igual a R$ 740,00.
A taxa de juros simples é igual a i = 4% a.m. Lembre-se que, conforme vimos na seção anterior, temos que transformar a taxa percentual para unitária, ou seja, i = 0,04 a.m.

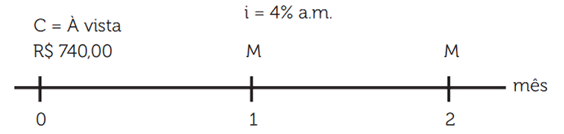
Aplicando a equação da série de juros simples:

$C={\sum }_{j=1}^j\frac{M_j}{(1+i.n_j)}$

$\frac{M}{1+\mathrm{0,04}\bullet 1}+\frac{M}{1+\mathrm{0,04}\bullet 2}=740$

 

Vamos colocar o M em evidência,

$\left(\frac{1}{\mathrm{1,04}}+\frac{1}{\mathrm{1,08}}\right)M=740$

$\left(\mathrm{0,9615}+\mathrm{0,9259}\right)\mathrm{M}=740$

$\mathrm{1,8874}M=740$

$M=\frac{740}{\mathrm{1,8874}}=\mathrm{392,07}$

Portanto, serão duas parcelas mensais e iguais a R$ 392,07.

Séries de juros simples

Utilizamos a série de juros simples em situações que necessitam do cálculo de prestações e parcelamentos, em tal regime de capitalização. Agora, vamos continuar abordando este tema, porém quando temos o pagamento de uma entrada, na seguinte fórmula: 

$AV-E={\sum }_{j=1}^j\frac{M_j}{(1+i.n_j)}$

Tal que,

• AV: valor à vista
• M: montante (parcelas)
• i: taxa de juros
• n: período de cada parcela
• E: valor da entrada

Observe um exemplo:
Uma impressora está em promoção com duas parcelas iguais a R$ 400,00, vencendo em dois meses, com entrada de R$ 200,00. Sabendo que esses valores foram obtidos sob taxa de juros simples de 60% a.a., determine o valor à vista da impressora.

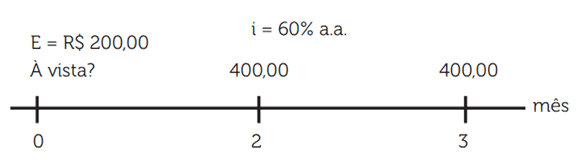
Primeiramente, temos que deixar nossa taxa equivalente, uma vez que está ao ano e precisamos passar para ao mês.

$i_{eq}=\frac{60\%}{12}=5\% a.m$

Na sequência, é preciso substituir os valores na fórmula da série de juros simples com entrada.

$AV-E={\sum }_{j=1}^j\frac{M_j}{(1+i.n_j)}$

$AV-200=\frac{400}{1+\mathrm{0,0}·2}+\frac{400}{1+\mathrm{0,05}·3}$

$AV=\frac{400}{\mathrm{1,1}}+\frac{400}{\mathrm{1,15}}+200$

$AV=\mathrm{363,64}+\mathrm{347,83}+200$

$AV=\mathrm{911,47}$

Portanto, o valor à vista da impressora é R$ 911,47.

Vamos Exercitar?

Para colocar em prática os conceitos vistos, considere a situação da Ana, que parcelou em 3 vezes mensais uma quantia de R$ 4.500,00, com taxa de juros simples de 5% a.m., para compra de uma máquina nova para sua empresa. Determine o valor de cada parcela que Ana vai pagar. 

$C=\sum _{j=1}^j\frac{M_j}{1+i{n}_j}$

$4500=\frac{M}{1+\mathrm{0,05}·1}+\frac{M}{1+\mathrm{0,05}·2}+\frac{M}{1+\mathrm{0,05}·3}$

Logo, Ana pagará R$ 1.647,69 em cada parcela. 

Saiba Mais

Para saber mais sobre parcelamento e séries de juros simples, leia o artigo Sistema de prestações constantes no regime de juros simples de Clovis de Faro e Gerson Lachtermacher.

Referências Bibliográficas

CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.
FARO, C.; LACHTERMACHER, G. Sistema de prestações constantes no regime de juros simples. Revista Estudos e Negócios Academics, v. 3, n. 5, p. 3-13, 2023.
MOREIRA, F. R. et al. Juros: conceitos e aplicações. Enciclopédia Biosfera, v. 6, n. 9, 2010.
 

Juros compostos e taxa equivalente

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você vai conhecer o regime de capitalização de juros compostos, que difere do regime de capitalização de juros simples, pois considera o resgate dos juros a cada período. Os juros são calculados sobre o valor corrigido do período anterior e a taxa de juros varia exponencialmente em função do tempo. 
Para colocar em prática o cálculo do montante dos juros compostos, considere a situação da Alana que comprou um aparelho celular no valor de R$ 900,00 e irá pagá-lo no prazo de 2 meses, a partir da seguinte condição de pagamento:

• Compras com pagamento entre 30 e 60 dias, sem entrada, sob taxa de juros compostos de 42,58% a.a.

Diante disso, quanto Alana pagará no aparelho celular no final dos 2 meses? Antes de resolver essa situação, vamos abordar os conceitos relacionados ao regime de capitalização de juros compostos, desde cálculo do montante e taxa equivalente. 

Vamos Começar!

Juros compostos

O juro composto é calculado sobre o montante relativo ao período anterior, em que os juros são incorporados, a cada período de capitalização, ao principal. Para seu cálculo também utilizaremos as seguintes nomenclaturas:

• Capital (C): quantidade de recurso financeiro disponível ou exigido no ato de uma operação financeira, compra ou aplicação. O capital também é denominado como valor presente (VP) e valor atual (VA).
• Montante (M): também denominado como valor futuro (VF), é o resultado futuro de operações financeiras realizadas com o capital.
• Juros (J): são as compensações financeiras nas operações realizadas, representando um acréscimo.
• Taxa (i): taxa de juros aplicadas sobre o capital (C).
• Período (prazo) (n): período de tempo da incidência da taxa de juros sobre o capital (C).

Os juros compostos são bem mais utilizados que juros simples em nosso dia a dia, especialmente em aplicações, investimentos, empréstimos, cálculos de prestações, financiamentos, entre outros.
Geralmente, nas mais diversas situações, temos que considerar o prazo n de acordo com a unidade de tempo da taxa, ou vice-versa, o que se faz necessário calcular as taxas equivalentes para diferentes períodos.

Montante

Quando pretendemos trabalhar com cálculo do montante, o resultado futuro de operações financeiras realizadas com o capital, no regime de capitalização de juros compostos, é calculado por meio da fórmula do montante:

$M=C.{\left(1+i\right)}^n$

Em que: 

• M: montante ou valor futuro
• C: capital ou valor presente
• i: taxa de juros
• n: período de tempo ou prazo da operação financeira

Observe o exemplo a seguir para melhor compreender o cálculo do montante para regime de capitalização de juros compostos. 
Sonia emprestou R$ 1.000,00 de uma instituição bancária a uma taxa de juros compostos de 4% a.m. (ao mês), para pagar após dois meses. Determine o valor que ela pagará no final para instituição bancária. 

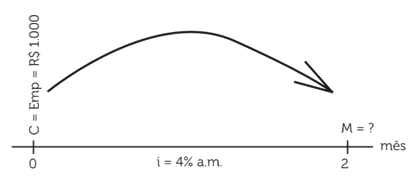
Substituindo os valores na fórmula do montante,

$M=C{\left(1+i\right)}^n$

$M=1000{\left(1+\mathrm{0,04}\right)}^2$

$M=1000·\mathrm{1,04}²$

$M=1000·\mathrm{1,0816}$

$M=1\mathrm{ }\mathrm{081,60}$

Siga em Frente...

Taxa equivalente

As taxas equivalentes são as taxas de juros fornecidas em unidades de tempo diferentes do prazo da operação financeira, ou vice-versa. Quando estas são aplicadas a um mesmo principal durante um mesmo prazo, produzem um mesmo montante acumulado, no regime de juros compostos. Para isso, no período comercial, sempre devemos considerar o seguinte:

• 1 ano = 6 bimestres
• 1 ano = 4 trimestres
• 1 ano = 3 quadrimestres
• 1 ano = 2 semestres
• 1 biênio = 2 anos 
• 1 triênio = 3 anos

Para o cálculo da taxa equivalente no regime de capitalização dos juros compostos, considere a seguinte fórmula:

$i_{eq}={\left(1+i\right)}^{\frac{p}{a}}-1$

Em que (a) é o período apresentado e (p) é o período pedido ou desejado.
Vejamos um exemplo para melhor compreensão: 
Lucas emprestou um valor X para seu irmão a uma taxa de juros compostos de 14% a.a. para pagar em 12 meses. 
Nesta situação, a taxa de juros está ao ano e o prazo da operação financeira está ao mês, logo, faz-se necessário deixar as taxas equivalentes. Para isso, primeiramente, temos que calcular com a menor unidade, ou seja, o mês.
A fórmula a ser utilizada será a de taxa equivalente para juros compostos:

$i_{eq}={\left(1+i\right)}^{\frac{p}{a}}-1$

$i_{eq}={\left(1+\mathrm{0,14}\right)}^{1/12}-1$

$i_{eq}={\left(\mathrm{1,14}\right)}^{1/12}-1$

$i_{eq}={\left(\mathrm{1,14}\right)}^{\mathrm{0,0833}}-1$

$i_{eq}=\mathrm{1,011}-1$

$i_{eq}=\mathrm{0,011}\mathrm{ }a.m$

$i_{eq}=\mathrm{1,1}\% a.m$

Logo, a taxa equivalente a 14% a.a. ao mês será i = 1,1% a.m.

Vamos Exercitar?

Para colocar em prática os conceitos vistos, considere a situação da Alana que comprou um aparelho celular no valor de R$ 900,00 e irá pagar no prazo de 2 meses, a partir da seguinte condição de pagamento:

• Compras com pagamento entre 30 e 60 dias, sem entrada, sob taxa de juros compostos de 42,58% a.a.

Diante disso, quanto Alana pagará no aparelho celular no final dos 2 meses?

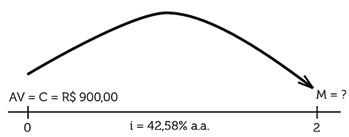
Considerando as informações extraídas do problema, antes de calcularmos o montante, devemos deixar a taxa i = 42,58% a.a. equivalente ao mês. Para isso, vamos utilizar a fórmula de taxa equivalente de juros compostos:

$i_{eq}={\left(1+i\right)}^{\frac{p}{a}}-1$

Em que, 

• i = 42,58% a.a. = 0,4258 a.a.
• a = 12; pois a taxa apresentada é ao ano e 1 ano é igual a 12 meses.
• p = 1; pois a taxa pedida é ao mês, ou em um mês.

Substituindo os valores na fórmula, temos:

$i_{eq}={\left(1+i\right)}^{p/a}-1$

$i_{eq}={\left(1+\mathrm{0,4258}\right)}^{1/12}-1$

$i_{eq}={\left(\mathrm{1,4258}\right)}^{1/12}-1$

$i_{eq}={\left(\mathrm{1,4258}\right)}^{\mathrm{0,0833}}-1$

$i_{eq}=\mathrm{1,0300}-1$

$i_{eq}=\mathrm{0,0300}\mathrm{ }a.m$

$i_{eq}=3\% a.m$

Sendo assim, a taxa utilizada será i = 3% a.m., ou seja, i = 0,03 a.m. Substituindo os valores na fórmula do montante:

$M=C{\left(1+i\right)}^n$

$M=900{\left(1+\mathrm{0,03}\right)}^2$

$M=900·\mathrm{1,0609}$

$M=R\mathrm{\$}\mathrm{954,81}$

Portanto, o valor a ser pago após 2 meses por Alana será de R$ 954,81.

Saiba Mais

Para saber mais sobre o regime de capitalização dos juros compostos leia o artigo Sistema de Juros Compostos de Wilson de Oliveira. 

Referências Bibliográficas

CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.
MOREIRA, F. R. et al. Juros: conceitos e aplicações. Enciclopédia Biosfera, v. 6, n. 9, 2010.
OLIVEIRA, W. Sistema de juros compostos. Revista Processus Multidisciplinar, v. 1, n. 1, p. 11-22, 2020.

Série de juros compostos

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Nesta aula, você vai aprofundar ainda mais seus estudos com relação ao regime de capitalização de juros compostos, desde fazer uma discussão sobre empréstimos, os juros simples e o parcelamento e, por fim, compreender como calcular prestações em situações que envolvem os juros compostos com e sem entrada.  
Para colocar em prática o cálculo de parcelamento com juros compostos, considere a condição de pagamento da loja MM:

• Compras parceladas em até 6 vezes com taxa de juros compostos de 56% a.a.

Neste sentido, qual valor da compra realizada pela Melissa, sabendo que vai pagar três parcelas mensais de R$ 500,00? Vamos lá!
 

M=7401,8861=392,34Vamos Começar!

Parcelamento

Com os juros simples, para o cálculo de parcelamento em juros compostos também vamos utilizar as séries. Em situações que envolvem parcelamento, prestações em pequenas quantidades, vamos utilizar a fórmula das séries. Para cálculos com quantidades maiores de parcelas faz-se uso da fórmula do valor presente, o qual veremos mais adiante em nosso livro. 

$M=C{.(1+i)}^n$

$C=\frac{M}{{\left(1+i\right)}^n}$

Considerando que cada parcela ou prestação são pequenos montantes (M) e o valor à vista de uma compra é o capital, temos:

$C_1=\frac{M_1}{{\left(1+i\right)}^{n_1}};C_2=\frac{M_2}{{\left(1+i\right)}^{n_2}};\dots ;C_j=\frac{M_j}{{\left(1+i\right)}^{n_j}}$

Logo,

$C=C_1+C_2+\dots +C_j$

Tal que:

$C=\frac{M_1}{{(1+i)}^{n_1}}+\frac{M_2}{{(1+i)}^{n_2}}+\dots +\frac{M_j}{{(1+i)}^{n_j}}$

Então:

$C={\sum }_{j=1}^j\frac{M_j}{{\left(1+i\right)}^{n_j}}$

 

Tal que,

• C: capital
• M: montante (parcelas)
• i: taxa de juros
• n: período de cada parcela

Juros compostos no parcelamento

Conforme vimos na seção anterior, quando pretendemos trabalhar com parcelamento no regime de capitalização de juros compostos deve-se utilizar a fórmula de série:

$C={\sum }_{j=1}^j\frac{M_j}{{\left(1+i\right)}^{n_j}}$

Tal que C refere-se ao capital, M é o resultando do montante (parcelas), i o valor da taxa de juros, n o período de cada parcela. Para melhor compreender, observe o exemplo a seguir: 
Carla pretende comprar um equipamento eletrônico que custa R$ 740,00. Ela vai pagar em duas parcelas mensais e iguais. Sabendo que o parcelamento será realizado sob a taxa de juros compostos de 4% a.m., determine o valor das parcelas.
Neste caso, temos 2 vezes iguais e mensais, ou seja, 2 parcelas iguais a M (cada uma delas vale M). Como são mensais, ocorrerão nos meses 1 e 2 a partir da compra e o valor à vista que equivale ao capital (C) é igual a R$ 740,00.
A taxa de juro composto é igual a i = 4% a.m. Lembre-se, que conforme vimos na seção anterior, temos que transformar a taxa percentual para unitária, ou seja, i = 0,04 a.m.

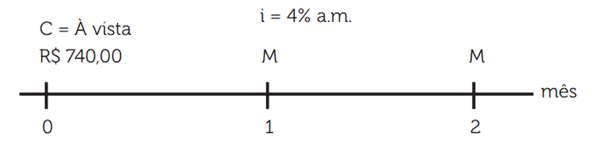
Aplicando a equação da série de juros compostos:

$C=\sum _{j=1}^j\frac{M}{{\left(1+i\right)}^n}$

$740=\frac{M}{{\left(1+\mathrm{0,04}\right)}^1}+\frac{M}{{\left(1+\mathrm{0,04}\right)}^2}$

$740=\frac{M}{{\left(\mathrm{1,04}\right)}^1}+\frac{M}{{\left(\mathrm{1,04}\right)}^2}$

 

Vamos colocar o M em evidência,

$\left(\frac{1}{\mathrm{1,04}}+\frac{1}{\mathrm{1,0816}}\right)M=740$

$\left(\mathrm{0,9615}+\mathrm{0,9246}\right)M=740$

$\mathrm{1,8861}M=740$

$M=\frac{740}{\mathrm{1,8861}}=\mathrm{392,34}$

Portanto, serão duas parcelas mensais e iguais a R$ 392,07.

Siga em Frente...

Séries de juros compostos

Agora, vamos continuar abordando este tema, porém quando temos o pagamento de uma entrada, na seguinte fórmula: 

$AV-E={\sum }_{j=1}^j\frac{M_j}{{\left(1+i\right)}^{n_j}}$

 

Tal que,

• AV: valor à vista
• M: montante (parcelas)
• i: taxa de juros
• n: período de cada parcela
• E: valor da entrada

Observe um exemplo:
Raquel comprou um móvel que custa R$ 900,00 e terá que pagar 25% do valor à vista de entrada e mais 2 parcelas iguais e mensais, sob taxa de juros compostos de 3,6% a.m. Qual valor de cada parcela?
Temos que,

• AV = R$ 900,00
• E = 25% de 900 = 225
• i = 3,6% a.m = 0,0360 a.m.

Substituindo os valores na fórmula da série de juros compostos com entrada, temos:

$AV-E={\sum }_{j=1}^j\frac{M_j}{{\left(1+i\right)}^{n_j}}$

$900-225=\frac{M}{{\left(1+\mathrm{0,0360}\right)}^1}+\frac{M}{{\left(1+\mathrm{0,0360}\right)}^2}$

$675=\frac{M}{\mathrm{1,0360}}+\frac{M}{\mathrm{1,0733}}$

 

Colocando o M em evidência,

$\left(\frac{1}{\mathrm{1,0360}}+\frac{1}{\mathrm{1,0733}}\right)M=675$

$\left(\mathrm{0,9653}+\mathrm{0,9317}\right)M=675$

$\mathrm{1,8970}M=675$

$M=\frac{675}{\mathrm{1,8970}}$

$M=R\$\mathrm{355,82}$

Portanto, Raquel pagará uma entrada de R$ 225,00 e mais duas parcelas de R$ 355,82.

Vamos Exercitar?

Para colocar em prática o cálculo de parcelamento com juros compostos, considere a condição de pagamento da loja MM:

• Compras parceladas em até 6 vezes com taxa de juros compostos de 56% a.a.

Neste sentido, qual valor da compra realizada pela Melissa, sabendo que vai pagar três parcelas mensais de R$ 500,00? Vamos lá!
Considerando as informações do problema, antes de calcularmos o valor da compra, devemos deixar a taxa i = 56% a.a. equivalente ao mês. Para isso, vamos utilizar a fórmula de taxa equivalente de juros compostos:

$i_{eq}={\left(1+i\right)}^{\frac{p}{a}}-1$

Em que, 

• i = 56% a.a. = 0,56 a.a.
• a = 12; pois a taxa apresentada é ao ano e 1 ano é igual a 12 meses.
• p = 1; pois a taxa pedida é ao mês, ou em um mês.

Substituindo,

$i_{eq}={\left(1+i\right)}^{\frac{p}{a}}-1$

$i_{eq}={\left(1+\mathrm{0,56}\right)}^{\frac{1}{12}}-1$

$i_{eq}={\left(\mathrm{1,56}\right)}^{\mathrm{0,0833}}-1$

$i_{eq}=\mathrm{1,0377}-1$

$i_{eq}=\mathrm{0,0377}$

$i_{eq}=\mathrm{3,77}\% a.m.$

 

Sendo assim, a taxa utilizada será i = 3,77% a.m., ou seja, i = 0,0377 a.m. Substituindo na fórmula das séries dos juros compostos, temos:

$C=\sum _{j=1}^j\frac{M}{{\left(1+i\right)}^n}$

$C=\frac{500}{{\left(1+\mathrm{0,0377}\right)}^1}+\frac{500}{{\left(1+\mathrm{0,0377}\right)}^2}+\frac{500}{{\left(1+\mathrm{0,0377}\right)}^3}$

$C=\frac{500}{{\left(\mathrm{1,0377}\right)}^1}+\frac{500}{{\left(\mathrm{1,0377}\right)}^2}+\frac{500}{{\left(\mathrm{1,0377}\right)}^3}$

$C=\frac{500}{\mathrm{1,0377}}+\frac{500}{\mathrm{1,0768}}+\frac{500}{\mathrm{1,1174}}$

$C=\mathrm{481,83}+\mathrm{464,34}+\mathrm{447,47}$

$C=\mathrm{1.393,64}$

Logo, o valor da compra foi de R$ 1.393,64.

Saiba Mais

Para saber mais sobre a série de juros compostos, leia o artigo Matemática financeira: juros compostos de José Bonifácio de Araújo Júnior.

Referências Bibliográficas

ARAÚJO JÚNIOR, J. B. Matemática financeira: juros compostos. Revista Processus Multidisciplinar, v. 1, n. 2, p. 46-51, 2020.
CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.
MOREIRA, F. R. et al. Juros: conceitos e aplicações. Enciclopédia Biosfera, v. 6, n. 9, 2010.
OLIVEIRA, W. Sistema de juros compostos. Revista Processus Multidisciplinar, v. 1, n. 1, p. 11-22, 2020.

Videoaula de Encerramento

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Chegada

Olá, estudante!
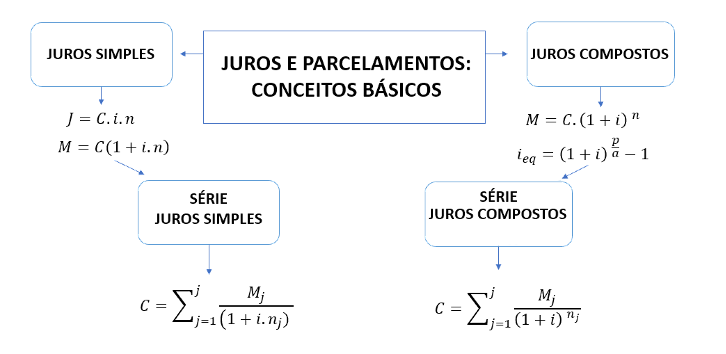
Para desenvolver a competência desta unidade, que é compreender os conceitos relacionados a juros e parcelamento para aplicá-los na resolução de problemas financeiros, é preciso diferenciar os regimes de capitalização de juros simples e compostos. 
Importante ressaltar que quando estamos nos referindo aos juros simples, estamos calculando os juros sempre sobre o valor do capital inicial, ou seja, eles são obtidos multiplicando a taxa de juros (i) pelo capital (C) e pelo tempo da aplicação (n), dado pela seguinte fórmula:

$J=C.i.n$

Além disso, devemos nos atentar para a taxa equivalente, em que o período temporal da taxa de juros (i) e período (n) devem estar equivalentes, ou seja, se a taxa de juros (i) está ao ano o período (n) também deve estar ao ano. 
Quando somamos o capital inicial ao juro aplicado encontramos o valor do montante, que nos juros simples pode ser calculado a partir da seguinte fórmula:

$M=C(1+i.n)$

Ainda no regime de capitalização dos juros simples, podemos calcular valores de prestações considerando algumas situações de financiamento, em que cada parcela ou prestação corresponde a pequenos montantes (M) e o valor à vista de uma compra é o capital, a partir da fórmula das séries:

$C={\sum }_{j=1}^j\frac{M_j}{(1+i.n_j)}$

Assim como nos juros simples, também temos diversos pontos a nos atentar sobre os juros compostos, pois estes são calculados sobre o valor corrigido do período anterior e a taxa de juros varia exponencialmente em função do tempo, ou seja, a taxa de juros é aplicada a cada período. 
Para o cálculo do montante (M) nos juros compostos, faz-se uso da seguinte fórmula:

$M=C.{\left(1+i\right)}^n$

Também deve-se atentar para as taxas equivalentes, pois o período de tempo da taxa de juros deve ser o mesmo do prazo da operação financeira, assim, utiliza-se a seguinte fórmula para o regime de capitalização de juros compostos:

$i_{eq}={\left(1+i\right)}^{\frac{p}{a}}-1$

Em que (a) é o período apresentado e (p) é o período pedido ou desejado.
Por fim, podemos calcular valor de prestações em financiamentos com uso da fórmula da série dos juros compostos, em que cada parcela ou prestação corresponde a pequenos montantes (M) e o valor à vista de uma compra é o capital.

$C={\sum }_{j=1}^j\frac{M_j}{{\left(1+i\right)}^{n_j}}$

Essa fórmula deve ser utilizada para situações com pequenas quantidades de parcelas, pois ao apresentar uma quantidade maior de parcelas faz-se uso da fórmula do valor presente, o qual será visto mais adiante na disciplina. 

 

É Hora de Praticar!

A loja de departamento disparou um panfleto promocional contendo a seguinte informação:

Sabendo que Mônica comprou um produto e vai pagar uma entrada de R$ 200,00 e mais duas parcelas iguais de R$ 400,00, vencendo em dois meses. Qual o valor à vista deste produto?

Reflita

Reflita sobre as perguntas a seguir:

• Você consegue identificar qual fórmula utilizar em cada situação-problema?
• Você extrai as informações de forma correta dos problemas?
• Você consegue identificar situações do seu dia a dia em nossa disciplina e como ela pode te ajudar?

 

Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Resolução do estudo de caso

Primeiramente vamos extrair as informações do problema:
E (entrada) = 200,00
M (2 parcelas) = 400,00
Vence em dois meses, então (n) começa em 2 meses. 
AV (valor a vista) = ?
i = 60% a.a. = 0,60 a.a
a = 12; pois a taxa apresentada é ao ano e 1 ano é igual a 12 meses.
p = 1; pois a taxa pedida é ao mês, ou em um mês.
Substituindo os valores na fórmula, temos:

$i_{eq}={\left(1+i\right)}^{p/a}-1$

$i_{eq}={\left(1+\mathrm{0,6}\right)}^{1/12}-1$

$i_{eq}={\mathrm{1,6}}^{\mathrm{0,0833}}-1$

$i_{eq}=\mathrm{1,0399}-1$

$i_{eq}=\mathrm{0,0399} a.m$

$i_{eq}=\mathrm{3,99}\% a.m$

Logo, temos que a taxa a ser utilizada será i = 3,99% a.m. Agora, vamos utilizar a fórmula das séries de juros compostos com entrada:

 

$AV-E={\sum }_{j=1}^j\frac{M_j}{{\left(1+i\right)}^{n_j}}$

 

Substituindo,

$AV-200=\frac{400}{{\left(1+\mathrm{0,0399}\right)}^2}+\frac{400}{{\left(1+\mathrm{0,0399}\right)}^3}$

$AV=\frac{400}{\mathrm{1,0814}}+\frac{400}{\mathrm{1,1245}}+200$

$AV=\mathrm{369,89}+\mathrm{355,71}+200$

$AV=\mathrm{925,60}$

Portanto, o valor do produto era R$ 925,60. 

Dê o play!

Assimile

Referências

CARVALHO, L. C. S.; ELIA, B. S.; DECOTELLI, C. A. Matemática financeira aplicada. Rio de Janeiro: FGV, 2009.
MOREIRA, F. R. et al. Juros: conceitos e aplicações. Enciclopédia Biosfera, v. 6, n. 9, 2010.
OLIVEIRA, W. Sistema de juros compostos. Revista Processus Multidisciplinar, v. 1, n. 1, p. 11-22, 2020.