Tabela Verdade

Fundamentos da tabela verdade

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Olá, estudante! Chegou um momento muito importante no qual aprenderemos os fundamentos da tabela verdade. O conhecimento sobre os fundamentos da tabela verdade fornecerão uma base sólida para analisar e avaliar a validade de argumentos lógicos, expressões booleanas e sistemas lógicos complexos. Eles permitem determinar de forma sistemática e objetiva os valores lógicos de expressões, ajudando a estabelecer a consistência e a coerência em raciocínios e tomadas de decisão, além de serem essenciais para a programação e para o design de circuitos lógicos em computação.

Suponhamos que estamos lidando com um sistema de controle de acesso a um escritório em que existem regras de segurança para permitir a entrada de funcionários.

Cenário:

A política de segurança do escritório exige que um funcionário seja permitido a entrar apenas se atender a uma das seguintes condições:

1. O funcionário tem um cartão de acesso válido (C).
2. O funcionário é um membro da equipe de segurança (S).
3. O funcionário é um gerente (M).

A pergunta é: "Sob que condições um funcionário deve ser permitido a entrar no escritório?"

Para vencer esse desafio, você aprenderá nesta seção os conteúdos referentes aos fundamentos da tabela verdade que irão te auxiliar no desenvolvimento de estudo de caso e torná-lo um grande desenvolvedor.

Vamos em frente!

Vamos Começar!

Definição

Uma tabela verdade, em lógica e matemática computacional, é uma representação tabular de todas as possíveis combinações de valores de entrada e as correspondentes saídas de uma expressão lógica ou função booleana. Essa tabela é usada para determinar o valor lógico de uma expressão em todas as situações possíveis, com base em suas variáveis de entrada.

A estrutura de uma tabela verdade é composta por colunas que representam as variáveis de entrada e uma coluna adicional que representa o resultado da expressão ou função booleana para cada combinação possível das variáveis de entrada.

Vamos considerar um exemplo simples. Suponha que tenhamos uma expressão lógica AND (E) com duas variáveis de entrada A e B. A Figura 1, ilustra uma tabela verdade para essa expressão:

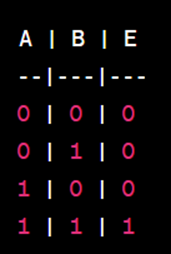
Neste exemplo, as colunas "A" e "B" representam as variáveis de entrada, enquanto a coluna "E" representa o resultado da operação AND entre A e B. A tabela verdade mostra todas as combinações possíveis de valores de A e B, bem como o resultado correspondente da operação AND.

A tabela verdade é frequentemente usada em várias aplicações, incluindo:

1. Análise de Expressões Lógicas: Ela é utilizada para avaliar o valor lógico de uma expressão lógica complexa em diferentes cenários. Isso é particularmente útil ao simplificar ou otimizar expressões lógicas.

2. Projeto de Circuitos Lógicos: Engenheiros e projetistas de hardware usam tabelas verdade para criar e testar circuitos digitais. Isso permite a verificação de como um circuito se comportará para todas as combinações possíveis de entrada.

3. Programação com Lógica Booleana: Em programação, a lógica booleana é comum em estruturas de controle, como condicionais e loops. Tabelas verdade são usadas para entender como as condições são avaliadas e as decisões são tomadas em um programa.

4. Tomada de Decisões Lógicas: Em sistemas de controle, automação e inteligência artificial, as tabelas verdade são usadas para modelar o comportamento lógico e tomar decisões com base nas entradas fornecidas.

As tabelas verdade são uma ferramenta fundamental em lógica e matemática computacional, ajudando a entender o comportamento de expressões lógicas e funções booleanas em diversas aplicações, como projeto de circuitos, programação e tomada de decisões baseadas em lógica.

Siga em Frente...

Tabela verdade com proposições intermediárias

Uma tabela verdade com proposições intermediárias, às vezes chamada de tabela de verdade estendida, é uma representação tabular de todas as possíveis combinações de valores de entrada e as correspondentes saídas de uma expressão lógica que inclui variáveis intermediárias ou proposições intermediárias. Essas proposições intermediárias são frequentemente usadas para representar etapas intermediárias de um cálculo ou para descrever o comportamento de sistemas lógicos mais complexos.

Uma definição mais ampla de tabela verdade com proposições intermediárias pode ser a seguinte:

Uma tabela verdade com proposições intermediárias é uma estrutura de dados tabular usada na lógica, matemática, ciência da computação e engenharia para analisar e representar o comportamento de expressões lógicas que envolvem variáveis de entrada, variáveis intermediárias e saídas lógicas. Essa tabela abrange todas as combinações possíveis de valores de entrada, bem como os valores intermediários, que são as etapas intermediárias do cálculo ou do sistema lógico, juntamente com os resultados finais.

Essas tabelas verdade estendidas são particularmente úteis ao lidar com sistemas lógicos complexos, em que o cálculo ou a representação do processo envolve etapas intermédias que são relevantes para a análise e tomada de decisões. Elas ajudam a compreender como as proposições intermediárias evoluem em resposta às variações das variáveis de entrada e como elas afetam a saída final.

Essas tabelas verdade, podem ser usadas em diversos contextos, como otimização de circuitos digitais, verificação de algoritmos complexos, modelagem de sistemas lógicos, entre outros. Elas fornecem uma visão abrangente e detalhada do comportamento de sistemas lógicos que envolvem múltiplas camadas de proposições e variáveis intermediárias.

Exemplo:

Suponha que tenhamos a seguinte expressão lógica que envolve proposições intermediárias:

• A, B e C são variáveis de entrada;
• X = A ˄ B
• Y = B ˅ C
• Z = X ˄ Y

Vamos criar uma tabela verdade estendida que abrange todas as combinações possíveis de valores de entrada e mostra os valores intermediários de X e Y junto com o resultado final que é Z.

Neste exemplo, as colunas "A", "B" e "C" representam as variáveis de entrada, as colunas "X" e "Y" representam as proposições intermediárias, e a coluna "Z" representa o resultado final. A tabela verdade estendida mostra como os valores intermediários são calculados e como eles afetam o resultado final Z.

Exercício:

Considere a seguinte expressão lógica com proposições intermediárias:

• P, Q, R são variáveis de entrada
• X = P ˄ Q
• Y=¬R
• Z = X ˅ Y

Crie uma tabela verdade estendida que abrange todas as combinações possíveis de valores de entrada e mostre os valores intermediários X e Y junto com o resultado final Z.

Neste exercício, conforme demonstrado na Figura 3, seguimos o mesmo procedimento que no exemplo anterior (Figura 2) para criar a tabela verdade estendida, levando em consideração as proposições intermediárias X e Y, e calculando o resultado final Z.

Tabela verdade para a Lei De Morgan

A tabela verdade para a Lei De Morgan é usada para demonstrar como as Leis De Morgan se aplicam a operações lógicas, especificamente a negação de conjunção (NAND) e a negação de disjunção (NOR). As Leis De Morgan estabelecem as relações entre negações e operações de conjunção e disjunção. Essas Leis são essenciais na simplificação de expressões lógicas e no projeto de circuitos digitais.

Exemplo

Vamos considerar a Lei De Morgan aplicada a uma expressão lógica com duas variáveis, A e B.

1.     A Lei de De Morgan para a negação de conjunção afirma que ¬(A ∧ B) = ¬A ∨ ¬B

2.     A Lei de De Morgan para a negação de disjunção afirma que ¬(A ∨ B)=¬A∧¬B.

Aqui está a tabela verdade que demonstra a primeira Lei de De Morgan (negação de conjunção):

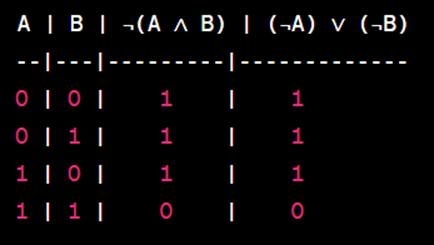
A Figura 4, ilustra a tabela verdade onde, as colunas "A" e "B" representam as variáveis de entrada, "¬(A ∧ B)" representa a negação da conjunção A∧B, e "(¬A) ∨ (¬B)" representa a disjunção das negações ¬A e ¬B. A tabela verdade demonstra que os valores são idênticos, confirmando a primeira Lei De Morgan.

Exercício:

Suponha que temos as variáveis P e Q e queremos demonstrar a segunda Lei De Morgan: ¬(P ∨ Q) = ¬P ∧ ¬Q. Crie uma tabela verdade que valide essa Lei.

Solução do Exercício:

A Figura 5, ilustra a tabela verdade que valida a segunda Lei De Morgan:

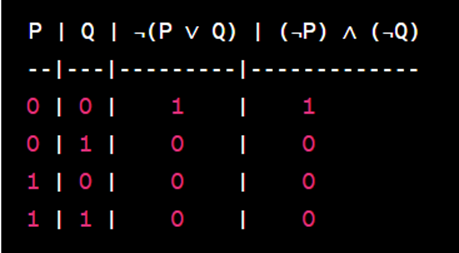
Nesta tabela verdade, as colunas "P" e "Q" representam as variáveis de entrada, "¬(P ∨ Q)" representa a negação da disjunção P∨Q, e "(¬P) ∧ (¬Q)" representa a conjunção das negações ¬P e ¬Q. A tabela verdade demonstra que os valores são idênticos, confirmando a segunda Lei de De Morgan.

Vamos Exercitar?

Chegou a hora de resolver seu desafio na qual estamos lidando com um sistema de controle de acesso a um escritório em que existem regras de segurança para permitir a entrada de funcionários.

Cenário:

A política de segurança do escritório exige que um funcionário seja permitido a entrar apenas se atender a uma das seguintes condições:

1.     O funcionário tem um cartão de acesso válido (C).

2.     O funcionário é um membro da equipe de segurança (S).

3.     O funcionário é um gerente (M).

A pergunta é: "Sob que condições um funcionário deve ser permitido a entrar no escritório?"

Expressão Inicial:

Podemos expressar essa política de segurança com a seguinte expressão lógica:

E= C ∨ S ∨ M

Aqui, usamos a operação de disjunção (∨) para indicar que o funcionário deve ser permitido a entrar se atender a pelo menos uma das condições.

Aplicação da Lei De Morgan:

Agora, aplicaremos a Lei De Morgan para negar a expressão, o que nos permitirá determinar quando o funcionário não deve ser permitido a entrar:

¬E = ¬(C∨S∨M)

Usaremos a primeira Lei De Morgan para a negação de uma disjunção:

¬E = ¬C ∧ ¬S ∧ ¬M

Aqui, usamos a operação de conjunção (∧) para indicar que o funcionário não deve ser permitido a entrar apenas se todas as condições não forem atendidas (ou seja, o funcionário não possui um cartão de acesso válido, não é membro da equipe de segurança e não é gerente).

Tabela Verdade:

Agora, vamos criar uma tabela verdade para as variáveis C, S, M e ¬E, demonstrando todas as combinações possíveis de estados das condições e se o funcionário deve ou não ser permitido a entrar.

A Figura 6, ilustra a tabela verdade, as colunas representam os estados das condições: cartão de acesso (C), equipe de segurança (S), gerente (M) e a negação da permissão de entrada (¬E). A negação da permissão de entrada é igual a 1 quando o funcionário não deve ser permitido a entrar e igual a 0 quando o funcionário deve ser permitido a entrar.

A tabela verdade ilustrada na Figura 6, mostra que o funcionário deve ser permitido a entrar (¬E = 0) apenas quando nenhuma das condições de segurança não for atendida, ou seja, quando o funcionário possui um cartão de acesso válido, é membro da equipe de segurança ou é gerente. Isso reflete a política de segurança do escritório: um funcionário deve ser permitido a entrar se atender a pelo menos uma das condições de segurança.

Este estudo de caso simulado ilustra como a Lei De Morgan pode ser aplicada em um cenário de controle de acesso a um escritório, juntamente com a criação de uma tabela verdade para determinar as condições sob as quais um funcionário deve ser permitido a entrar.

Saiba Mais

Fundamentos da tabela verdade são fundamentais para a compreensão da disciplina Lógica e Matemática Computacional. A seguir, algumas indicações para um estudo profundo sobre o tema.

1. BISPO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. Introdução à lógica matemática. Cengage Learning Brasil, 2017. O capítulo 2 deste livro aborda os tópicos referentes a: (1) Tabela Verdade, (2) Critérios para a tabela verdade e (3) Exercícios.
2. QUILELLI, P. Raciocínio lógico matemático para concursos. 3. Ed. Editora Saraiva, 2015. O capítulo 2 aborda os tópicos relacionados à tabela verdade e as regras da Lei De Morgan.

Referências Bibliográficas

BISPO FILHO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à lógica matemática. São Paulo: Cengage Learning, 2017.

FAJARDO, R. Lógica matemática. 1. ed. São Paulo: Edusp, 2017.

MUNDIM, R. P. A Lógica Formal – princípios elementares. Revista Economia & Gestão, Belo Horizonte, v. 2, n. 3, jan./jun. 2002.

SANTOS, M. da S. dos et al. Lógica computacional. Grupo A, 2021. 

Construção da tabela verdade

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Olá, estudante! Iniciaremos agora uma jornada que lhe capacitará compreender e aplicar a lógica por meio da construção de tabelas verdade. Quem tem irmão já deve ter ouvido a mãe gritar: “Você E seu irmão estão de castigo!”, mas esse “E” tem a ver com o conectivo lógico AND? A resposta é sim, o resultado desse E é o mesmo, seja na linguagem natural ou na binária, por isso aprendemos lógica proposicional e a aplicamos no universo computacional.

Você foi recentemente contratado como um funcionário trainee na área de analytics e almeja se tornar júnior em breve, mas para isso deve cumprir seus desafios e ajudar a equipe. Você recebeu uma planilha com os dados de compras de clientes, conforme ilustrado na Tabela 1. Dadas as seguintes proposições: p: o cliente é do sexo feminino, q: o cliente tem idade entre 20 e 30 anos, o seu desafio é construir uma Tabela Verdade que generalize a solução fazendo a conjunção e a disjunção para as proposições p e q, além de criar os resultados para a negação de ambas as fórmulas. Após criar a tabela verdade, você poderá analisar cada registro informando se o resultado é verdadeiro ou falso para cada um dos conectores lógicos propostos na Tabela 1. Tal resultado ajudará a equipe de vendas a criar rotinas para tomada de decisões.

codigo_cli	nome_cli	genero_cli	idade_cli	valor_compra	E	OU
53682	Karly Dillon	F	40	74,84	?	?
58246	Channing Vazquez	M	49	98,04	?	?
27022	Adria Key	F	47	65,93	?	?
82075	Ella Nelson	F	34	94,01	?	?
90657	Arden Battle	M	48	21,73	?	?
80330	Brittany Ramirez	F	38	42,23	?	?
53989	Moses Graham	M	42	37,20	?	?
61370	Jin Fuller	M	49	65,60	?	?
41807	Phelan Blair	M	46	77,40	?	?
94269	Porter West	M	22	67,19	?	?

Tabela 1 | Dados de compra dos clientes

 

Para cumprir seu desafio, nesta seção você aprenderá o mecanismo de construção de uma tabela verdade, bem como utilizar os conectores lógicos de conjunção, disjunção e negação. Então, mãos à obra!

Vamos Começar!

Provavelmente é do seu conhecimento que um computador é dividido em duas partes: o hardware (componentes físicos) e o software (os programas). Muitos pesquisadores contribuíram para que chegássemos ao nível de evolução computacional que vivenciamos. O avanço do hardware se deu por meio das pesquisas na área da eletrônica digital, que visa construir circuitos que representam grandezas por meio de valores discretos. Os componentes eletrônicos que compõem um computador são formados por pequenos elementos, chamados de transistores, que são capazes de lidar com dois estados, aberto ou fechado. Um conjunto de transistores pode ser usado para construir uma porta lógica, que ao receber sinais digitais de entrada produz uma determinada saída, que depende do tipo de operação lógica para o qual foi construído. Por exemplo, uma porta lógica pode receber um sinal de ligado (1) em uma entrada e um sinal de desligado (0) em outra, qual seria o resultado? Depende da operação lógica dessa porta; se for uma operação AND, o resultado seria “desligado”, mas se fosse um OR, o resultado seria “ligado”.

Assim como no hardware, o software também possui operações lógicas. Por exemplo, podemos escrever um programa que irá somar dois valores se, e somente se, ambos forem positivos. Nesse caso, teremos que construir o algoritmo utilizando o operador AND.

Construção da tabela verdade

Dada a necessidade de se obter resultados lógicos da combinação de proposições e conectores, um dos métodos mais utilizados é o método da tabela verdade.

Por definição, a tabela verdade é um método exaustivo de geração de valorações para uma dada fórmula. Entendemos por fórmula a composição de proposições e conectores lógicos por exemplo, P ˅ Q. Observe o esquema geral da tabela verdade na Figura 1. Nas colunas, colocaremos primeiro as proposições (quantas forem necessárias testar) e, em seguida, as operações lógicas das quais queremos obter os resultados. Já nas linhas, colocaremos os valores lógicos (V – F) tanto para as proposições quanto para os resultados das fórmulas que obteremos, lembrando que nosso objetivo com a tabela verdade é analisar TODOS os resultados possíveis, e podemos compará-la com um mapa de resultados.

Obtida a tabela uma vez, basta consultá-la.

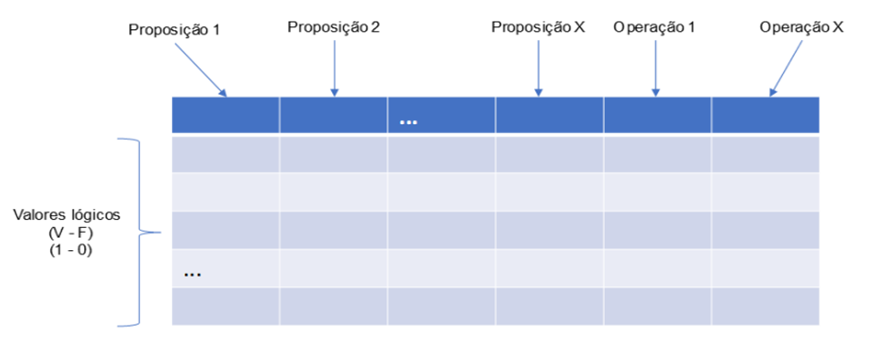
Alguns pontos sobre a lógica têm que estar bem claros para que possamos construir nossas tabelas verdade.

Toda proposição é binária, ou seja, só pode assumir um dos seguintes valores: verdadeiro (V) ou falso (F). Você pode optar por utilizar 1 para V e 0 para F.

Ao realizar uma operação lógica com duas proposições, temos que testar todas as combinações de respostas, o que influenciará diretamente a quantidade de linhas necessárias na tabela verdade.

Siga em Frente...

Tabela verdade de conjunção (and – e)

O conector lógico de conjunção (AND - E) é utilizado para realizar uma operação binária entre duas proposições, quando se deseja obter um resultado verdadeiro se, e somente se, as duas proposições forem verdadeiras. Utilizaremos o símbolo ʌ para representar esse conector lógico. Para construir a tabela verdade da conjunção, vamos considerar como entradas as proposições A e B. Queremos avaliar os resultados para a fórmula A ʌ B. Veja na Figura 2 que na primeira coluna (C1) colocamos a proposição A, na segunda coluna (C2) a proposição B e na terceira coluna (C3) a fórmula que queremos avaliar. Sobre os resultados, vamos analisar linha a linha.

Na linha 1 (L1), colocamos as proposições A e B com entrada V. Veja na coluna 3 (C3) que a saída para essas entradas também é V.

Na linha 2 (L2), colocamos a proposição A com entrada V e a B com entrada F. Veja na coluna 3 (C3) que a saída para essas entradas é F.

Na linha 3 (L3), colocamos a proposição A com entrada F e a B com entrada V. Veja na coluna 3 (C3) que a saída para essas entradas é F.

Na linha 4 (L4), colocamos as proposições A e B com entrada F. Veja na coluna 3 (C3) que a saída para essas entradas é F.

	C1	C2	C3
	A	B	$A\wedge B$
L1	V	V	V
L2	V	F	F
L3	F	V	F
L4	F	F	F

Tabela 2 | Tabela verdade de conjunção

Reflita Como usamos duas proposições, foram necessárias 4 linhas para gerar a valoração da fórmula A ʌ B. Repare na distribuição das entradas. Para a proposição A, primeiro foram dispostas as entradas V combinando com as entradas V e F da proposição B; em seguida, foram dispostas as entradas F combinando com as entradas V e F de B. Portanto, a primeira coluna ficou com entradas VVFF e a segunda coluna VFVF. Será que foi só uma coincidência ou existe uma lógica que ajuda na organização? Como ficariam dispostas as entradas da Tabela Verdade da conjunção para três proposições?

Quando utilizamos a lógica formal na construção de algoritmos, o conector lógico AND é um recurso muito valioso na tomada de decisões. O resultado dessa operação em uma linguagem de programação pode ser descrito por meio de uma tabela verdade. Por isso, entender esse mecanismo é fundamental para sua vida profissional.

Exemplificando

Vejamos um exemplo prático para a conjunção. Imagine que estamos criando uma aplicação que precisa informar se uma determinada pessoa irá pagar imposto ou não, a depender da sua renda, de acordo com a seguinte regra: Se o salário for superior a 5 mil e a idade menor que 40 anos, a pessoa pagará de imposto 10% do seu salário. Considere as seguintes proposições:

A: o salário é maior que R$ 5 mil.

B: a idade é menor que 40 anos.

Com base na tabela verdade da conjunção, vamos analisar qual seria o resultado da fórmula A ʌ B para uma pessoa que recebe um salário de R$ 4 mil e possui 32 anos.

Avaliando a proposição A para o caso, temos um resultado F (pois não ganha salário de 5 mil). Já a proposição B possui resultado V (a idade é menor que 40 anos).

Ao consultarmos a terceira linha da Figura 2, vemos que o resultado de A ʌ B para tais entradas é falso. Portanto, para o caso analisado, o resultado da fórmula é F.

Tabela verdade de disjunção (or-ou)

O conector lógico de disjunção (OR - OU) é utilizado para realizar uma operação binária entre duas proposições quando se deseja obter um resultado falso se, e somente se, as duas proposições forem falsas. Utilizaremos o símbolo ˅ para representar esse conector lógico. Para construir a tabela verdade da disjunção, vamos considerar como entradas as proposições A e B. Queremos avaliar os resultados para a fórmula A ˅ B. Veja na Tabela 3 que na primeira coluna colocamos a proposição A, na segunda coluna a proposição B e na terceira coluna a fórmula que queremos avaliar. Sobre os resultados, vamos analisar linha a linha.

Na linha 1 (L1), colocamos as proposições A e B com entrada V. Veja na coluna 3 (C3) que a saída para essas entradas também é V.

Na linha 2 (L2), colocamos a proposição A com entrada V e a B com entrada F. Veja na coluna 3 (C3) que a saída para essas entradas é V.

Na linha 3 (L3), colocamos a proposição A com entrada F e a B com entrada V. Veja na coluna 3 (C3) que a saída para essas entradas é V.

Na linha 4 (L4), colocamos as proposições A e B com entrada F. Veja na coluna 3 (C3) que a saída para essas entradas é F.

	C1	C2	C3
	A	B	$A\wedge B$
L1	V	V	V
L2	V	F	V
L3	F	V	V
L4	F	F	F

Tabela 3 | Tabela verdade com operador OR

 

Como mostra a tabela verdade da disjunção, basta que uma entrada seja verdadeira para obtermos um resultado verdadeiro.

Tabela verdade para negação

O operador lógico de negação tem a função de inverter, seja uma entrada ou o resultado de uma operação. Utilizaremos o símbolo ¬ para representar esse conector lógico. Na Tabela 4 (a), temos uma Tabela Verdade com negação para as proposições A, B. Veja que ¬A inverte o valor de A, ou seja, onde é V fica F e vice-versa. O mesmo acontece para ¬B, que inverte o valor de B. Na Tabela 4 (b), temos nas colunas 3 (C3) e 5 (C5) os resultados já conhecidos da conjunção e disjunção, e nas colunas 4 (C4) e 6 (C6) os novos resultados, sendo na coluna 4 (C4) os resultados para a negação da conjunção e na coluna 6 (C¨) a negação da disjunção. Repare nos parênteses, que são obrigatórios, indicando que a negação é para toda a operação e não somente para uma proposição.

 

a) 

A	B	¬A	¬B
V	V	F	F
F	F	V	V

Tabela 4 | Tabela verdade com operador de negação (a)

b) 

	C1	C2	C3	C4	C5	C6
	A	B	$A\wedge B$	$\neg (A\wedge B)$	$A\vee B$	$\neg (A\vee B)$
L1	V	V	V	F	V	F
L2	V	F	F	V	V	F
L3	F	V	F	V	V	F
L4	F	F	F	V	F	V

Tabela 4 | Tabela verdade com operador de negação (b)

 

Para ficar claro como os parênteses podem afetar o resultado da operação lógica envolvendo a negação, observe a Tabela 5. Na coluna 4 (C4), temos os resultados para a fórmula ¬ (A ∧ B), já na coluna 5 (C5) temos o resultado para a fórmula (A ∧¬ B). Veja como é diferente. No primeiro caso estamos invertendo o resultado da operação toda, já no segundo caso, estamos invertendo apenas o valor de B e fazendo a conjunção com A.

	C1	C2	C3	C4	C5
	A	B	¬B	$\neg (A\wedge B)$	$(A\vee \neg B)$
L1	V	V	F	F	F
L2	V	F	V	V	V
L3	F	V	F	V	F
L4	F	F	V	V	F

Tabela 5 | Tabela verdade com operadores (negação-and)

 

Como você já deve ter percebido, não adianta tentar decorar os resultados, você precisa entender os operadores básicos e, a partir daí, ir resolvendo as fórmulas, parte por parte, com auxílio da tabela verdade.

Vamos Exercitar?

Chegou o momento de solucionarmos o desafio.

Como membro da equipe de analytics de uma empresa de varejo, dadas as seguintes proposições: p: o cliente é do sexo feminino e q: o cliente tem idade entre 20 e 30 anos, você foi encarregado de construir uma Tabela Verdade para as operações de conjunção e disjunção, além de criar a negação para as fórmulas. Com a Tabela Verdade criada, você deve avaliar os registros de clientes que foi lhe passado na Tabela 1, completando as colunas E/OU com V ou F.

A tabela verdade é um mecanismo que permite valorar fórmulas de forma genérica a partir de entradas binárias e conectores lógicos. Pois bem, como o problema proposto apresenta duas proposições, serão necessárias 4 linhas para contemplar todas as combinações possíveis das entradas. Além disso, serão necessárias 6 colunas, sendo 2 para as proposições (p, q), uma para a fórmula da conjunção, outra para a disjunção, outra para a negação da conjunção e uma última com a negação da disjunção. O resultado da tabela verdade deve estar conforme o Quadro 1.

p	q	$p\wedge q$	$p\vee q$	$\neg (p\wedge q)$	$\neg (p\vee q)$
V	V	V	V	F	F
V	F	F	V	V	F
F	V	F	V	V	F
F	F	F	F	V	V

A tabela verdade pode ser usada como um gabarito para as operações lógicas, pois contempla todas as entradas possíveis e suas combinações para as fórmulas em estudo. Com esse gabarito em mãos, podemos passar para a segunda etapa do desafio, que é fazer a valoração das fórmulas p ʌ q e p ˅ q para cada registro da base de clientes. Pois bem, vejamos na Tabela 2, como ficaram os resultados.

linha	codigo_cli	nome_cli	genero_cli	idade_cli	valor_compra	E	OU
1	53682	Karly Dillon	F	40	74,84	F	V
2	58246	Channing Vazquez	M	49	98,04	F	F
3	27022	Adria Key	F	47	65,93	F	V
4	82075	Ella Nelson	F	34	94,01	F	V
5	90657	Arden Battle	M	48	21,73	F	V
6	80330	Brittany Ramirez	F	38	42,23	F	F
7	53989	Moses Graham	M	42	37,20	F	V
8	61370	Jin Fuller	M	49	65,60	F	F
9	41807	Phelan Blair	M	46	77,40	F	F
10	94269	Porter West	M	22	67,19	F	V

Nossa maior lição com esse desafio é entender como uma questão de lógica formal pode ser utilizada em um algoritmo, e isso, no mercado de trabalho, fornece resultados para as mais diversas áreas de uma empresa. Se fornecêssemos para a equipe de vendas o resultado da coluna da conjunção, a fim de comunicá-los sobre o lançamento de uma nova promoção, nenhum desses 10 receberia tal comunicado, por outro lado, se nosso resultado fosse baseado na disjunção, vários deles receberiam o comunicado.

É isso aí, você como um profissional deve ter consciência das suas responsabilidades e tomar as melhores decisões para a empresa!

Saiba Mais

Construção da tabela verdade são fundamentais para a compreensão da disciplina Lógica e matemática computacional. A seguir, algumas indicações para um estudo profundo sobre o tema.

1. BISPO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. S. Introdução à lógica matemática. Cengage Learning Brasil, 2017. O capítulo 2 deste livro aborda os tópicos referentes a: (1) Tabela verdade, (2) Disjunção (3) Conjunção e (4) Negação.
2. QUILELLI, P. Raciocínio lógico matemático para concursos. 3. ed. Editora Saraiva, 2015. O capítulo 2 aborda os tópicos relacionados à tabela verdade, negação, conjunção e disjunção.

Referências Bibliográficas

BISPO FILHO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à lógica matemática. São Paulo: Cengage Learning, 2017.

FAJARDO, R. Lógica matemática. 1. ed. São Paulo: Edusp, 2017.

MUNDIM, R. P. A Lógica Formal – princípios elementares. Revista Economia & Gestão, Belo Horizonte, v. 2, n. 3, jan./jun. 2002.

SANTOS, M. da S. dos et al. Lógica computacional. Grupo A, 2021. 

Resultados da tabela verdade

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Olá, estudante! Os profissionais das mais diversas áreas tomam decisões o tempo todo em seu ambiente de trabalho. Todas as decisões precisam ser bem avaliadas, pois toda ação gera uma consequência. Por exemplo, em uma campanha promocional, se optar por desconto a um determinado grupo, poderá não vender tanto para um outro grupo potencial. No mundo da lógica computacional, as decisões são tomadas por meio de estruturas de decisão, que têm sua origem em um conector lógico chamado de implicação, o qual veremos sua tabela verdade nesta seção.

Como funcionário trainee na área de analytics de uma empresa de varejo, você deve ajudar a equipe de marketing em uma campanha para o dia internacional da mulher.

Dadas as proposições:

A: o cliente é do sexo feminino.

B: o cliente fez um compra com valor superior a R$ 50,00.

C: ganhar cupom com 10% de desconto.

Seu desafio consiste primeiro em avaliar a fórmula A ˄ B para cada um dos registros da Tabela 1. Essa avaliação lhe permitirá classificar a proposição C para cada um dos clientes, ou seja, se o cliente ganhará ou não o cupom de 10% de desconto.

Após a classificação, você deverá generalizar, por meio de uma tabela verdade, as possíveis respostas para a fórmula P → Q, sendo P e Q duas proposições genéricas.

codigo_cli	nome_cli	genero_cli	idade_cli	valor_compra	cupom_10
53682	Karly Dillon	F	40	74,84	?
58246	Channing Vazquez	M	49	98,04	?
27022	Adria Key	F	47	65,93	?
82075	Ella Nelson	F	34	94,01	?
90657	Arden Battle	M	48	21,73	?
80330	Brittany Ramirez	F	38	42,23	?
53989	Moses Graham	M	42	37,20	?
61370	Jin Fuller	M	49	65,60	?
41807	Phelan Blair	M	46	77,40	?
94269	Porter West	M	22	67,19	?
56516	Zena Skinner	F	54	73,98	?
38904	Teagan Rios	M	34	61,57	?

Tabela 1 | Dados de compra dos clientes

Para cumprir seu desafio, nesta seção veremos a tabela verdade do conector de implicação, bem como outros importantes resultados da tabela verdade.

Pronto para o desafio?!

Vamos Começar!

Definição

A tabela verdade é utilizada como um método exaustivo de extração de resultados. Em outras palavras, construímos uma tabela verdade para testarmos todos os resultados possíveis para todas as combinações possíveis de entradas em uma determinada fórmula. Uma fórmula é composta por proposições e operadores lógicos, como, por exemplo, a negação (NOT), a conjunção (AND) e a disjunção (OR). Além desses conectores, as proposições podem ser combinadas na forma “se proposição 1, então proposição 2”. O conectivo lógico dessa combinação é o condicional, representado por →, e significa que se a proposição 1 é verdadeira, implicará na verdade da proposição 2. Em outras palavras, podemos dizer que dada uma sequência de proposições, a partir da operação condicional é possível chegar a uma conclusão (um resultado), que é uma nova proposição. A primeira parte, antes do conector, é chamada de antecedente, e a segunda de consequente conforme ilustra a Figura 1.

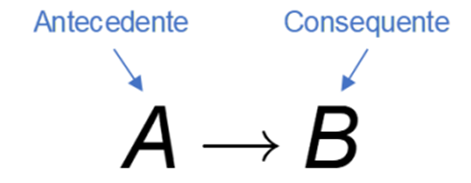
Para entendermos como funciona a implicação, vejamos alguns exemplos.

Considere as proposições A e B:

A: há uma falha na rede elétrica.

B: a chave central irá desligar.

A fórmula A → B, que significa que B está condicionado a A, deve ser lida como: “se houver uma falha na rede elétrica, então, a chave central irá desligar.

Considere as proposições P, Q, R.

 P: a nota mínima necessária para ser aprovado é 6,0.

Q: João tirou 8,0 na prova.

R: João será aprovado.

Nesse exemplo, temos o resultado de uma conjunção implicando uma terceira proposição. Simbolicamente, escrevemos (P ∧ Q) → R, e deve ser lida como: “Se a nota mínima necessária para ser aprovado é 6,0 e João tirou 8,0 na prova, então, ele será aprovado.”

Os possíveis resultados do operador condicional estão representados na tabela verdade apresentada na Tabela 1.

	C1	C2	C3
	A	B	$A\to B$
L1	V	V	V
L2	V	F	F
L3	F	V	V
L4	F	F	V

Tabela 1 | Tabela verdade para o condicional

Para entendermos os resultados da implicação, vejamos o seguinte exemplo.

A: soltar a pedra.

B: a queda da pedra.

A fórmula A → B deve ser lida como “Se a pedra for solta, então, a pedra cairá”. Agora, vamos avaliar todas as respostas possíveis com base na tabela verdade da Figura 2. Na primeira linha (L1), temos como entrada a verdade das proposições A e B, em nosso exemplo, quer dizer que a pedra foi solta (proposição A é verdadeira) e caiu (proposição B é verdadeira), portanto, a condição era verdadeira e o resultado é V (linha 1 e coluna 3). Na linha dois (L2), temos como entrada que a proposição A é verdadeira e a proposição B é falsa, isso quer dizer que a pedra foi solta, mas não caiu. Nesse caso, a condicional não é verdadeira e o resultado é F (linha 2 e coluna 3). Nas demais linhas, terceira e quarta (L3 e L4), temos como entrada que a proposição A é falsa (que é o antecedente), nesse caso, não há como avaliar a condicional e o resultado é tomado como verdadeiro.

Assimile Os resultados lógicos das linhas 3 e 4 (L3 e L4) da tabela verdade da condicional não são tão fáceis de identificar. Como se trata de uma dependência, caso o antecedente seja falso, o resultado lógico será sempre verdadeiro. “Por convenção, A → B será considerada verdadeira se A for falsa, independentemente do valor lógico de B”.

Siga em Frente...

Tautologia, contradição e contingência

Considerando a proposição A como:

A: hoje está chovendo.

Vamos construir a tabela verdade para a fórmula A ∨ ¬A, que, traduzindo, quer dizer, “hoje está chovendo ou hoje não está chovendo”. Veja o resultado no Quadro 2.

A	$\leftarrow A$	$A\vee \neg A$
V	F	V
F	V	V

Quadro 2 | Tabela verdade da fórmula A ∨ ¬A

Como podemos observar no Quadro 1, a coluna dos resultados (última coluna) para a fórmula obteve como resposta somente verdadeiro. Quando o resultado de uma fórmula obtém somente V como resposta, a fórmula é denominada tautologia.

Agora, vamos considerar a seguinte proposição B: B: hoje é segunda-feira. Vamos construir a Tabela verdade para a fórmula B ∧ ¬B, que quer dizer, “Hoje é segunda-feira e hoje não é segunda-feira”. Veja o resultado na Quadro 3.

B	$\leftarrow B$	$B\vee \neg B$
V	F	F
F	V	F

Quadro 3 | Tabela verdade da fórmula B ∧ ¬B

Como podemos observar no Quadro 2, a coluna dos resultados (última coluna da tabela verdade) para a fórmula obteve como resposta somente falso. Quando o resultado de uma fórmula obtém somente F como resposta, a fórmula é denominada contradição.

Quando uma tabela verdade não é uma tautologia e não é uma contradição, então, ela é uma contingência.

Reflita A tautologia é uma proposição em que, independentemente das entradas, todas as respostas são verdadeiras. Já a contradição é o resultado quando todas as possíveis respostas são falsas. Podemos afirmar que a tautologia acontecerá somente para as fórmulas com conectores lógicos de disjunção (OR) e a contradição para os conectores de conjunção (AND)?

Equivalência aplicada na tabela verdade

Considere as seguintes proposições:

A: o cliente tem 35 anos.

B: o cliente gastou mais do que R$ 100,00 na última compra.

 

Dadas as proposições A e B, vamos construir a Tabela verdade (Quadro 4) para as seguintes fórmulas: A ˅ B e B ˅ A.

A	B	$A\vee B$	$A\wedge B$	$A\vee B\iff B\vee A$
V	V	V	V	V
V	F	V	V	V
F	V	V	V	V
F	F	F	F	V

Quadro 4 | Tabela verdade das fórmulas A ˅ B e B ˅ A

As colunas 3 e 4 do Quadro 3 apresentam os possíveis resultados para as fórmulas A ˅ B e B ˅ A. Na quinta coluna, temos mais um teste lógico chamado de equivalência, no qual testamos se os resultados obtidos para a fórmula A ˅ B são iguais (equivalentes) aos obtidos por B ˅ A. Veja que usamos o símbolo ↔ para denotar essa operação e que o resultado foi uma tautologia, o que nos permite concluir que as fórmulas A ˅ B e B ˅ A são equivalentes.

Exemplificando

Para saber se duas fórmulas são equivalentes, é necessário construir a tabela verdade e verificar se a equivalência é uma tautologia. Por exemplo, vamos construir uma tabela verdade (Quadro 5) para testar se as fórmulas A ˄ B e B ˄ A são equivalentes.

A	B	$A\wedge B$	$B\wedge A$	$A\wedge B\iff B\wedge A$
V	V	V	V	V
V	F	F	F	V
F	V	F	F	V
F	F	F	F	V

Quadro 5 | Tabela verdade das fórmulas A ˄ B e B ˄ A

Como podemos observar no Quadro 4.6, as fórmulas A ˄ B e B ˄ A também são equivalentes.

Os resultados obtidos nos quadros 3 e 4 não são uma coincidência, pois estamos diante de uma forte propriedade, a comutativa. Lembra das aulas de matemática quando aprendeu que o resultado de 2 + 3 é igual a 3 + 2? Pois bem, aqui na lógica também temos essa mesma propriedade: a ordem dos fatores não altera o resultado. Veja no Quadro 6 mais algumas propriedades.

1	$A\vee B\iff B\vee A$	$A\wedge B\iff B\wedge A$	Comutatividade
2	$(A\vee B)\vee C\iff A\vee (B\vee C)$	$(A\vee B)\vee C\iff A\vee (B\vee C)$	Associatividade
3	$A\vee (B\wedge C)\iff (A\vee B)\wedge (A\vee C)$	$A\wedge (B\vee C)\iff (A\wedge B)\vee (A\wedge C)$	Distributividade

Quadro 6 | Equivalências tautológicas

Já vimos as tabelas verdade para a propriedade da comutatividade, vejamos agora para as demais, começando pela associativa (A ∨ B) ∨ C ⇔ A ∨ (B ∨ C). O resultado está no Quadro 7. O primeiro detalhe é que, como temos três proposições envolvidas, vamos precisar de 8 linhas para representar todas as combinações possíveis (lembra, linhas = 2ⁿ). Outro detalhe é que para facilitar, resolvemos a fórmula em partes. Veja: na coluna C4, extraímos os resultados para A ∨ B, e na coluna C5 utilizamos o resultado de C4 para fazer a disjunção com a proposição C, obtendo o resultado do lado esquerdo da fórmula. O mesmo fizemos para o lado direito, na coluna C6, fizemos B ∨ C (como estava entre parênteses, fizemos primeiro) e depois, na coluna C7, utilizamos o resultado de C6 para fazer a disjunção com a proposição A. Por fim, na coluna C8, fizemos a equivalência verificando se os resultados obtidos em C5 e C7 eram iguais, como temos uma tautologia, então, podemos afirmar que elas de fato são equivalentes.

C1	C2	C3	C4	C5	C6	C7	C8
A	B	C
V	V	V	V	V	V	V	V
V	V	F	V	V	V	V	V
V	F	V	V	V	V	V	V
V	F	F	V	V	F	V	V
F	V	V	V	V	V	V	V
F	V	F	V	V	V	V	V
F	F	V	F	V	V	V	V
F	F	F	F	F	F	F	V

Quadro 7 | Tabela verdade para propriedade associativa (A ∨ B) ∨ C ⇔ A ∨ (B ∨ C)

Vamos agora verificar uma equivalência da propriedade da distributividade para a fórmula A ∧ (B ∨ C) ⇔ (A ∧ B) ∨ (B ∧ C). O Quadro 8 apresenta o resultado. Resolvemos primeiro o lado esquerdo da equivalência, ou seja, a fórmula A ∧ (B ∨ C). Na coluna C4 fizemos a disjunção entre parênteses e na coluna C5 utilizamos o resultado obtido em C4 para fazer a conjunção com a proposição A. Nas colunas C6 e C7, resolvemos os parênteses da fórmula à direita da equivalência, e na C8, usamos os resultados de C6 e C7 para a disjunção. Por fim, na C9 comparamos os resultados obtidos em C5 e C8, provando que se trata de uma equivalência.

C1	C2	C3	C4	C5	C6	C7	C8	C9
A	B	C
V	V	V	V	V	V	V	V	V
V	V	F	V	V	V	F	V	V
V	F	V	V	V	F	V	V	V
V	F	F	F	F	F	F	F	V
F	V	V	V	F	F	F	F	V
F	V	F	V	F	F	F	F	V
F	F	V	V	F	F	F	F	V
F	F	F	F	F	F	F	F	V

Quadro 8 | Tabela verdade para a propriedade da distributividade A ∧ (B ∨ C) ⇔ (A ∧ B) ∨ (B ∧ C)

Não poderíamos encerrar esta seção sem mencionar, além das propriedades, outros dois importantes resultados da equivalência, usados para fazer a negação de uma proposição composta. As duas equivalências são:

I - ¬ (A ∨ B) ⇔ ¬A ∧¬B

II - ¬ (A ∧ B) ⇔ ¬A ∨¬ B

Observe que a primeira equivalência (I) trata da equivalência envolvendo a negação em uma disjunção e a segunda equivalência (II) corresponde a uma negação em uma conjunção. O Quadro 8 apresenta os resultados para a fórmula I e o Quadro 9 para a fórmula II.

A	B	$\neg (A\vee B)$	$\neg A\wedge \neg B$	$\iff$
V	V	F	F	V
V	F	F	F	V
F	V	F	F	V
F	F	V	V	V

Quadro 9 | Tabela verdade para a Lei De Morgan ¬ (A ∨ B) ⇔ ¬A ∧¬B

A	B	$\neg (A\wedge B)$	$\neg A\vee \neg B$	$\iff$
V	V	F	F	V
V	F	V	V	V
F	V	V	V	V
F	F	V	V	V

Quadro 10 | Tabela verdade para a Lei De Morgan ¬ (A ∧ B) ⇔ ¬A ∨¬ B

O que podemos concluir das Leis De Morgan é que a negação de uma disjunção é equivalente à negação de cada uma das proposições em uma conjunção (fórmula I) e que a negação de uma conjunção é equivalente à negação de cada uma das proposições em uma disjunção (fórmula II).

Vamos Exercitar?

Você foi encarregado da missão de direcionar a equipe de marketing em uma campanha para o dia internacional da mulher.

Dada as proposições:

A: o cliente é do sexo feminino.

B: o cliente fez um compra com valor superior a R$ 50,00.

C: ganhar cupom com 10% de desconto.

Você deve primeiro avaliar a fórmula A ∧ B para cada um dos registros da Tabela 1 classificando a proposição C, como V ou F, para cada um dos clientes, ou seja, se o cliente ganhará ou não o cupom de 10% de desconto.

Pois bem, vamos analisar o primeiro registro:

A: O cliente é do sexo feminino. (SIM – V)

B: O cliente fez um compra com valor superior a R$ 50,00. (SIM – V)

Portanto, para o primeiro registro a fórmula A B Ù resulta em V, pois V ∧ V = V, então a proposição C é V.

Já para o segundo registro, temos F ∧ V = F, pois o cliente é do sexo masculino. Então a proposição C é falsa para esse caso.

Ao analisar todos os registros, você deve chegar ao resultado da Tabela 11.

linha	codigo_cli	nome_cli	genero_cli	idade_cli	valor_compra	cupom_10
1	53682	Karly Dillon	F	40	74,84	V
2	58246	Channing Vazquez	M	49	98,04	F
3	27022	Adria Key	F	47	65,93	V
4	82075	Ella Nelson	F	34	94,01	V
5	90657	Arden Battle	M	48	21,73	F
6	80330	Brittany Ramirez	F	38	42,23	F
7	53989	Moses Graham	M	42	37,20	F
8	61370	Jin Fuller	M	49	65,60	F
9	41807	Phelan Blair	M	46	77,40	F
10	94269	Porter West	M	22	67,19	F
11	56516	Zena Skinner	F	54	73,98	V
12	38904	Teagan Rios	M	34	61,57	F

Tabela 2 | Resultado para a equipe de marketing

Agora, vamos generalizar as repostas construindo a tabela verdade para a fórmula P→ Q, como mostra o Quadro 11.

P	Q	$P\to Q$
V	V	V
V	F	F
F	V	V
F	F	V

Quadro 11 | Tabela verdade para a fórmula P→ Q,

Para finalizar, vamos fazer a conexão entre o resultado obtido na análise dos registros com o Quadro 4.10.

A primeira observação importante é que a proposição genérica P no desafio é o resultado da conjunção A ∧ B. Vamos fazer a análise com os dois primeiros registros.

No primeiro registro, a fórmula A ∧ B resultado em V e a proposição C também foi classificada como V. Temos aqui o caso V → V, que, consultado a tabela verdade da implicação tem como resultado também V, isso quer dizer que a proposição “O cliente é do sexo feminino e fez uma compra acima de R$ 50,00, então, ele ganhará desconto” é uma verdade.

Já para o segundo registro, temos A ∧ B = F, consequentemente a proposição C também é falsa. Temos aqui o caso F → F, que consultado a tabela verdade da implicação, tem como resultado V, mas o que esse resultado quer dizer? Quer dizer que a proposição “O cliente não é do sexo feminino e nem fez uma compra acima de R$ 50,00, então, ele não ganhará desconto” é uma verdade.

Termine de fazer as avaliações, caso a caso, pois quanto mais praticar, mais apto estará para avaliar as implicações lógicas e contribuir ainda mais com seu time!

Saiba Mais

Resultados da tabela verdade são fundamentais para a compreensão da disciplina Lógica e Matemática Computacional. A seguir, algumas indicações para um estudo profundo sobre o tema.

1. BISPO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. S. Introdução à Lógica Matemática. Cengage Learning Brasil, 2017. E-book. ISBN 9788522115952. [Minha Biblioteca]. O capítulo 2 deste livro aborda os tópicos referentes: (1) à Tabela verdade, (2) aos Critérios para a tabela verdade e (3) aos Exercícios.
2. QUILELLI, P. Raciocínio lógico matemático para concursos. 3. ed. Editora Saraiva, 2015. O capítulo 2 aborda os tópicos relacionados à tabela verdade.

Referências Bibliográficas

BISPO FILHO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à lógica matemática. São Paulo: Cengage Learning, 2017.

FAJARDO, R. Lógica matemática. 1. ed. São Paulo: Edusp, 2017.

MUNDIM, R. P. A Lógica Formal – princípios elementares. Revista Economia & Gestão, Belo Horizonte, v. 2, n. 3, jan./jun. 2002.

SANTOS, M. da S. dos et al. Lógica computacional. Grupo A, 2021.

Aplicações da tabela verdade

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Partida

Olá, estudante! Até você chegar ao ensino superior foram anos de estudos, não é mesmo? Tudo começou com o processo de alfabetização, tanto de leitura quanto das operações básicas de matemática (soma, subtração, divisão e multiplicação). Primeiro você aprendeu a fazer operações matemáticas simples, por exemplo, 2 + 3, depois apareceram os parênteses, por exemplo, (2 + 3) × 4. Mas será que esses parênteses são só de enfeite? Certamente que não! Eles influenciam a ordem que as operações devem ser resolvidas e, como você já deve saber, não seguir as regras certamente implica em chegar em resultados errôneos. Pois bem, da mesma forma que a matemática tem suas fórmulas e suas regras de resolução, a lógica formal também as possui, e nesta seção vamos aprender mais sobre elas.

Como funcionário trainee na área de analytics de uma empresa de varejo, você deve dar continuidade em seu trabalho, fornecendo novos insights para a equipe de marketing realizar sua campanha promocional. Para esse novo desafio foi enviada a você uma base com novas informações, conforme ilustra a Tabela 1. Nessa base é possível encontrar o valor gasto na última compra do cliente, o total de compras já feito por ele e o ticket médio (valor médio gasto em cada compra). A partir desses dados você deve usar as regras da lógica para classificar se o cliente tem potencial para comprar na nova campanha e, se tiver, então ele ganhará um cupom com desconto de 10%. Caso não seja um cliente com potencial então ele ganhará somente um cupom com 5%. Vamos às regras: para ser classificado como um cliente com potencial de compra, não importa o gênero (pode ser feminino ou masculino), o cliente deve ter idade entre 30 e 45 anos, ter feito acima de 10 compras e ter um ticket médio acima de R$ 50,00. Seu desafio é montar uma fórmula que traduza essa regra e, então preencher a coluna “cliente_potencial” com o resultado da fórmula para cada registro. Dada a classificação, você deve escrever uma nova fórmula que traduza “Se o cliente tem potencial de compra, então ele deve ganhar um cupom com 10% de desconto”, e outra fórmula que traduza “Se é falso que o cliente tem potencial de compra, então ele deve ganhar um cupom com 5% de desconto”. Por fim, use a lógica de programação para preencher as colunas “cupom_10” e “cupom_5” valorando as condicionais.

codigo_ cli	nome_ cli	genero_cli	idade_cli	valor_ compra	total_ compras	Ticket_ medio	cliente_ potencial	cupom_10	cupom_5
53682	Karly Dillon	F	40	74,84	5	45,00	?	?	?
58246	Channing Vazquez	M	49	98,04	20	200,00	?	?	?
27022	Adria Key	F	47	65,93	12	34,00	?	?	?
82075	Ella Nelson	F	34	94,01	16	150,00	?	?	?
90657	Arden Battle	M	48	21,73	4	23,00	?	?	?
80330	Brittany Ramirez	F	38	42,23	1	42,23	?	?	?
53989	Moses Graham	M	42	37,20	29	45,00	?	?	?
61370	Jin Fuller	M	49	65,60	35	123,00	?	?	?
41807	Phelan Blair	M	46	77,40	23	95,00	?	?	?
94269	Porter West	M	22	67,19	6	35,00	?	?	?
56516	Zena Skinner	F	54	73,98	15	60,00	?	?	?
38904	Teagan Rios	M	34	61,57	17	71,00	?	?	?

Tabela 1 | Dados de compra dos clientes

Para cumprir esse desafio, nesta seção você aprenderá a importância dos parênteses nas fórmulas, bem como seguir a regra de precedência dos operadores. Você também verá um caso de como fazer a ligação entre a lógica formal e a lógica na computação, assim já vai se preparando para em breve começar a programar.

Então vamos lá!

Vamos Começar!

Ao longo de nossos estudos aprendemos diversas fórmulas; quem não se lembra da famosa fórmula de Bhaskara usada para encontrar as raízes de uma equação do segundo grau? Ou então da segunda lei Newton, que diz que a força é sempre diretamente proporcional ao produto da aceleração de um corpo pela sua massa? Para conseguimos resolver esses tipos de equação, primeiro foi necessário aprender as operações matemáticas básicas (soma, subtração, multiplicação e divisão); depois essas operações passaram a se combinar em fórmulas mais elaboradas, e nesse momento foi necessário aprender a ordem de precedência dos operadores. Por exemplo: as fórmulas: (i) 2 + 3 × 4 e (ii) (2 +3) × 4 apresentam o mesmo resultado? A resposta é não, pois a primeira tem como resultado 14 e a segunda, 20. Isso acontece porque, em uma fórmula, a multiplicação tem precedência sobre adição, então ao não usar parênteses na fórmula (i) a multiplicação foi feita antes da soma. Outro detalhe importante é que as fórmulas apresentam uma sintaxe correta, por exemplo: não podemos escrever 2 ++ 3, pois essa fórmula é inválida.

Assim como as fórmulas matemáticas, podemos construir expressões lógicas mais complexas a partir da combinação das proposições, dos conectivos e dos parênteses. Da mesma forma que as operações matemáticas têm ordem de precedência, os conectivos lógicos também a possui.

Assimile Para resolver uma expressão lógica que combina várias proposições com conectivos lógicos é preciso obedecer a seguinte regra de precedência: 1. Para expressões que tenham parênteses, primeiro efetuam-se as operações lógicas dentro dos parênteses mais internos. 2. ¬ (Negação) (maior precedência). 3. ∧ ∨, (Conjunção e disjunção). 4. → (Implicação). 5. ↔ (Bicondicional).

Ao seguir rigorosamente a ordem de precedência dos operadores, o uso de parênteses pode ser omitido nos casos adequados. Por exemplo: a fórmula A ∨ (¬B) pode simplesmente ser escrita como A ∨ (¬B), uma vez que, de acordo com a ordem de precedência, a negação será realizada primeiro, mesmo sem parênteses.

Exemplificando

Para exemplificar como a ordem de precedência dos operadores lógicos pode influenciar o resultado, vamos construir uma tabela verdade para as fórmulas A ∧ B → A e A ∨ (B → A). Veja no Quadro 1 que os resultados das colunas C4 e C6 são diferentes. Em C4, como o operador de conjunção tem precedência sobre a implicação, chegamos em uma tautologia, o que não ocorreu em C6 quando forçamos, por meio de parênteses, a implicação ser efetuada primeiro.

C1	C2	C3	C4	C5	C6
A	B	$A\wedge B$	$A\wedge \to B\to A$	$B\to A$	$A\wedge \left(B\to A\right)$
V	V	V	V	V	V
V	F	F	V	V	V
F	V	F	V	F	F
F	F	F	V	V	F

Quadro 1 | Tabela verdade das fórmulas A ∧ B → A e A ∨ (B → A)

Ainda no Quadro 1, observe que usamos a coluna C3 para efetuar a primeira operação da fórmula A ∧ B → A, e na coluna C4 usamos o resultado obtido em C3 para fazer a implicação. O mesmo acontece na coluna C5, em que fazemos a primeira operação da fórmula A ∨ (B → A), (considerando as regras da ordem de precedência) e depois usamos o resultado de C5 para fazer a conjunção final em C6. Esse processo de criar uma coluna para cada operação facilita o trabalho e nos auxilia a não cometer erros na construção da tabela verdade. Esses resultados intermediários podem ser representados por novas letras, por exemplo: poderíamos chamar o resultado da coluna C3 de P, então na coluna C4 teríamos P → A. Da mesma forma, poderíamos chamar o resultado da coluna C5 de R, então na coluna C6 teríamos a fórmula A ∧ R. O Quadro 2 mostra essa alternativa.

		P		R
A	B	$A\wedge B$	$P\to A$	$B\to A$	$A\wedge R$
V	V	V	V	V	V
V	F	F	V	V	V
F	V	F	V	F	F
F	F	F	V	V	F

Dada uma fórmula com várias proposições, conectores e parênteses dentro de parênteses, a resolução deve começar pelos parênteses mais internos. Por exemplo, a fórmula ((A ∨ B) → C) ∧ A deve ter a seguinte ordem de resolução:

1 - A ∨ B (parênteses mais internos)

2 - ((A ∨ B → C) (parênteses mais externos)

3 - ((A ∨ B) → C) ∧ A (operação fora dos parênteses).

O Quadro 3 mostra o resultado para essa fórmula. Veja que usamos proposições intermediárias para nomear os resultados. Primeiro obtemos P (A ∨ B) que é o resultado 1, depois usamos para obter Q (P → C), que é o resultado 2, e por fim, o usamos para obter o resultado da fórmula, o qual também nomear, por exemplo R (Q ∧ A).

			P	Q	R
A	B	C	$A\vee B$	$P\to C$	$Q\wedge A$
V	V	V	V	V	V
V	V	F	V	F	F
V	F	V	V	V	V
V	F	F	V	F	F
F	V	V	V	V	F
F	V	F	V	F	F
F	F	V	F	V	F
F	F	F	F	V	F

Quadro 3 | Tabela verdade para a fórmula ((A ∨ B) → C) ∧ A

Reflita Por praxe – mas não obrigatoriamente – construímos a tabela verdade colocando nas colunas mais à esquerda as proposições, em seguida, as colunas com as fórmulas. Em uma fórmula do tipo (A ∨ B) → A, precisamos primeiro obter o resultado de A ∨ B, para depois fazer a implicação. Quando o resultado de uma operação é usado para entrada em outra operação faz diferença a ordem das operações lógicas que serão consideradas? Em outras palavras, nessa operação (A ∨ B) → A, obteremos o mesmo resultado se fizermos A → (A ∨ B)?

Siga em Frente...

Uma dúvida que pode surgir é sobre como vamos aplicar todas essas operações e regras no universo da programação. A resposta é simples: vamos utilizar para construir uma sequência de instruções, chamada de algoritmo.

Um algoritmo é uma sequência de passos que soluciona algum problema de diversas áreas do mundo real. Mais precisamente, as operações lógicas são usadas em estruturas condicionais (ou estruturas de decisão) e têm o objetivo de realizar testes alterando o fluxo de execução de um programa, de acordo com a resposta obtida. Por exemplo, imagine que acabou de se mudar e esteja realizando a busca de um apartamento em um site de aluguel de imóveis. O site oferece uma interface na qual você clica nas opções que deseja, conforme ilustra a Figura 1.

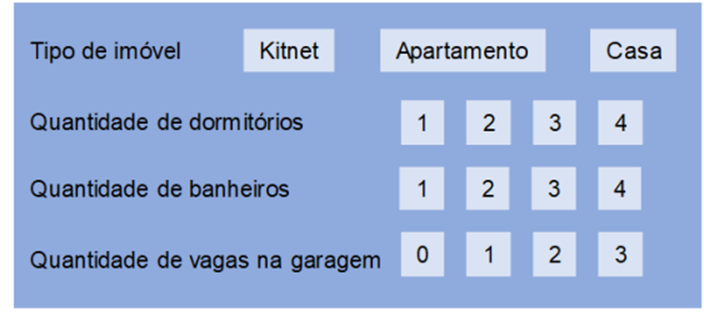
Vamos fazer algumas simulações para avaliarmos a lógica por trás da nossa seleção.

Simulação 1: Selecionar Apartamento; 1 dormitório; 1 banheiro; sem vaga de garagem.

A expressão lógica que será construída com base nessa simulação é:

Apartamento E 1 quarto E 1 banheiro E sem garagem.

Serão exibidos na tela somente os imóveis que satisfazem todas essas alternativas; os demais serão ignorados, pois no algoritmo a instrução é composta pelo conector de conjunção.

Simulação 2: Selecionar Apartamento; 1, 2 dormitórios; 1, 2 banheiros; 0, 1 vaga de garagem.

Nesse caso a expressão lógica será: Apartamento E (1 quarto OU 2 quartos) E (1 banheiro OU 2 banheiros) E (0 OU 1 vaga de garagem).

Veja que nesse caso a expressão é mais complexa e envolve a resolução de parênteses internos. Como resultado da busca apareceriam tanto opções com 1 quanto com 2 quartos e banheiros e sem garagem ou com 1 vaga.

Todas essas opções devem estar implementadas no algoritmo por meio das estruturas condicionais.

Esse tipo de estrutura é amplamente usado em algoritmos computacionais. Quem nunca fez uma compra em um site? Ao finalizar a compra, o algoritmo faz uma conjunção dos itens que colocamos no carrinho de compras, para calcular o preço final.

Para finalizar nossa seção, vamos utilizar uma base com dados reais e, a partir de uma tabela verdade, veremos como classificar os registros. Os dados usados são de domínio público e estão disponíveis no Portal Brasileiro de Dados Abertos.

Trata-se de uma base com os preços de combustíveis em algumas cidades do Brasil no ano de 2019, segregados por estado, cidade, estabelecimento de revenda, produto, data da pesquisa, valor de venda, valor de compra e bandeira do posto, conforme amostra dos dados na Tabela 2.

	Estado	Município	Revenda	Produto	Data da coleta	Valor de venda	Valor de compra	Bandeira
1	DF	Brasília	Abritta Postos de Serviços Ltda.	Diesel S10	23/01/2019	3,899		xx
2	DF	Brasília	Abritta Postos de Serviços Ltda.	Etanol	16/01/2019	3,299	2,9999	xx
3	RJ	Rio de Janeiro	3Posto Julio de Castilho Limitada.	Gasolina	07/03/2019	5,096	4,305	xx
4	DF	Brasília	Abritta Postos de Serviços Ltda.	Etanol	23/01/2019	4,299	3,6745	xx
5	RJ	Rio de Janeiro	3Posto Julio de Castilho Limitada.	Etanol	03/01/2019	3,499	2,9711	xx
6	DF	Brasília	Abritta Postos de Serviços Ltda.	Etanol	23/01/2019	3,197	2,9416	xx
7	DF	Brasília	Abritta Postos de Serviços Ltda.	Gasolina	08/01/2019	4,187	3,735	xx
8	SC	Blumenau	Auto Posto 7 Ltda.	Diesel S10	02/01/2019	3,597		xx
9	SC	Blumenau	Auto Posto 7 Ltda.	Gasolina	12/02/2019	3,767		xx

Tabela 2 | Amostra dos dados de combustíveis automotivos

Dadas as seguintes proposições:

A: O município é Brasília.

B: O combustível é gasolina.

C: A bandeira é Petrobras.

Vamos construir a tabela verdade para a regra “Se a cidade não for Brasília e o combustível for gasolina então a bandeira é Petrobras.”. Em seguida, vamos fazer a conexão entre a lógica formal com a lógica computacional, mais especificamente com a lógica de programação, para avaliar a regra para cada um dos registros. O primeiro passo é traduzir a regra para uma fórmula lógica, o que nos resulta em (¬A ∧ B) → C. O resultado da tabela verdade para a fórmula está no Quadro 4. Veja que a primeira operação que fizemos foi a negação, que está dentro dos parênteses (seguindo a ordem de precedência dos operadores), depois fizemos a conjunção e chamamos o resultado de R. Usamos esse resultado para fazer a implicação.

				R
A	B	C	$\leftarrow A$	$\neg A\wedge B$	$R\to C$
V	V	V	F	F	V
V	V	F	F	F	V
V	F	V	F	F	V
V	F	F	F	F	V
F	V	V	V	V	V
F	V	F	V	V	F
F	F	V	V	F	V
F	F	F	V	F	V

Lembrando que a tabela verdade nos permite avaliar a veracidade da expressão testando todas as combinações possíveis. Vamos interpretar alguns resultados do Quadro 4. Na linha 1, temos a seguinte expressão “Se é falso que a cidade não é Brasília e o combustível é gasolina, então a bandeira é Petrobras.”. Tal expressão tem como resultado V, que se deve à falsidade no antecedente, impossibilitando avaliar o resultado que, portanto, é tomado como verdadeiro. Na linha 2, a expressão é “Se é falso que a cidade não é Brasília e o combustível é gasolina, então é falso que a bandeira é Petrobras”. Dada a falsidade no antecedente e consequente, a expressão tem como resultado V. O único caso em que a implicação tem como resultado F, é quando o antecedente é verdadeiro e o consequente é falso.

Os operadores lógicos são usados na lógica de programação para dizer se uma condição seja verdadeira ou falsa. Nesse exemplo, queremos criar uma lógica de programação para avaliar regra “Se a cidade não for Brasília e o combustível for gasolina então a bandeira é Petrobras.” Pois bem, o Quadro 5 apresenta o resultado da análise das proposições A e B para os registros do Quadro 5, bem como da conjunção ¬ A ∧ B.

	Município	Produto		Resultado
	A	B	$\leftarrow A$	$\neg A\wedge B$
1	V	F	F	F
2	V	F	F	F
3	F	V	V	V
4	V	V	F	F
5	F	F	V	F
6	V	F	F	F
7	V	V	F	F
8	F	F	V	F
9	F	V	V	V

Dentro de um algoritmo computacional, o resultado da conjunção, dentro de uma estrutura condicional, pode ser usado para classificar a proposição C, pois se a condição for satisfeita (V) a proposição C também será. Na programação, o operador de implicação é feito por meio do comando se… então…No nosso exemplo podemos dizer se ¬ ∧A B então C, ou seja, em que ¬ ∧A B for V, C também será. Para matar um pouco da nossa vontade de começar a programar, veja no Quadro 6 como ficaria esse comando dentro de três importantes linguagens de programação.

Linguagem	Sintaxe
C	if(A!=”BRASILIA’&&B==”GASOLINA”) { printf(“Petrobras”); }
Java	if(A!=”BRASILIA’&&B==”GASOLINA”) { System.out.println(“Petrobras”); }
Python	if A!=”BRASILIA” and B == “GASOLINA”: print(“Petrobras”)

Quadro 6 | Estrutura condicional em linguagens de programação

Como você pode observar no Quadro 4.18, o comando se é escrito em inglês (if) e o então, nas linguagens C e Java é a chave ( { ) e em python é o dois pontos ( : ). Outro detalhe é a escrita da conjunção; em C e Java é feito pelo && e em python pelo comando and. Além desses conectivos lógicos, também foram usados operadores relacionais. A sintaxe != significa “diferente” e a sintaxe == significa “igual”. Como você pode ver, a solução geral de um problema está na lógica, que não muda de uma linguagem para outra, o que muda é a sintaxe. Por isso, compreender os operadores lógicos é essencial para sua carreira. Não deixe de aprofundar seus estudos e lembre-se: quanto mais você treinar, mais desenvolverá sua lógica e sua capacidade analítica.

Vamos Exercitar?

Chegou o momento de resolvermos mais um desafio. Como funcionário na área de analytics de uma empresa de varejo. Você recebeu uma nova base de dados e precisa identificar os clientes que têm potencial de comprar na nova campanha. A regra para dizer se o cliente tem ou não potencial para comprar é dada pelas seguintes condições:

• Não importa o gênero (pode ser feminino ou masculino).

• Ele ou ela deve ter idade entre 30 e 45 anos.

• Ele ou ela deve ter feito acima de 10 compras.

• Ele ou ela deve ter um ticket médio acima de R$ 50,00. A primeira parte do desafio consiste em escrever uma fórmula que traduza essas regras e, então classificar o resultado da fórmula para cada registro da base da dados.

Primeiro ponto importante para montar a fórmula é entender que todas as condições precisam ser satisfeitas, ou seja, estamos diante de conjunções. Como não importa o gênero – pode ser F ou M –, usaremos a disjunção. Agora é montar essa disjunção com as várias conjunções, utilizando os parênteses para indicar a ordem da valoração. Vamos começar escrevendo os itens já em fórmulas:

• (feminino OU masculino).
• (idade >=30 E idade <=45).
• (compra >= 10). • (ticket médio >= 50).

Agora é só juntar os itens com a conjunção:

(feminino OU masculino) E (idade >=30 E idade <=45) E (compra >= 10) E (ticket médio >= 50). Veja que temos conectores que não são tão evidentes, como no caso da idade, em que precisamos usar a conjunção para delimitar a idade procurada. Agora vamos avaliar a fórmula para os dados. Observe os resultados na coluna “cliente_potencial” na Tabela 3.

Vamos analisar juntos alguns registros. Na linha 1, o gênero, a idade e o valor da última compra são satisfeitos, porém, o total de compras e o ticket médio não são, o que resulta em falso para a coluna que indica se o cliente é ou não potencial. Já na linha 4, todos os itens são atendidos, logo o cliente é classificado como V, ou seja, é um cliente com potencial de compra na campanha.

codigo_ cli	nome_ cli	genero_cli	idade_cli	valor_ compra	total_ compras	Ticket_ medio	cliente_ potencial	cupom_10	cupom_5
53682	Karly Dillon	F	40	74,84	5	45,00	F	?	?
58246	Channing Vazquez	M	49	98,04	20	200,00	F	?	?
27022	Adria Key	F	47	65,93	12	34,00	F	?	?
82075	Ella Nelson	F	34	94,01	16	150,00	V	?	?
90657	Arden Battle	M	48	21,73	4	23,00	F	?	?
80330	Brittany Ramirez	F	38	42,23	1	42,23	F	?	?
53989	Moses Graham	M	42	37,20	29	45,00	F	?	?
61370	Jin Fuller	M	49	65,60	35	123,00	V	?	?
41807	Phelan Blair	M	46	77,40	23	95,00	V	?	?
94269	Porter West	M	22	67,19	6	35,00	F	?	?
56516	Zena Skinner	F	54	73,98	15	60,00	F	?	?
38904	Teagan Rios	M	34	61,57	17	71,00	V	?	?

Tabela 3 | Resultado da valoração da fórmula

Agora que já sabemos quais clientes têm potencial para comprar, vamos ao próximo passo: marcar o cupom de desconto. Devemos escrever uma nova fórmula que traduza “Se o cliente tem potencial de compra, então ele deve ganhar um cupom com 10% de desconto”. Vamos chamar de P a proposição “o cliente tem potencial de compra” e R a proposição “Ganhar um cupom com 10% de desconto”. Então a fórmula pode ser escrita como P → R. Na lógica de programação, a implicação é utilizada em estruturas condicionais do tipo se… então… E como resultado temos que se P for verdadeira então R acontecerá.

Também foi dado a você o desafio de escrever a fórmula que traduza “Se é falso que o cliente tem potencial de compra, então ele deve ganhar um cupom com 5% de desconto”. Considerando a proposição P anterior e a proposição S como “Ganhar um cupom com 5% de desconto”, obtemos a fórmula ¬ P → S. Agora já podemos finalizar o relatório completando as colunas que indicam a qual cupom o cliente tem direito. Veja na Tabela 4 o resultado completo. Vamos analisar a linha 1. Temos que o cliente não é potencial, ou seja, ¬P é uma verdade nesse caso, logo S acontecerá.

codigo_ cli	nome_ cli	genero_cli	idade_cli	valor_ compra	total_ compras	Ticket_ medio	cliente_ potencial	cupom_10	cupom_5
53682	Karly Dillon	F	40	74,84	5	45,00	F	F	V
58246	Channing Vazquez	M	49	98,04	20	200,00	F	F	V
27022	Adria Key	F	47	65,93	12	34,00	F	F	V
82075	Ella Nelson	F	34	94,01	16	150,00	V	V	F
90657	Arden Battle	M	48	21,73	4	23,00	F	F	V
80330	Brittany Ramirez	F	38	42,23	1	42,23	F	F	V
53989	Moses Graham	M	42	37,20	29	45,00	F	F	V
61370	Jin Fuller	M	49	65,60	35	123,00	V	V	F
41807	Phelan Blair	M	46	77,40	23	95,00	V	V	F
94269	Porter West	M	22	67,19	6	35,00	F	F	V
56516	Zena Skinner	F	54	73,98	15	60,00	F	F	V
38904	Teagan Rios	M	34	61,57	17	71,00	V	V	F

Tabela 4 | Relatório final

Com esses resultados finalizamos nosso desafio, contribuindo com êxito com a área de marketing da empresa. Esperamos que venham novos desafios!

Saiba Mais

Aplicações da tabela verdade são fundamentais para a compreensão da disciplina Lógica e Matemática Computacional. A seguir, algumas indicações para um estudo profundo sobre o tema.

1. BISPO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à Lógica Matemática. Cengage Learning Brasil, 2017. O capítulo 2 deste livro aborda os tópicos referentes: (1) à Tabela Verdade, (2) aos Exercícios.
2. QUILELLI, P. Raciocínio lógico matemático para concursos. 3. ed. Editora Saraiva, 2015. O capítulo 2 aborda os tópicos relacionados à tabela verdade.

Referências Bibliográficas

BISPO FILHO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à lógica matemática. São Paulo: Cengage Learning, 2017.

FAJARDO, R. Lógica matemática. 1. ed. São Paulo: Edusp, 2017.

MUNDIM, R. P. A Lógica Formal – princípios elementares. Revista Economia & Gestão, Belo Horizonte, v. 2, n. 3, jan./jun. 2002.

SANTOS, M. da S. dos et al. Lógica computacional. Grupo A, 2021.

Videoaula de Encerramento

Estudante, esta videoaula foi preparada especialmente para você. Nela, você irá aprender conteúdos importantes para a sua formação profissional. Vamos assisti-la? Bons estudos!

Clique aqui para acessar os slides da sua videoaula.

Ponto de Chegada

Olá, estudante! Para desenvolver a competência desta Unidade, que está relacionado à Tabela verdade, você deverá primeiramente conhecer os conceitos fundamentos sobre: Tabela verdade, Lei de Morgan, Disjunção, Negação, conectores (AND e OR), implicação lógica, tautologia, bicondicional e por fim regras de precedência.

Bom, então vamos lá.

Tabela Verdade

A tabela verdade é uma representação sistemática de todas as combinações possíveis de valores de verdade para proposições em uma expressão lógica. Ela demonstra de maneira abrangente os resultados da expressão para todas as situações.

Lei de Morgan

A Lei de Morgan é um princípio fundamental na lógica proposicional que descreve como a negação de uma conjunção (E) é equivalente à disjunção (OU) das negações das proposições individuais, e vice-versa. Em termos simples, é uma regra que relaciona negações e operadores lógicos.

Disjunção

A disjunção é um operador lógico representado por "OU." Em uma expressão disjuntiva, se pelo menos uma das proposições é verdadeira, a expressão como um todo é verdadeira. Caso contrário, a expressão é falsa.

Negação

A negação é um operador lógico representado por "¬" (não). Ele inverte o valor de verdade de uma proposição: se a proposição é verdadeira, a negação torna-se falsa, e vice-versa.

Estas definições fornecem uma visão sucinta dos conceitos de tabela verdade, Lei de Morgan, disjunção e negação na lógica proposicional.

Conector "AND" (E)

O conector "AND" é um operador lógico que denota a conjunção de duas proposições. Em uma expressão

A ∧ B, a sentença é verdadeira apenas se ambas as proposições A e B forem verdadeiras.

Conector "OR" (OU)

O conector "OR" é um operador lógico que denota a disjunção de duas proposições. Em uma expressão A ∨ B, a sentença é verdadeira se pelo menos uma das proposições A ou B for verdadeira.

Negação ("NOT")

A negação é um operador lógico unário que inverte o valor de verdade de uma proposição. Em uma expressão ¬A, se A é verdadeiro, a negação é falsa, e vice-versa.

Negação "AND" ("NOT AND")

A negação "AND" é uma combinação da negação e do conector "AND". Em uma expressão ¬(A ∧ B), a sentença é verdadeira quando pelo menos uma das proposições A ou B for falsa.

Negação "OR" ("NOT OR")

A negação "OR" é uma combinação da negação e do conector "OR". Em uma expressão ¬(A ∨ B), a sentença é verdadeira apenas quando ambas as proposições A e B são falsas.

Implicação Lógica

A implicação lógica, representada por "A → B", indica que se a proposição A for verdadeira, então a proposição B também o é. Se A for falsa, a implicação é automaticamente verdadeira. Apenas quando A é verdadeira e B é falsa é que a implicação é falsa. Essa estrutura condicional é fundamental em lógica matemática e raciocínio condicional.

Tabela verdade para condicional

A tabela verdade para a condicional (implicação) "A → B" revela que, se A for verdadeiro e B for verdadeiro, a condicional é verdadeira. Se A for verdadeiro e B for falso, a condicional é falsa. Quando A é falso, a condicional é sempre verdadeira, independentemente de B. Essa tabela esquematiza as relações lógicas entre A e B em contextos condicionais.

Tautologia

Uma tautologia é uma proposição lógica sempre verdadeira, independentemente dos valores de verdade das variáveis envolvidas. Em uma tabela verdade, todas as linhas apresentam resultado "verdadeiro". Exemplo: "A ou não A" é uma tautologia, pois a afirmação "A ou não A" é verdadeira em todas as situações, já que A ou não A sempre é verdadeiro. Tautologias são fundamentais na lógica matemática e têm aplicações em raciocínio lógico e teoria dos conjuntos.

Bicondicional

O operador bicondicional, representado por "A ↔ B", é uma afirmação lógica que é verdadeira quando ambas as proposições A e B têm o mesmo valor de verdade, seja verdadeira ou falsa. Em uma tabela verdade para o bicondicional, as únicas situações em que a expressão é verdadeira são quando A e B têm ambos os valores verdadeiros ou ambos os valores falsos. Se há uma disparidade nos valores de verdade entre A e B, o bicondicional é falso. Em resumo, o bicondicional expressa a equivalência lógica entre duas proposições.

Regras de Precedência

As regras de precedência em lógica estabelecem a ordem de avaliação dos operadores lógicos em expressões. Geralmente, a negação (¬) tem a mais alta precedência, seguida pela conjunção (∧), disjunção (∨), condicional (→), e bicondicional (↔). Parênteses podem ser usados para alterar a ordem padrão de avaliação.

É Hora de Praticar!

Suponha que uma empresa de TI está conduzindo um teste para avaliar a qualificação dos candidatos. Eles têm dois critérios principais: habilidades de programação (A) e habilidades de comunicação (B). A empresa decidiu que um candidato é qualificado (Q) se tiver habilidades de programação e boas habilidades de comunicação, ou se não tiver habilidades de programação, mas ainda tiver habilidades de comunicação.

Definição das Variáveis:

• A: Habilidades de programação.
• B: Habilidades de comunicação.
• Q: Qualificação

A expressão lógica para a qualificação (Q) pode ser escrita como:

Q = (A ∧ B) ∨ (¬A ∧ B)

Análise da Expressão Lógica:

• (A ∧ B): Representa a condição em que um candidato possui habilidades tanto em programação quanto em comunicação.
• (¬A ∧ B): Representa a condição em que um candidato não possui habilidades de programação (¬A), mas possui habilidades de comunicação.
• (A ∧ B) ∨ (¬A ∧ B): Representa a condição geral de qualificação, em que um candidato será qualificado se atender a uma das condições acima.

Com base no que foi exposto, como podemos expressar essa condição usando uma expressão lógica? Além disso, qual seria o resultado dessa expressão para diferentes combinações de habilidades de programação e comunicação?"

Reflita

• Como a ordem de precedência dos operadores lógicos (¬, ∧, ∨) afeta a avaliação de expressões? Cite exemplos de como o uso de parênteses muda essa ordem e influencia o resultado?
• O que é uma tautologia em lógica? Cite exemplos práticos?
• O que caracteriza uma tautologia em lógica proposicional? Além disso, como o operador bicondicional (↔) opera na relação entre duas proposições, e qual é a sua representação em termos de tabela verdade?

Resolução do estudo de caso

O teste de qualificação, baseado nessa lógica, destina-se a identificar candidatos que possuam habilidades em programação e/ou comunicação, refletindo os critérios específicos da empresa de TI para a posição em questão. O entendimento da expressão lógica e a interpretação da tabela verdade são essenciais para analisar a adequação dos candidatos à empresa.

Neste contexto, temos a seguinte expressão Lógica para Qualificação:

Q= (A ∧ B) ∨ (¬A ∧ B)

Para resolver esta expressão, dividiremos o processo em três etapas. Para cada uma delas, será elaborada uma Tabela Verdade para melhor ilustração.

• Etapa 1: Tabela verdade para (A ∧ B):

A	B	$(A\wedge B)$
V V F F	V F V F	V F F F

• Etapa 2: Tabela verdade para (¬A ∧ B):

A	B	$\neg A$	$(\neg A\wedge B)$
V V F F	V F V F	F F V V	F F V F

• Etapa 3: Tabela verdade para (A ∧ B) ∨ (¬A ∧ B):

A	B	$(A\wedge B)$	$(\neg A\wedge B)$	$(A\wedge B)\vee (\neg A\wedge B)$
V V F F	V F V F	V F F F	F F V F	V F V F

Por fim, este exemplo prático ilustra como a lógica, a tabela verdade e a interpretação são aplicadas em um contexto de teste para seleção de candidatos em uma empresa de TI, levando em consideração diferentes combinações de habilidades.

Dê o play!

Assimile

Referências

BISPO FILHO, C. A. F.; CASTANHEIRA, L. B.; SOUZA FILHO, O. M. Introdução à lógica matemática. São Paulo: Cengage Learning, 2017.

FAJARDO, R. Lógica matemática. 1. ed. São Paulo: Edusp, 2017.

MUNDIM, R. P. A Lógica Formal – princípios elementares. Revista Economia & Gestão, Belo Horizonte, v. 2, n. 3, jan./jun. 2002.

SANTOS, M. da S. dos et al. Lógica computacional. Grupo A, 2021.